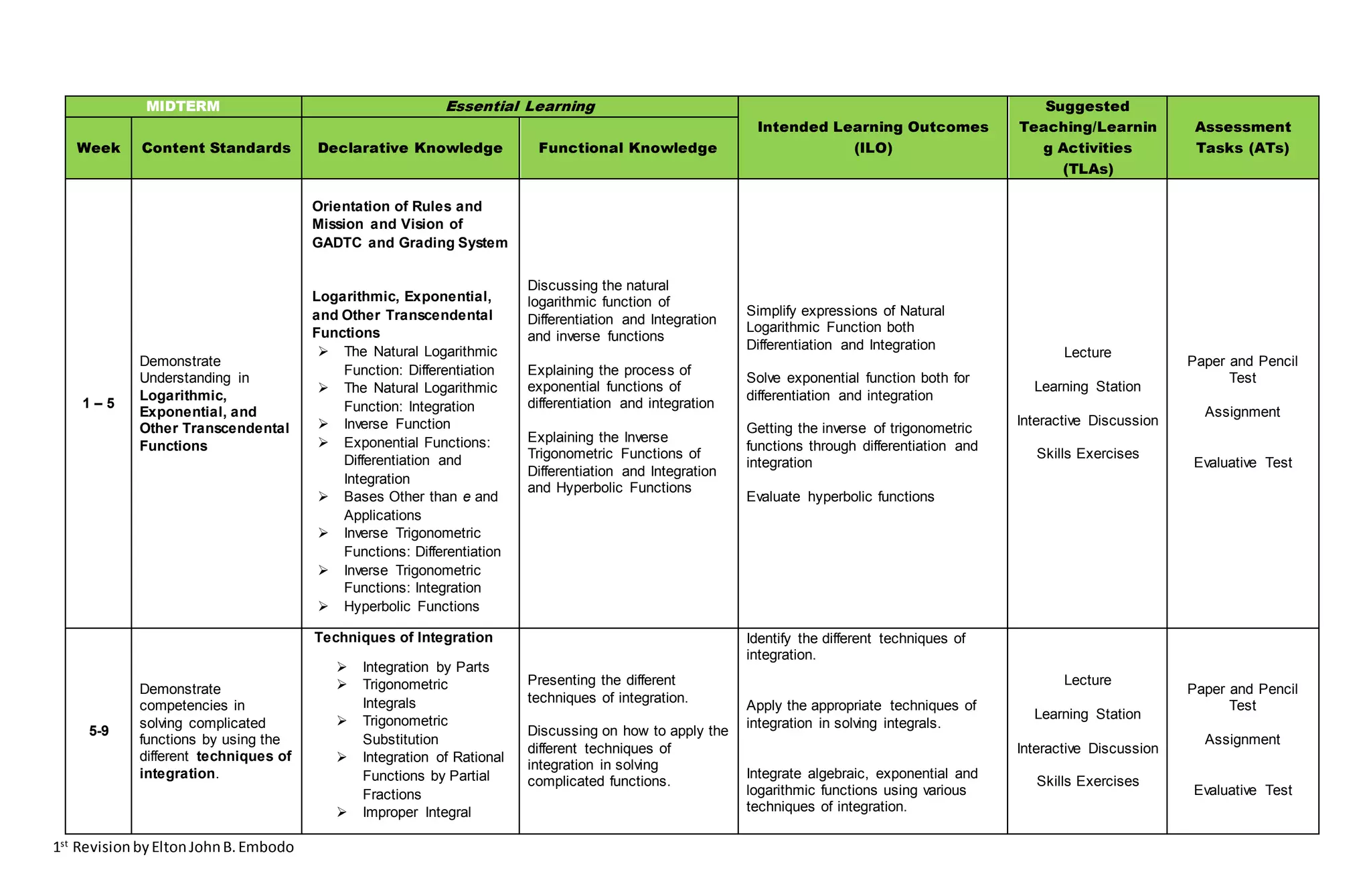
1. This document outlines the teaching and learning plan for a Calculus 2 course, including course description, intended learning outcomes at the institute, program, and course level, as well as content, activities, and assessments for each topic covered over the semester. 2. The course aims to further develop students' understanding of differential and integral calculus, covering integration methods and techniques, indeterminate forms, and improper integrals of various functions. 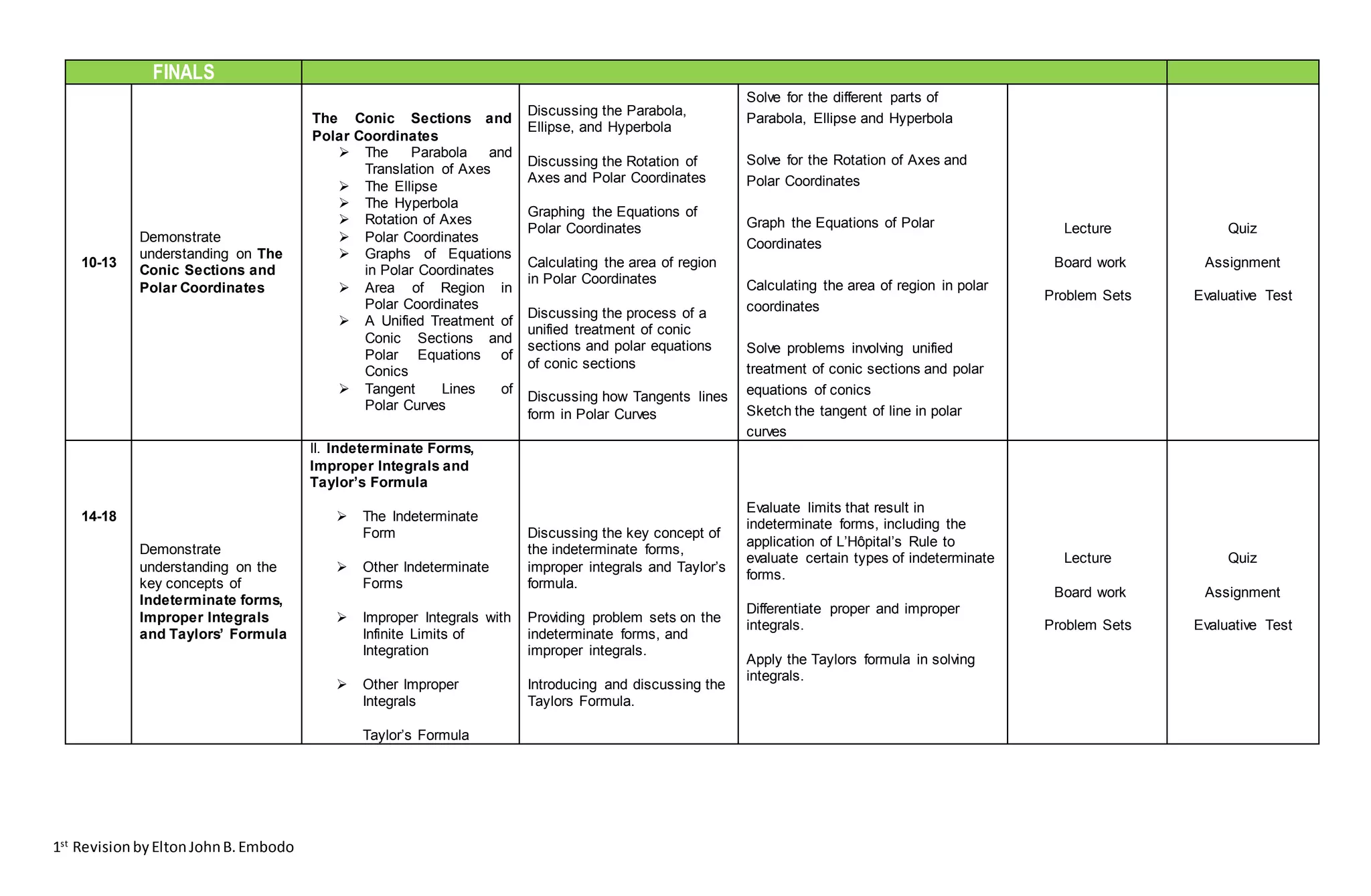3. Over the semester, students will learn about logarithmic, exponential, and other transcendental functions; various integration techniques; conic sections and polar coordinates; indeterminate forms, improper integrals; and Taylor's formula through lectures, exercises, assignments and evaluations.

1. 1st
RevisionbyEltonJohnB.Embodo
GOV. ALFONSO D. TAN COLLEGE
Bachelor of Secondary Education major in Mathematics (BSEd-Math)
Outcomes – Based Teaching and Learning Plan in ME 110
Alfonsos as Lux Mundi: Serving Humanity with Empowered Mind, Passionate Heart and Virtuous Soul
Course Title Calculus 2 Course Code ME 110
Credit Units 4 Course Pre-/Co-requisites Calculus 1 with Analytic Geometry
Course Description
(CMO 75 s. 2017)
This course aims to further develop the students’ understanding of differential and integral calculus. It covers topics on the methods and
techniques of integration, indeterminate form, and improper integrals of algebraic and transcendental functions.
Institute Intended
Learning Outcomes
(IILO)
Graduates of BSEd programs are teachers who:
a. Articulate the rootedness of education in philosophical, socio-cultural, historical, psychological, and political contexts
b. Demonstrate mastery of subject matter/discipline
c. Facilitate learning using a wide range of teaching methodologies and delivery modes appropriate to specific learners and their
environment
d. Develop innovative curricula, instructional plans, teaching approaches, and resources for diverse learners
e. Apply skills in the development and utilization of ICT to promote quality, relevant, and sustainable educational practices
f. Demonstrate a variety of thinking skills in planning, monitoring, assessing, and reporting learning processes and outcomes
g. Practice professional and ethical teaching standards sensitive to the local, national, and global realities
h. Pursue lifelong learning for personal and professional growth through varied experiential and field-based opportunities
Program Intended
Learning Outcomes
(PILO)
At the end of this program, graduates will have the ability to:
a. Exhibit competence in mathematical concepts and procedures.
b. Exhibit proficiency in relating mathematics to other curricular areas.
c. Manifest meaningful and comprehensive pedagogical content knowledge (PCK) of mathematics.
d. Demonstrate competence in designing, constructing and utilizing different forms of assessment in mathematics.
e. Demonstrate proficiency in problem-solving by solving and creating routine and non-routine problems with different levels of
complexity.
f. Use effectively appropriate approaches, methods, and techniques in teaching mathematics including technological tools.
g. Appreciate mathematics as an opportunity for creative work, moments of enlightenment, discovery and gaining insights of the world.
Course Intended
Learning Outcomes
(CILO)
At the end of this course, the students should be able to:
a. Demonstrate ability to integrate more complicated functions using the standard methods of integration, including integration by parts, trigonometric
integrals, trigonometric substitution and partial fractions.
b. Describe curves parametrically and apply Calculus concepts and techniques to curves.
c. Express curves via polar equations and to solve Calculus problems in the polar coordinate system.
d. Represent vectors analytically and geometrically, and compute dot and cross products of lines and planes
e. Solve application problems.

2. 1st
RevisionbyEltonJohnB.Embodo
MIDTERM Essential Learning
Intended Learning Outcomes
(ILO)
Suggested
Teaching/Learnin
g Activities
(TLAs)
Assessment
Tasks (ATs)Week Content Standards Declarative Knowledge Functional Knowledge
1 – 5
Demonstrate
Understanding in
Logarithmic,
Exponential, and
Other Transcendental
Functions
Orientation of Rules and
Mission and Vision of
GADTC and Grading System
Logarithmic, Exponential,
and Other Transcendental
Functions
 The Natural Logarithmic
Function: Differentiation
 The Natural Logarithmic
Function: Integration
 Inverse Function
 Exponential Functions:
Differentiation and
Integration
 Bases Other than e and
Applications
 Inverse Trigonometric
Functions: Differentiation
 Inverse Trigonometric
Functions: Integration
 Hyperbolic Functions
Discussing the natural
logarithmic function of
Differentiation and Integration
and inverse functions
Explaining the process of
exponential functions of
differentiation and integration
Explaining the Inverse
Trigonometric Functions of
Differentiation and Integration
and Hyperbolic Functions
Simplify expressions of Natural
Logarithmic Function both
Differentiation and Integration
Solve exponential function both for
differentiation and integration
Getting the inverse of trigonometric
functions through differentiation and
integration
Evaluate hyperbolic functions
Lecture
Learning Station
Interactive Discussion
Skills Exercises
Paper and Pencil
Test
Assignment
Evaluative Test
5-9
Demonstrate
competencies in
solving complicated
functions by using the
different techniques of
integration.
Techniques of Integration
 Integration by Parts
 Trigonometric
Integrals
 Trigonometric
Substitution
 Integration of Rational
Functions by Partial
Fractions
 Improper Integral
Presenting the different
techniques of integration.
Discussing on how to apply the
different techniques of
integration in solving
complicated functions.
Identify the different techniques of
integration.
Apply the appropriate techniques of
integration in solving integrals.
Integrate algebraic, exponential and
logarithmic functions using various
techniques of integration.
Lecture
Learning Station
Interactive Discussion
Skills Exercises
Paper and Pencil
Test
Assignment
Evaluative Test

3. 1st
RevisionbyEltonJohnB.Embodo
FINALS
10-13
Demonstrate
understanding on The
Conic Sections and
Polar Coordinates
The Conic Sections and
Polar Coordinates
 The Parabola and
Translation of Axes
 The Ellipse
 The Hyperbola
 Rotation of Axes
 Polar Coordinates
 Graphs of Equations
in Polar Coordinates
 Area of Region in
Polar Coordinates
 A Unified Treatment of
Conic Sections and
Polar Equations of
Conics
 Tangent Lines of
Polar Curves
Discussing the Parabola,
Ellipse, and Hyperbola
Discussing the Rotation of
Axes and Polar Coordinates
Graphing the Equations of
Polar Coordinates
Calculating the area of region
in Polar Coordinates
Discussing the process of a
unified treatment of conic
sections and polar equations
of conic sections
Discussing how Tangents lines
form in Polar Curves
Solve for the different parts of
Parabola, Ellipse and Hyperbola
Solve for the Rotation of Axes and
Polar Coordinates
Graph the Equations of Polar
Coordinates
Calculating the area of region in polar
coordinates
Solve problems involving unified
treatment of conic sections and polar
equations of conics
Sketch the tangent of line in polar
curves
Lecture
Board work
Problem Sets
Quiz
Assignment
Evaluative Test
14-18
Demonstrate
understanding on the
key concepts of
Indeterminate forms,
Improper Integrals
and Taylors’ Formula
II. Indeterminate Forms,
Improper Integrals and
Taylor’s Formula
 The Indeterminate
Form
 Other Indeterminate
Forms
 Improper Integrals with
Infinite Limits of
Integration
 Other Improper
Integrals
Taylor’s Formula
Discussing the key concept of
the indeterminate forms,
improper integrals and Taylor’s
formula.
Providing problem sets on the
indeterminate forms, and
improper integrals.
Introducing and discussing the
Taylors Formula.
Evaluate limits that result in
indeterminate forms, including the
application of L’Hôpital’s Rule to
evaluate certain types of indeterminate
forms.
Differentiate proper and improper
integrals.
Apply the Taylors formula in solving
integrals.
Lecture
Board work
Problem Sets
Quiz
Assignment
Evaluative Test

4. 1st
RevisionbyEltonJohnB.Embodo
Basic Readings The Calculus with Analytic Geometry Sixth Edition
 Louis Leithold
Calculus
 Ron Larson
 Bruce H. Edwards
Extended Readings
Course Assessment As identifiedin the Assessment Task
Course Policies LanguageofInstructions
English
Attendance
 As identifiedin the student handbook
Homework,Quizzes,Written Reports,ReactionPapersand Portfolio
Special Requirement
GradingSystem
Summative Quizzes - 30%
SummativePerformance - 40%
Periodical Exam - 30%
100%
Classroom RulesandRegulations
 Respect
Committee Members CommitteeLeader : Alemar C. Mayordo
Members : Elton John B. Embodo
ZarleneM.Tigol
RogielouP. Andam
Clint Joy Quije
Consultation Schedule FacultyMember : ZarleneM.Tigol
ContactNumber : 09503350862
E-mailaddress : zarlenetigol@yahoo.com
ConsultationHours:
TimeandVenue :
Course
Title
A.Y. Term of
Effectivity
Prepared by Checked by Noted by Approved by Pages
CALCULUS
2 2019-2020 ZARLENE M. TIGOL
Instructor
ELTONJOHNB.EMBODO,MAED
Program Coordinator
ALEMAR C. MAYORDO, MAED
OIC-Dean
LOVE H. FALLORAN, Ph.D
VP for Academics
4

5. 1st
RevisionbyEltonJohnB.Embodo