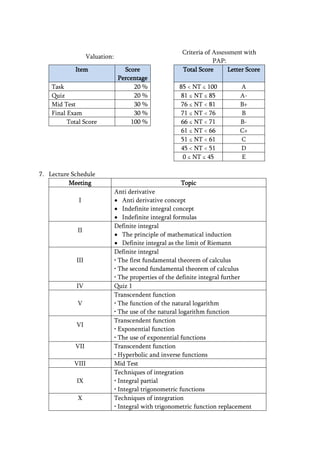
This document provides a summary of the Calculus II course including: 1) The course covers concepts of anti-derivatives, definite integrals, transcendental functions, and integration techniques. 2) The course objectives are for students to understand integral concepts and solve problems logically. 3) Student assessment is based on assignments, quizzes, midterms, and a final exam, with grades ranging from A to E.

1. LECTURES CONTRACT
Course
Course Code
Semester
Date/Time
Class
Course Status
: Calulus II
: KPC 9208
: II
: Tuesday/07.30 - 10.00 AM
: F8
: Compulsory
1. Course Description
Calculus II is an integral basic courses that discuss a variety of functions concepts,
theorems, and algorithms are intuitive and not too formal, and their application in various
problems. The topics studied in this course is the anti derivative, the definite integral,
transcendental functions, techniques of integration, indeterminate forms and improper
integrals, and the use of the definite integral.
2. Course Objectives
Students understand some concepts and theorems of integral functions and can think
logically in solving the existing problems.
3. Learning Method
o Lectures
o Discussion
o Presentation
oQ&A
o Work assignments, quizzes, midterms and final exams
4. Material / Reading Material
• Martono, K. (1999). Calculus. Jakarta: Erlangga.
• Mursita, D. (2006). Basic Mathematics for College. Jakarta: Rekayasa Sains.
• Purcell, E. J. and Varberg, D. (1987). Calculus and Analytical Geometry Volume I.
(Fifth Edition). Jakarta: Erlangga.
• Steward Stewart, J. (2001). Calculus Volume 1. Fourth Edition. Jakarta: Erlangga.
• Basic Math TPB. (1997). Basic Math I. Pekanbaru: TPB Matdas University of Riau.
5. The task for students
The task given to the students divided into two groups of tasks and individual tasks. The
task group in the form of the distribution of material by lecturers to be presented by each
group in several meetings and the problems to be solved in groups. Each group consists
of 6-7 people. While the individual tasks in the form of questions given in the form of a
series of meetings and homework.
6. Criteria for assessment of student learning outcomes
Student learning outcomes assessment is done by giving assignments, quizzes, and exams
are determined by the weight of assessment of students and lecturers. Students are
considered successful if it had received at least C.

2. Valuation:
Item
Task
Quiz
Mid Test
Final Exam
Total Score
7. Lecture Schedule
Meeting
I
II
III
IV
V
VI
VII
VIII
IX
X
Score
Percentage
20 %
20 %
30 %
30 %
100 %
Criteria of Assessment with
PAP:
Total Score
Letter Score
85 < NT ≤ 100
81 ≤ NT ≤ 85
76 ≤ NT < 81
71 ≤ NT < 76
66 ≤ NT < 71
61 ≤ NT < 66
51 ≤ NT < 61
45 < NT < 51
0 ≤ NT ≤ 45
A
AB+
B
BC+
C
D
E
Topic
Anti derivative
Anti derivative concept
Indefinite integral concept
Indefinite integral formulas
Definite integral
The principle of mathematical induction
Definite integral as the limit of Riemann
Definite integral
• The first fundamental theorem of calculus
• The second fundamental theorem of calculus
• The properties of the definite integral further
Quiz 1
Transcendent function
• The function of the natural logarithm
• The use of the natural logarithm function
Transcendent function
• Exponential function
• The use of exponential functions
Transcendent function
• Hyperbolic and inverse functions
Mid Test
Techniques of integration
• Integral partial
• Integral trigonometric functions
Techniques of integration
• Integral with trigonometric function replacement

3. XI
XII
XIII
XIV
XV
XVI
XVII
XVIII
Techniques of integration
• Integral rational function
Indeterminate form and improper integrals
• Indeterminate Forms
• Improper integrals
Quiz 2
The use of the definite integral
• The total area
The use of the definite integral
• Content (volume) objects rotate
The use of the definite integral
• The center of mass
Sequences and series
• Rows
• Monotonous and limited rows
• Infinite series with constant terms
• Infinite series with positive terms
Final Exam
Pekanbaru, February 2013
Lecturer,
Team Teaching