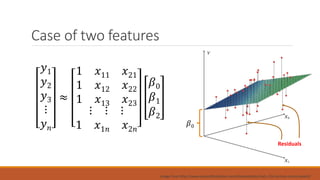
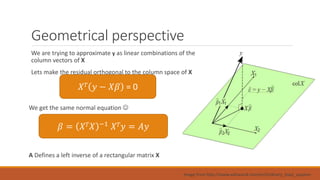
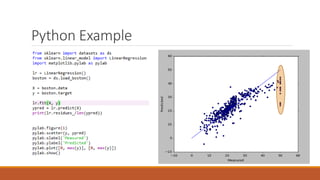
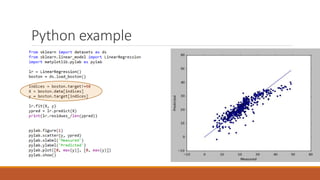
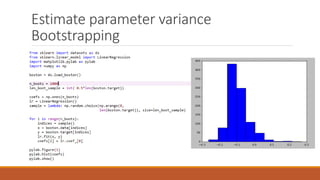
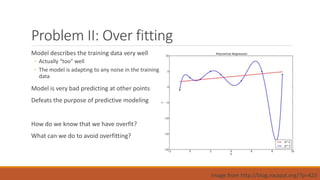
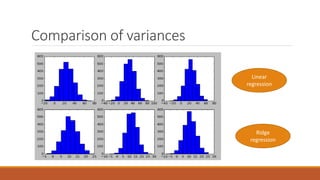
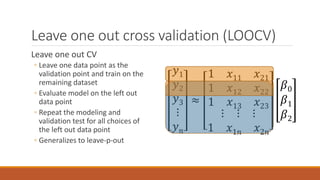
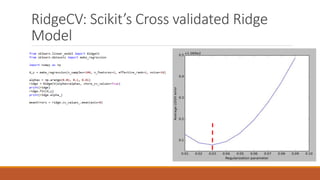
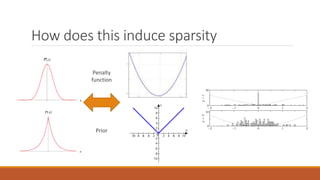
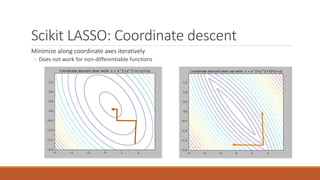
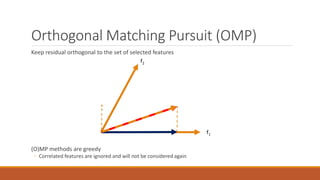
Linear regression models a quantity as a linear combination of features to minimize residuals. Issues include unstable results from collinear features and overfitting. Regularization like ridge regression addresses this by minimizing residuals and coefficient size, improving variance. Cross-validation chooses the best model by evaluating prediction error on validation data rather than training error. Lasso induces sparsity by minimizing residuals and the L1 norm of coefficients. Scikit Learn implements these methods with options like normalization, intercept fitting, and solver choices.