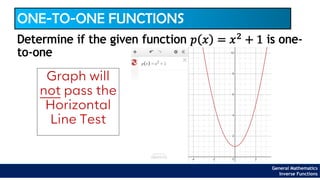
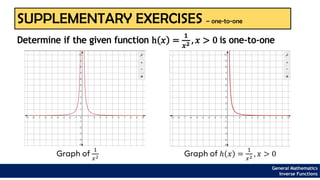
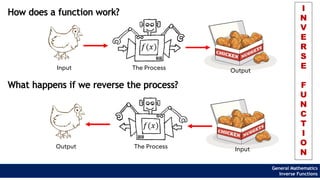
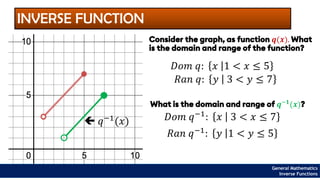
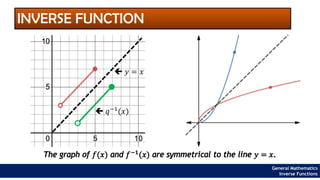
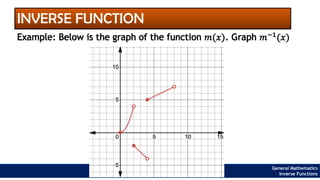
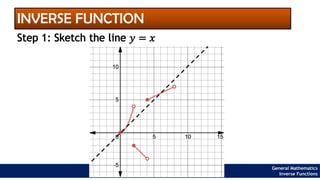
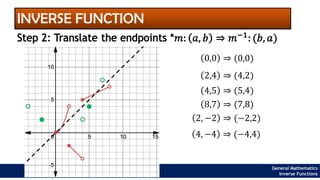
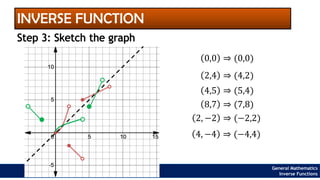
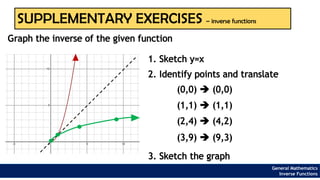
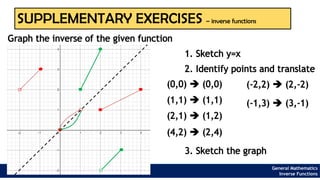
The document provides an overview of inverse functions in mathematics, particularly focusing on one-to-one functions and the criteria for distinguishing them. It explains the concepts of unique mapping, the horizontal line test, and the relationship between a function and its inverse, including the conditions under which an inverse exists. Additionally, supplementary exercises are included to reinforce the understanding of these concepts and verify if functions are inverses of each other.

1. Inverse
Functions
University of Santo Tomas
Senior High School
GENERAL MATHEMATICS

2. RECALL
What is a function?
a. Type of relations
b. Mapping of elements in the domain to a
unique element in another set called range
c. Mapping can be one-to-one or many-to-one
d. The graph passes the VERTICAL LINE TEST
*Remark: {(1,2), (3,2), (4,2)} is considered a function (many-to-one) where each
ordered pair is uniquely mapped but not distinct.

3. Overview
In this lesson, we will:
a. Define one-to-one functions
b. Identify/verify one-to-one functions
c. Define inverse functions
d. Verify if functions are inverses
e. Identify the inverse of a function
General Mathematics
Inverse Functions

4. ONE-TO-ONE FUNCTIONS
•Elements in the domain should correspond to
exactly one element in the range. Ordered pairs
should be unique and distinct from each other.
• A function 𝑓 is one-to-one if for every value 𝑎, 𝑏 in
𝑑𝑜𝑚 𝑓 such that if 𝒂 ≠ 𝒃, then 𝒇(𝒂) ≠ 𝒇(𝒃); or
otherwise, if 𝑓(𝑎) = 𝑓(𝑏), then 𝑎 = 𝑏.
General Mathematics
Inverse Functions

5. ONE-TO-ONE FUNCTIONS
•Both are functions
•S is one-to-one (unique mapping with distinct elements)
•R is a function but not one-to-one (unique mapping
but not distinct elements)
𝑆 = 1,2 , 3,4 , 5,6 ; 𝑅 = {(−2,6), (8,2), (6, −3), (−1,6)}
*Remark: (a) function means no repetition in the elements of the domain
(b) one-to-one means no repetition of elements in both the domain and the range.

6. ONE-TO-ONE FUNCTIONS
•Elements in the domain should correspond to
exactly one element in the range. Ordered pairs
should be unique and distinct from each other.
• A function 𝑓 is one-to-one if for every value 𝑎, 𝑏 in
𝑑𝑜𝑚 𝑓 such that if 𝒂 ≠ 𝒃, then 𝒇(𝒂) ≠ 𝒇(𝒃); or
otherwise, if 𝑓(𝑎) = 𝑓(𝑏), then 𝑎 = 𝑏.
•Graph passes the HORIZONTAL LINE TEST
General Mathematics
Inverse Functions

7. ONE-TO-ONE FUNCTIONS
If every horizontal line intersects the graph of a
function in at most one point, then the function
is one-to-one.
Horizontal Line Test Theorem
Not one-to-one ONE-TO-ONE Not One-to-one, Not a function

8. ONE-TO-ONE FUNCTIONS
Test for Functions Test for One-to-One Functions
No repetition in the domain, values
of abscissa.
No repetition for both the domain
and range. Values of the abscissa
and ordinate are all uniquely and
distinctly mapped.
One-to-one mapping
Many-to-one mapping
One-to-one mapping
Graph must pass the VERTICAL LINE
TEST
Graph must pass the HORIZONTAL
LINE TEST
General Mathematics
Inverse Functions

9. General Mathematics
Inverse Functions
ONE-TO-ONE FUNCTIONS
•algebraically., we follow the two
conditions in the definition to prove:
- Assume values 𝑎 and 𝑏 from Domain.
- let 𝑓(𝑎) = 𝑓(𝑏), then 𝑎 should be equal to 𝑏.
- Otherwise it is not one-to-one.
Determine if the given function 𝒑 𝒙 = 𝒙𝟐
+ 𝟏 is one-
to-one

10. ONE-TO-ONE FUNCTIONS
Let a and b be elements in the domain
Determine if the given function 𝒑 𝒙 = 𝒙𝟐
+ 𝟏 is one-
to-one
Assume 𝑝 𝑎 = 𝑝(𝑏)
𝑎2
+ 1 = 𝑏2
+ 1
𝑎2
= 𝑏2
𝑎2 = 𝑏2
General Mathematics
Inverse Functions
±𝑎 = ±𝑏
Notice that 𝑎 =
𝑏, −𝑏
similarly, 𝑏 = 𝑎, −𝑎
a and b are not
unique and not
even equal.
The test failed. p(x)
is NOT one-to-one

11. ONE-TO-ONE FUNCTIONS
Find a value for a and b that will yield the same
value for 𝑝(𝑥) to prove it is not one-to-one
Determine if the given function 𝑝 𝑥 = 𝑥2
+ 1 is one-
to-one
If 𝑎 = 2, and 𝑏 = −2
p −2 = −2 2
+ 1
= 5
p 2 = 2 2
+ 1
= 5
*Remark: (a) one-to-one means f(a) will only be equal to f(b) if a and b are equal

12. General Mathematics
Inverse Functions
ONE-TO-ONE FUNCTIONS
Graph will
not pass the
Horizontal
Line Test
Determine if the given function 𝑝 𝑥 = 𝑥2
+ 1 is one-
to-one

13. General Mathematics
Inverse Functions
ONE-TO-ONE FUNCTIONS
Let a and b be elements in the domain
Determine if the given function 𝑞 𝑥 = 2 𝑥 + 1 is one-
to-one
Assume 𝑞 𝑎 = 𝑞(𝑏)
2|𝑎 + 1| = 2|𝑏 + 1|
|𝑎 + 1| = |𝑏 + 1|
𝑎 + 1 = 𝑏 + 1 or a + 1 = −(b + 1)
𝑎 = 𝑏 or a = −b − 2 Not one-to-one
𝑎 = 𝑏 + 1 − 1 or a = −b − 1 − 1

14. ONE-TO-ONE FUNCTIONS
Trial and error, we find x=3 and x=-5 will yield the
same value for q(x)
Determine if the given function q 𝑥 = 2 𝑥 + 1 is one-
to-one
= 8
𝑞(3) = 2|3 + 1|
= 8
𝑞(−5) = 2| − 5 + 1|
Not one-to-one
*still a function
General Mathematics
Inverse Functions
Technique: Graph and use Horizontal Line Test

15. ONE-TO-ONE FUNCTIONS
Let a and b be elements in the domain
Determine if the given function r 𝑥 =
1
𝑥
is one-to-one
Assume 𝑟 𝑎 = 𝑟(𝑏)
1
𝑎
=
1
𝑏
𝑎 = 𝑏
Function is
ONE-TO-ONE
General Mathematics
Inverse Functions
Technique: Graph and use Horizontal Line Test

16. General Mathematics
Inverse Functions
SUPPLEMENTARY EXERCISES – one-to-one
Let a, b be elements in the domain
Determine if the given function 𝑝 𝑥 =
3𝑥−2
2
is one-to-one
Assume 𝒑 𝒂 = 𝒑 𝒃
𝟑 𝒂 − 𝟐
𝟐
=
𝟑 𝒃 − 𝟐
𝟐
𝟑𝒂 − 𝟐 = 𝟑𝒃 − 𝟐
𝟑𝒂 = 𝟑𝒃
𝒂 = 𝒃
∴ 𝒑 𝒙 𝒊𝒔 𝒐𝒏𝒆 − 𝒕𝒐 − 𝒐𝒏𝒆

17. General Mathematics
Inverse Functions
SUPPLEMENTARY EXERCISES – one-to-one
Let a, b be elements in the domain
Determine if the given function g 𝑥 = 𝑥3
is one-to-one
A𝒔𝒔𝒖𝒎𝒆 𝒈 𝒂 = 𝒈 𝒃
𝒂𝟑 = 𝒃𝟑
𝟑
𝒂𝟑 =
𝟑
𝒃𝟑
𝒂 = 𝒃
∴ 𝒈 𝒙 𝒊𝒔 𝒐𝒏𝒆 − 𝒕𝒐 − 𝒐𝒏𝒆
𝑖𝑓 𝑎 = 2 𝑎𝑛𝑑 𝑏 = −2
𝑔 2 = 8
𝑔 −2 = −8
𝑎 ≠ 𝑏 ⇒ 𝑔 𝑎 ≠ 𝑔 𝑏

18. SUPPLEMENTARY EXERCISES– one-to-one
Let a, b be elements in the domain
Determine if the given function 𝑐 𝑥 = 𝑥3 − 2𝑥2 − 15𝑥 is one-to-one
A𝒔𝒔𝒖𝒎𝒆 𝒄 𝒂 = 𝒄 𝒃
𝒂𝟑 − 𝟐𝒂𝟐 − 𝟏𝟓𝒂 = 𝒃𝟑 − 𝟐𝒃𝟐 − 𝟏𝟓𝒃
𝒂(𝒂𝟐 − 𝟐𝒂 − 𝟏𝟓) = 𝒃 𝒃𝟐 − 𝟐𝒃 − 𝟏𝟓
𝒂 𝒂𝟐
− 𝟐𝒂 − 𝟏𝟓 = 𝟎
𝒂 𝒂 + 𝟑 (𝒂 − 𝟓) = 𝟎
𝒂 = 𝟎
𝒂 = −𝟑
𝒂 = 𝟓
General Mathematics
Inverse Functions
𝑎 alone yields 3 values that is
mapped to one value of the
range. ∴ NOT one-to-one
Verify using Horizontal Line Test

19. SUPPLEMENTARY EXERCISES – one-to-one
Let a, b be elements in the domain
Determine if the given function h 𝑥 =
1
𝑥2 , 𝑥 > 0 is one-to-one
A𝒔𝒔𝒖𝒎𝒆 𝒉 𝒂 = 𝒉 𝒃
𝟏
𝒂𝟐
=
𝟏
𝒃𝟐
𝒂𝟐 = 𝒃𝟐
±𝒂 = ±𝒃
∴ NOT one-to-one?
Note however:
The domain limits 𝑥 > 0
+𝑎 = +𝑏
The function is really
one-to-one
General Mathematics
Inverse Functions
Functions which are not one to one
can be restricted in the domain to be
one to one.

20. SUPPLEMENTARY EXERCISES – one-to-one
Determine if the given function h 𝑥 =
1
𝑥2 , 𝑥 > 0 is one-to-one
General Mathematics
Inverse Functions
Graph of
1
𝑥2 Graph of ℎ 𝑥 =
1
𝑥2 , 𝑥 > 0

21. How does a function work?
General Mathematics
Inverse Functions
𝑓(𝑥)
Input The Process Output
What happens if we reverse the process?
𝑓(𝑥)
Output The Process Input
I
N
V
E
R
S
E
F
U
N
C
T
I
O
N

22. INVERSE FUNCTION
If 𝑓 is a one-to-one function defined by the
set of ordered pairs (𝑥, 𝑦), then there exists a
function 𝑓−1, called the inverse function of 𝒇,
where 𝑓−1
is the set of ordered pair (𝑦, 𝑥),
and is defined by
𝒙 = 𝒇−𝟏
(𝒚) if and only if 𝒚 = 𝒇(𝒙)
Note that −1 in 𝑓−1 is not an exponent of f.
General Mathematics
Inverse Functions

23. INVERSE FUNCTION
Theorem: A function 𝑓 has an inverse function if
and only if the function is one-to-one.
Existence of an Inverse Function
Given 𝑓 𝑥 = 2𝑥 + 1 and 𝑔 𝑥 =
𝑥−1
2
𝑓 3 = 7 𝑔 7 = 𝑔(𝑓 3 )
𝑔 7 =
7−1
2
= 3
𝑓 2 = 5 𝑔 5 =
5−1
2
= 2 𝑔 5 = 𝑔(𝑓 2 )
Notice that g reverses the process back to f
General Mathematics
Inverse Functions

24. INVERSE FUNCTION
Given that 𝑔 is an inverse of 𝑓, and
𝑓 1 = 5
what is 𝑔 5 ?
, 𝑓 8 = −10
𝑓 1 = 5 INVERSE 𝑔 5 = 1 = 𝑔(𝑓 1 )
Input
Output Input Output
what is 𝑔 −10 ?
𝑔 −10 = 𝑔 𝑓 8 = 8
General Mathematics
Inverse Functions

25. INVERSE FUNCTION
𝑓 = { 1,3 , (2,6), (3,9), (4,12)}
𝑔 = { 2,3 , 9, −6 , 13,2 , (3,4)}
ℎ = 9,4 , −8, −8 , 3,6 , 15,1
𝑣 = { 1,1 , 2,2 , 4,1 , (5,2)}
Observe the elements of each function and their inverses
𝑓−1
= { 3,1 , (6,2), (9,3), (12,4)}
𝑔−1 = { 3,2 , −6,9 , 2,13 , (4,3)}
ℎ−1 = 4,9 , −8, −8 , 6,3 , 1,15
𝑣−1 = { 1,1 , 2,2 , 1,4 , (2,5)}
𝑥, 𝑦 𝑖𝑛 𝑓 𝑏𝑒𝑐𝑜𝑚𝑒𝑠 𝑦, 𝑥 𝑖𝑛 𝑓−1
General Mathematics
Inverse Functions

26. INVERSE FUNCTION
Properties of Inverse Function
1. If f is a one-to-one function, then 𝑓−1
exists.
2. The domain of f is the same as the range of
𝑓−1, and the range of f is the same as the
domain of 𝑓−1
.
3. 𝑓−1
𝑓 𝑥 = 𝑥 for all x in the domain of f;
𝑓(𝑓−1
(𝑥)) = 𝑥 for all x in the domain of 𝑓−1
.
General Mathematics
Inverse Functions

27. INVERSE FUNCTION
Consider the graph, as function 𝒒(𝒙). What
is the domain and range of the function?
𝐷𝑜𝑚 𝑞 }
: 𝑥 1 < 𝑥 ≤ 5
𝑅𝑎𝑛 }
𝑞: 𝑦 3 < 𝑦 ≤ 7
What is the domain and range of 𝒒−𝟏
(𝒙)?
𝑅𝑎𝑛 𝑞−1 }
: 𝑦 1 < 𝑦 ≤ 5
𝐷𝑜𝑚 }
𝑞−1
: 𝑥 3 < 𝑥 ≤ 7
 𝑞−1
(𝑥)
General Mathematics
Inverse Functions

28. INVERSE FUNCTION
 𝑞−1
(𝑥)
The graph of 𝑓(𝑥) and 𝑓−1
(𝑥) are symmetrical to the line 𝑦 = 𝑥.
 𝑦 = 𝑥
General Mathematics
Inverse Functions

29. General Mathematics
Inverse Functions
INVERSE FUNCTION
Example: Below is the graph of the function 𝑚(𝑥). Graph 𝑚−1(𝑥)

30. General Mathematics
Inverse Functions
INVERSE FUNCTION
Step 1: Sketch the line 𝑦 = 𝑥

31. General Mathematics
Inverse Functions
INVERSE FUNCTION
Step 2: Translate the endpoints *𝑚: 𝑎, 𝑏 ⇒ 𝑚−1
: (𝑏, 𝑎)
0,0 ⇒ (0,0)
2,4 ⇒ (4,2)
4,5 ⇒ (5,4)
8,7 ⇒ (7,8)
2, −2 ⇒ (−2,2)
4, −4 ⇒ (−4,4)

32. General Mathematics
Inverse Functions
INVERSE FUNCTION
Step 3: Sketch the graph
0,0 ⇒ (0,0)
2,4 ⇒ (4,2)
4,5 ⇒ (5,4)
8,7 ⇒ (7,8)
2, −2 ⇒ (−2,2)
4, −4 ⇒ (−4,4)

33. SUPPLEMENTARY EXERCISES – inverse functions
1. Sketch y=x
Graph the inverse of the given function
2. Identify points and translate
(0,0) ➔ (0,0)
(1,1) ➔ (1,1)
(2,4) ➔ (4,2)
(3,9) ➔ (9,3)
3. Sketch the graph
General Mathematics
Inverse Functions

34. General Mathematics
Inverse Functions
SUPPLEMENTARY EXERCISES – inverse functions
1. Sketch y=x
Graph the inverse of the given function
2. Identify points and translate
(0,0) ➔ (0,0)
(1,1) ➔ (1,1)
(2,1) ➔ (1,2)
(4,2) ➔ (2,4)
3. Sketch the graph
(-2,2) ➔ (2,-2)
(-1,3) ➔ (3,-1)

35. INVERSE FUNCTION
Properties of Inverse Function
1. If f is a one-to-one function, then 𝑓−1
exists.
2. The domain of f is the same as the range of
𝑓−1, and the range of f is the same as the
domain of 𝑓−1
.
3. 𝑓−1
𝑓 𝑥 = 𝑥 for all x in the domain of f;
𝑓(𝑓−1
(𝑥)) = 𝑥 for all x in the domain of 𝑓−1
.
General Mathematics
Inverse Functions
The third property utilizes the function
operation called “composition” to verify if
functions are inverses of each other.

36. INVERSE FUNCTION
Verifying functions as inverses of each other
Are the equations 𝑦1 =
1
2
𝑥 − 2 and 𝑦2 = 2𝑥 + 4 inverses of each other?
To verify, we use the fact that 𝑓 𝑓−1
𝑥 = 𝑥 = 𝑓−1
(𝑓 𝑥 )
Let 𝑓 𝑥 = 𝑦1 =
1
2
𝑥 − 2 𝑎𝑛𝑑 𝑔 𝑥 = 𝑦2 = 2𝑥 + 4
𝑓 𝑔 𝑥 =
1
2
2𝑥 + 4 − 2
= 𝑥 + 2 − 2
= 𝑥
𝑔 𝑓 𝑥 = 2
1
2
𝑥 − 2 + 4
= 𝑥 − 4 + 4
= 𝑥
Since 𝑓 𝑔 𝑥 = 𝑥 = 𝑔(𝑓 𝑥 ), ∴ they are inverses of each other
General Mathematics
Inverse Functions

37. INVERSE FUNCTION
Given that 𝑓(𝑥) =
1
2
𝑥 − 2 and 𝑔(𝑥) = 2𝑥 + 4 are inverses, what is 𝑓 𝑔 −5 ?
Because they are inverses, then the third property of inverse
functions hold true: 𝒇 𝒇−𝟏
𝒙 = 𝒙 = 𝒇−𝟏
(𝒇 𝒙 )
𝑓 𝑔 −5 =
1
2
2 −5 + 4 − 2
= −5
General Mathematics
Inverse Functions
What about 𝑔 𝑓
𝜋
4
?
=
𝜋
4
This is always true as
long as the two are
inverses of each other.

38. INVERSE FUNCTION
Verify that 𝒇(𝒙) =
𝟐𝒙−𝟏
𝟑
and 𝒈(𝒙) =
𝟑𝒙+𝟏
𝟐
are inverses of each other
To verify, we use the fact that 𝑓 𝑔 𝑥 = 𝑥 = 𝑔(𝑓 𝑥 )
𝑓 𝑔 𝑥 =
2
3𝑥 + 1
2 − 1
3
=
3𝑥 + 1 − 1
3
= 𝑥
Since 𝑓 𝑔 𝑥 = 𝑥 = 𝑔(𝑓 𝑥 ), ∴ they are inverses of each other
=
3𝑥
3
𝑔 𝑓 𝑥 =
3
2𝑥 − 1
3
+ 1
2
=
2𝑥 − 1 + 1
2
= 𝑥
=
2𝑥
2
General Mathematics
Inverse Functions

39. SUPPLEMENTARY EXERCISES – inverse functions
Use the property: 𝑓 𝑔 𝑥 = 𝑥 = 𝑔 𝑓 𝑥
Verify if 𝑓 𝑥 = 𝑥3
+ 2 and 𝑔 𝑥 =
3
𝑥 − 2 are inverses
𝑓 𝑔(𝑥) =
3
𝑥 − 2
3
+ 2
= 𝑥 − 2 + 2
= 𝑥
𝑔 𝑓 𝑥 =
3
𝑥3 + 2 − 2
=
3
𝑥3
= 𝑥
𝑆𝑖𝑛𝑐𝑒 𝑓 𝑔 𝑥 = 𝑥 = 𝑔 𝑓 𝑥 , ∴ 𝑓 𝑎𝑛𝑑 𝑔 𝑎𝑟𝑒 𝑖𝑛𝑣𝑒𝑟𝑠𝑒𝑠
General Mathematics
Inverse Functions
What is 𝑔(𝑓 𝑔 −6 ? Ans. −2

40. SUPPLEMENTARY EXERCISES – inverse functions
Use the property: 𝑓 𝑔 𝑥 = 𝑥 = 𝑔 𝑓 𝑥
Verify if 𝑎 𝑥 = 2𝑥 + 1 and 𝑏 𝑥 = 2𝑥 − 1 are inverses
𝑎 𝑏(𝑥) = 2 2𝑥 − 1 + 1
= 4𝑥 − 2 + 1
= 4𝑥 − 1
𝑏 𝑎 𝑥 = 2 2𝑥 + 1 − 1
= 4𝑥 + 2 − 1
= 4𝑥 + 1
𝑆𝑖𝑛𝑐𝑒 𝑎 𝑏 𝑥 ≠ 𝑥 ≠ 𝑏 𝑎 𝑥 , ∴ 𝑓 𝑎𝑛𝑑 𝑔 𝑎𝑟𝑒 𝑁𝑂𝑇 𝑖𝑛𝑣𝑒𝑟𝑠𝑒𝑠
General Mathematics
Inverse Functions

41. How to find the Inverse of a function?
Step 1: Let 𝒇 𝒙 = 𝒚
𝒚 = 𝟐𝒙 + 𝟑
Step 2: Interchange x and y
𝒙 = 𝟐𝒚 + 𝟑
Step 3: Solve for y
𝟐𝒚 = 𝒙 − 𝟑
𝒚 =
𝒙 − 𝟑
𝟐
Step 4: Represent 𝒚 = 𝒇−𝟏(𝒙)
𝒇−𝟏 𝒙 =
𝒙 − 𝟑
𝟐
Find the inverse of the one-to-one function 𝒇 𝒙 = 𝟐𝒙 + 𝟑

42. How to find the Inverse of a function?
𝒚 =
𝟒
𝒙 − 𝟏
𝒙 =
𝟒
𝒚 − 𝟏
𝒙 𝒚 − 𝟏 = 𝟒
𝒙𝒚 − 𝒙 = 𝟒
𝒙𝒚 = 𝟒 + 𝒙
𝒚 =
𝟒 + 𝒙
𝒙
𝒇−𝟏
𝒙 =
𝟒 + 𝒙
𝒙
Find the inverse of the one-to-one function 𝑓 𝑥 =
4
𝑥−1
, 𝑥 ≠ 1
STEP 1:
STEP 2:
STEP 3:
STEP 4:

43. How to find the Inverse of a function?
Let a and b be elements in the domain
Find the inverse of ℎ 𝑥 =
2𝑥
𝑥+3
Since there is no mention that
the function is one-to-one, we
still need to test if it is indeed
one-to-one. If it is not, there is
no need to find its inverse.
Assume ℎ 𝑎 = ℎ(𝑏)
2𝑎
𝑎+3
=
2𝑏
𝑏+3
2𝑎 𝑏 + 3 = 2𝑏(𝑎 + 3)
𝑎 𝑏 + 3 = 𝑏(𝑎 + 3)
a𝑏 + 3𝑎 = 𝑏𝑎 + 3𝑏
a𝑏 + 3𝑎 = 𝑏𝑎 + 3𝑏
3𝑎 = 3𝑏
𝑎 = 𝑏
∴the function is one-to-one
General Mathematics
Inverse Functions

44. General Mathematics
Inverse Functions
How to find the Inverse of a function?
𝒚 =
𝟐𝒙
𝒙 + 𝟑
𝒙 =
𝟐𝒚
𝒚 + 𝟑
𝒙 𝒚 + 𝟑 = 𝟐𝒚
𝒙𝒚 + 𝟑𝒙 = 𝟐𝒚
𝒙𝒚 − 𝟐𝒚 = −𝟑𝒙
𝒚 𝒙 − 𝟐 = −𝟑𝒙
𝒚 = −
𝟑𝒙
𝒙 − 𝟐
Find the inverse of ℎ 𝑥 =
2𝑥
𝑥+3
STEP 1:
STEP 2:
STEP 3:
STEP 4:
𝒇−𝟏
𝒙 = −
𝟑𝒙
𝒙 − 𝟐

45. How to find the Inverse of a function?
𝒚 = 𝒙𝟑 + 𝟐
𝒙 = 𝒚𝟑 + 𝟐
𝒚𝟑
= 𝒙 − 𝟐
𝒚 =
𝟑
𝒙 − 𝟐
Find the inverse of 𝑓 𝑥 = 𝑥3
+ 2
STEP 1:
STEP 2:
STEP 3: STEP 4:
𝒇−𝟏 𝒙 =
𝟑
𝒙 − 𝟐
General Mathematics
Inverse Functions

46. General Mathematics
Inverse Functions
How to find the Inverse of a function?
𝒚 = 𝟐𝒙 − 𝟑
𝒙 = 𝟐𝒚 − 𝟑
𝒙𝟐 = 𝟐𝒚 − 𝟑
𝟐
𝒙𝟐 = 𝟐𝒚 − 𝟑
𝟐𝒚 = 𝒙𝟐 + 𝟑
𝒚 =
𝒙𝟐 + 𝟑
𝟐
Find the inverse of 𝑟 𝑥 = 2𝑥 − 3; 𝑥 ≥
3
2
and r(x) is one-to-one
STEP 1:
STEP 2:
STEP 3:
STEP 4:
𝒓−𝟏 𝒙 =
𝒙𝟐 + 𝟑
𝟐

47. General Mathematics
Inverse Functions
How to find the Inverse of a function?
You can verify your answer by using the previous method:
𝑓 𝑔 𝑥 = 𝑥 = 𝑔 𝑓 𝑥
𝒓−𝟏 𝒙 =
𝒙𝟐 + 𝟑
𝟐
𝒓 𝒙 = 𝟐𝒙 − 𝟑
𝒓 𝒓−𝟏
𝒙 = 𝟐
𝒙𝟐 + 𝟑
𝟐
𝟑
= 𝒙𝟐 + 𝟑 − 𝟑
= 𝒙𝟐
= 𝒙; 𝑥 ≥
3
2
𝒓−𝟏
𝒓 𝒙 =
𝟐𝒙 − 𝟑
𝟐
+ 𝟑
𝟐
=
(𝟐𝒙 − 𝟑) + 𝟑
𝟐
=
𝟐𝒙
𝟐
= 𝒙

48. SUPPLEMENTARY EXERCISES
Given 𝑎 𝑥 =
2𝑥+1
4
, what is 𝑎−1
𝑎 𝑎−1
4 ?
General Mathematics
Inverse Functions
Determine the inverse 𝑎−1
(𝑥)
𝑦 =
2𝑥 + 1
4
𝑥 =
2𝑦 + 1
4
𝑎−1 𝑥 =
4𝑥 − 1
2
Evaluate 𝑎−1 𝑎 𝑎−1 4
By 3rd property,
it’s equal to 4
𝑎−1 𝑎 𝑎−1 4 = 𝑎−1 4
𝑎−1
4 =
4 4 − 1
2
=
15
2

49. Summary
1. Test if function is one-to-one
𝒊𝒇 𝒇 𝒂 = 𝒇 𝒃 ⇒ 𝒂 𝒔𝒉𝒐𝒖𝒍𝒅 𝒃𝒆 𝒆𝒒𝒖𝒂𝒍 𝒕𝒐 𝒃
Or Horizontal Line Test
2. Test if functions are inverses
Solve 𝒇 𝒈 𝒙 and 𝒈 𝒇 𝒙 , both should be equal to x
3. Solving for inverse of a function
Interchange x and y ➔ solve in terms of y
General Mathematics
Inverse Functions