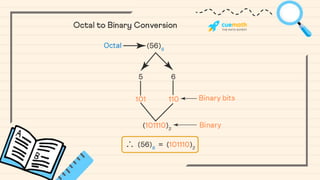
The document discusses number systems. It defines a number system as a system for writing and representing numbers using digits or symbols in a consistent manner. It allows for arithmetic operations and provides a unique representation for every number. The four most common number systems are decimal, binary, octal, and hexadecimal. Binary uses only two digits, 0 and 1, and is used to represent electrical signals in computers. Decimal uses base 10 with digits 0-9 in place values. [END SUMMARY]

1. ICT – CSS 9
NUMBER
SYSTEM

2. WHAT IS NUMBER SYSTEM?
A number system is a system of writing for expressing
numbers. It is the mathematical notation for representing
numbers of a given set by using digits or other symbols in
a consistent manner. It provides a unique representation
to every number and represents the arithmetic and
algebraic structure of the figures. It also allows us to
operate arithmetic operations like addition, subtraction,
and division.

3. Characteristics of Numbering Systems
1)The digits are consecutive.
2)The number of digits is equal to the size of the base.
3)Zero is always the first digit.
4)The base number is never a digit.
5)When 1 is added to the largest digit, a sum of zero and a
carry of one results.
6)Numeric values are determined by the implicit positional
values of the digits.

4. Types of Number System
There are various types of number system in
mathematics. The four most common number system
types are:
1.Decimal number system (Base- 10)
2.Binary number system (Base- 2)
3.Octal number system (Base-8)
4.Hexadecimal number system (Base- 16)

5. 0 = represents no value
1 = represents a unit value
THE BINARY NUMBER SYSTEM
• The binary number system uses 2
digits to encode a number:

6. • That means that you can only use the digits
0 and 1 to write a binary number
Example: some binary numbers
0
1
10
11
1010
and so on.

7. Binary Number System
❑Also called the “Base 2 system”
❑The binary number system is used to model the
series of electrical signals computers use to
represent information
❑0 represents the no voltage or an off state
❑1 represents the presence of voltage or an on state

8. Base 2 Number System
❑Base 2 number systems are also known as Binary number
system wherein, only two binary digits exist, i.e., 0 and 1.
Specifically, the usual base-2 is a radix of 2. The figures
described under this system are known as binary numbers
which are the combination of 0 and 1. For example,
110101 is a binary number.
❑We can convert any system into binary and vice versa

9. DECIMAL NUMBER SYSTEM
Decimal number system has base 10 because it uses
ten digits from 0 to 9. In decimal number system, the
positions successive to the left of the decimal point
represent units, tens, hundreds, thousands and so on.
Every position shows a particular power of the base
(10).

10. Base 10 Number System
This system is expressed in decimal
numbers. The base to the decimal is 10. This
shows that there are ten symbols, 0 to 9.
Similarly, the system using the symbols 0, 1,
two will be of base 3, four symbols will be of
base 4 and so on.

11. Base 10 Number System
This system is expressed in decimal
numbers. The base to the decimal is 10. This
shows that there are ten symbols, 0 to 9.
Similarly, the system using the symbols 0, 1,
two will be of base 3, four symbols will be of
base 4 and so on.

12. Binary ‒to‒ Decimal Process
The Process: Weighted Multiplication
a)Multiply each bit of the Binary Number by it
corresponding bit-weighting factor (i.e. Bit-
0→20=1; Bit-1→21=2; Bit-2→22=4; etc).
b)Sum up all the products in step (a) to get the
Decimal Number.

16. Decimal ‒to‒ Binary Conversion
The Process : Successive Division
a)Divide the Decimal Number by 2; the remainder is
the LSB of Binary Number.
b)If the quotation is zero, the conversion is complete;
else repeat step (a) using the quotation as the
Decimal Number. The new remainder is the next
most significant bit of the Binary Number.

21. A.Binary to Decimal B. Decimal to Binary
1) 10110 2 = ____________ 1. 13 10 = ____________
2) 101010 2 = ____________ 2. 22 10 = ____________
3) 0100101 2 = ____________ 3. 43 10 = ____________
4) 010011 2 = ____________ 4. 158 10 = ____________
5) 11010 2 = ____________ 5. 98 10 = ____________

22. Learning Task 2.
Write 5-sentence essay focusing on what you
have learned. Do not summarize the lesson,
instead discuss new ideas and significant insights
and how the information can be used. Write your
answer on the space provided.

23. ICT – CSS 9
OCTAL TO BINARY

24. In order to convert octal to binary number, we
must follow a few steps. Octal numbers have base 8
and binary numbers have base 2. We can convert the
octal number into decimal and then convert the
decimal number into its equivalent binary number.
Also, we can
remember the octal to the binary equivalent
table to do the quick conversion.

25. Octal Numbers: Octal numbers are the numbers
which have base 8. It is represented as N8. It uses the
digits 0,1, 2, 3, 4, 5, 6 and 7 to represent the numbers
in this number system.
For example:
•1128

30. OCTAL TO BINARY
1. 250
2. 434
3. 620
4. 5722
5.1472

31. The Hexadecimal Numbering System
The base 16, also known
as hexadecimal (abbreviated to hex)
numbering system is regularly used in
computer coding for conveniently
representing a byte or word of data.

32. Hexadecimal, the Base 16 Numbering System
Hexadecimal or "hex" is a numbering system
which uses 16 different numerals. We saw that
decimal used ten numerals from 0 to 9. Hex
expands on this by adding six more, the
capital letters A, B, C, D, E and F.

37. ICT – CSS 9
QUIZ

38. ‘qqqqqqqqqqqqqqqqqqqqqqqqqq
Binary to Decimal
1. 100110112
2. 111011102
3. 001110002
4. 10010111112
5.1101110012

39. ‘qqqqqqqqqqqqqqqqqqqqqqqqqq
Decimal to Binary
1. 6210
2. 1510
3. 8610
4. 4810
5.5510

40. ‘qqqqqqqqqqqqqqqqqqqqqqqqqq
Octal to Binary
1. 1038
2. 4348
3. 14728
4. 226458
5.57228

41. ‘qqqqqqqqqqqqqqqqqqqqqqqqqq
Binary to Octal
1. 1011100102
2. 0101001010102
Hexadecimal to Binary
3. 79E16
4. B0416
5. 13A16

42. ‘qqqqqqqqqqqqqqqqqqqqqqqqqq
Octal to Hexadecimal
1. 14568
2. 66208
3. 153558
4. 14308
5.7428

43. ‘qqqqqqqqqqqqqqqqqqqqqqqqqq
Write an essay focusing on what you have
learned. Do not summarize the lesson, instead
discuss new ideas and significant insights and
how the information can be used. Write your
answer on your notebook.

44. ‘qqqqqqqqqqqqqqqqqqqqqqqqqq
Answer the ff. questions below. Write your answer
on your notebook
1. How important is binary in the world of digital
systems?
2. Why is it important for the students to learn about
binary numbers?
3. What are the benefits of using binary?
4. How do you explain binary to a child?