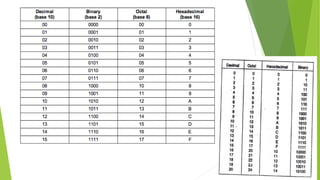
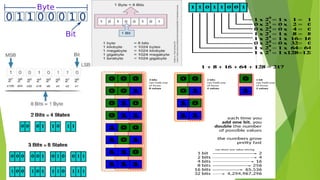
The document covers the fundamentals of boolean algebra and logic circuits with a focus on combinational logic, detailing various number systems including binary, octal, decimal, and hexadecimal. It explains the representation and conversion methods between these number systems, as well as the data units used in computer architecture. Key components such as digital logic gates and combinational logic design procedures are also included.

1. Boolean Algebra and Logic Circuits-
COMBINATIONAL LOGIC
Module 3

2. Contents
 Binary Numbers
 Number Base Conversions
 Octal and Hexa decimal numbers
 Compliments
 Basic Definitions
 Axiomatic definition of Boolean Algebra
 Basic Theorems
 Properties of Boolean Algebra
 Boolean Functions
 Canonical and Standard forms
 Other logic operations
 Digital Logic Gates
 COMBINATIONAL LOGIC:
 Introduction,
 Design procedure,
 Adders- Half Adder and Full adders

3. Number System :
Number System is a way to represent numbers in computer architecture.
There are four different types of the number system, such as:
 Binary number system (base 2)
 Octal number system (base 8)
 Decimal number system(base 10)
 Hexadecimal number system (base 16).

4.  In the number system, each number is represented
by its base.
 If the base is 2 it is a binary number,
 If the base is 8 it is an octal number,
 If the base is 10, then it is called decimal number
system and
 If the base is 16, it is part of the hexadecimal
number system.

5. Binary Number System
 Binary number system is used to define a number in binary
system. Binary system is used to represent a number in terms of
two numbers only, 0 and 1.
 The binary number system is used commonly by computer
languages like Java, C++.
 As the computer only understands binary language that is 0 or
1, all inputs given to a computer are decoded by it into series of
0's or 1's to process it further.

6. Octal Number System
 Octal Number System has a base of eight and uses the numbers
from 0 to 7.
 The octal numbers, in the number system, are usually
represented by binary numbers when they are grouped in pairs of
three.
 For example, an octal number 128 is expressed as 0010102 in the
binary system, where 1 is equivalent to 001 and 2 is equivalent
to 010.
Octal Number System
Base – 8
Octal Symbol – 0, 1, 2, 3, 4, 5, 6 and 7

7. Decimal Number System
 In the decimal number system, the numbers are represented with base 10.
 The way of denoting the decimal numbers with base 10 is also termed as decimal
notation.
 This number system is widely used in computer applications.
 It is also called the base-10 number system which consists of 10 digits, such as,
0,1,2,3,4,5,6,7,8,9.
 Each digit in the decimal system has a position and every digit is ten times more
significant than the previous digit.
 Suppose, 25 is a decimal number, then 2 is ten times more than 5.
 Some examples of decimal numbers are:-
 (12)10, (345)10, (119)10, (200)10, (313.9)10

8.  A number system which uses digits from 0 to 9 to represent a number
with base 10 is the decimal system number.
 The number is expressed in base-10 where each value is denoted by 0 or
first nine positive integers.
 Each value in this number system has the place value of power 10.
 It means the digit at the tens place is ten times greater than the digit at the
unit place. Let us see some more examples:
 (92)10 = 9×101+2×100
 (200)10 = 2×102+0x101+0x100
 The decimal numbers which have digits present on the right side of the
decimal (.) denote each digit with decreasing power of 10.
 Some examples are:
 (30.2)10= 30×101+0x100+2×10-1
 (212.367)10 = 2×102+1×101+2×100+3×10-1+6×10-2+7×10-3

9. Hexadecimal Number System
 The hexadecimal number system is a type of number
system, that has a base value equal to 16.
 It is also pronounced sometimes as ‘hex’.
 Hexadecimal numbers are represented by only 16 symbols.
 These symbols or values are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B,
C, D, E and F. Each digit represents a decimal value.
 For example, D is equal to base-10 13.

11. Decimal to any Base-r
 Decimal to Binary: Divide by 2
 Decimal to Octal: Divide by 8
 Decimal to Hexadecimal: Divide by 16
Any Base-r to Decimal
 Binary to Decimal : Multiply by powers of 2
 Binary to Octal : Multiply by powers of 8
 Binary to Hexadecimal : Multiply by powers of 16

12.  Binary to Octal: Split the given binary numbers into 3 bits and write the
corresponding Octal equivalent.
 Octal to Binary: Write the corresponding binary numbers equivalent for the
given octal numbers.
 Binary to Hexadecimal: Split the given binary numbers into 4 bits and write
the corresponding Hexadecimal equivalent.
 Hexadecimal to Binary: Write the corresponding binary numbers equivalent
for the given Hexadecimal numbers.
 Octal to Hexadecimal: Firstly convert the given Octal number into Binary and
the obtained Binary Value into the Hexadecimal number.
 Hexadecimal to Octal: Firstly convert the given Hexadecimal number into
Binary and the obtained Binary Value into the corresponding Octal number.

13. Data Unit:
• Bit – a binary digit that can have the value 0 or 1
• Nibble – Half of a byte, or 4 bits.
• Byte – 8 Bits
• Word – Two bytes or 16 Bites
• Kilobyte(K) - 210 bytes. (1024 Bytes)
• Megabyte(M) - 220 bytes.(1 million – 1,048,576 Bytes)
• Gigabyte(G) - 230 bytes. (1 billion)
• Terabyte(T) - 240 bytes. (1 trillion)
• Petabyte(P) - 250 bytes.
• Exabyte(P) - 260 bytes.
• Zettbyte(P) – 270 bytes.
• Yottabyte(P) - 280 bytes.