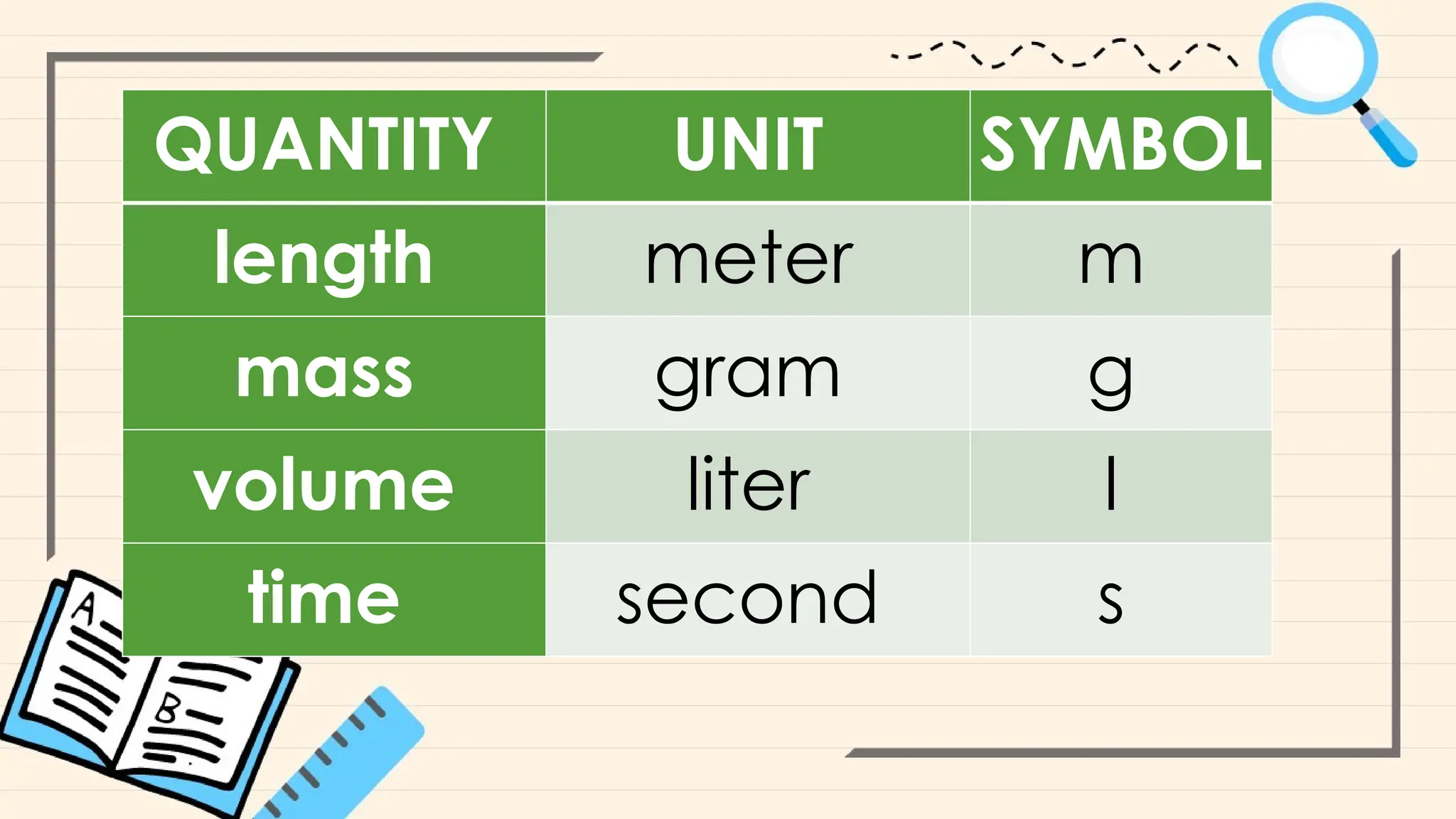
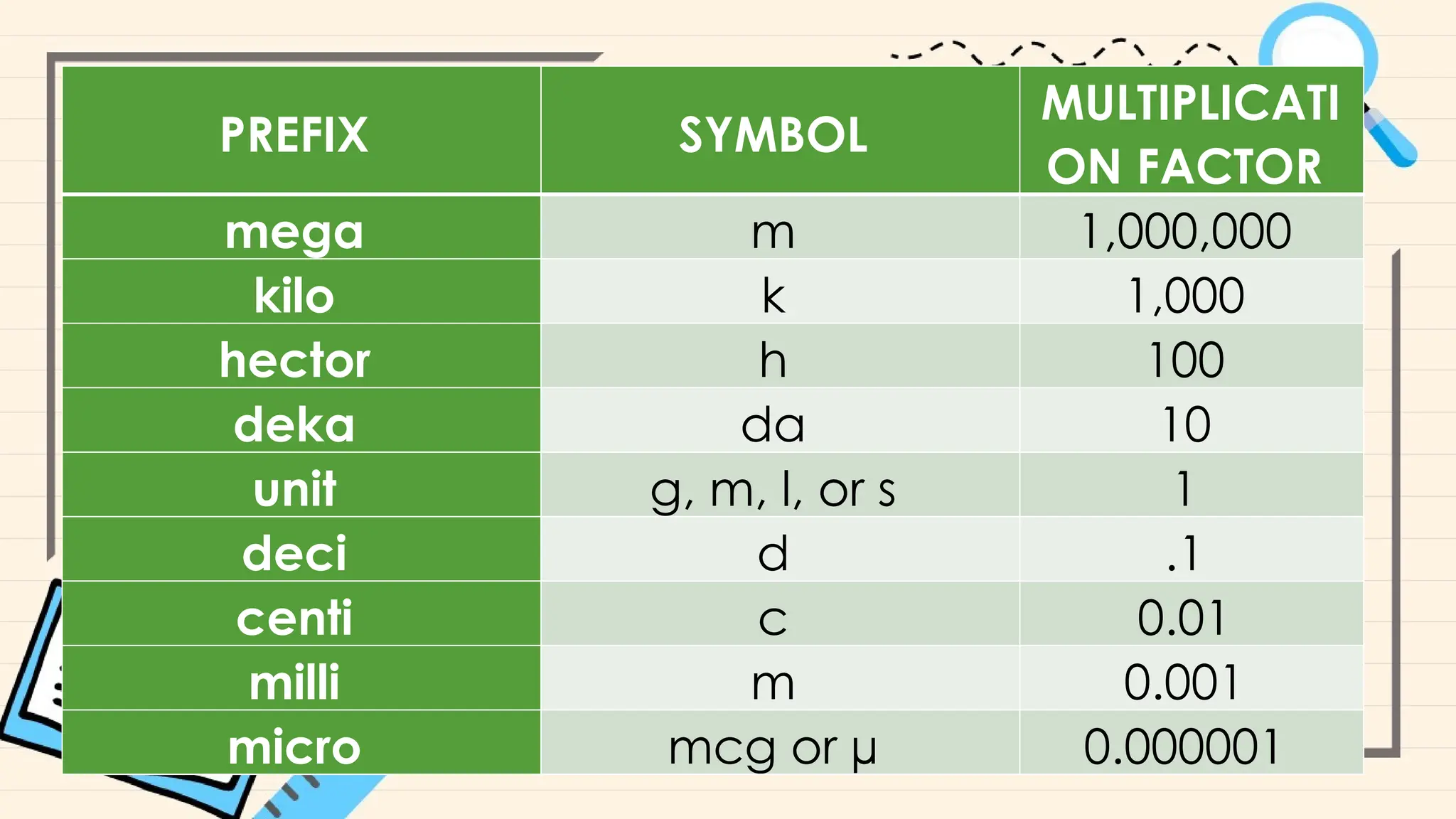
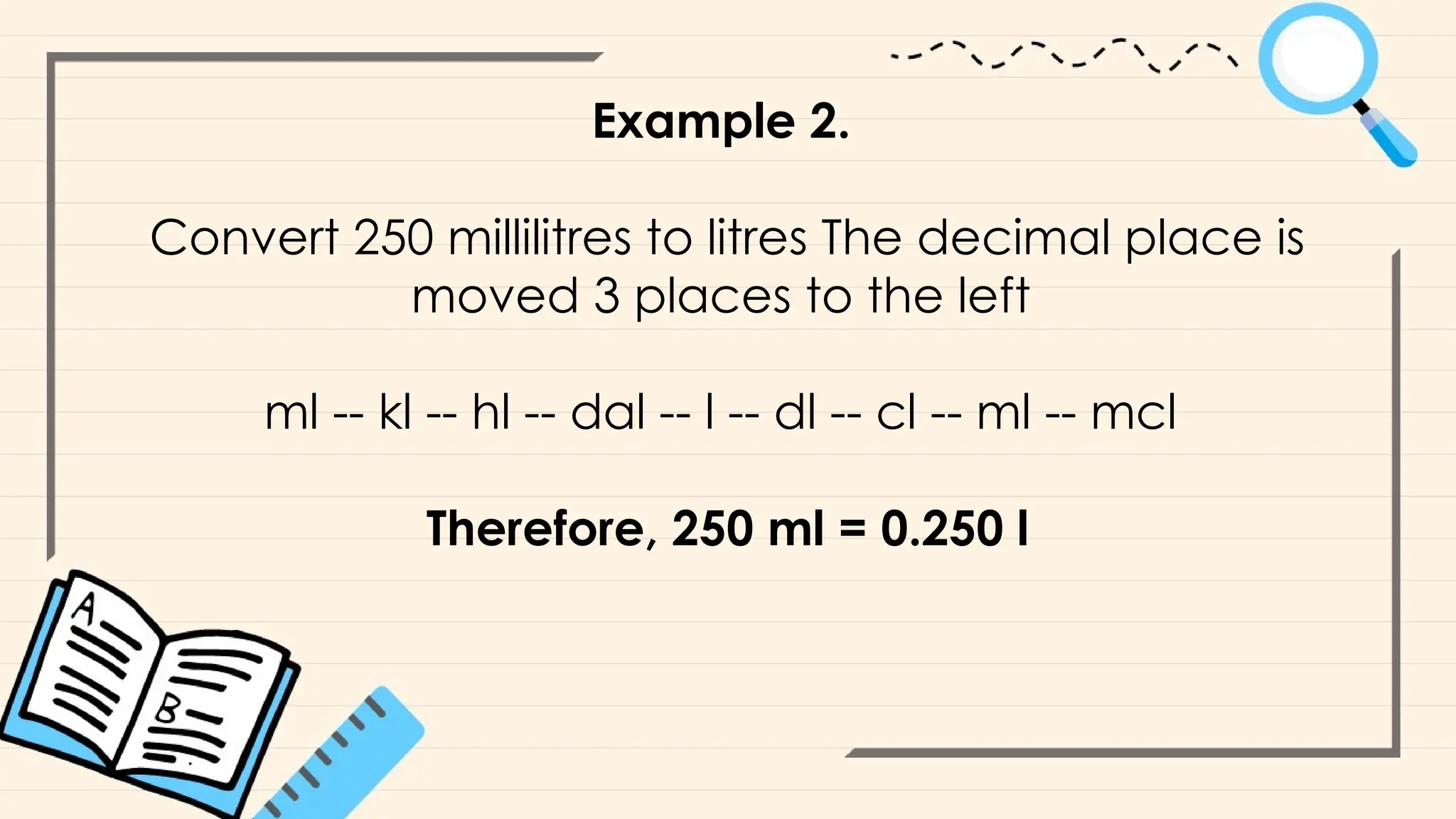
The document provides an overview of basic mathematical concepts such as ratios, fractions, and proportions relevant to caregiving, particularly in drug dosage calculations. It explains how to use these concepts to calculate dosages accurately, including methods for pediatric patients and the importance of understanding drug labels. Additionally, it outlines steps and examples for determining the correct dosages and emphasizes the significance of precise measurements and conversions.


































































![Here is the formula:
Adult dose [ child's age in year ÷ (
child's age in year +12 ) ] =
Approximate child's dose](https://image.slidesharecdn.com/computation-241104111251-bdc9d15f/75/COMPUTATION-pptx-FOR-CAREGIVING-TLE-GRADE-8-74-2048.jpg)

![Computation Based on Young's Rule
500mg [ 2 ÷ ( 2 + 12 ) ] = approximate child's
dose
500mg ( 2 ÷ 14 ) = approximate child's dose
500mg ( .14 ) = approximate child's dose
500mg ( .14 ) = 70 mg
Approximate child's dose = 70 mg](https://image.slidesharecdn.com/computation-241104111251-bdc9d15f/75/COMPUTATION-pptx-FOR-CAREGIVING-TLE-GRADE-8-76-2048.jpg)



![Computation Based on Fried's Rule
500mg [ ( 2 x 12 months ) ÷ 150 ] = approximate child's dose
500mg ( 24 ÷ 150 ) = approximate child's dose
500mg ( .16 ) = approximate child's dose
500mg ( .16 ) = 80 mg
Approximate child's dose = 80 mg](https://image.slidesharecdn.com/computation-241104111251-bdc9d15f/75/COMPUTATION-pptx-FOR-CAREGIVING-TLE-GRADE-8-80-2048.jpg)


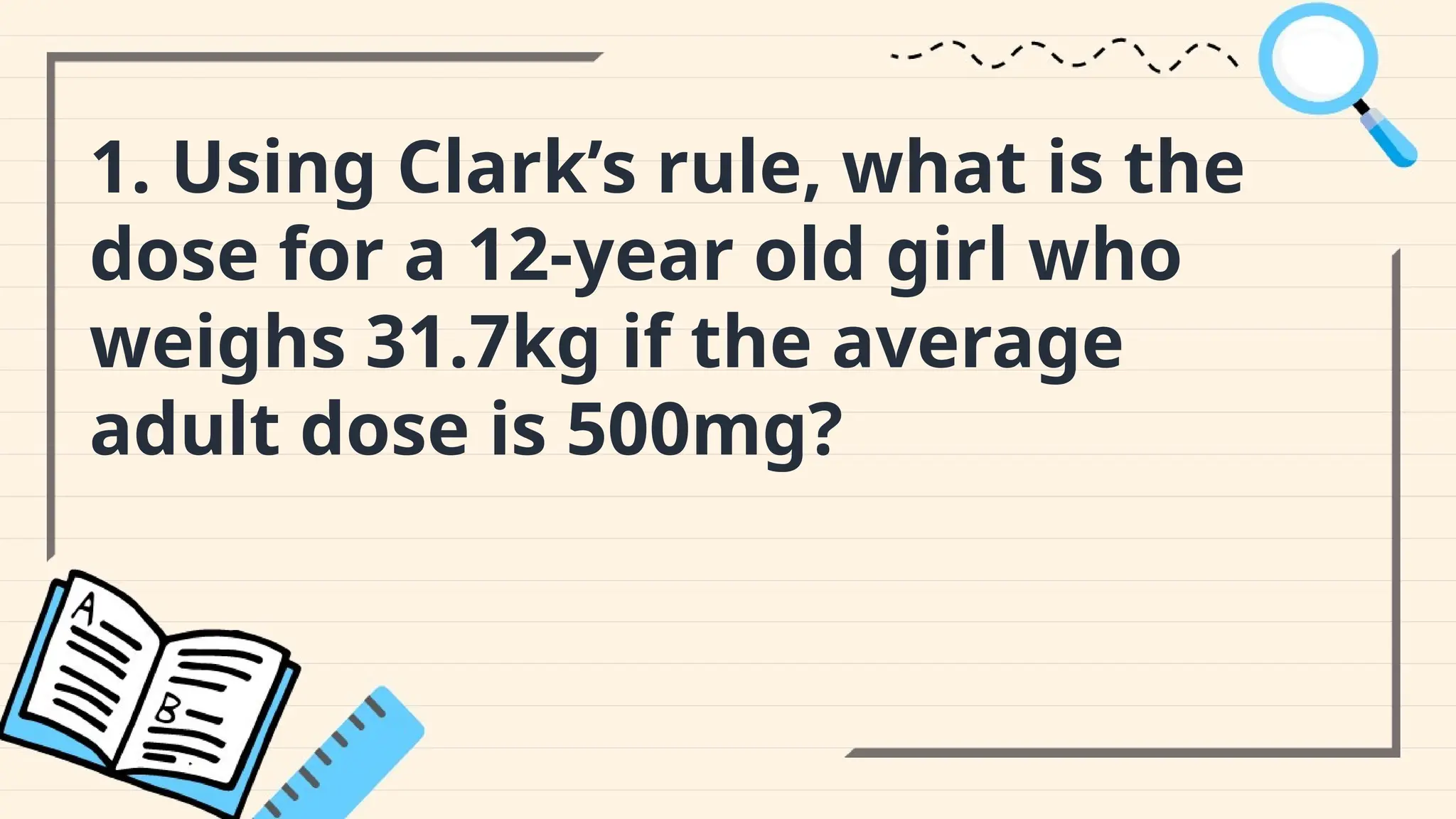




![We can now plug these values into the equation:
•Child’s dose = 200mg x [9 / (9 + 12)]
•Child’s dose = 200mg x [9 / 21]
•Child’s dose = 200mg x 0.43
•Child’s dose = 86mg](https://image.slidesharecdn.com/computation-241104111251-bdc9d15f/75/COMPUTATION-pptx-FOR-CAREGIVING-TLE-GRADE-8-88-2048.jpg)

















