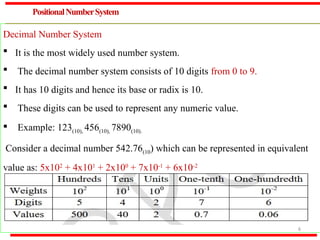
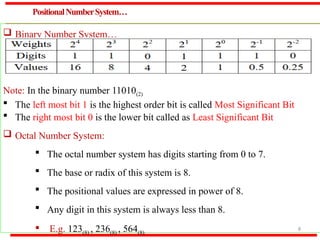
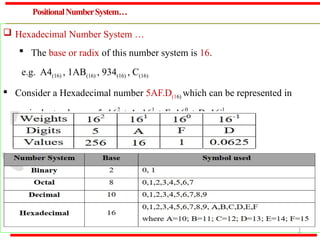
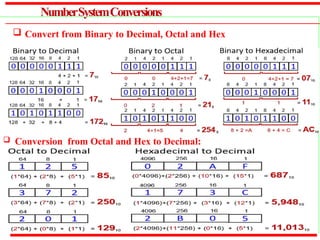
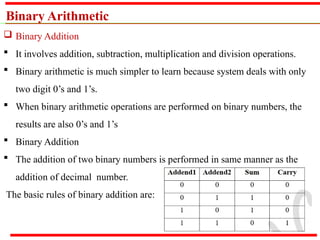
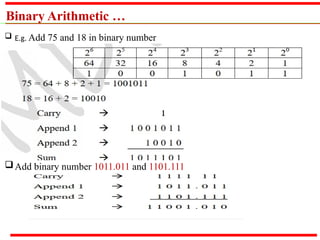
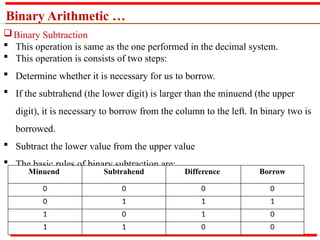
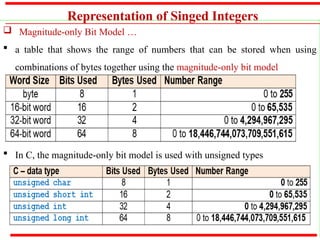
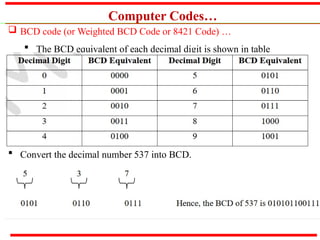
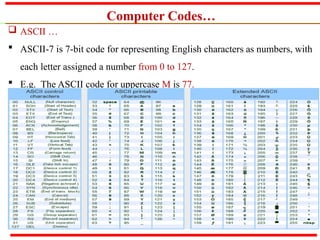
The document outlines various methods of data representation in digital computers, focusing on binary, octal, decimal, and hexadecimal number systems, as well as fixed and floating-point representations of data. It provides details on signed integer representations, including sign-magnitude, one's complement, and two's complement methods. Additionally, it discusses computer codes like ASCII and BCD used for character representation.

1. Chapter Two
DataRepresentation
1

2. Outlin
e
 Bits, bytes, and words
 Numeric data representation and number bases
 Fixed- and floating-point systems
 Signed and twos-complement representations
 Data types
 Representation of nonnumeric data (character codes, graphical data)
 Representation of records and arrays
2

3. Introduction
3
 In Digital Computer, data and instructions are stored in computer memory
using binary code (or machine code) represented by Binary digIT’s 1 and 0
called BIT’s.
 The data may contain digits, alphabets or special character, which are
converted to bits, understandable by the computer.
 The number system uses well defined symbols called digits
 Number systems are basically classified into two types. They are:
 Non-positional number system
 Positional number system

4. Number systems
4
a. Non-positional number system
 In olden days people use of this type of number system for simple
calculations like additions and subtractions.
 The non-positional number system consists of different symbols that are
used to represent numbers.
 E.g. Roman number system, I=1, V=5, X=10, L=50.
 This number system cannot be used effectively to perform arithmetic
operations
b. Positional Number System
 This type of number system are:
 Decimal number system
 Binary number system
 Octal number system
 Hexadecimal number system

5. Number systems
5
b. Positional Number System
 The total number of digits present in any number system is called its Base or
Radix.
 Every number is represented by a base (or radix) x, which represents x digits.
 The base is written after the number as subscript such as
 It is a Decimal number as its base is 10.
 To determine the quantity that the number represents, the number is multiplied
by an integer power of x depending on the position it is located and then finds
the sum of the weighted digits.
 E.g. Consider a decimal number which can be represented in equivalent value
as: 5x102
+ 1x101
+ 2x100
+ 4x10-1
+ 5x10-2

6. PositionalNumberSystem
6
Decimal Number System
 It is the most widely used number system.
 The decimal number system consists of 10 digits from 0 to 9.
 It has 10 digits and hence its base or radix is 10.
 These digits can be used to represent any numeric value.
 Example: 123(10), 456(10), 7890(10).
Consider a decimal number 542.76(10) which can be represented in equivalent
value as: 5x102
+ 4x101
+ 2x100
+ 7x10-1
+ 6x10-2

7. PositionalNumberSystem…
7
Binary Number System
 Digital computer represents all kinds of data and information in the binary
system.
 Binary number system consists of two digits 0 (low voltage) and 1 (high
voltage).
 Its base or radix is 2.
 Each digit or bit in binary number system can be 0 or 1.
 The positional values are expressed in power of 2.
 E.g. 1011(2), 111(2), 100001(2)
 Consider a binary number 11011.10(2) which can be represented in equivalent
value as:

8. PositionalNumberSystem…
8
 Binary Number System…
Note: In the binary number 11010(2)
 The left most bit 1 is the highest order bit is called Most Significant Bit
 The right most bit 0 is the lower bit called as Least Significant Bit
 Octal Number System:
 The octal number system has digits starting from 0 to 7.
 The base or radix of this system is 8.
 The positional values are expressed in power of 8.
 Any digit in this system is always less than 8.
 E.g. 123(8) , 236(8) , 564(8)

9. PositionalNumberSystem…
9
 Octal Number System…
 The number 6418 is not a valid octal number because 8 is not a valid digit.
 Consider a Octal number 234.56(8) which can be represented in equivalent
value as: 2x82
+ 3x81
+ 4x80
+ 5x8-1
+ 6x8-2
 Hexadecimal Number System
 The hexadecimal number system consists of 16 digits from 0 to 9 and A to F.
 The letters A to F represent decimal numbers from 10 to 15.
 That is, ‘A’ represents 10, ‘B’ represents 11, ‘C’ represents 12, ‘D’ represents
13, ‘E’ represents 14 and ‘F’ represents 15.

10. PositionalNumberSystem…
1
0
 Hexadecimal Number System …
 The base or radix of this number system is 16.
e.g. A4(16) , 1AB(16) , 934(16) , C(16)
 Consider a Hexadecimal number 5AF.D(16) which can be represented in
equivalent value as: 5x162
+ Ax161
+ Fx160
+ Dx16-1

11. NumberSystemConversions
 Conversion from Octal and Hex to Decimal:
 Convert from Binary to Decimal, Octal and Hex

12. Cont’d…
 Convert from Decimal to Binary and Hex:

13. Binary Arithmetic
 Binary Addition
 It involves addition, subtraction, multiplication and division operations.
 Binary arithmetic is much simpler to learn because system deals with only
two digit 0’s and 1’s.
 When binary arithmetic operations are performed on binary numbers, the
results are also 0’s and 1’s
 Binary Addition
 The addition of two binary numbers is performed in same manner as the
addition of decimal number.
The basic rules of binary addition are:

14. Binary Arithmetic …
 E.g. Add 75 and 18 in binary number
Add binary number 1011.011 and 1101.111

15. Binary Arithmetic …
Binary Subtraction
 This operation is same as the one performed in the decimal system.
 This operation is consists of two steps:
 Determine whether it is necessary for us to borrow.
 If the subtrahend (the lower digit) is larger than the minuend (the upper
digit), it is necessary to borrow from the column to the left. In binary two is
borrowed.
 Subtract the lower value from the upper value
 The basic rules of binary subtraction are:
Minuend Subtrahend Difference Borrow
0 0 0 0
0 1 1 1
1 0 1 0
1 1 0 0

16. Binary Arithmetic …
Binary Subtraction
When we subtract 1 from 0, it is necessary to borrow 1 from the next left
column i.e. from the next higher order position
E.g. Subtract the following number
a) 10 from 14 b) 9 from 29 c) 3 from 5
e.g. Add 75 and -18 in binary number.
75 = 64 + 8 + 2 + 1 = 1001011
18 = 16 + 2 = 10010

17. Data representation in computer
 Data is representation using binary numbers in terms of 0’s and 1’s
 Bit- is representation of 1 or 0
 Nibble: is a group of four consecutive bits
 Byte: is a group of eight consecutive bits
 A group of two nibbles can form a byte
 Word: is a group of 16 bits, 32bits or 64 bits
 It is also group two, four or 8 bytes together form a word
 When we working in hexadecimal calculations since each hexadecimal
digit is represented with a nibble
 When grouping bits of 1’s and 0’s together, there are a variety of methods
for interpreting them.
 Each method of interpreting the sequence of bits is called a bit model.

18. Representation of Singed Integers
 The digital computer handle both positive and negative integer.
 It means, is required for representing the sign of the number (- or +), but
cannot use the sign (-) to denote the negative number or sign (+) to
denote the positive number.
 this is done by adding the leftmost bit to the number called sign bit.
 A positive number has a sign bit 0, while the negative has a sign bit 1.
 It is also called as fixed point representation
 A negative signed integer can be represented in one of the following:
 Sign and magnitude method
 One’s complement method
 Two’s complement method

19. Representation of Singed Integers …
 Magnitude-only Bit : this model is for non-negative decimal numbers
 It is the simplest model since each bit represents an integer power of 2.
 With an 8-bit value, the store a value is in the range of 0 to 255.
00000000 = 0
00000001 = 1
00000010 = 2
00000011 = 3
… Magnitude only
11111101 = 253
11111110 = 254
11111111 = 255
 In this representation, the left most bit is considered the most-significant bit
and the rightmost bit as the least-significant bit. (e.g., 10110101)
 When adding numbers, adding bits together starting from the least-
significant bit to the most-significant bit

20. Representation of Singed Integers
 Magnitude-only Bit Model …
 Notice that there can be an overflow.
 There is a limit to the values that can store with just one byte. Hence, we often use
more than one byte to represent numbers in our software.
 When dealing with combinations of bytes, we can have groups of 8 bits to store
words to provide a larger range of values.
 E.g. sequence of 4 bytes can represent: 10011001 00001110 01111001 00111001
= (10011001 * 224) + (00001110 * 216) + (01111001 * 28) + (00111001 * 20)
= (153 * 16,777,216) + (14 * 65,536) + (121 * 256) + (57 * 1)
= 2,567,862,585

21. Representation of Singed Integers
 Magnitude-only Bit Model …
 a table that shows the range of numbers that can be stored when using
combinations of bytes together using the magnitude-only bit model
 In C, the magnitude-only bit model is used with unsigned types

22. Representation of Singed Integers…
 Sign-Magnitude Bit : allows negative decimal numbers
 It is the simplest strategy for representing negative numbers.
 It has a smaller magnitude range of -127 to +127 for a single byte.
 The most- significant bit use as sign bit
 0 positive sign bit value and 1  a negative value.
00000000 = 0
00000001 = 1
00000010 = 2
…
01111110 = 126 sign magnitude
01111111 = 127
10000000 = -0
10000001 = -1
10000010 = -2
…
11111110 = -126
11111111 = -127

23. Representation of Singed Integers…
 Sign-Magnitude Bit Model…
 If the signs of the two numbers are the same, we simply add the magnitudes as
unsigned numbers and leave the sign bit intact
 However, we need to be careful about overflow
 If the signs differ, we need to subtract the smaller magnitude from the
larger magnitude, and keep the sign of the larger magnitude

24. Representation of Singed Integers…
 1’s Complement representation
 This is the simplest method of representing negative binary number.
 The 1’s complement of a binary number is obtained by changing each 0 to
1 and each 1 to 0.
 In other words, change each bit in the number to its complement.
 Example 1: Find the 1’s complement of 101000.
 Ex :Find the 1’s complement of 1010111

25. Representation of Singed Integers…
 2’s Complement representation:
 The 2’s complement of a binary number is obtained by taking 1’s
complement of the number and adding 1 to the Least Significant Bit
(LSB) position.
 The general procedure to find 2’s complement is given by:
 2’s Complement = 1’s Complement + 1
 Find the 2’s complement of 101000.
 Original number
 1’s complement
 Add 1 to LSB
 2’s complement

26. Bit Models…
 2’s Complement …
 To determine the magnitude of a negative number, we perform the exact same
steps:
11101101 = -19
00010010 flip bits
00010011 add one
00010011 = 19 magnitude
 Negation: It is the operation of converting
a positive number to its negative equivalent
or a negative number to its positive
equivalent. Negation is performed by
performing 2’s complement system.
 Example 1: Consider the number +12. Its
binary representation is 01100(2).
Ee. Find the 1’s and 2’s complement of 1011101.

27. Fixed- and floating-point systems
 Real Numbers - numbers with fractional component
 Two major approaches to store real numbers •
 Fixed Point Notation
 Floating Point Notation.
 Fixed point notation -there are a fixed number of digits after the decimal
point (Integer . Fraction)
 This representation has fixed number of bits for integer part and for
fractional part.
 E.g. if given fixed-point representation is IIII.FFFF, then you can store
minimum value is 0000.0001 and maximum value is 9999.9999.
 There are three parts of a fixed-point number representation:
 the sign field, integer field, and fractional field

28. Fixed- and floating-point systems
 Fixed point notation …
We can represent these numbers using:
 signed representation: range -(2(k-1)
-1) to (2 (k-1)
-1) for k-bits
 1’s complement representation: range -(2(k-1) -1) to (2 (k-1) -1) for k-bits
 2 ‘s complement representation: range -(2(k-1) -1) to (2 (k-1) -1) for k-bits
 2’s complementation representation is preferred in computer system
because of unambiguous property and easier for arithmetic operations.
 E.g. Assume number is using 32-bit format which reserve 1 bit for the sign, 15
bits for the integer part and 16 bits for the fractional part.
 -43.625 is represented as

29. Fixed- and floating-point systems
 Fixed point notation …
 0 is used to represent positive and 1 is used to represent negative
 000000000101011 is 15 bit binary value for decimal 43 and
1010000000000000 is 16 bit binary value for fractional 0.625

30. Fixed- and floating-point systems
 Floating point number - allows for a varying number of digits after the
decimal point (Integer . Fraction)
 does not reserve a specific number of bits for the integer part or the
fractional part.
 The floating number representation of a number has two part:
 The first part represents a signed fixed point number called mantissa
 The second part of designates the position of the decimal(or binary) point
and is called exponent.
 The fixed point mantissa may be fraction or an integer.
 Floating -point is always interpreted to represent a number in mantissa m
and exponent e are physically represented in the register (including sign).

31. Fixed- and floating-point systems
 A floating-point number is said to be normalized if the most significant
digit of the mantissa is 1
 actual number is (-1)s
(1+m)x2(e-Bias
), where s is the sign bit, m is the
mantissa, e is the exponent value, and Bias is the bias number
 According to IEEE 754 standard, the floating-point number is represented
in following ways:
 Half Precision (16 bit): 1 sign bit, 5 bit exponent, and 10 bit mantissa
 Single Precision (32 bit): 1 sign bit, 8 bit exponent, and 23 bit mantissa
 Double Precision (64 bit): 1 sign bit, 11 bit exponent, and 52 bit mantissa
 Quadruple Precision (128 bit): 1 sign bit, 15 bit exponent, and 112 bit
mantissa

32. Fixed- and floating-point systems
E.g. Suppose number is using 32-bit format: the 1 bit sign bit, 8 bits for signed
exponent, and 23 bits for the fractional part.
The leading bit 1 is not stored (as it is always 1 for a normalized number) and
is referred to as a “hidden bit”.
 Then −53.5 is normalized as -53.5=(-110101.1)2=(-1.101011)x25
, which is
represented as following below,
 00000101 is the 8-bit binary value of exponent value +5.

33. Computer Codes
 Computer code helps us to represent characters in a coded form in the
memory of the computer.
 These codes represent specific formats which are used to record data.
 Some of the commonly used computer codes are:
 Binary Coded Decimal (BCD)
 Extended Binary Coded Decimal Interchange Code (EBCDIC)
 American Standard Code for Information Interchange (ASCII)
 BCD code (or Weighted BCD Code or 8421 Code)
 BCD stands for Binary Coded Decimal.
 It is one of the early computer codes.
 In this coding system, the bits are given from left to right, the weights
8,4,2,1 respectively.

34. Computer Codes…
 BCD code (or Weighted BCD Code or 8421 Code) …
 The BCD equivalent of each decimal digit is shown in table
 Convert the decimal number 537 into BCD.

35. Computer Codes…
 BCD code (or Weighted BCD Code or 8421 Code) …
 In 4-bit BCD only 24
=16 configurations are possible which is insufficient
to represent the various characters.
 Hence 6-bit BCD code was developed by adding two zone positions with
which it is possible to represent 26
=64 characters
 EBCDIC
 It stand for Extended Binary Coded Decimal Interchange Code.
 This was developed by IBM.
 It uses an 8-bit code and hence possible to represent 256 different
characters or bit combinations
 EBCDIC is used on most computers and computer equipment today.

36. Computer Codes…
 EBCDIC…
 It is a coding method generally used by larger computers (mainframes) to
present letters, numbers or other symbols in a binary language the
computer can understand
 EBCDIC is an 8-bit code; therefore, it is divided into two 4-bit groups,
where each 4-bit can be represented as 1 hexadecimal digit.
 ASCII
 It stands for the American Standard Code for Information Interchange.
 It is a 7-bit code, which is possible to represent 27=128 characters.
 It is used in most microcomputers and minicomputers and in mainframes.
 ASCII code (Pronounced ask-ee) is of two types – ASCII-7 and ASCII-8

37. Computer Codes…
 ASCII …
 ASCII-7 is 7-bit code for representing English characters as numbers, with
each letter assigned a number from 0 to 127.
 E.g. The ASCII code for uppercase M is 77.

38. Representation of records and arrays
 A record is a data structure made up of a fixed number of information items,
not necessarily of the same type.
 Records are useful when the items are to be referred to by name
 In C records are of the type structure.
 An array is a data structure made up of a fixed number of information items
in sequence; all items are required to be of the same type.
 arrays are useful when the items are to be referred to by their positions in the
 sequence.
 Records and arrays allow related items of information to be treated as a
group

39. End of Chapter Two
Any
Question ???