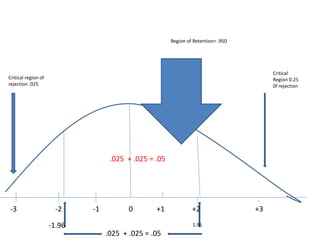
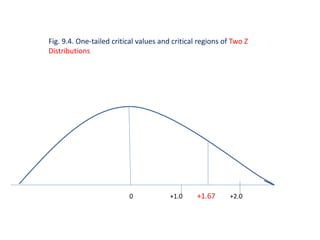
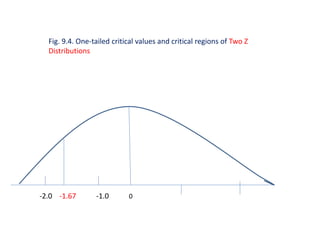
The document discusses key concepts related to p-values and significance testing. It defines a p-value as the likelihood that a difference detected is due to chance rather than a true effect. A difference is considered statistically significant if the p-value is less than 0.05, meaning there is less than a 5% chance the difference is due to random error. The document also discusses critical values, which are numerical cut-offs used to determine whether to reject or retain the null hypothesis, and types I and II errors that can occur in significance testing.

1. P-Value
Desmond Ayim-Aboagye, Ph.D.
Significance Level

2. P-Value
• When a statistic is said to be significant at the 0.05
level, for example, the likelihood that the difference it
detected is due to chance (i.e., random error) is less
than 1 in 20.
• In other words, if the experimenter were repeated 100
times, we would expect to observe the same results by
chance– not due to the effect an independent variable
exerts on a dependent measure– 5 time or less.
• No difference is deemed to be reliable one unless it
reaches or is still lower than this conventional 5
percent mark or 0.05 level of significance.

3. .025 + .025 = .05
-3 -2 -1 0 +1 +2 +3
Critical
Region 0.25
0f rejection
Region of Retention= .950
Critical region of
rejection .025
.025 + .025 = .05
-1.96 1.96

4. A critical value
• A critical value is a numerical value that is
compared to the value of a calculated test
statistic. When a test statistic is less than a
critical value, the null hypothesis is accepted
or retained. When a test statistic is equal to or
higher than a critical value, then the null
hypothesis is rejected.

5. A critical value
It is a cut off, a guide to whether a test
statistic is or is not significant

6. 0 +1.0 +1.67 +2.0
Fig. 9.4. One-tailed critical values and critical regions of Two Z
Distributions

7. -2.0 -1.67 -1.0 0
Fig. 9.4. One-tailed critical values and critical regions of Two Z
Distributions

8. Two-tailed Significance Test
Two-tailed Significance Tests
promote rigor, as well as satisfy
curiosity when predictions go awry.

9. Degree of Freedom
• It is a statistical concept
• The degree of freedom in any set of data are the
number of scores that are free to take on any
value once some statistical test is performed.
• It can be known by taking the total number of
available values , that is, SAMPLE SIZE, and then
subtracting the number of population parameters
that will be estimated from the sample.

10. More Stringent Requirement
• 100 trials, the 1 percent or 0.01 level of
significance.
• More demanding p- value of 0.001, which
indicates over 1000 trials, there is only one
chance of obtaining a predicted difference
when the null hypothesis is actually true.

11. Most Behavioural Scientists
• Most researchers choose to use .05 level of
significance as the minimum acceptable level
of significance.
• P-values
• P < .05
• P < .01
• P < .001

12. Inferential Errors Types I and II
• The H0 is not rejected because H0 is true. This is a
correct decision.
• The H0 is rejected because of H0 is false. This is a
correct decision.
• The H0 is rejected but H0 is true. This is an
incorrect decision known as the Type 1 error.
•

13. Type I Error
• A type I error involves rejecting the null
hypothesis – a researcher believes that a
significant difference is found – when, in fact,
there is actually no difference, so that the null
hypothesis is true. A type I error occurs when
a researcher finds a difference where one
does not exist.
• α error, correct decision (1-α)

14. Type II Error
• Type II error involves accepting the null
hypothesis – a researcher believes that no
significance difference is present – when, in
fact, there is actually a difference, so that the
null hypothesis is a false. A type II error occurs
when a researcher fails to find a difference
where one exists.
• β error, correct decision (1-β)