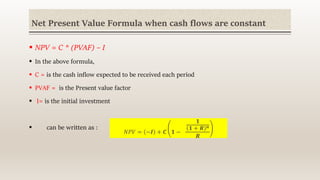
The document discusses investment criteria in capital allocation, focusing on methods such as Net Present Value (NPV) and Payback Period, distinguishing their advantages and disadvantages. NPV helps assess the value of investments based on future cash flows and opportunity cost, while the Payback Period estimates the time needed to recover an initial investment without considering the time value of money. Additionally, it introduces the Discounted Payback Period as a refinement of the Payback Period that incorporates the time value of money.

1. SHAH ABDUL LATIF UNIVERSITY,
GHOTKI CAMPUS
DEPARTMENT OF BUSINESS
ADMINISTRATION

2. PROJECT EVALUATION
COURSETITLE
Course Instructor: Nadia Memon
Batch: BBA-Part IV 2017
Lecture Topic: Different Investment criteria

3. Topics of Discussion
 Process of Capital allocation
 Net Present Value
 Payback period
 Discounted Payback period

4. Capital allocation decisions
 The process of allocating capital is more than just
deciding whether to buy a fixed asset.
 Capital allocation is deciding about nature of firm’s
operation for years to come. The projects and assets
firm select for capital investment usually define
business of that firm.
 Decisions such as these are not easily reversed, once
they are made, that’s why firms make careful strategic
choices that will reap some profit for them.
 Most the firms possess huge possible investments, each
one is option available to firm, some options are
valuable, some are not, firms must learn to identify
which are which? With useful techniques discussed in
this lecture.

5. 1. Net Present Value
 An investment is worth undertaking if it creates value for its owners.
 Investment is said to be valuable if it is worth more in the marketplace than
it costs to acquire.
 “Net present value is the difference between an investments
market value and its cost commonly known as NPV”.
 Suppose you buy a car for Rs. 250,000 and spend another 40,000 on it to get
it fixed up, your total investment is 290,000, now you place the car back in
the market and find that it worth 350,000, the market value exceeds the cost
by 60,000 results in value you have created for the investment.

6. Net Present Value
 Net present value requires to estimate the future cash flows of investment
opportunity based on realistic assumptions.
 Appropriate discounted rate is identified to discount the future cash flows,
that rate will be based on opportunity cost of capital, means how much rate
we could earn if we invest same amount in any other project/option.
 Net present value will be calculated by subtracting present value of future
cash flows from present value of cash inflows.
 NPV = PV cash inflows – PV cash outflows

7.  Acceptance Rule
 Accept the project when NPV is positive NPV > 0
 Reject the project when NPV is negative NPV < 0
 May accept the project or indifferent between taking and not taking the
project when NPV is zero NPV = 0
Net Present Value

8.  NPV = C * (PVAF) – I
 In the above formula,
 C = is the cash inflow expected to be received each period
 PVAF = is the Present value factor
 I= is the initial investment
 can be written as :
Net Present Value Formula when cash flows are constant
𝑁𝑃𝑉 = −𝑰 + 𝑪 𝟏 −
𝟏
𝟏 + 𝑹 𝒏
𝑹

9. Net Present Value Formula when cash flows are constant
 Example
 Calculate the net present value of a project which requires an initial investment of Rs.
243,000 and it is expected to generate a cash inflow of Rs. 50,000 each month for 12
months. Assume that the salvage value of the project is zero. The target rate of return is
12% per annum.
 We have,
 Initial Investment = Rs: 243,000
 Net Cash Inflow per Period = Rs:50,000
 Number of Periods = 12
 Discount Rate per Period = 12% ÷ 12 = 1%

10. Add a Slide Title - 3
 Net Present Value =C * PVAF - I
= 50,000 × 11.255 − 243,000
= 562,750 − 243,000
= 319,750
net present value is positive investment should be accepted
Net Present Value Formula when cash flows are constant

11.  The formula for the net present value can be written as follows:
𝑁𝑃𝑣 =
𝐶1
1+𝑅
+
𝐶2
1+𝑅 2 +
𝐶3
1+𝑅 3
+
𝐶 𝑛
1+𝑅 𝑛
}- I
𝑁𝑃𝑣 =
𝑐 𝑡
1+𝑅 𝑡
− 𝐼
 Where as C1,C2…Cn represents net cash inflow for year 1,2….n
 K is the opportunity cost of capital or return rate
 I is the initial investment n is the expected life of investment
Net Present Value Formula when cash flows are uneven

12. Example
 Assume that Project X costs Rs 2,500 now and is expected to generate year-
end cash inflows of Rs 900, Rs 800, Rs 700, Rs 600 and Rs 500 in 5 years,
The opportunity cost of the capital may be assumed to be 10 per cent.
 𝑵𝑷𝒗 =
𝟗𝟎𝟎
𝟏+𝟎⋅𝟏𝟎 𝟏 +
𝟖𝟎𝟎
(𝟏+𝟎.𝟏𝟎) 𝟐 +
𝟕𝟎𝟎
𝟏+𝟎.𝟏𝟎 𝟑 +
𝟔𝟎𝟎
(𝟏+𝟎.𝟏𝟎) 𝟒 +
𝟓𝟎𝟎
(𝟏+𝟎.𝟏𝟎) 𝟓 − 𝟐𝟓𝟎𝟎
 Find out the solution .
 Answer = 225

13. Net present Value Merits and Flaws
 NPV gives important to the time value of money.
2.In the calculation of NPV, both after cash flow and before cash
flow over the life span of the project are considered.
3. Profitability and risk of the projects are given high priority.
4. NPV helps in maximizing the firm's value.

14. Net present Value Merits and Flaws
 NPV is difficult to use.
2. NPV can not give accurate decision if the amount of investment
of mutually exclusive projects are not equal.
3. It is difficult to calculate the appropriate discount rate.
4. NPV may not give correct decision when the projects are of
unequal life.

15. 2. The Payback Period
 The payback is the length of time it takes to recover our initial investment
 payback period is the amount of time required for an investment to
generate cash flows sufficient to recover its initial cost.
 It is the common practice to talk about that in how much time our
investment pays back and we will get our initial investment fully paid,
usually management as well as common investors interested more in the
projects that payback in shortest possible time that’s why is technique is
widely used to estimate the possible time and desirability of projects.

16. Based on the payback rule, an investment is acceptable if
its calculated payback period is less than some
prespecified number of years.
For suppose we have 500,000 rupees and we wanted to invest them to secure
our investment as we have different options available, like shares, bank
investment, private partnership, real state and so on, but we want to get our
investment generate inflows in less possible time so we can apply payback
period method and can estimate cash flows of desirable options available and
calculate payback period.
The Payback Rule

17. Two Content Layout with Table
 The projects initial investment is 500,000
 What is the payback period for this investment when
cash flows are these?
 The initial investment is 500,000. After the first two
years, total cash inflows are 300,000, after third year,
the total cash fl ow is 800,000
 It means the project pays back between the end of
year 2 and in the start of year 3. Because the
accumulated cash flows for the first two years are
300,000 we need to recover 200,000 in the third
year.
 The third-year cash fl ow is $500, so we will have to
wait 200,000/500,000= .4 year to do this. The
payback period is thus 2.4 years, or about two years
and four months.
Year Cash flow
0 -500,000
1 100,00
2 200,000
3 500,000
The Payback period

18.  Many decisions simply do not warrant detailed analysis because the cost of
the analysis would exceed the possible loss from a mistake.
 Small investment decisions are made by the hundreds every day in large
organizations, so this technique is less time consuming.
 First, because it is biased toward short-term projects, it is biased toward
liquidity.
 The payback period is a kind of “break-even” measure. Because time value is
ignored,
The Payback period Redeeming Qualities

19.  we calculate the payback period by simply adding up the future cash flows.
There is no discounting involved, so the time value of money is completely
ignored.
 The payback rule also fails to consider any risk differences. The payback
would be calculated the same way for both very risky and very safe projects.
 payback period rule is coming up with the right cutoff period, using a
number that is arbitrarily chosen, there is no guide how to pick a cutoff.
 Biased against long-term projects, such as research and development, and
new projects, as we can not clearly estimate when they payback.
The Payback period Shortcomings of the rule

20. Year Cash flow
0 -4,800
1 1500
2 2600
3 2900
4 1700
Payback period Example
 Calculating Payback What is the payback period for the following set of cash flows?
 To calculate the payback period, we need to find the time that the project has recovered
its initial investment. After two years, the project has created,
 $1,500 + 2,600 = $4,100
 in cash flows. The project still needs to create another:
 $4,800 – 4,100 = $700
 During the third year, the cash flows from the project will be $2900.
 So, the payback period will be 2 years, plus months
 The payback period is:
 Payback = 2 + ($700 / $2,900) = 2.24 years

21.  Definition
 The discounted payback period is the length of time until the sum of the
discounted cash flows is equal to the initial investment.
 The major shortcoming of the payback period rule was that it ignored time
value of money, so this improved version fixed this issue.
 Discounted payback is closely associated with NPV because when it pays
back, there must be a positive NPV due to initial investment is retrieved.
 Discounted payback is an improvement on regular payback because it
considers the time value of money.
3. Discounted Payback period

22.  The discounted payback is calculated the same as is regular payback, with the exception that
each cash flow in the series is first converted to its present value.
 Thus discounted payback provides a measure of financial break-even because of this
discounting, just as regular payback provides a measure of accounting break-even because it
does not discount the cash flows.
 Based on some predetermined cutoff for the discounted payback period, the decision rule is
to accept projects whose discounted cash flows payback before this cutoff period, and to
reject all other projects.
 The primary disadvantage to using the discounted payback method is that it ignores all cash
flows that occur after the cutoff date, thus biasing this criterion towards short-term
projects. As a result, the method may reject projects that in fact have positive NPVs.
Discounted Payback period rule

23. Example
 Calculating Discounted Payback
 An investment project has annual cash inflows of $6,500, $7,000, $7,500, and $8,000, and a
discount rate of 14 percent. What is the discounted payback period for these cash flows if
the initial cost is $8,000?
 When we use discounted payback, we need to find the value of all cash flows today. The
value today of the project cash flows for the first four years is:
year Discounting PV of cash flow
0 - 8000
1 6500
1 ⋅ 14 1
5,701.75
2 7000
1 ⋅ 14 2
5,386.27
3 7500
1 ⋅ 14 3
5,062.29

24.  To find the discounted payback, we use these values to find the payback period. The
discounted first year cash flow is $5,701.75, so the discounted payback for an $8,000 initial
cost is:
 We will subtract first year's cash flow from initial investment because payback is highly
likely to occur in second year.
 Discounted payback = ($8,000 – 5,701.75)= 2298.25
 Discounted payback = 1+ 2298.25/$5,386.27 = 1.43 years
Example

25. HAVE A GREAT DAY !