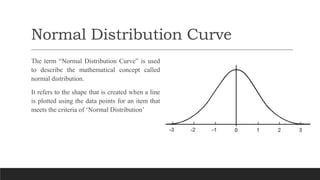
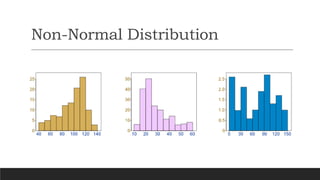
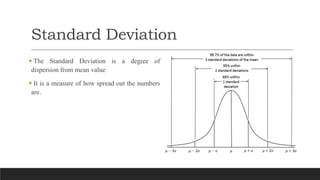
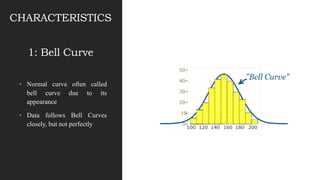
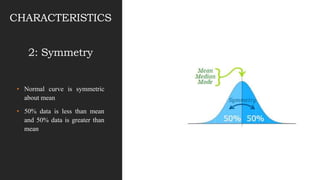
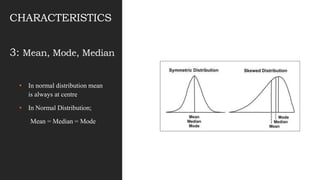
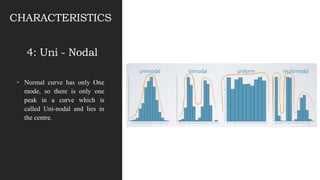
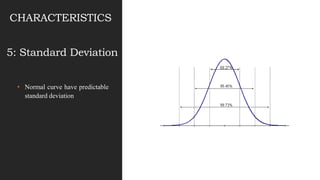
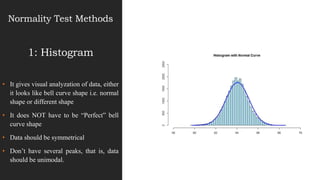
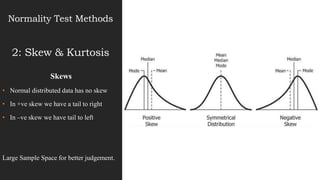
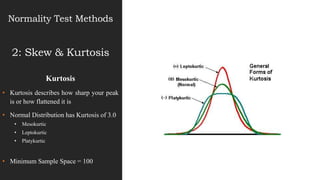
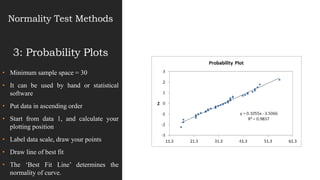
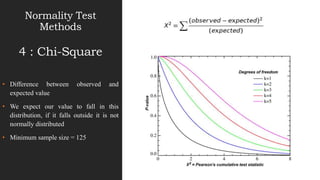
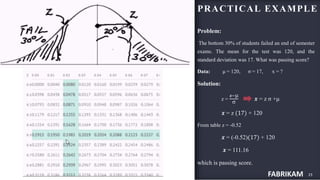
This document discusses normal distribution and normality testing. It defines the normal distribution curve as a bell-shaped curve created by plotting data points that meet the criteria for normal distribution. It provides the mathematical definition of a normal distribution using mean, standard deviation, and the probability density function. It lists key characteristics of the normal distribution curve including its bell shape, symmetry, and that the mean, median, and mode are equal. The document discusses different methods for testing if a data set is normally distributed, including histograms, measures of skew and kurtosis, probability plots, and chi-square goodness of fit tests. It provides an example of how to use the normal distribution and z-scores to calculate a passing score from mean and standard

1. FABRIKAM
METROLOGY & QUALITY ASSURANCE
D e p a r t m e n t o f M e c h a n i c a l E n g i n e e r i n g
UNIVERSITY OF ENGINEERING & TECHNOLOGY LAHORE

2. Normal
Distribution

3. 3
Table of contents
 Normal Distribution Curve
 Non-Normal Distribution
 Mathematical Definition
 Standard Deviation
 Characteristics of Normal Curve
 Normality Test
 Methods for Normality Test
 Example
 Practical Example

4. Normal Distribution Curve
The term “Normal Distribution Curve” is used
to describe the mathematical concept called
normal distribution.
It refers to the shape that is created when a line
is plotted using the data points for an item that
meets the criteria of ‘Normal Distribution’

5. Non-Normal Distribution

6. Mathematical Definition
A continuous random variable X is said to
follow normal distribution with mean ( μ ) and
standard derivation ( σ ), if its probability
function is
f (x) =
1
𝜎 2𝜋
. 𝑒− 𝑥−μ 2
2𝜎2
Where,
μ = mean
σ = Standard deviation

7. Standard Deviation
 The Standard Deviation is a degree of
dispersion from mean value
 It is a measure of how spread out the numbers
are.

8. Characteristics of Normal Distribution
1. Bell Curve
2. Mean, mode and median
3. Symmetry
4. Uni-nodal
5. Standard Deviation
6. The total area under the curve is 1

9. CHARACTERISTICS
1: Bell Curve
• Normal curve often called
bell curve due to its
appearance
• Data follows Bell Curves
closely, but not perfectly

10. • Normal curve is symmetric
about mean
• 50% data is less than mean
and 50% data is greater than
mean
CHARACTERISTICS
2: Symmetry

11. • In normal distribution mean
is always at centre
• In Normal Distribution;
Mean = Median = Mode
CHARACTERISTICS
3: Mean, Mode, Median

12. • Normal curve has only One
mode, so there is only one
peak in a curve which is
called Uni-nodal and lies in
the centre.
CHARACTERISTICS
4: Uni - Nodal

13. • Normal curve have predictable
standard deviation
CHARACTERISTICS
5: Standard Deviation

14. FABRIKAM
NORMALITY
TEST
14

15. Normality Test
Normality tests are used to determine if a data
set is well-modeled by a normal distribution
To compute how likely it is for a random
variable underlying the data set to be normally
distributed.
Need to make sure data is normally distributed
before using a normal distribution

16. FABRIKAM
METHODS FOR
NORMALITY TEST
1. Histogram
2. Skew & Kurtosis
3. Probability Plots
4. Chi-Square goodness of Fit
16

17. Normality Test Methods
1: Histogram
• It gives visual analyzation of data, either
it looks like bell curve shape i.e. normal
shape or different shape
• It does NOT have to be “Perfect” bell
curve shape
• Data should be symmetrical
• Don’t have several peaks, that is, data
should be unimodal.

18. Normality Test Methods
2: Skew & Kurtosis
Skews
• Normal distributed data has no skew
• In +ve skew we have a tail to right
• In –ve skew we have tail to left
Large Sample Space for better judgement.

19. Normality Test Methods
2: Skew & Kurtosis
Kurtosis
• Kurtosis describes how sharp your peak
is or how flattened it is
• Normal Distribution has Kurtosis of 3.0
• Mesokurtic
• Leptokurtic
• Platykurtic
• Minimum Sample Space = 100

20. Normality Test Methods
3: Probability Plots
• Minimum sample space = 30
• It can be used by hand or statistical
software
• Put data in ascending order
• Start from data 1, and calculate your
plotting position
• Label data scale, draw your points
• Draw line of best fit
• The ‘Best Fit Line’ determines the
normality of curve.

21. Normality Test
Methods
4 : Chi-Square
• Difference between observed and
expected value
• We expect our value to fall in this
distribution, if it falls outside it is not
normally distributed
• Minimum sample size = 125

22. Examples of Normal Distribution
• Height of people
• Measurement errors
• Blood pressure
• Point on a test
• IQ score
• Salaries

23. FABRIKAMFABRIKAM
PRACTICAL EXAMPLE
Problem:
The bottom 30% of students failed an end of semester
exams. The mean for the test was 120, and the
standard deviation was 17. What was passing score?
Data: μ = 120, σ = 17, x = ?
Solution:
z =
𝒙−μ
σ
𝒙 = z σ +μ
𝒙 = z (17) + 120
From table z = -0.52
𝒙 = (-0.52)(17) + 120
𝒙 = 111.16
which is passing score.
23