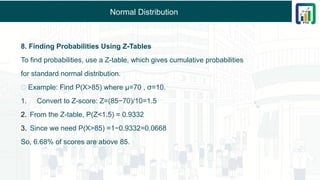
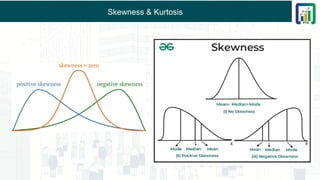
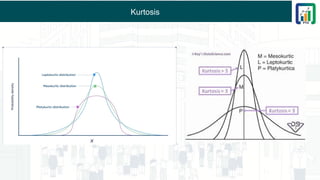
Section 6 - Chapter 3 - Introduction to Probablity - Presented by Rohan Sharma - The CMT Coach - Chartered Market Technician CMT Level 1 Study Material - CMT Level 1 Chapter Wise Short Notes - CMT Level 1 Course Content - CMT Level 1 2025 Exam Syllabus Visit Site : www.learn.ptaindia.com and www.ptaindia.com