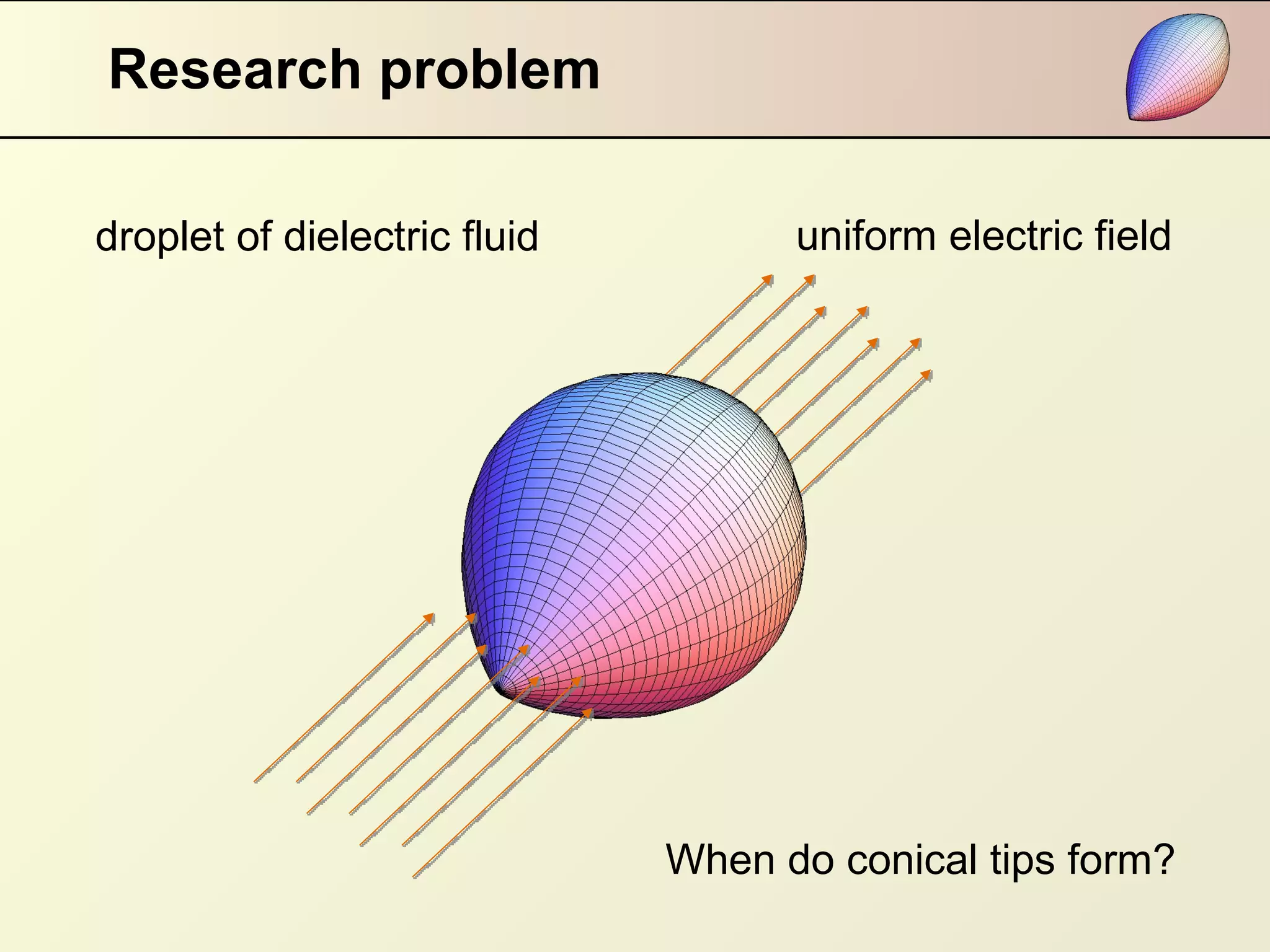
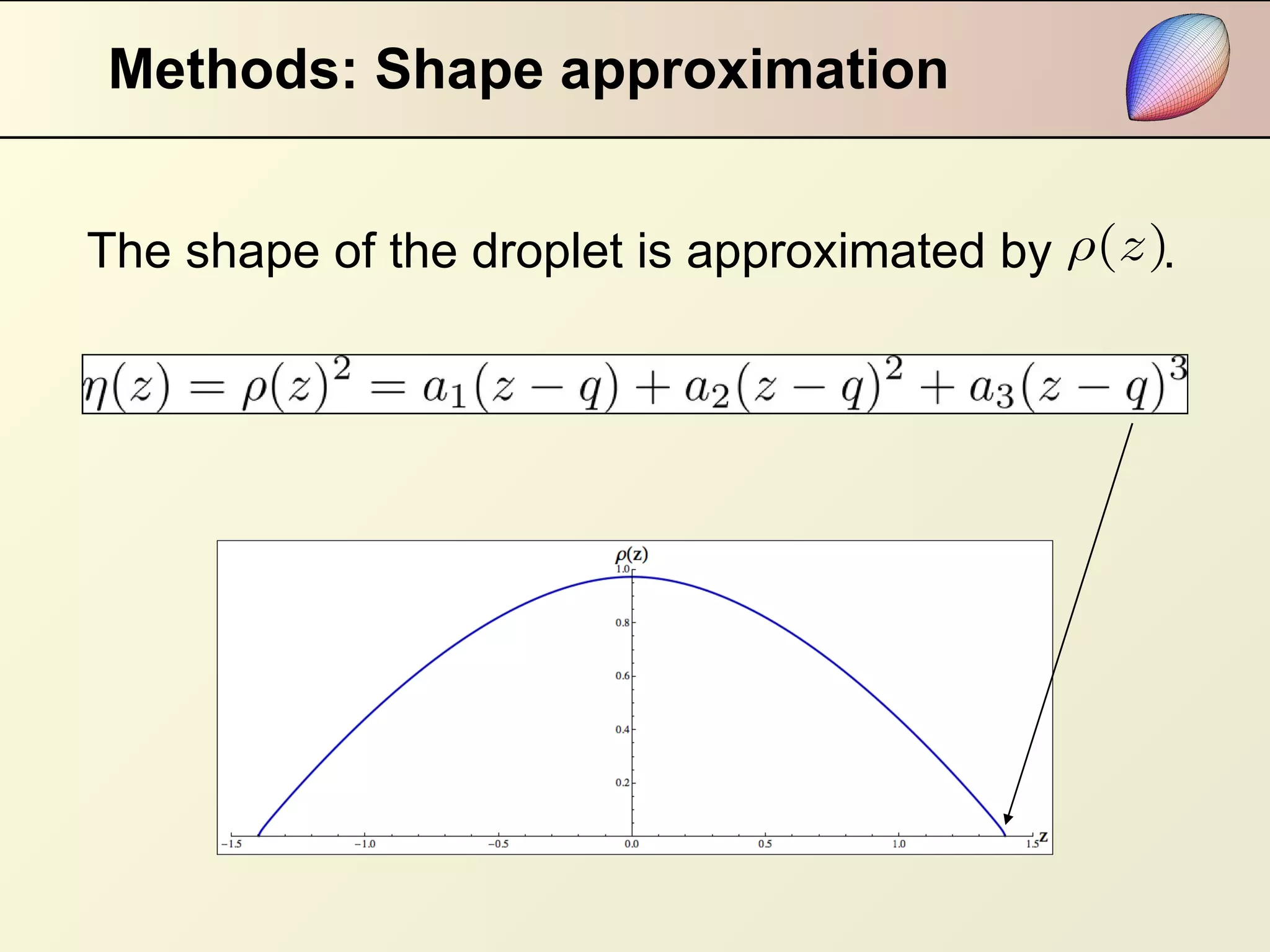
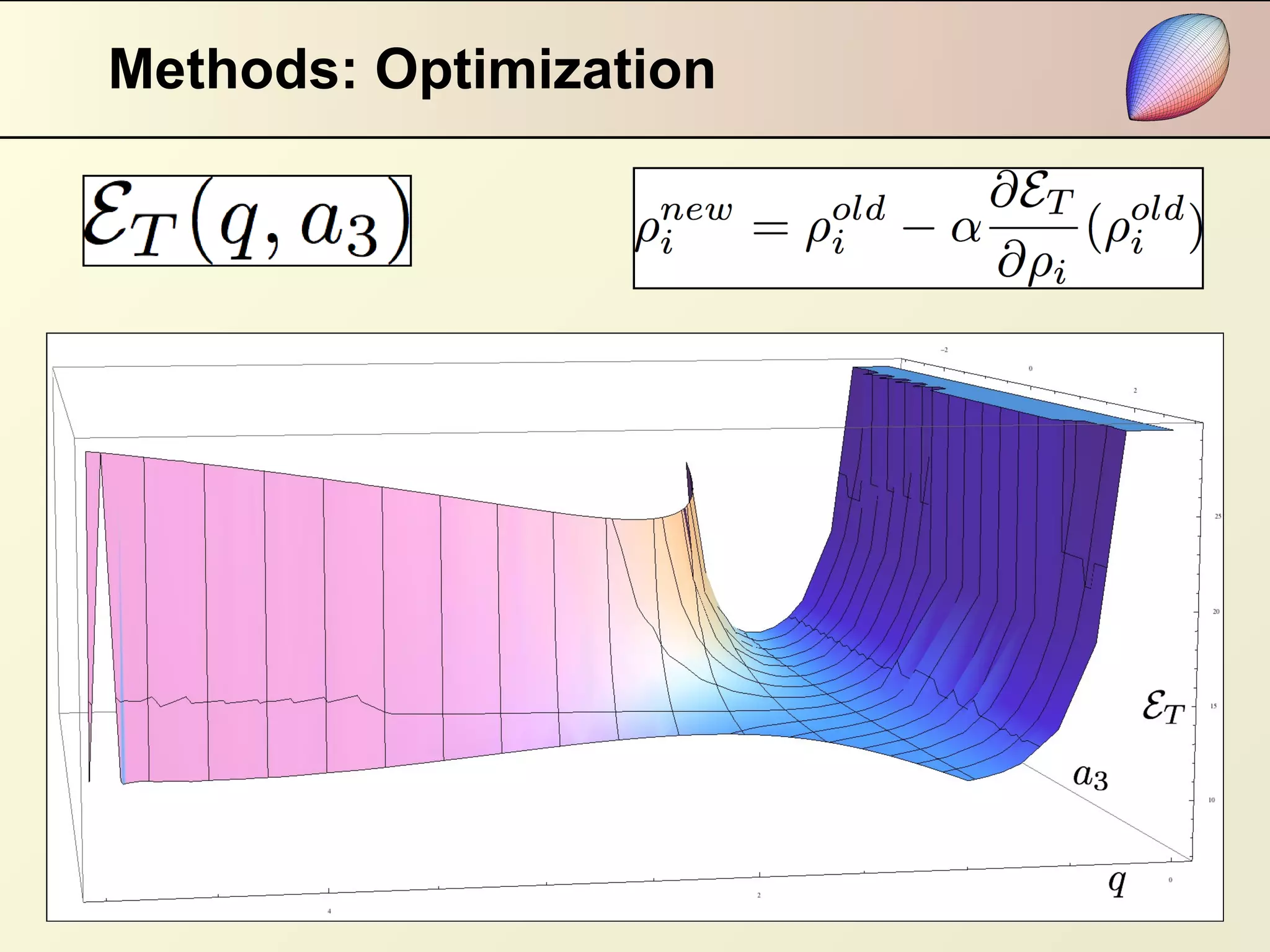
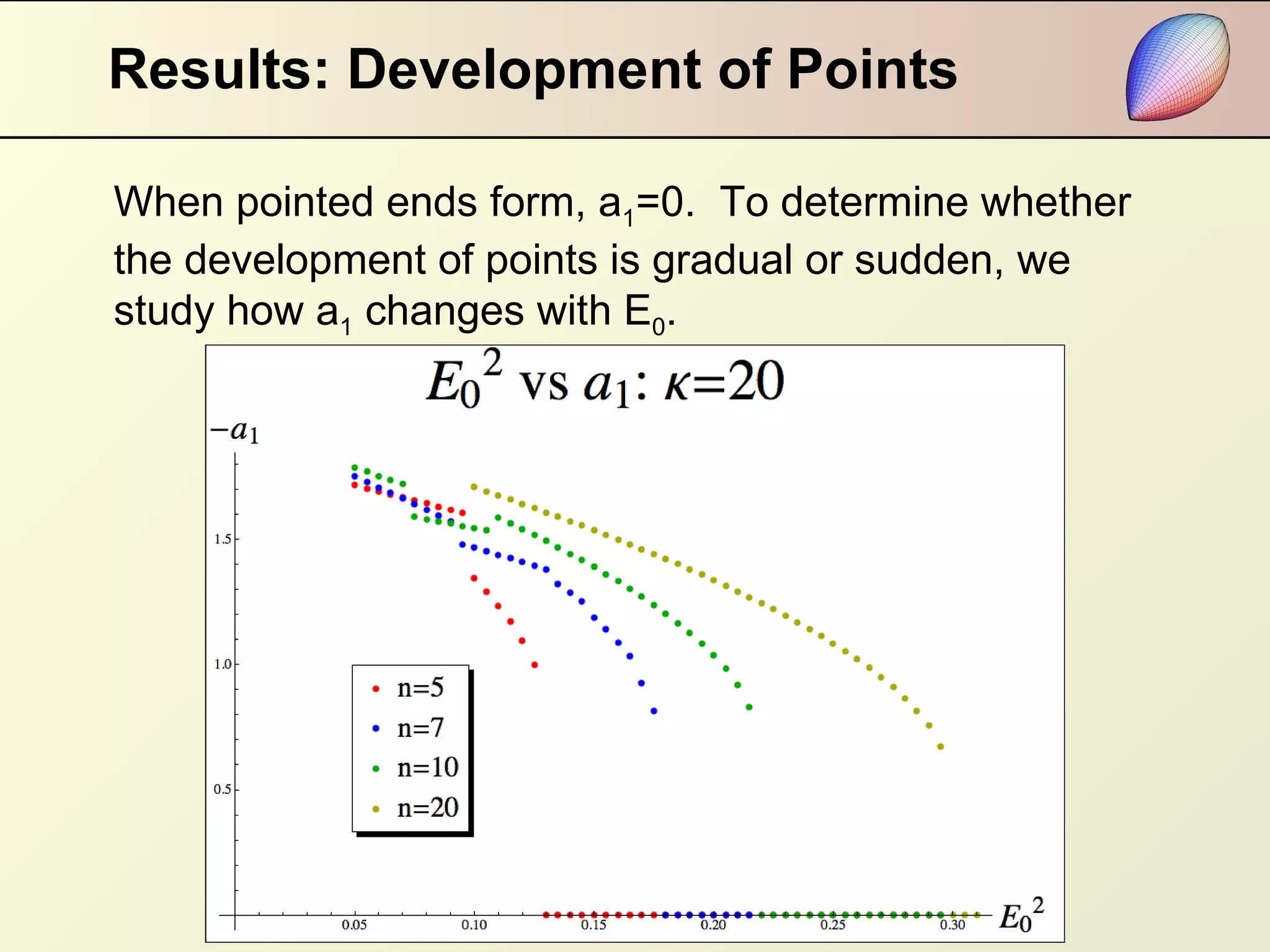
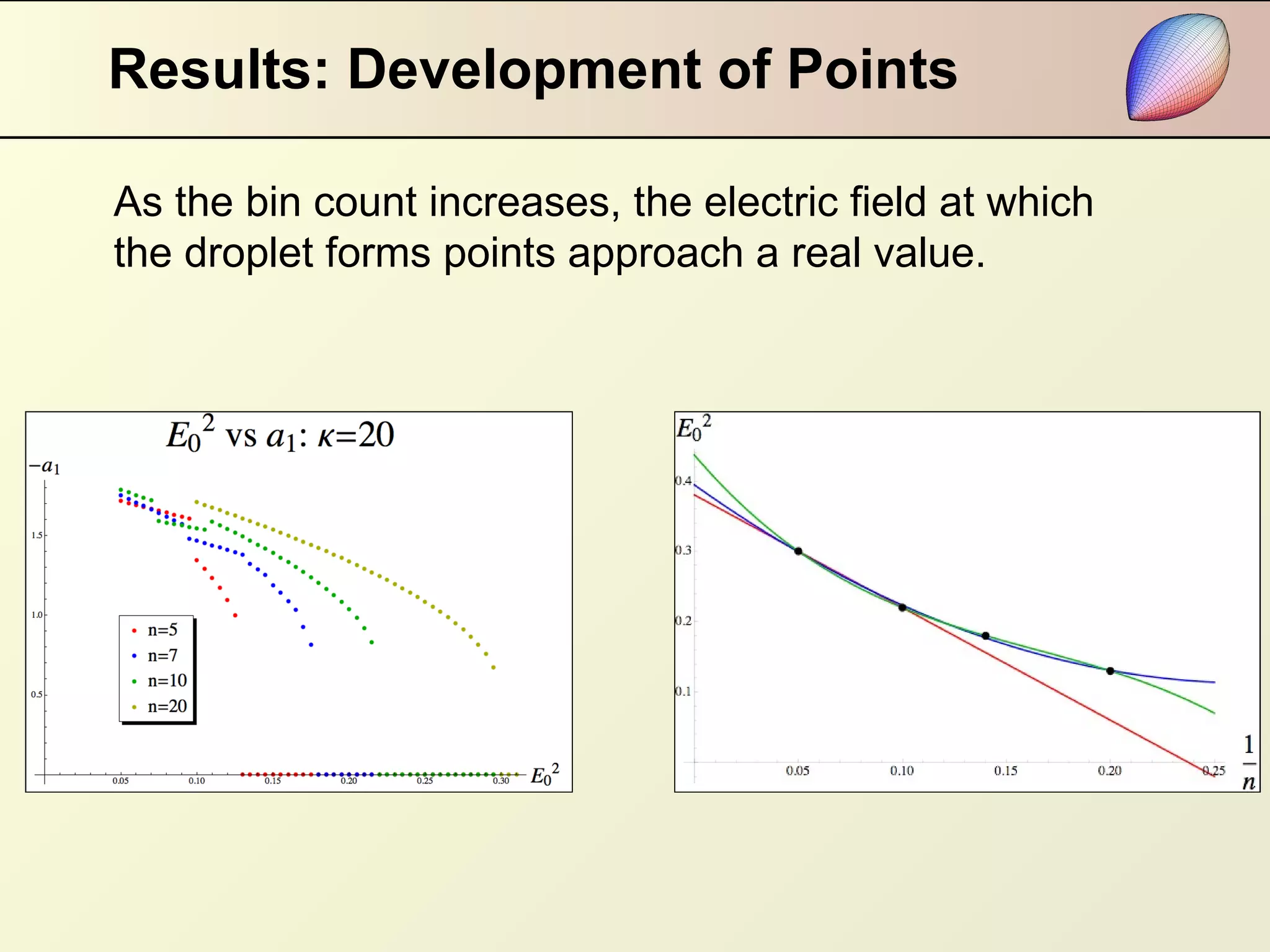
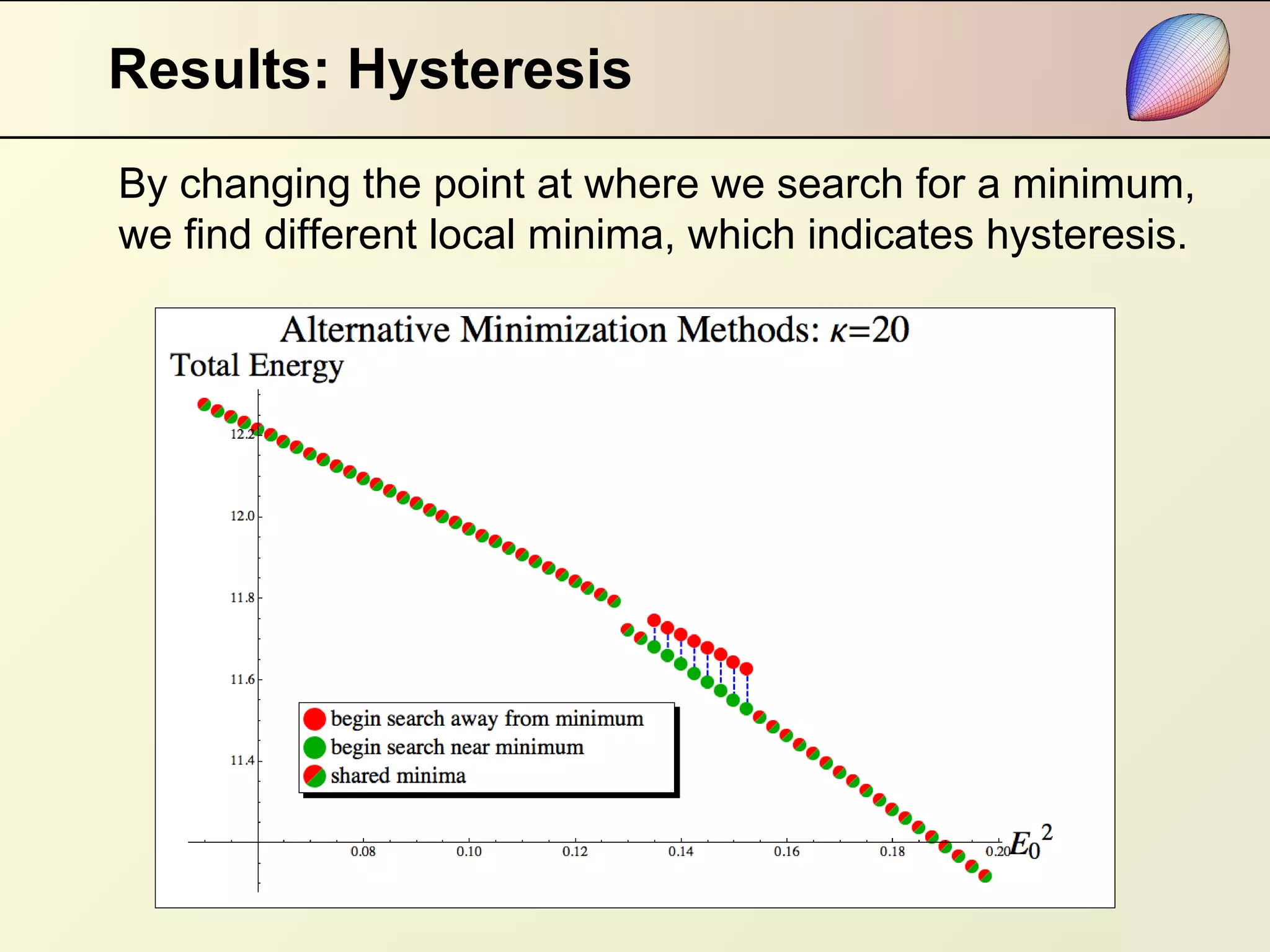
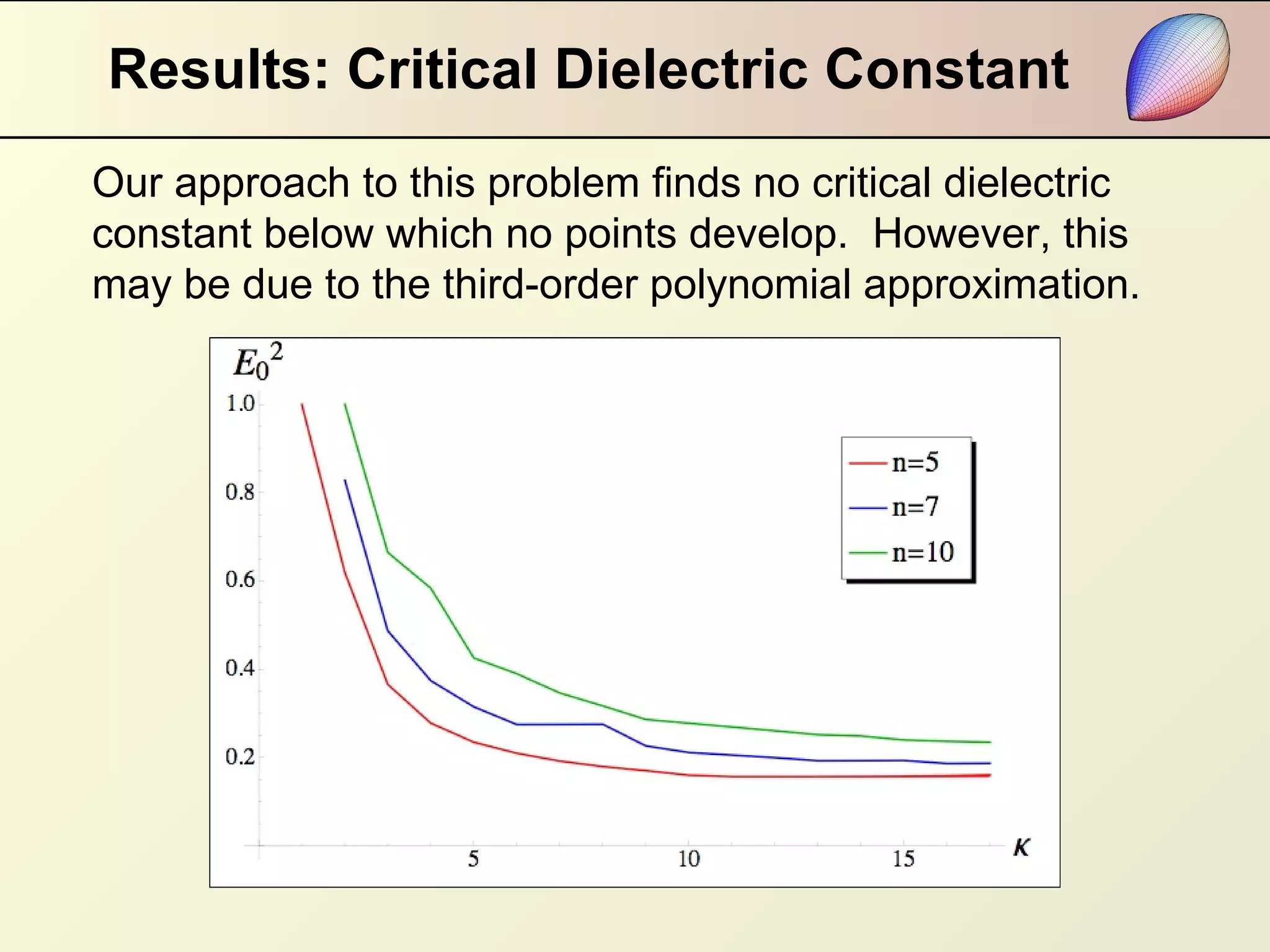
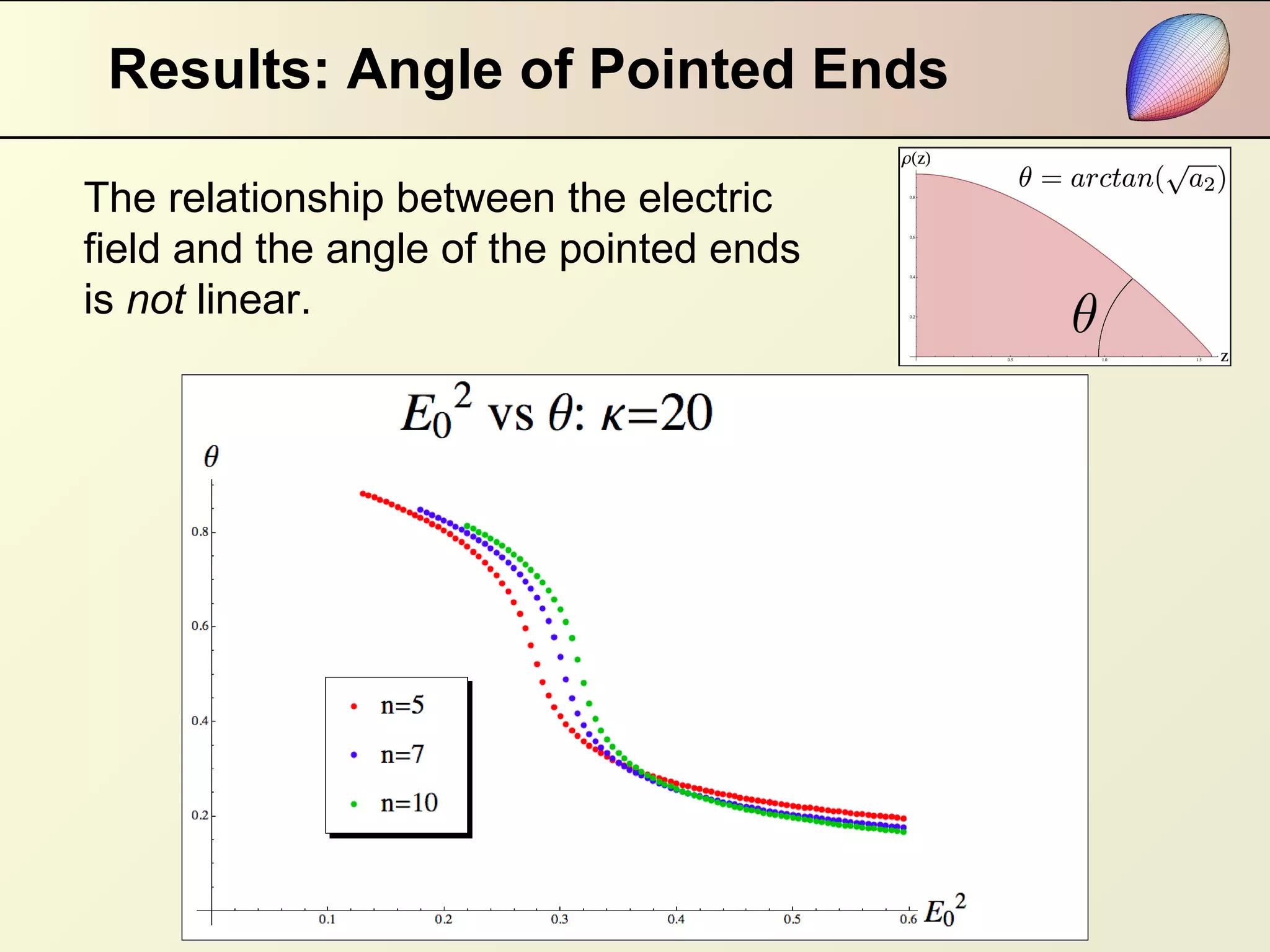
This document summarizes research on modeling the equilibrium shape of a dielectric droplet placed in a uniform electric field. The researchers used a third-order polynomial approximation to represent the shape of the droplet and calculated the total energy as a function of surface energy and electrostatic energy. They were able to determine the shape of the droplet for given dielectric properties and electric field strength. Their results showed that pointed ends develop when a parameter reaches zero, and there is hysteresis in the system depending on the starting point of the energy minimization calculation. The relationship between electric field strength and the angle of pointed ends was found to be nonlinear.

1. Equilibrium shape of a dielectric droplet in an electric field Nicholas Goble - Illinois Wesleyan University Dr. Philip Taylor - Case Western Reserve University

2. Research problem droplet of dielectric fluid

3. Research problem droplet of dielectric fluid uniform electric field When do conical tips form?

4. Methods: Shape approximation The shape of the droplet is approximated by .

5. Methods: Energy calculation Total Energy = Surface Energy Electrostatic Energy +

6. Methods: Energy calculation Total Energy = Surface Energy Electrostatic Energy + Surface Energy Volume Surface Energy Density = x

7. Methods: Energy calculation Total Energy = Surface Energy Electrostatic Energy + Surface Energy Volume Surface Energy Density = x

8. Methods: Optimization

9. Results: Shape of Droplet For a given dielectric constant and electric field, we are able to find the shape of the droplet.

10. Results: Development of Points When pointed ends form, a 1 =0. To determine whether the development of points is gradual or sudden, we study how a 1 changes with E 0 .

11. Results: Development of Points As the bin count increases, the electric field at which the droplet forms points approach a real value.

12. Results: Development of Points

13. Results: Hysteresis By changing the point at where we search for a minimum, we find different local minima, which indicates hysteresis.

14. Results: Critical Dielectric Constant Our approach to this problem finds no critical dielectric constant below which no points develop. However, this may be due to the third-order polynomial approximation.

15. Results: Angle of Pointed Ends The relationship between the electric field and the angle of the pointed ends is not linear.

16. Conclusion Our methods have given us an expression for a dielectric droplet in an electric field. Future goals include using a fourth-order polynomial in hopes of finding a critical dielectric constant. We are also able to explore the angle of the points, hysteresis, and the formation of conical tips.

17. NSF CWRU Physics Department Dr. Philip Taylor Gareth Kafka Acknowledgements: