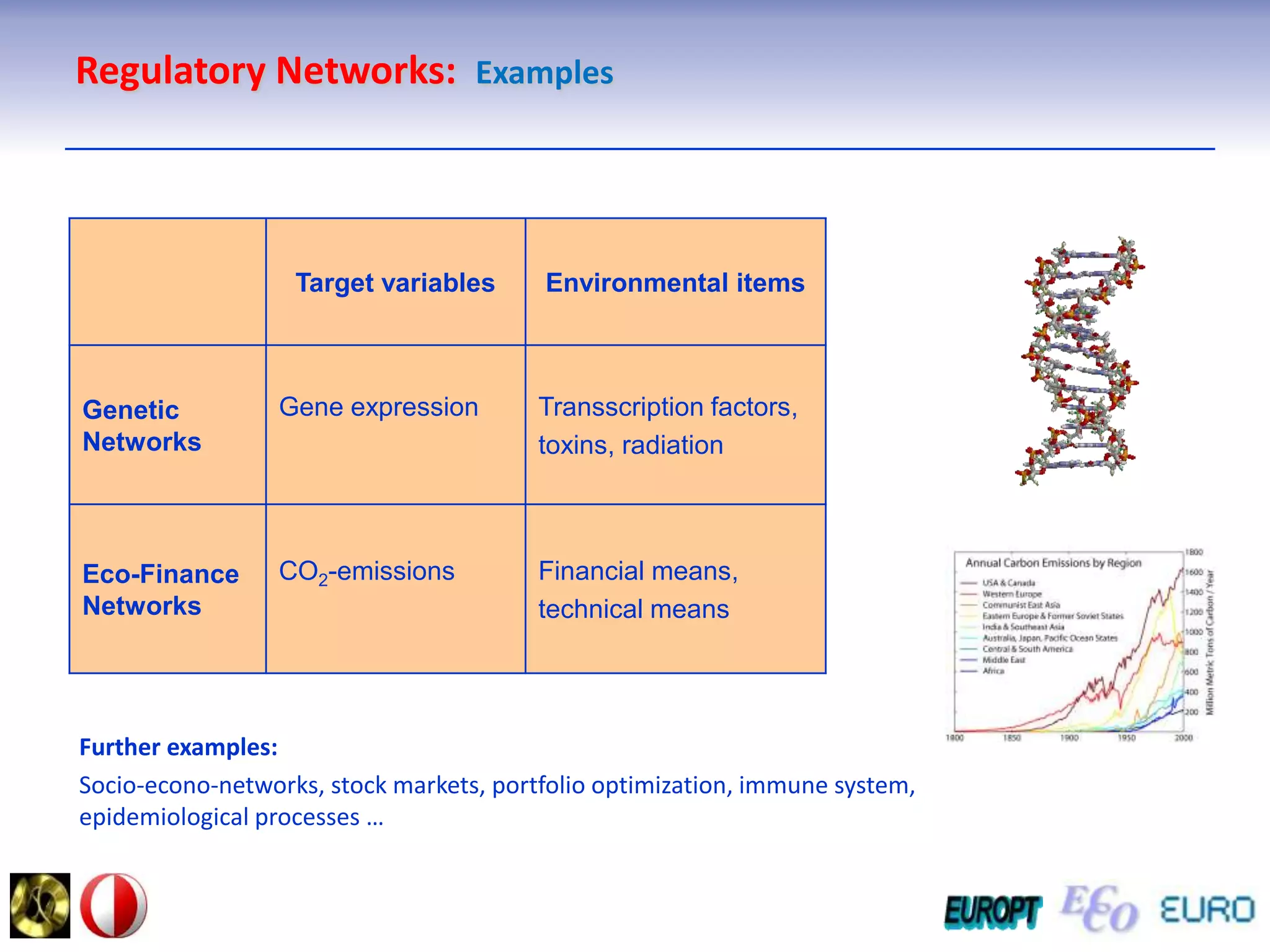
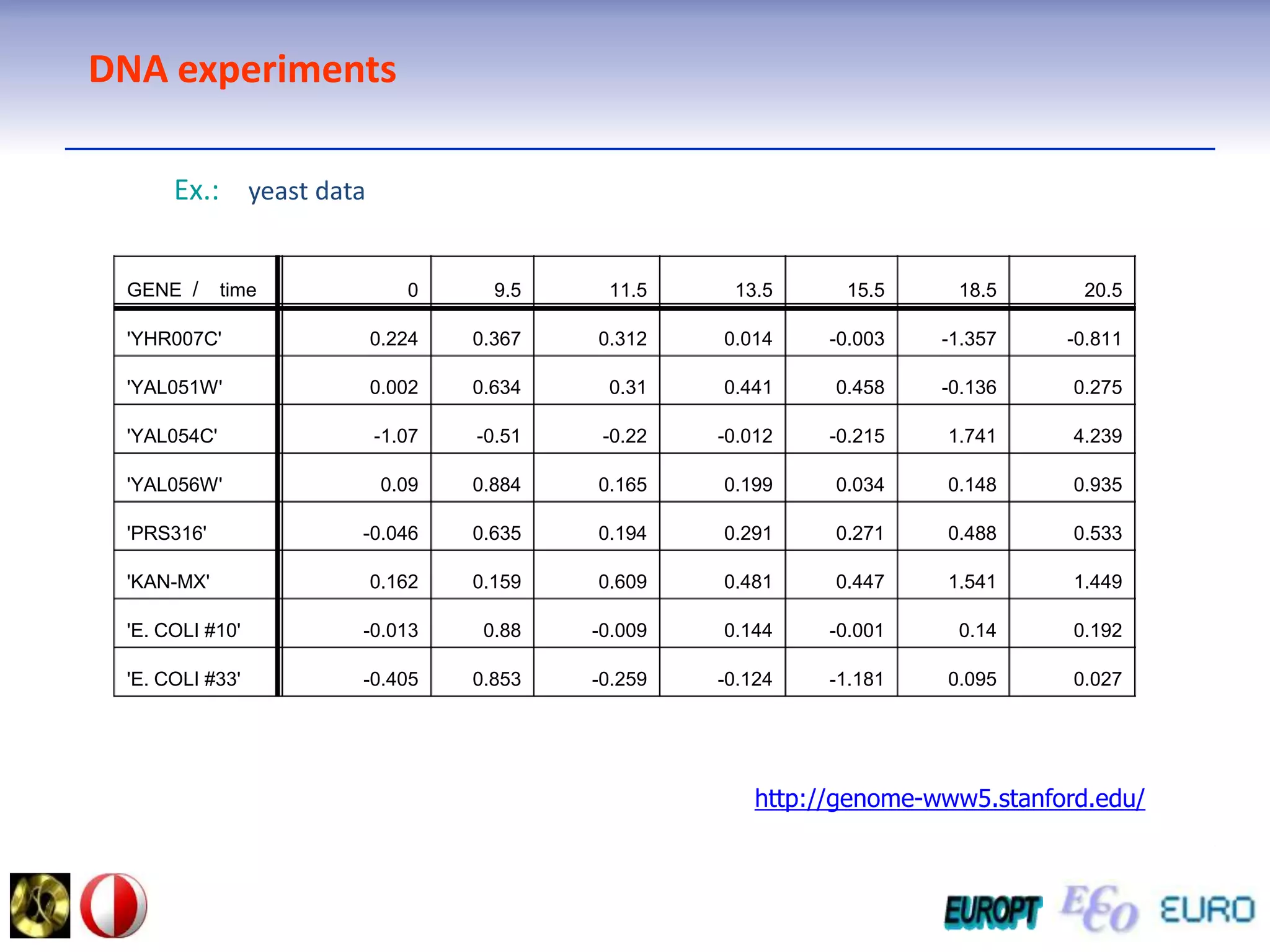
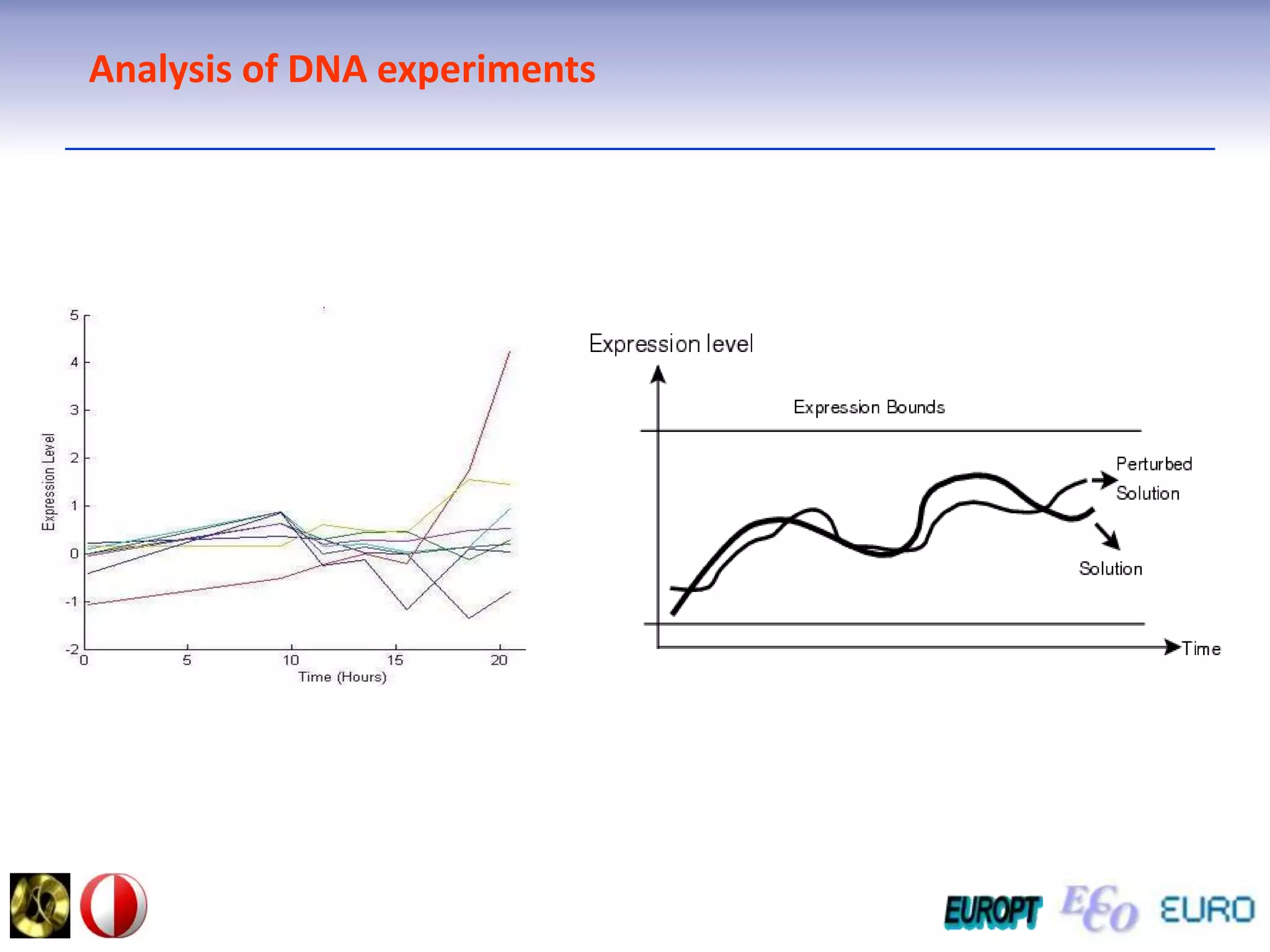
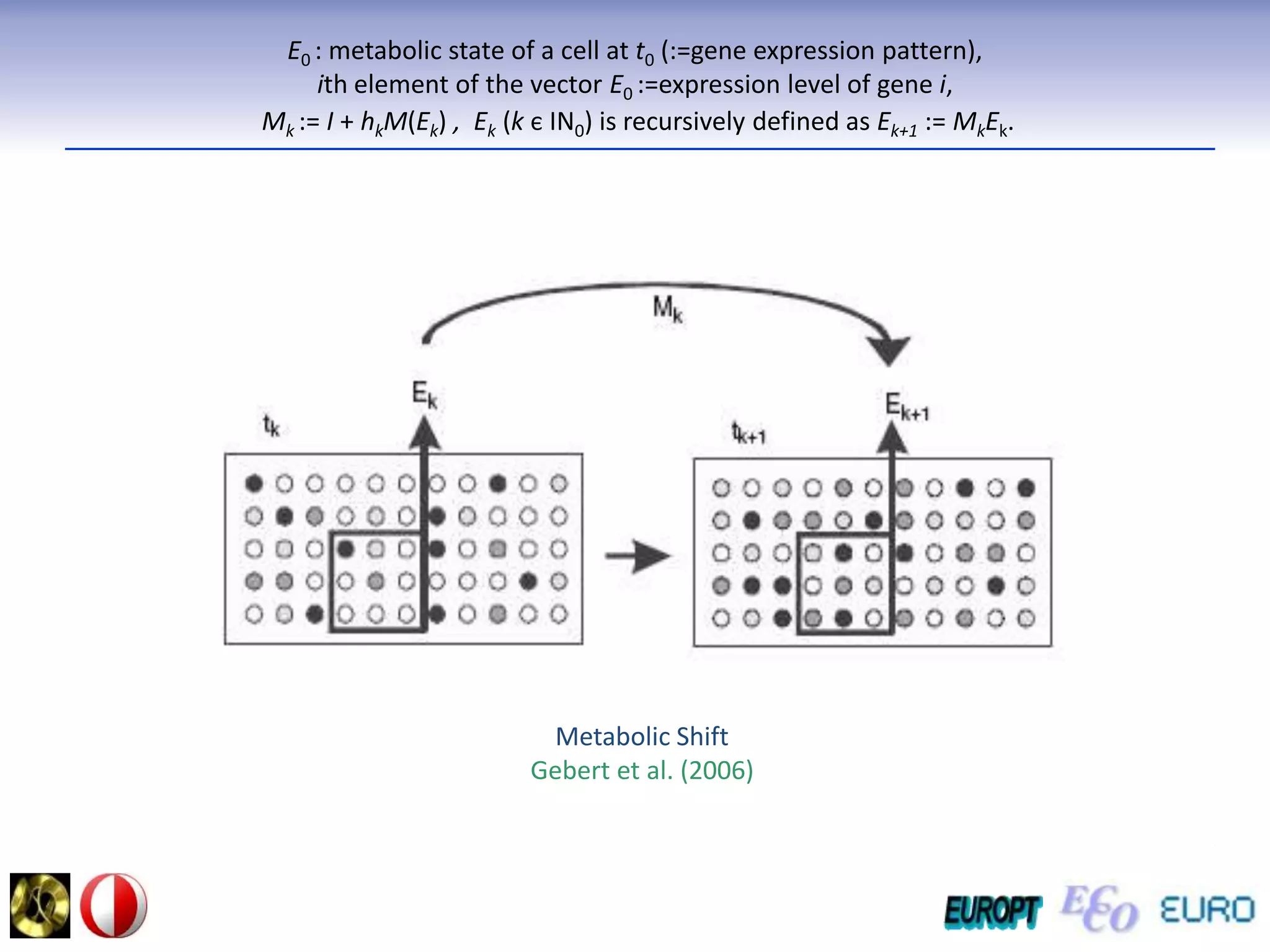
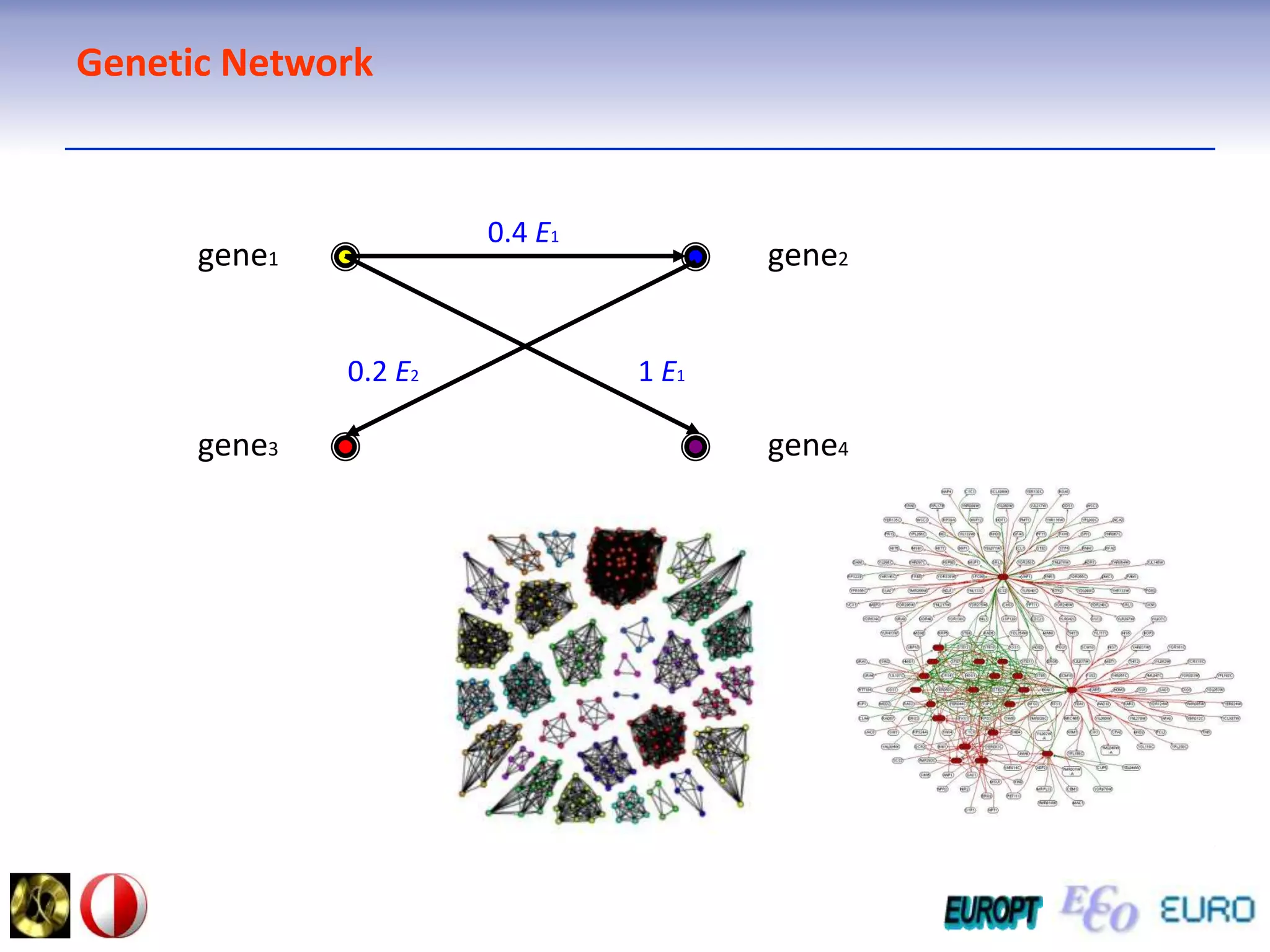
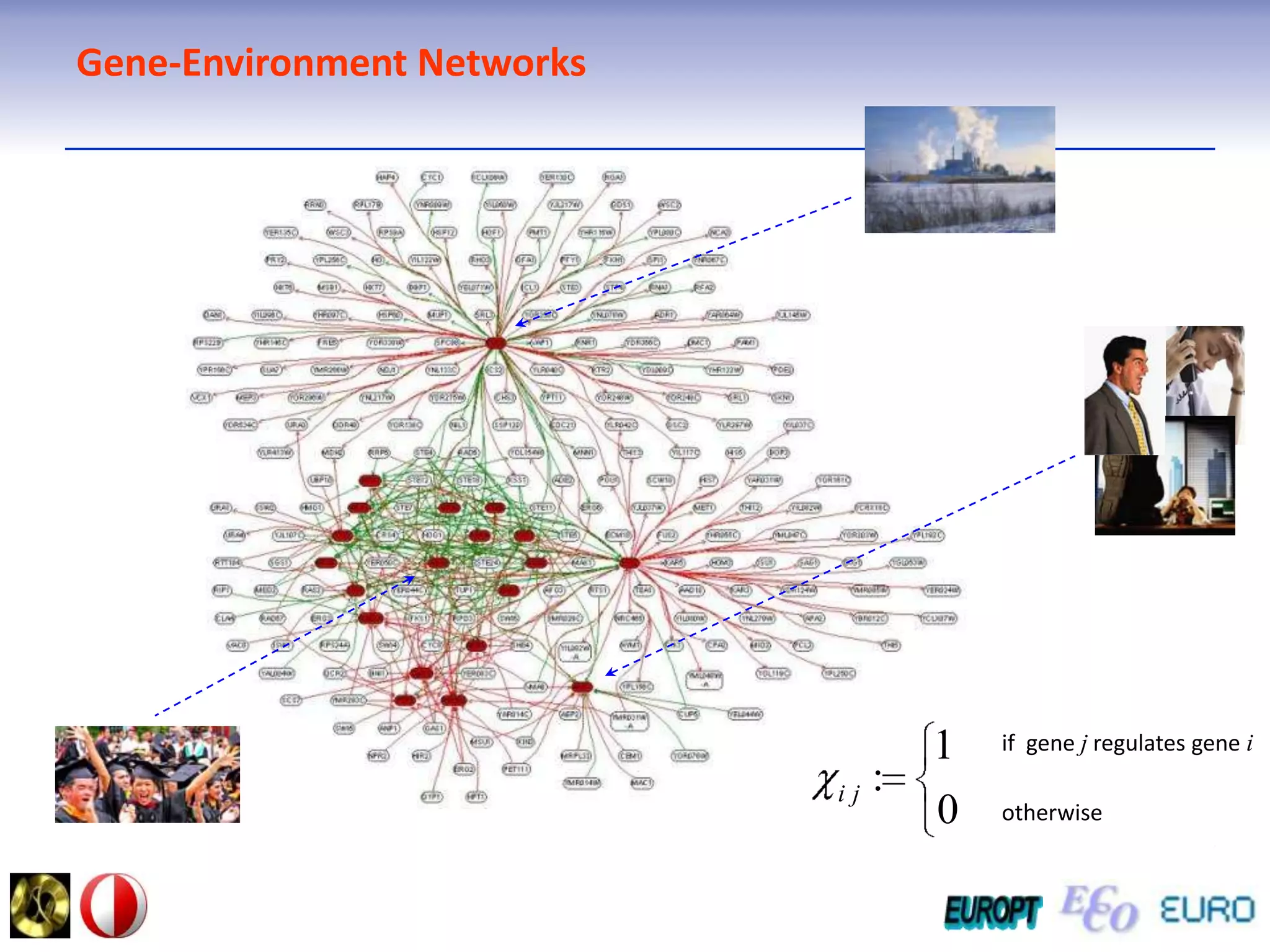
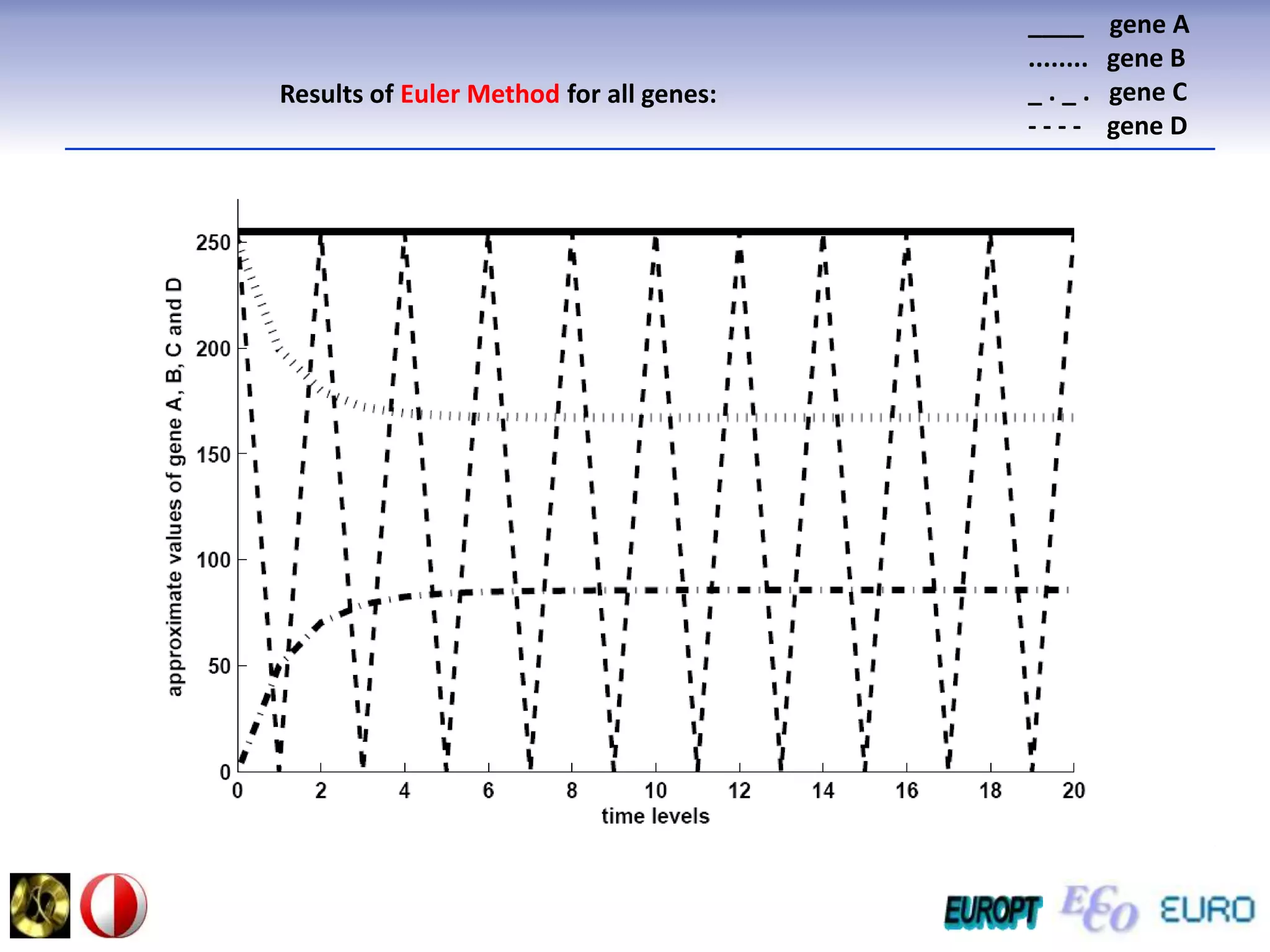
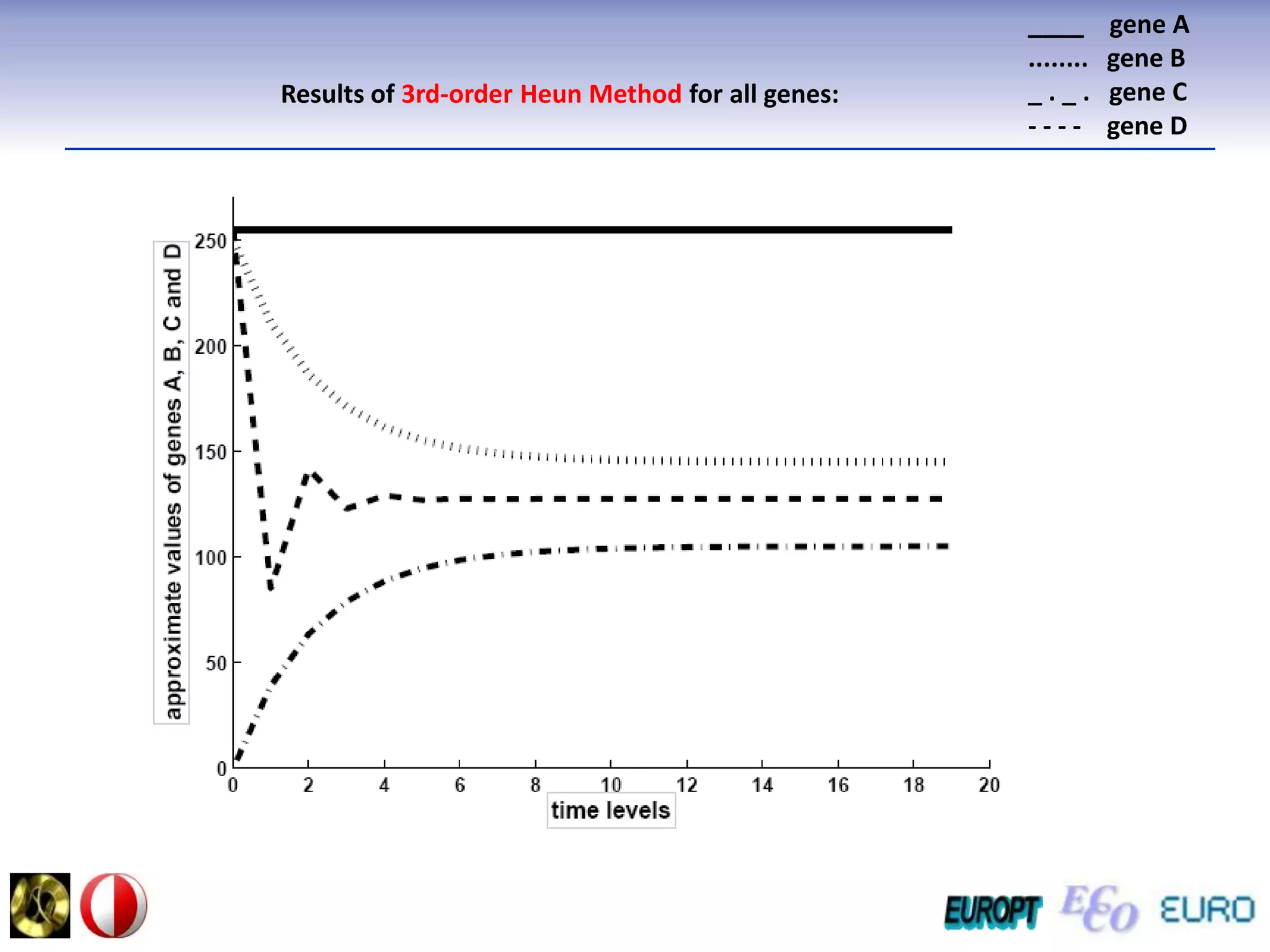
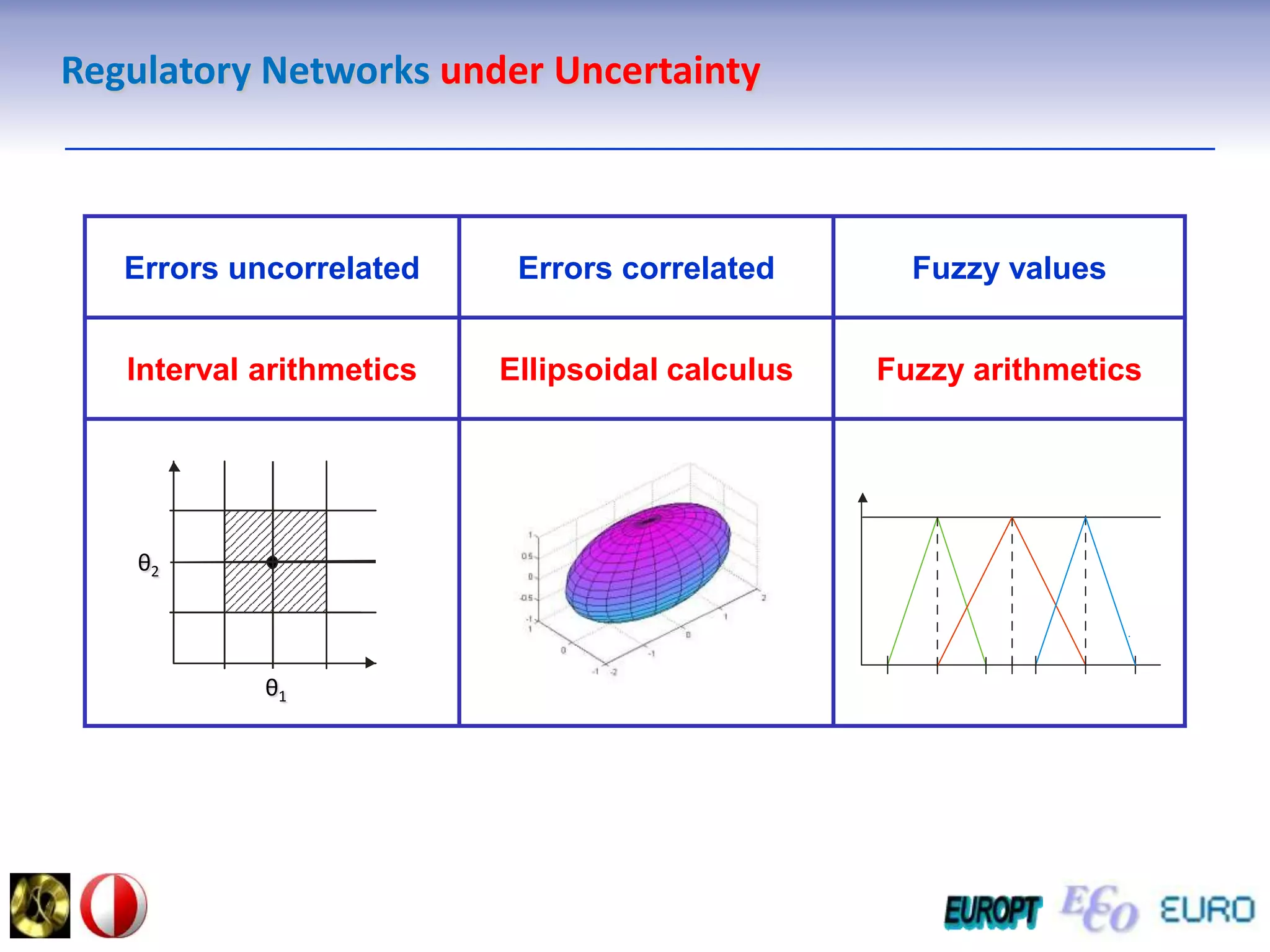
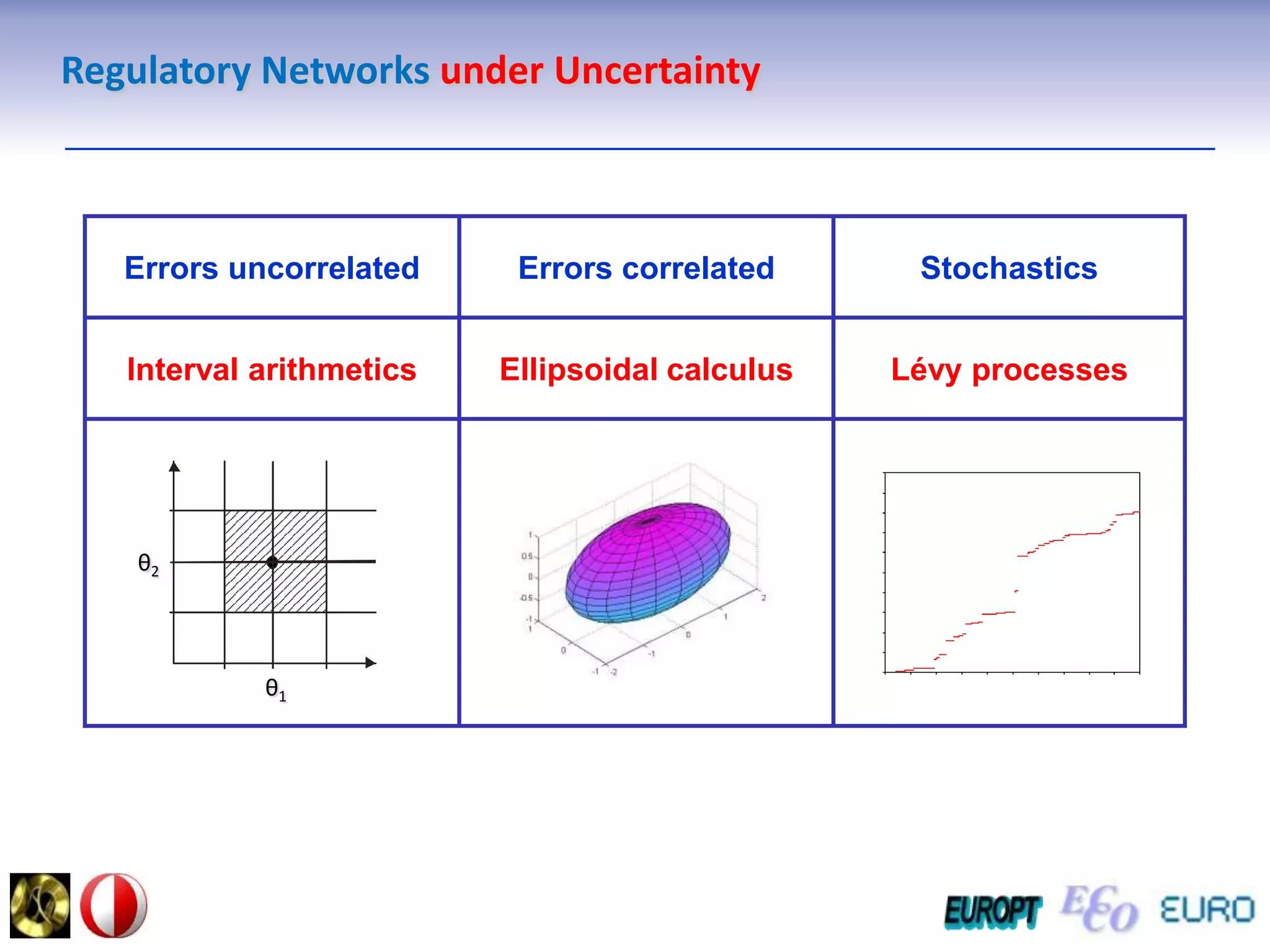
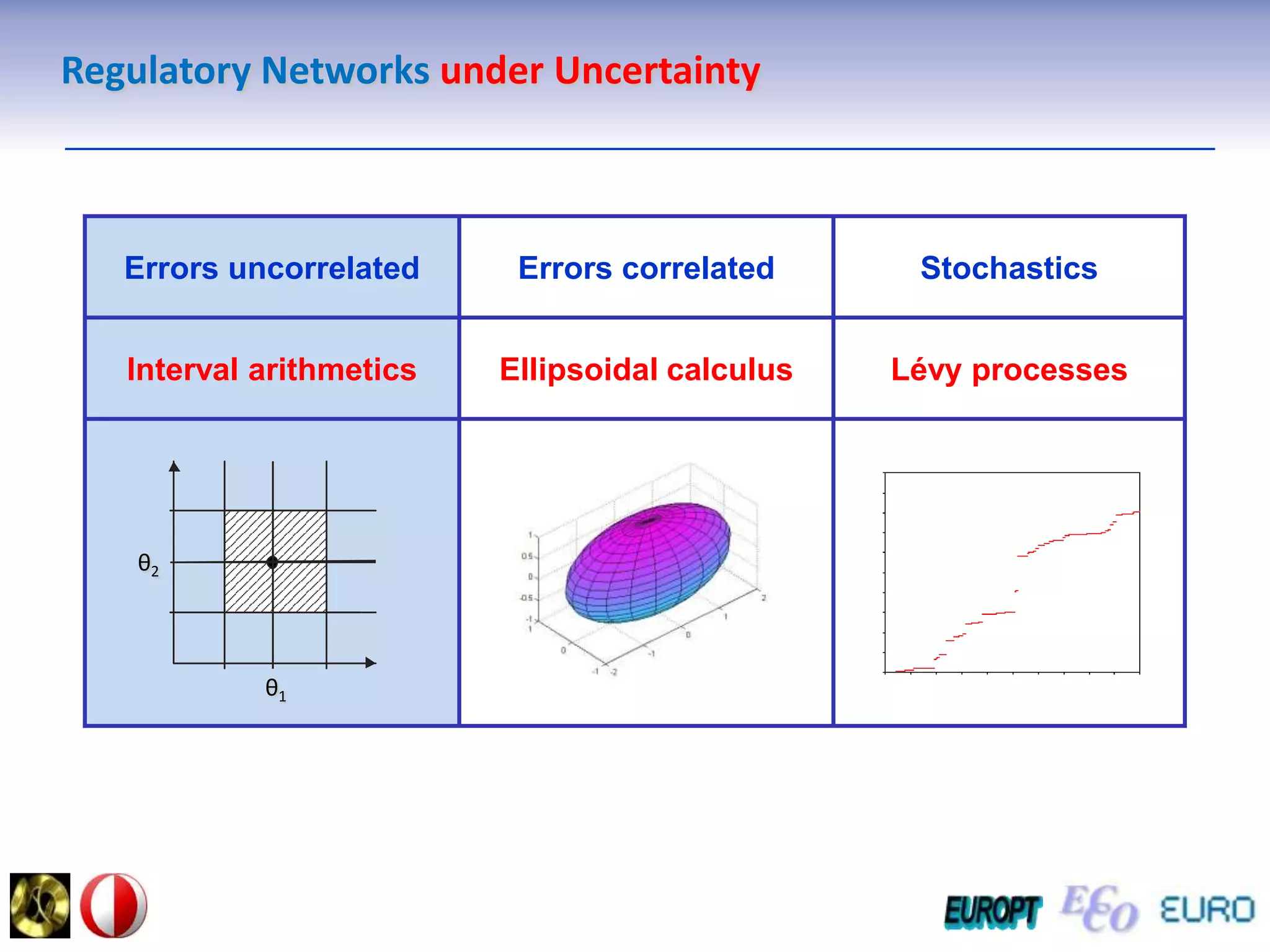
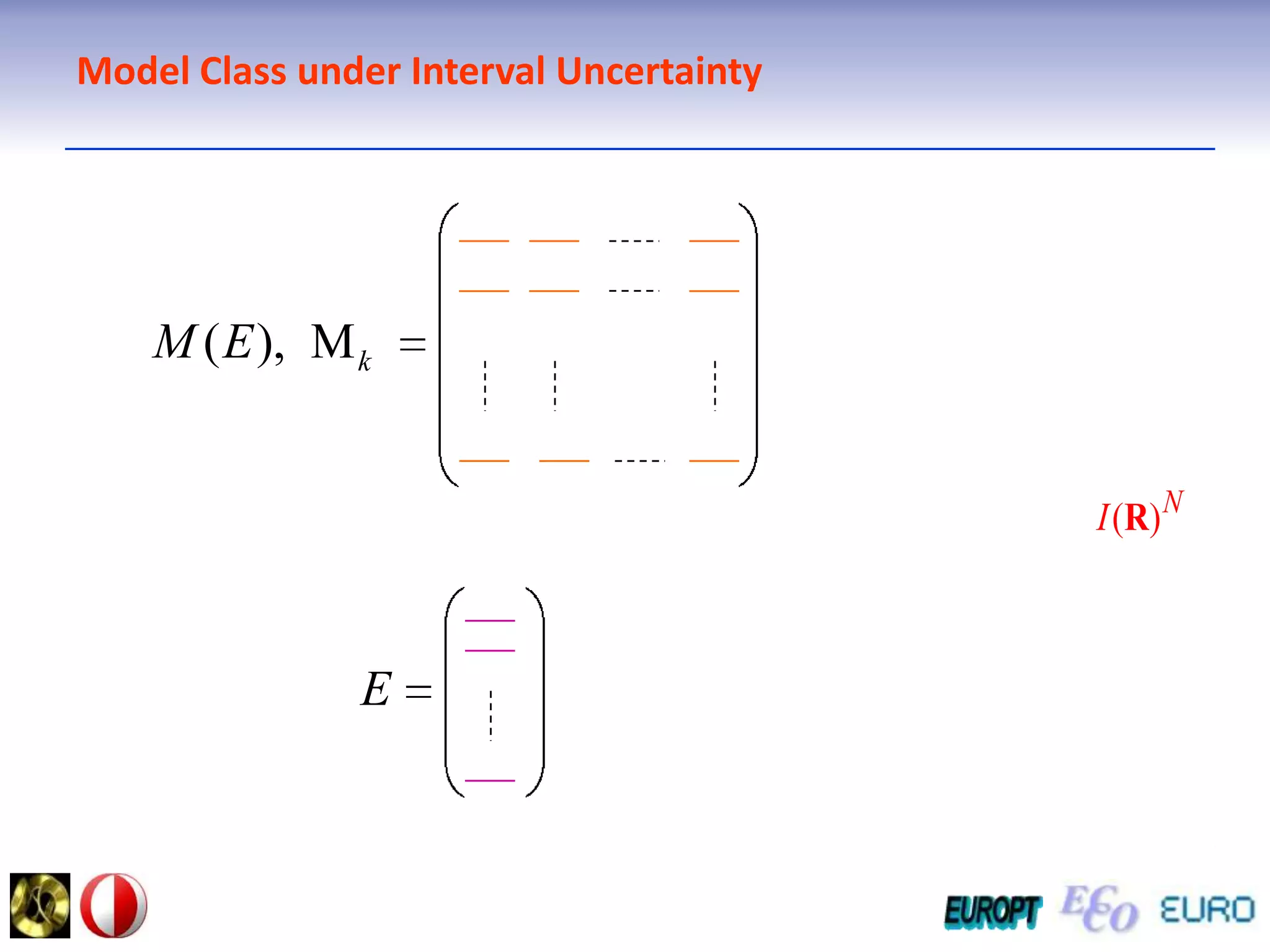
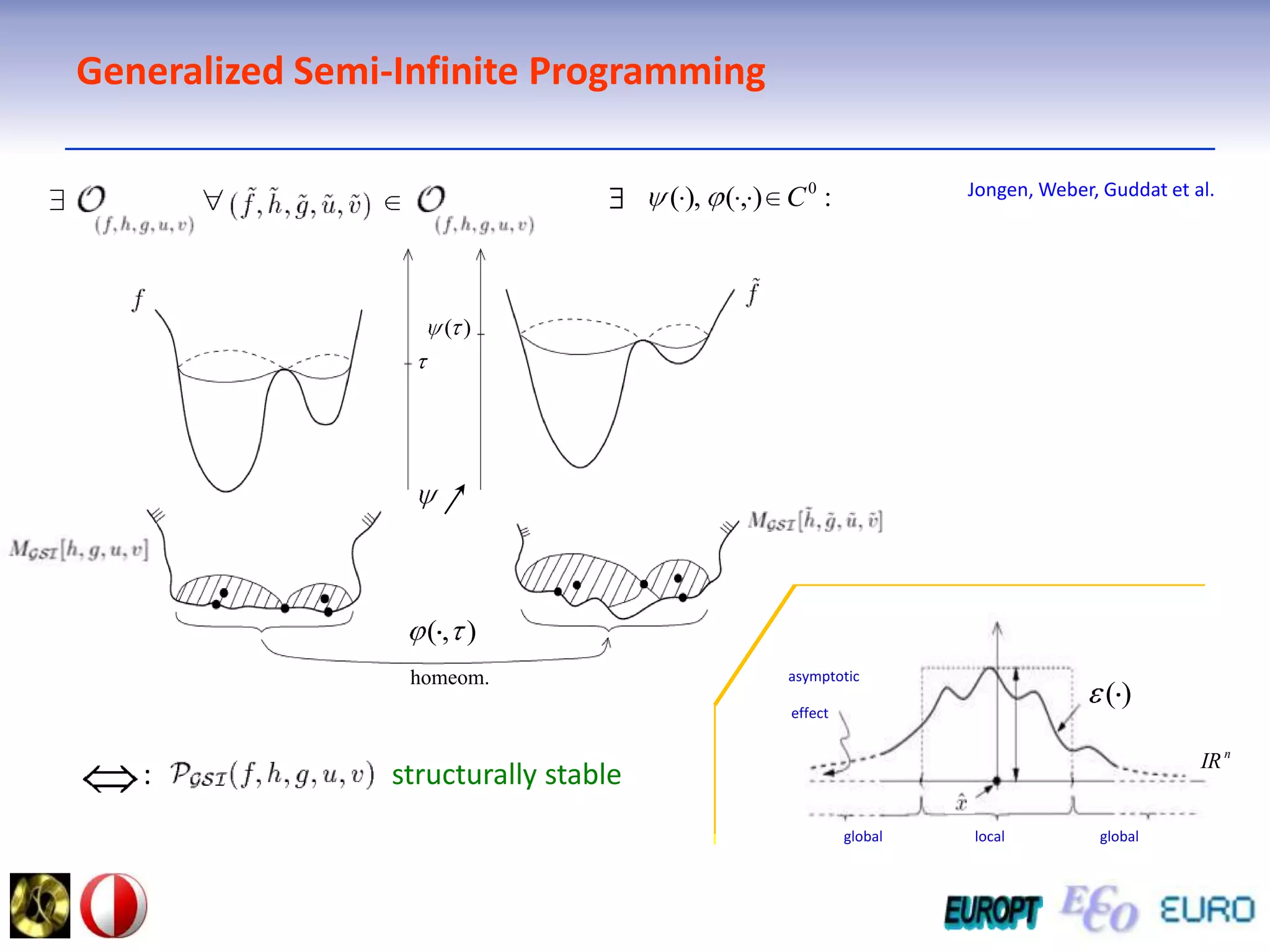
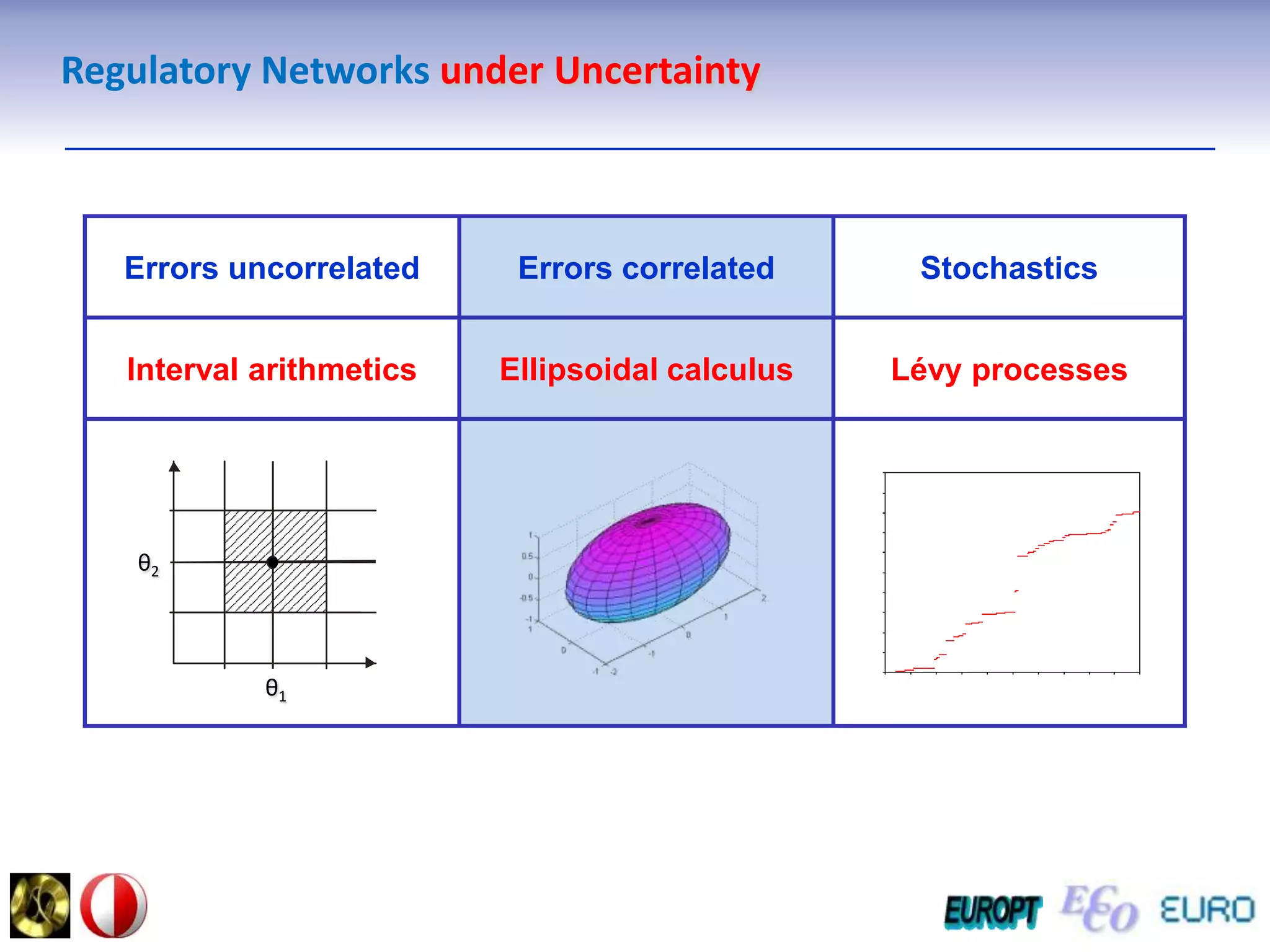
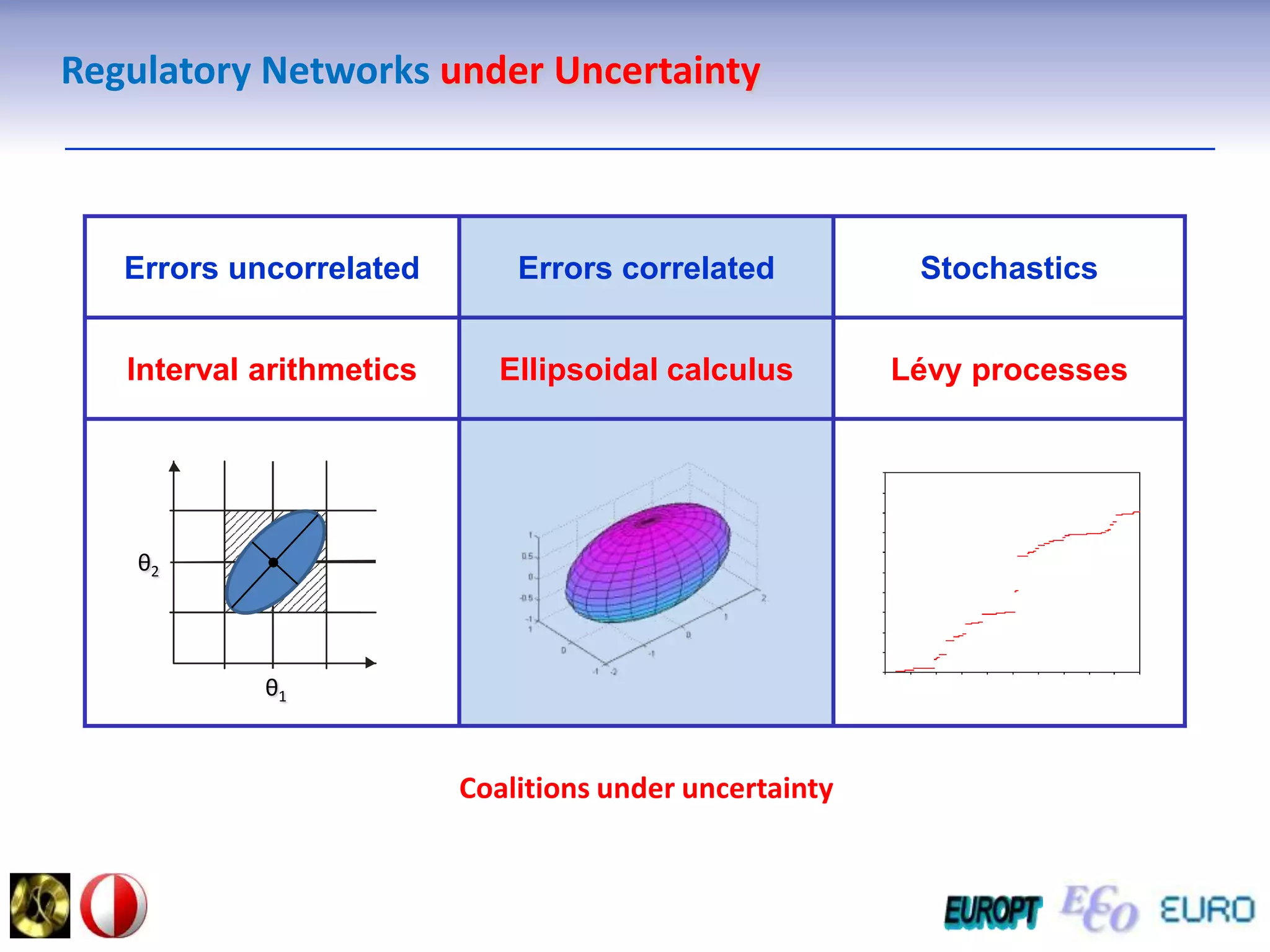
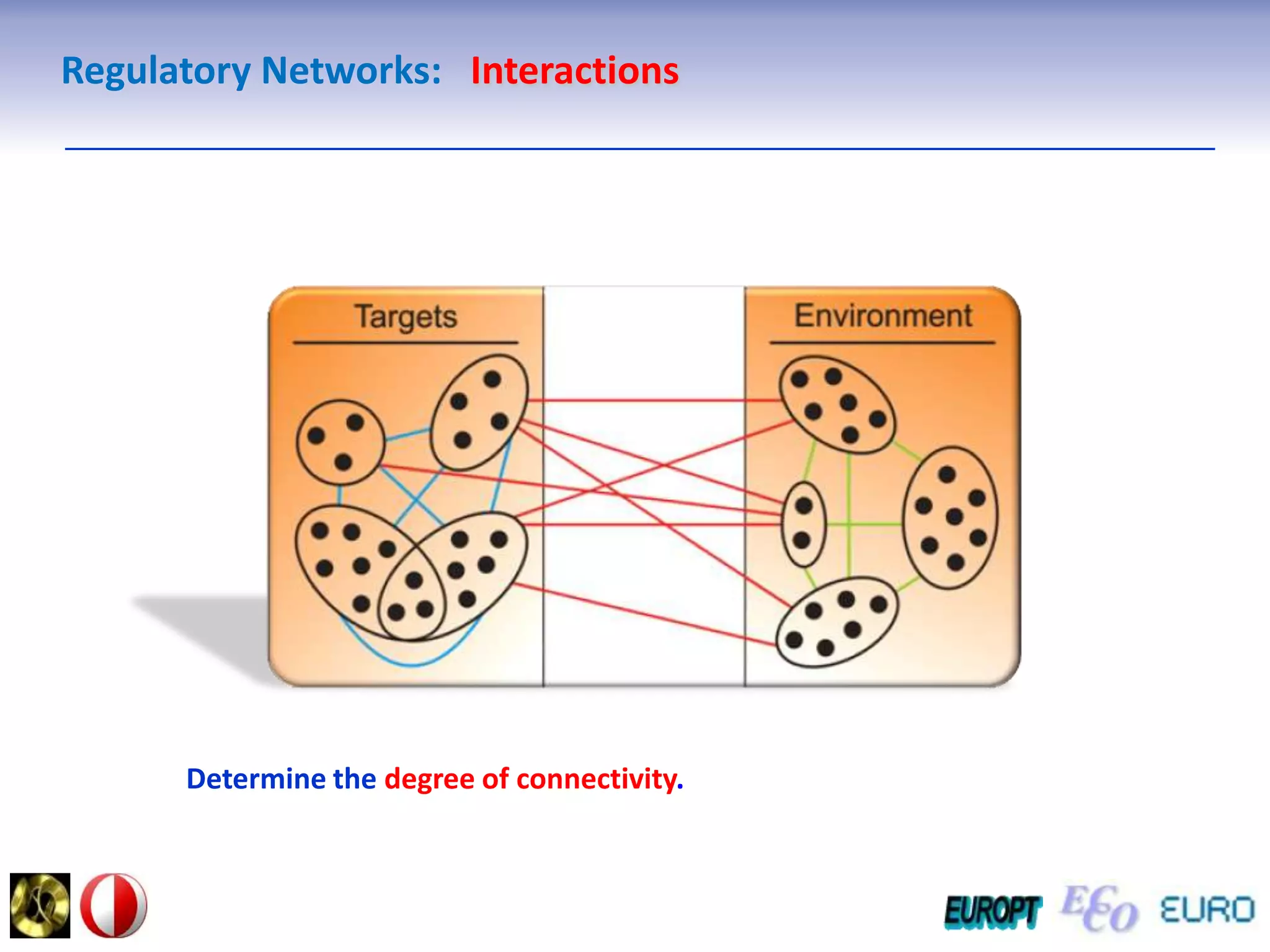
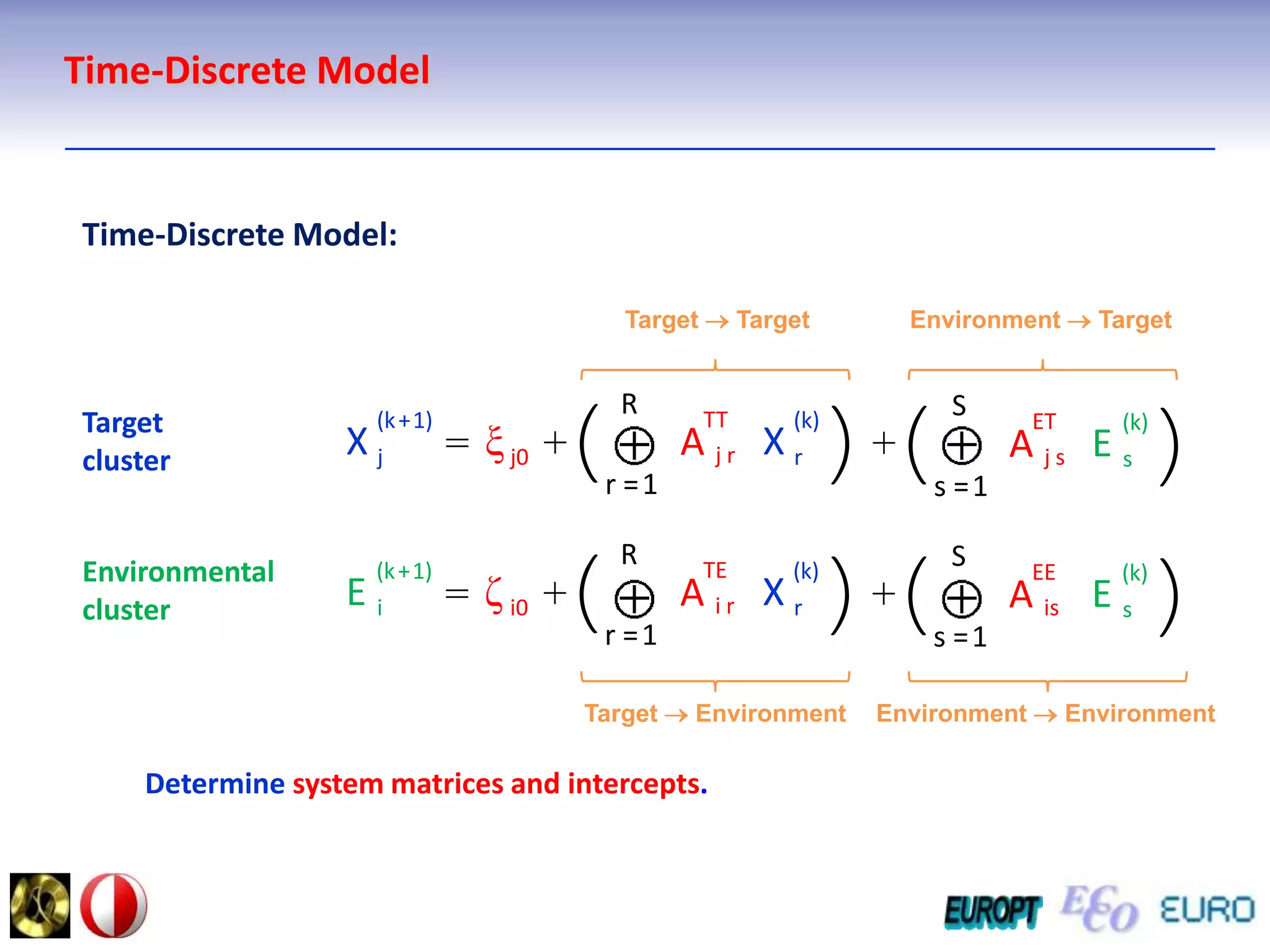
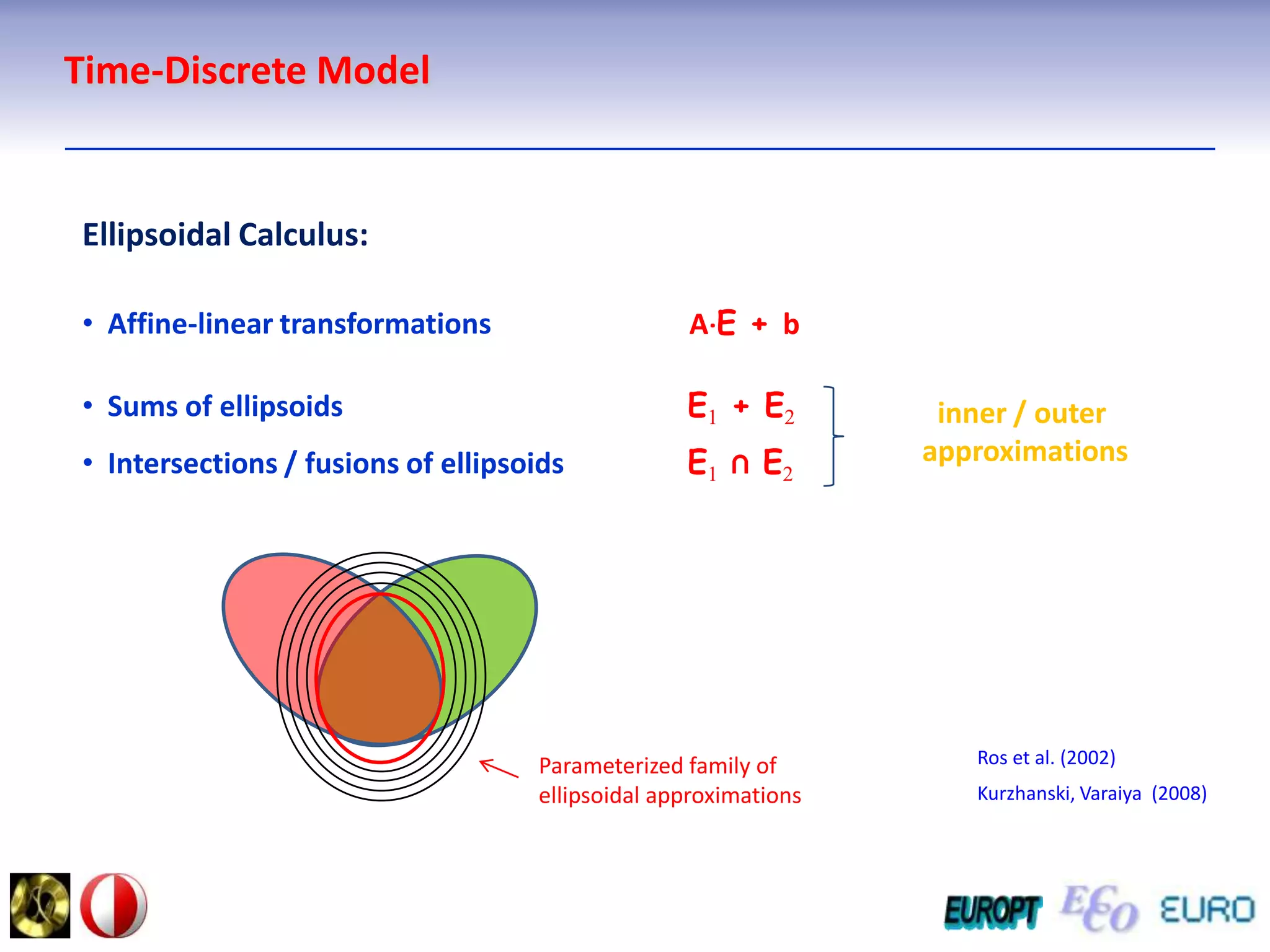
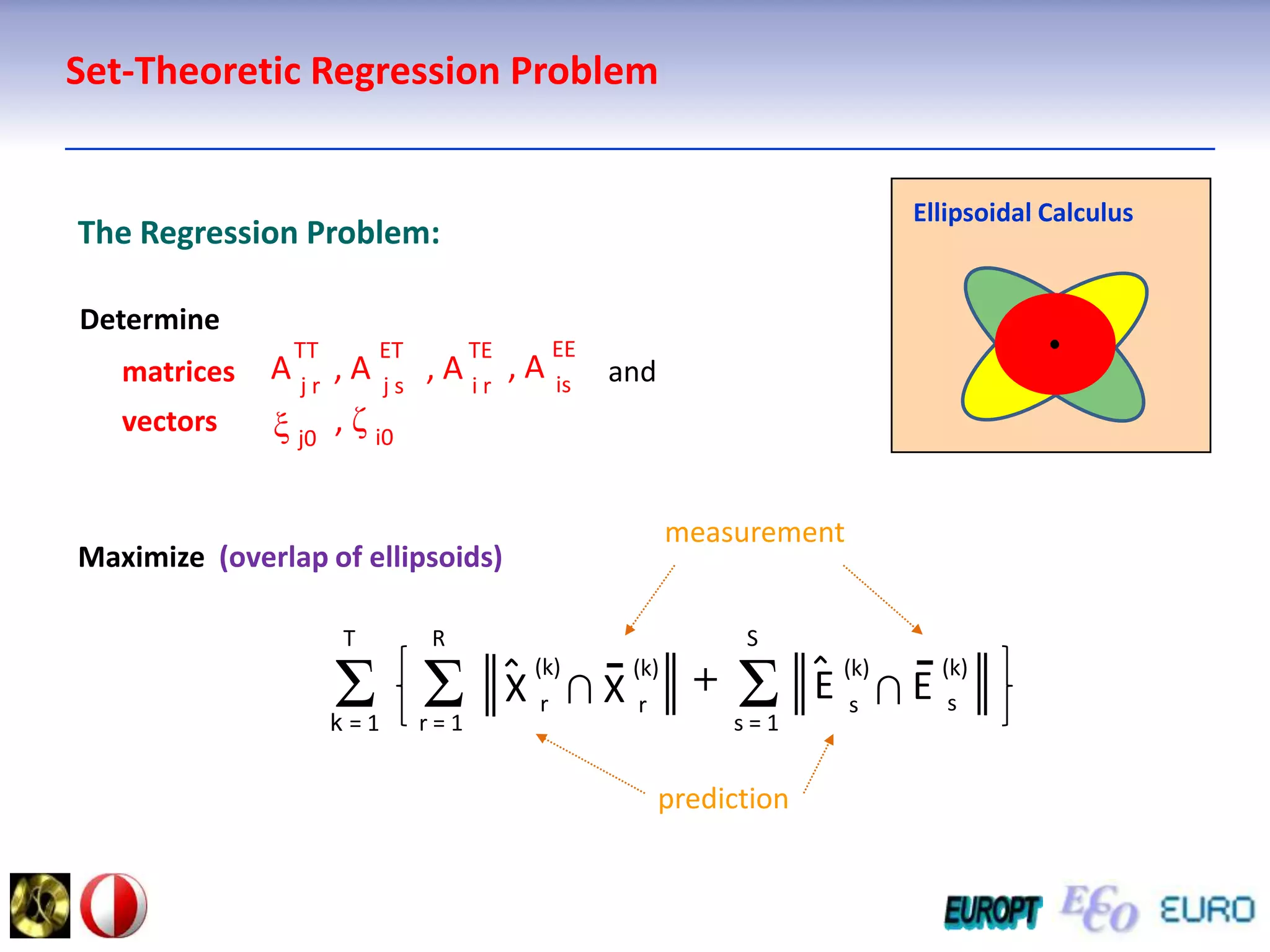
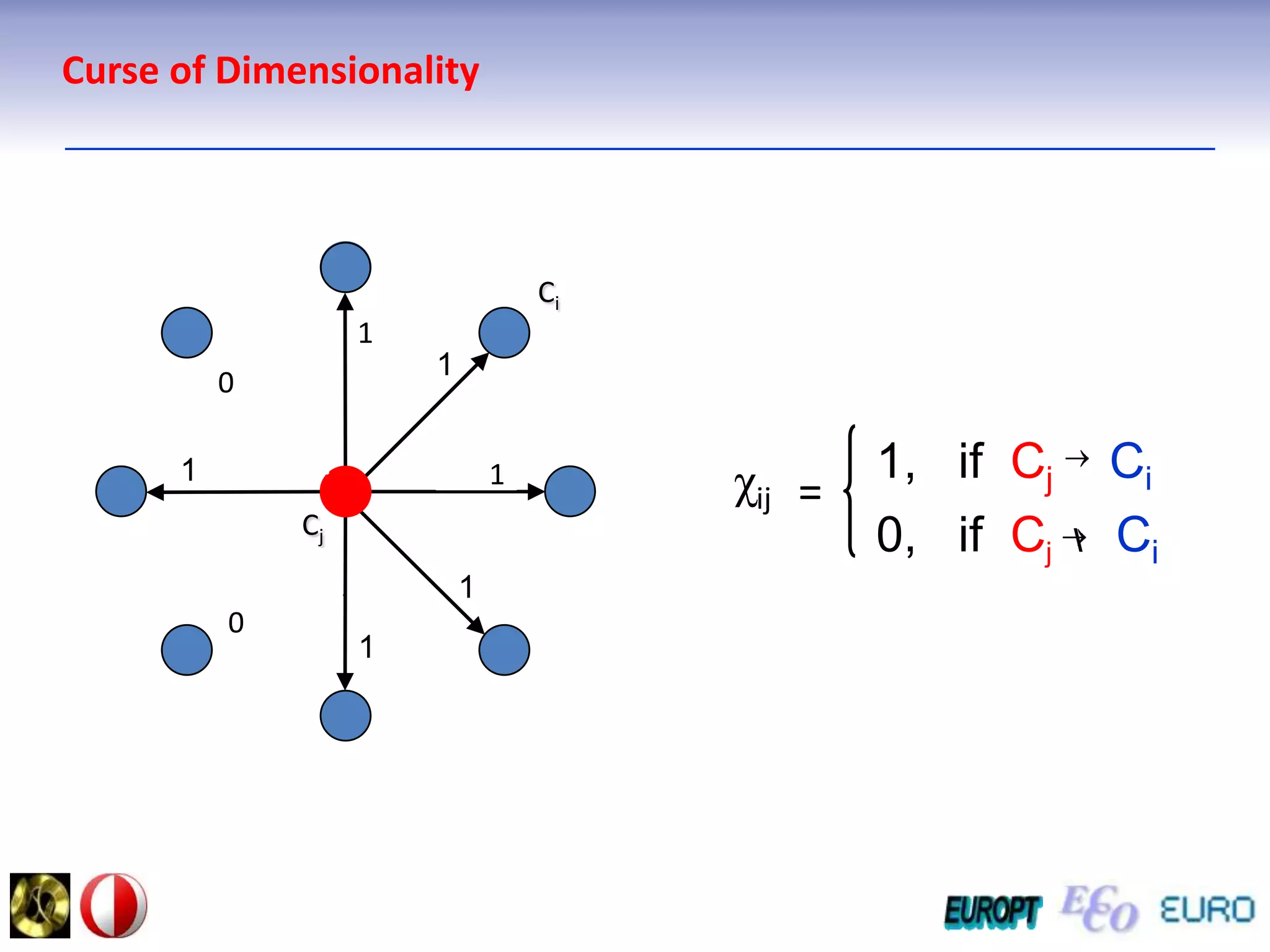
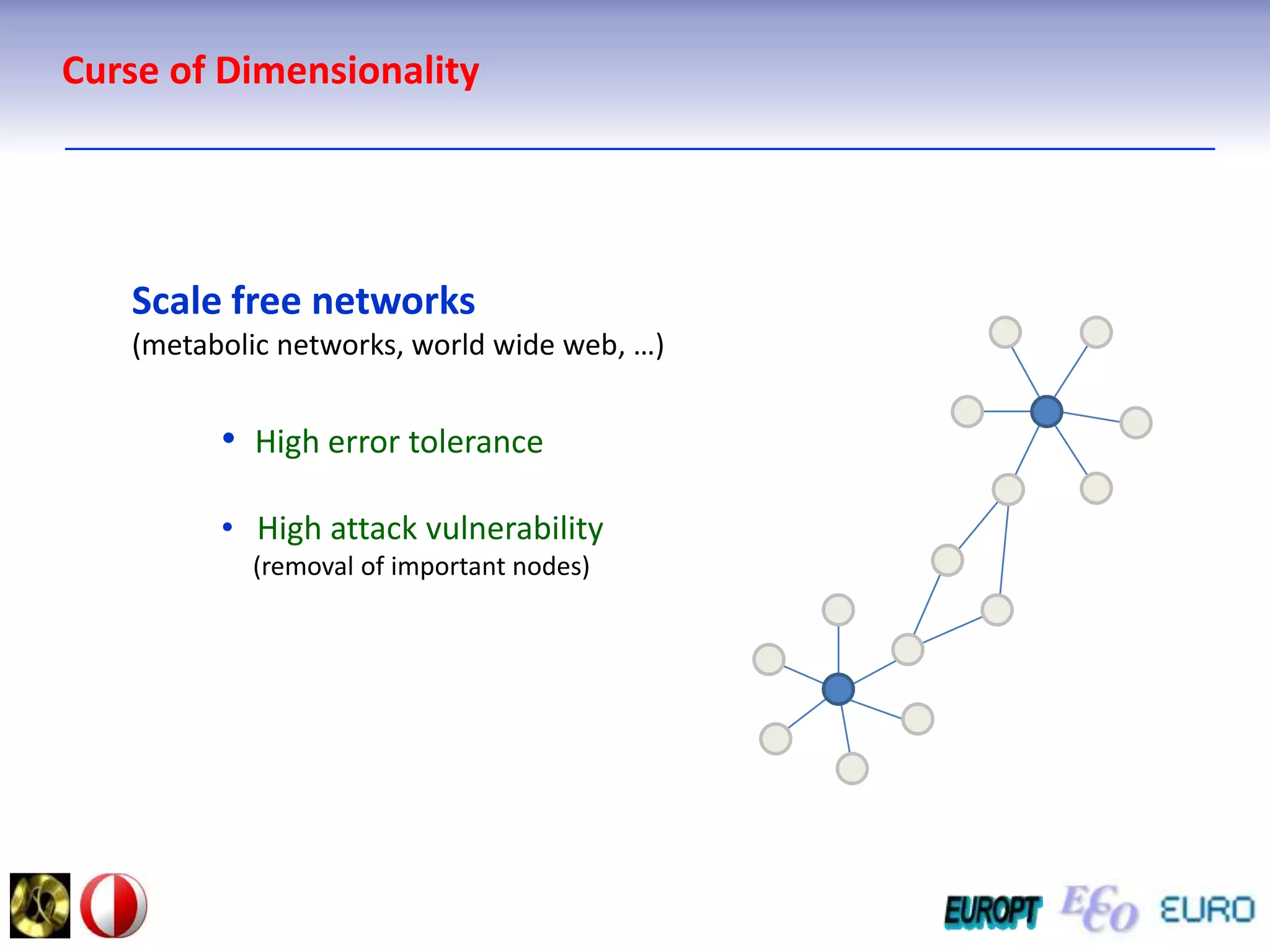
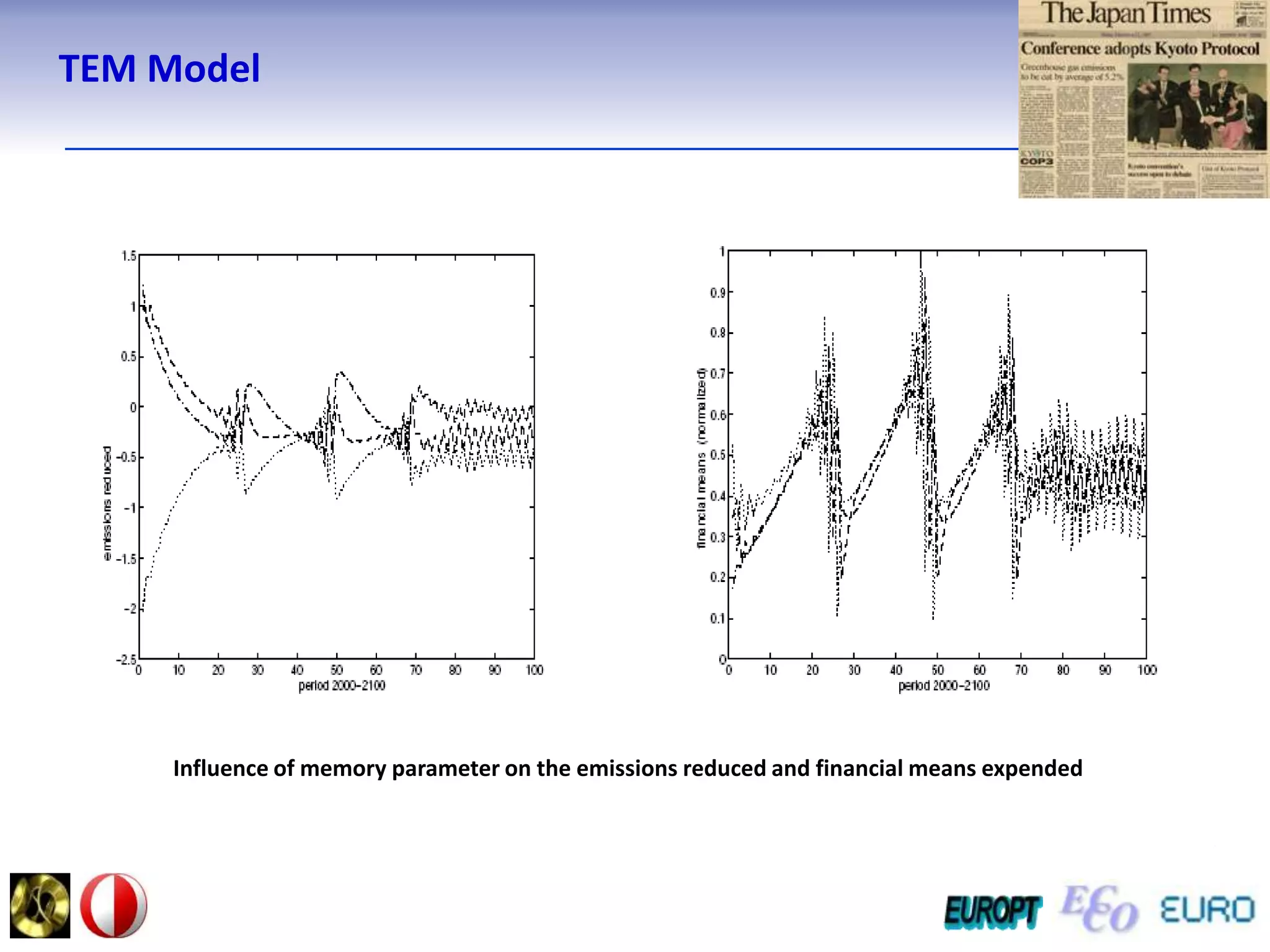
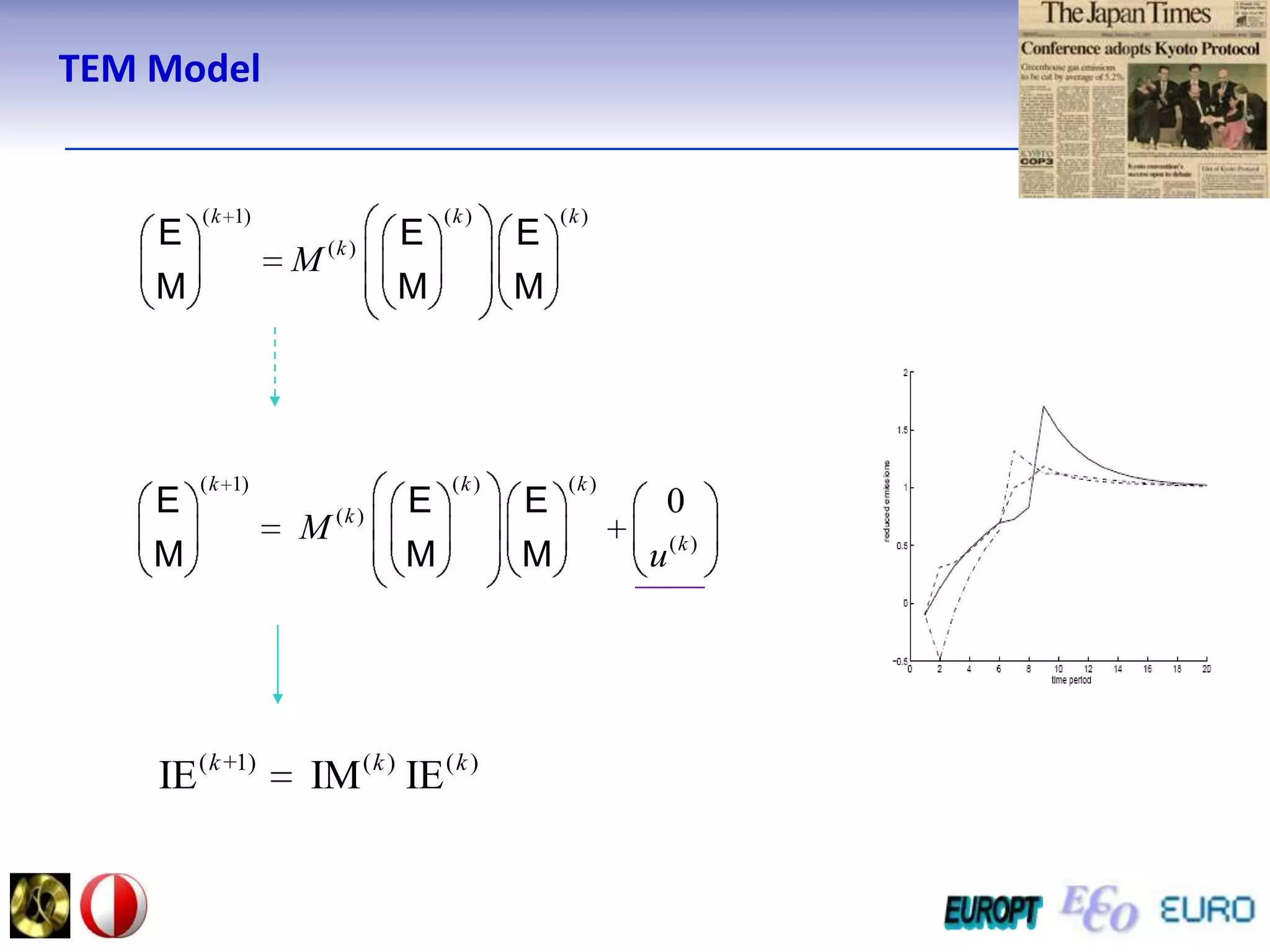
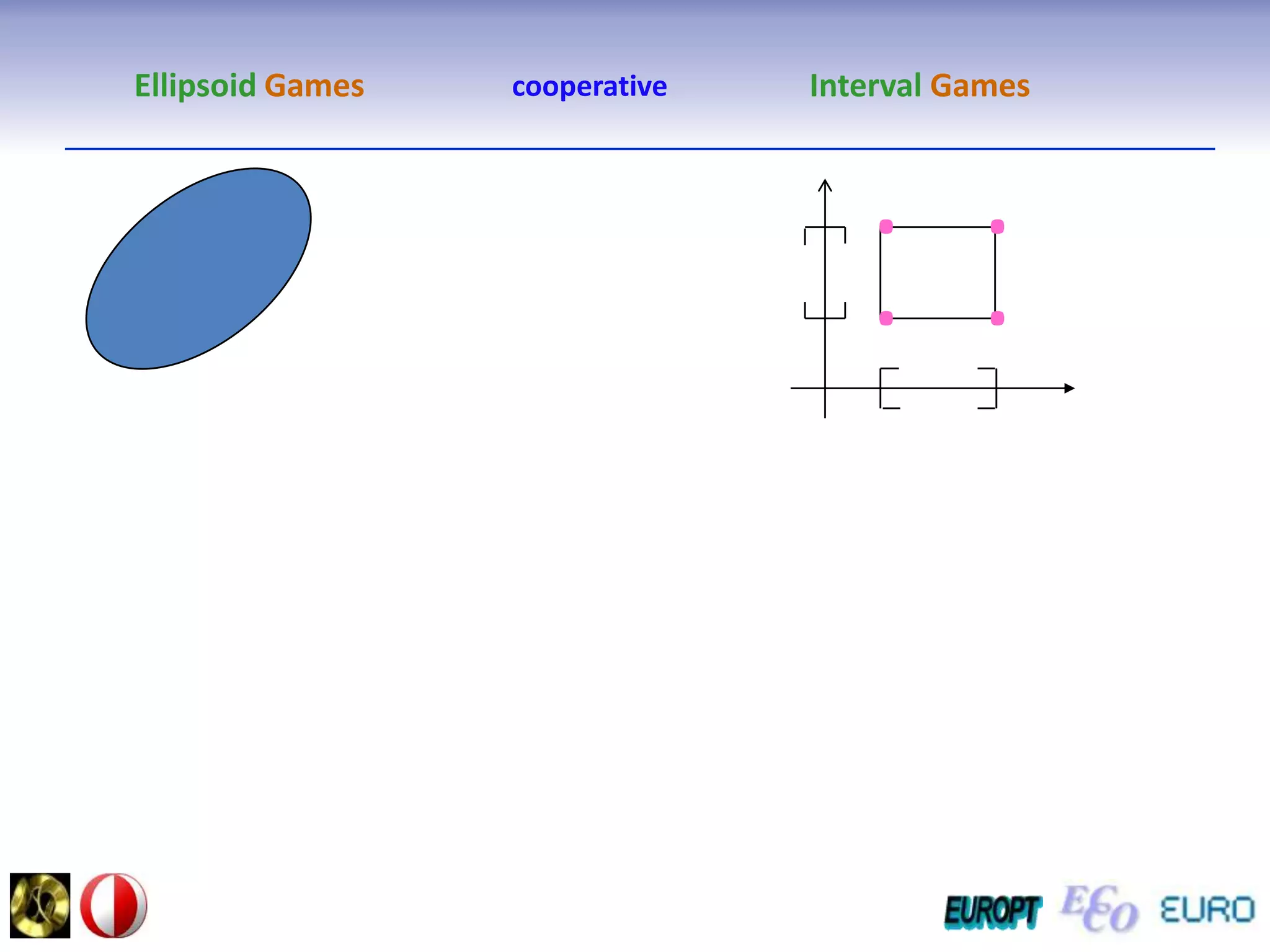
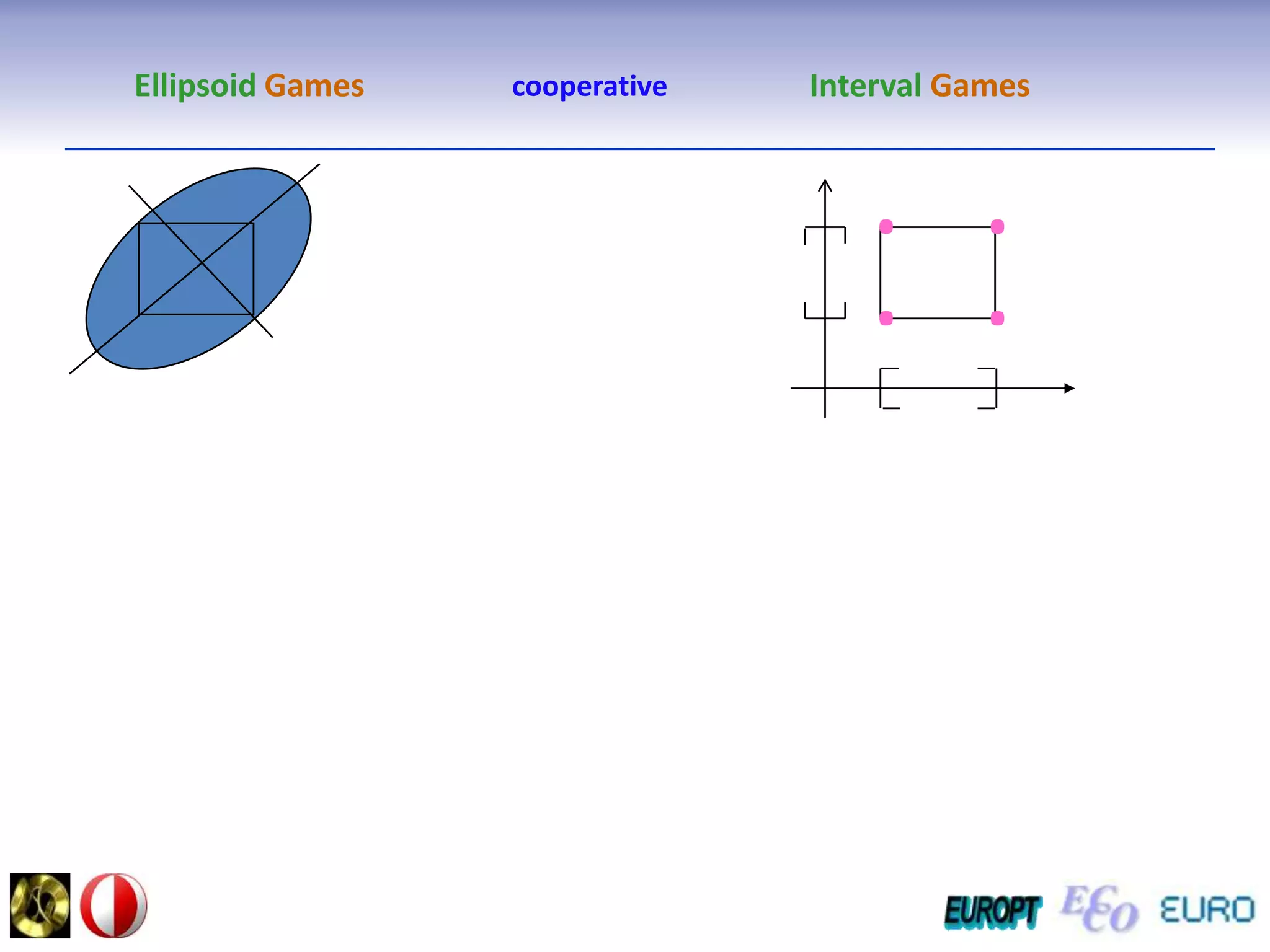
The document summarizes the outline and topics of the 6th International Summer School held in Kiev, Ukraine from August 8-20, 2011. The school focused on new insights and applications of eco-finance networks and collaborative games. Topics included bio-financial systems, genetic and gene-environment networks, time-continuous and time-discrete models, optimization problems, numerical examples and results, networks under uncertainty, the ellipsoidal model, and related aspects from finance. Modeling approaches included genetic, gene regulation, and gene-environment networks as well as optimization of parameters for stability and goodness of fit.