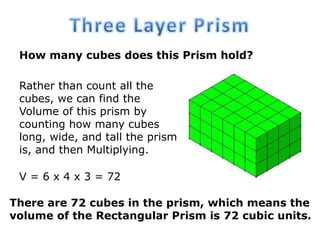
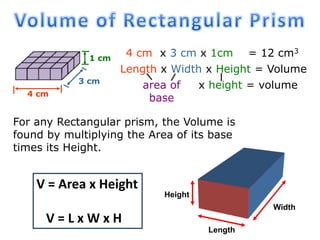
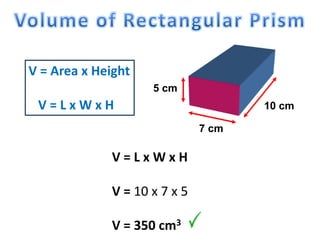
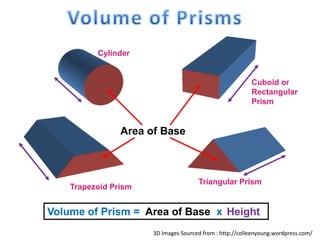
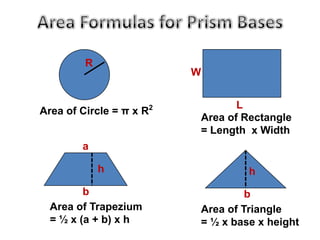
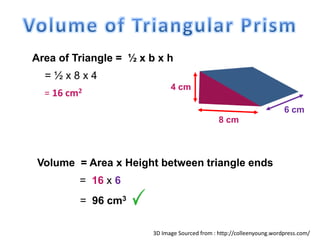
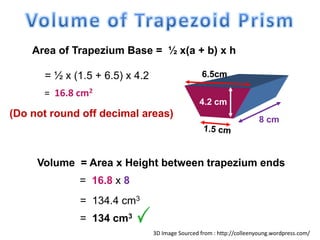
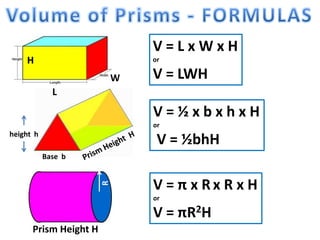
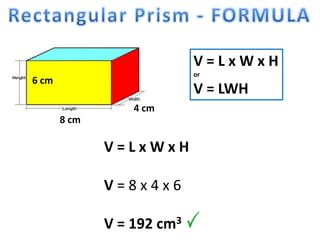
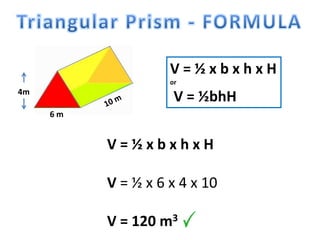
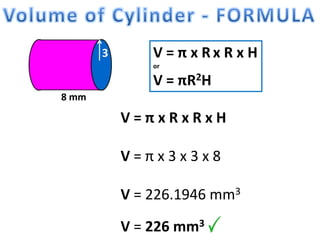
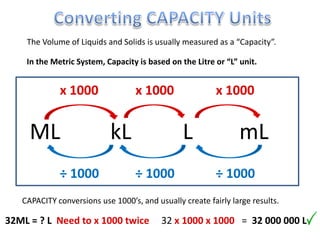
The document explains how to calculate the volume of various geometric shapes, particularly rectangular prisms, by multiplying their dimensions (length, width, height). It provides several volume examples and formulas for different shapes, including cylinders and prisms, emphasizing the importance of accurate calculations in practical applications like construction. Additionally, it mentions capacity conversions between millilitres, litres, and cubic meters for liquids and solids.

1. Image Source: http://www.noosaconcepts.com.au

2. Image Source: Google Images
Concreters, Air Conditioning Technicians,
Plumbers, Chemical Engineers, Road
Tanker Designers, Swimming Pool owners,
Medical Staff administering drugs, and
many other people need to know how to
accurately calculate Volumes.

3. How many 1cm3 cubes will fill the
Rectangular prism ?
The Volume of a 3D Shape is the number of cubes
needed to fill the inside of the shape.
Sixteen 1cm3 cubesImage Source: Google Images

4. How many cubes does this Prism hold?
Rather than count all the
cubes, we can find the
Volume of this prism by
counting how many cubes
long, wide and tall the prism
is, and then Multiplying.
V = 5 x 3 x 1 = 15
There are 15 cubes in the prism, which means the
volume of the Rectangular Prism is 15 cubic units.

5. How many cubes does this Prism hold?
Rather than count all the
cubes, we can find the
Volume of this prism by
counting how many cubes
long, wide, and tall the prism
is, and then Multiplying.
V = 5 x 3 x 2 = 30
There are 30 cubes in the prism, which means the
volume of the Rectangular Prism is 30 cubic units.

6. How many cubes does this Prism hold?
Rather than count all the
cubes, we can find the
Volume of this prism by
counting how many cubes
long, wide, and tall the prism
is, and then Multiplying.
V = 6 x 4 x 3 = 72
There are 72 cubes in the prism, which means the
volume of the Rectangular Prism is 72 cubic units.

7. 4 cm x 3 cm x 1cm = 12 cm3
Length x Width x Height = Volume
area of
base
x height = volume
For any Rectangular prism, the Volume is
found by multiplying the Area of its base
times its Height.
1 cm
4 cm
3 cm
Height
Length
Width
V = Area x Height
V = L x W x H

8. 5 cm
7 cm
10 cm
V = Area x Height
V = L x W x H
V = L x W x H
V = 10 x 7 x 5
V = 350 cm3

9. Cylinder
Cuboid or
Rectangular
Prism
Triangular Prism
Trapezoid Prism
Volume of Prism = Area of Base x Height
Area of Base
3D Images Sourced from : http://colleenyoung.wordpress.com/

10. Area of Circle = π x R2
R
Area of Rectangle
= Length x Width
W
L
b
h
Area of Triangle
= ½ x base x height
h
b
Area of Trapezium
= ½ x (a + b) x h
a

11. Area of Triangle = ½ x b x h
= ½ x 8 x 4
Volume = Area x Height between triangle ends
= 16 x 6
= 96 cm3
8 cm
6 cm
4 cm
4.9cm
= 16 cm2
3D Image Sourced from : http://colleenyoung.wordpress.com/

12. Area of Trapezium Base = ½ x(a + b) x h
= ½ x (1.5 + 6.5) x 4.2
8 cm
6.5cm
4.2 cm
= 16.8 cm2
(Do not round off decimal areas)
Volume = Area x Height between trapezium ends
= 16.8 x 8
= 134.4 cm3
= 134 cm3
3D Image Sourced from : http://colleenyoung.wordpress.com/

13. 5cm
3cm
Area of Circle Base = π x R2
= π x 32
= 28.2743…..cm2
Volume = Height x Area of Circle
= 5 x 28.2743….
= 141 cm3
Use full calculator ‘ANS’
for Area
= 141.3716….cm3
(Do not round off decimal areas)
3D Image Sourced from : http://colleenyoung.wordpress.com/

14. 1.6 m
For these types, we
have to be given the
Area of the Base.
We then use V = A x H
Area = 24 m2
Volume = Area of Irregular Base x Height
= 24 x 1.6
= 38.4 m3
= 38 m3
Image Source: www.cheappools.com.au

15. L
H
W
V = L x W x H
or
V = LWH
Base b
height h
V = ½ x b x h x H
or
V = ½bhH
Prism Height H
R
V = π x Rx R x H
or
V = πR2H

16. 8 cm
6 cm
4 cm
V = L x W x H
V = 8 x 4 x 6
V = 192 cm3
V = L x W x H
or
V = LWH

17. 6 m
4m
V = ½ x b x h x H
or
V = ½bhH
V = ½ x b x h x H
V = ½ x 6 x 4 x 10
V = 120 m3

18. 8 mm
3 V = π x R x R x H
or
V = πR2H
V = π x R x R x H
V = π x 3 x 3 x 8
V = 226.1946 mm3
V = 226 mm3

19. If we have a container filled with liquid or gas,
the Volume is specified in “Capacity” units.
Capacity units are Millilitres (mL), Litres (L),
Kilolitres (kL) and Megalitres (ML).
1 mL = 1 cm3 1 L = 1000 cm3
1 L = 1000 mL
1 ML = 1 000 000 L
1 m3 = 1000 L
1 L of Water weighs 1 kg

20. A cylindrical can of Coca Cola has a
volume of 375cm3, but is labeled as
375mL because it contains liquid.

21. The city of Melbourne’s main water storage (The
Thomson Dam) has a capacity of 1.07 million ML .
1 070 000 000 000 x 1 litre bottles of Coca Cola

22. In the Metric System, Capacity is based on the Litre or “L” unit.
ML kL L mL
x 1000 x 1000 x 1000
÷ 1000 ÷ 1000 ÷ 1000
32ML = ? L Need to x 1000 twice 32 x 1000 x 1000 = 32 000 000 L
CAPACITY conversions use 1000’s, and usually create fairly large results.
The Volume of Liquids and Solids is usually measured as a “Capacity”.

23. It can be seen in the above photo that we have a rectangular prism shaped Trench, containing a
cylindrical shaped Pipe. Cement is delivered in cubic meters, and the workers would need to have
calculated how much cement needed to be delivered for the job.
In this calculation they would need to have done Rectanglar Trench Volume minus the Volume of
the cylinder Pipe.
If they did not do this calculation carefully and correctly, then they would either have too much
cement, (which is expensive to dispose of), or not enough cement which could mean that they
would not be able to complete the job on time.
Image Source: http://alkispapadopoulos.com

24. http://passyworldofmathematics.com/
All slides are exclusive Copyright of Passy’s World of Mathematics
Visit our site for Free Mathematics PowerPoints