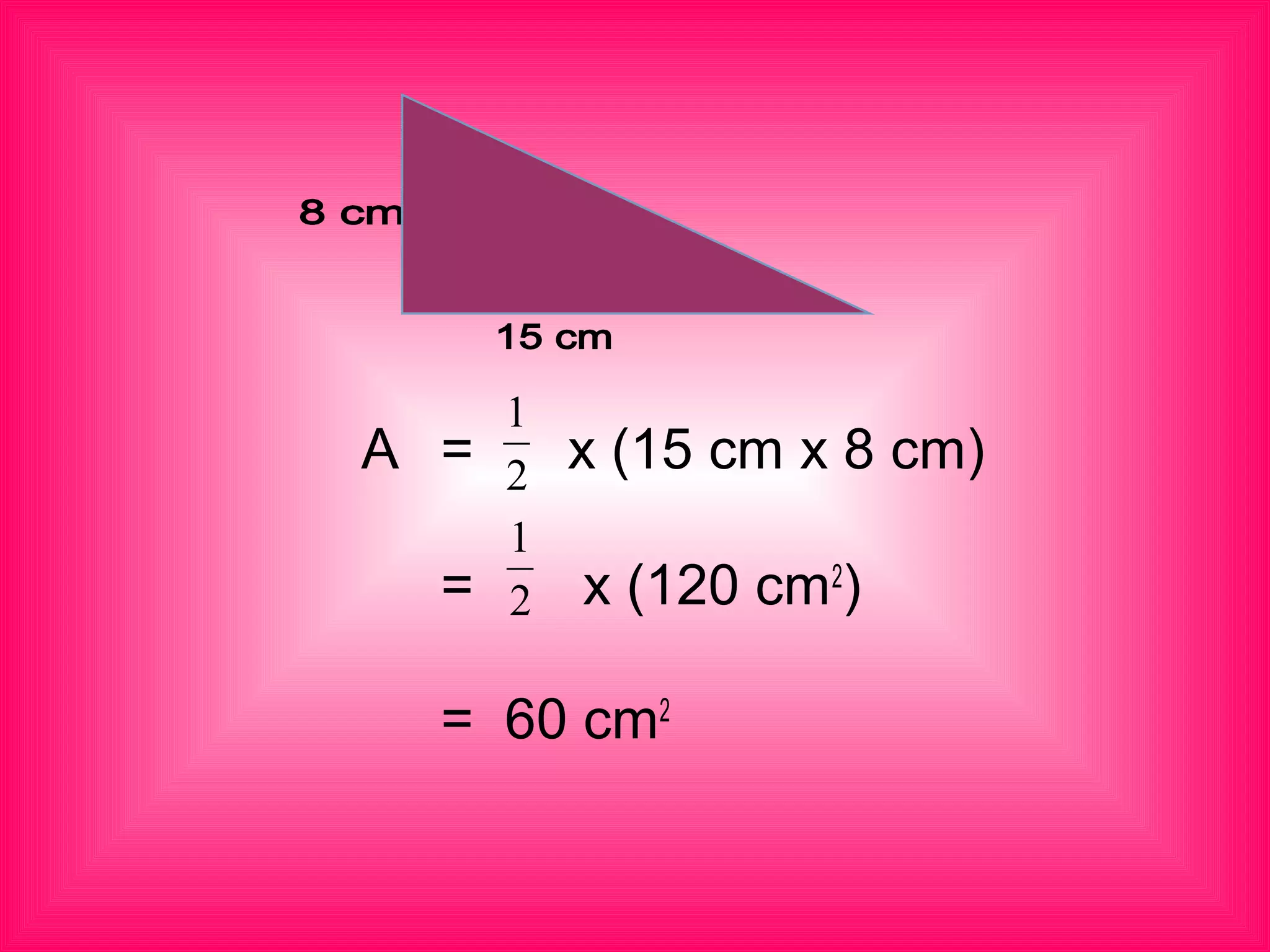
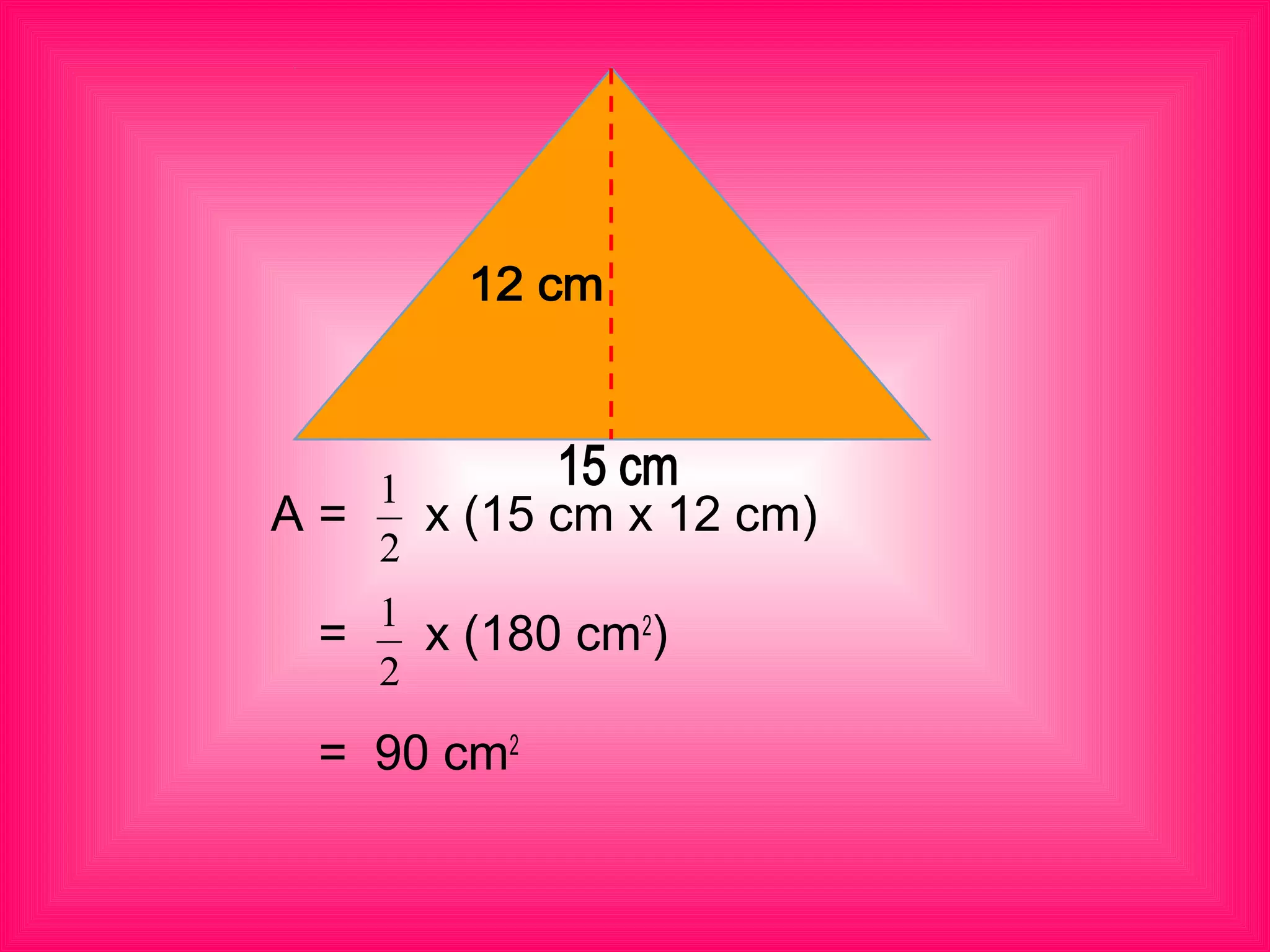
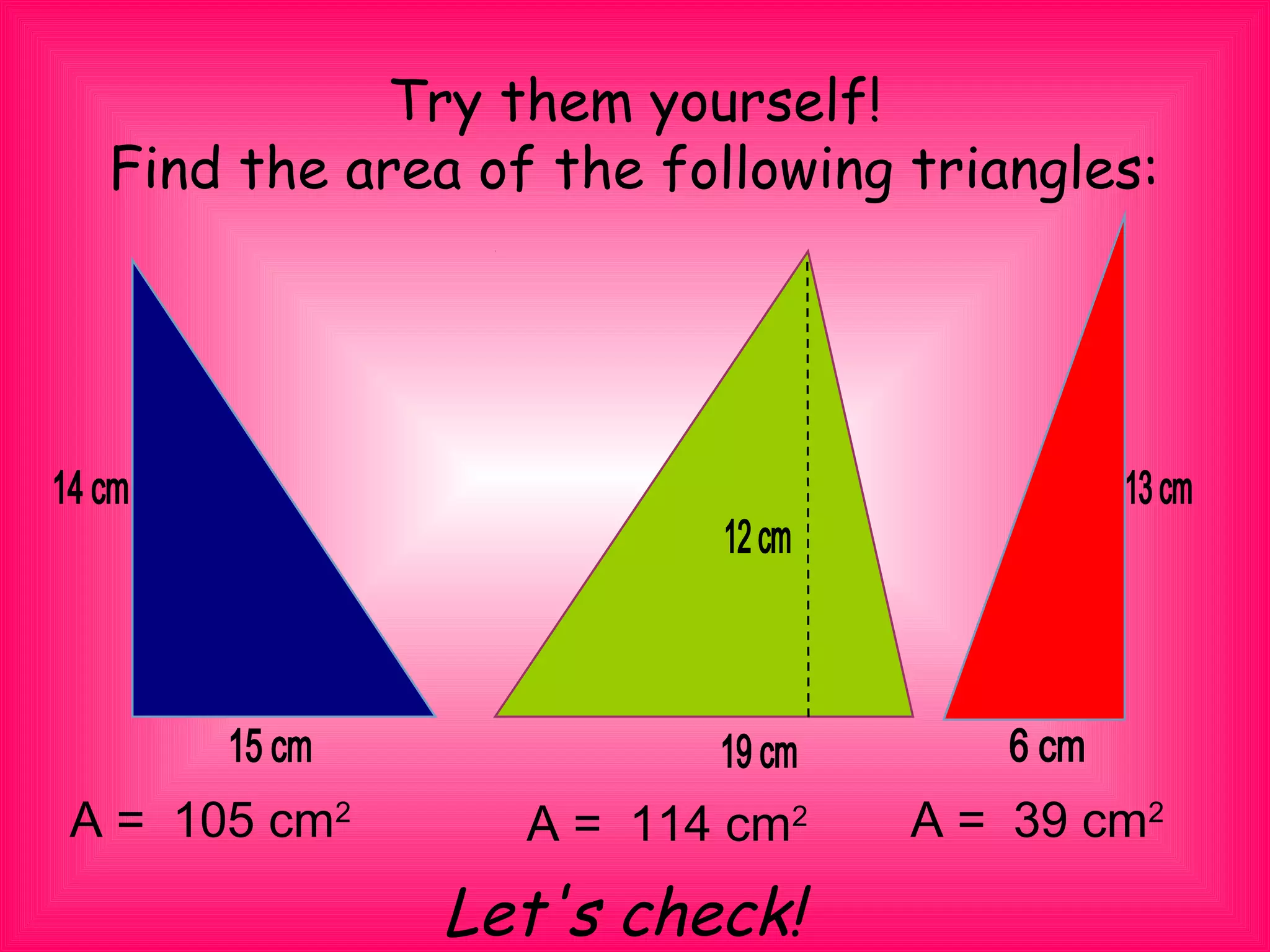
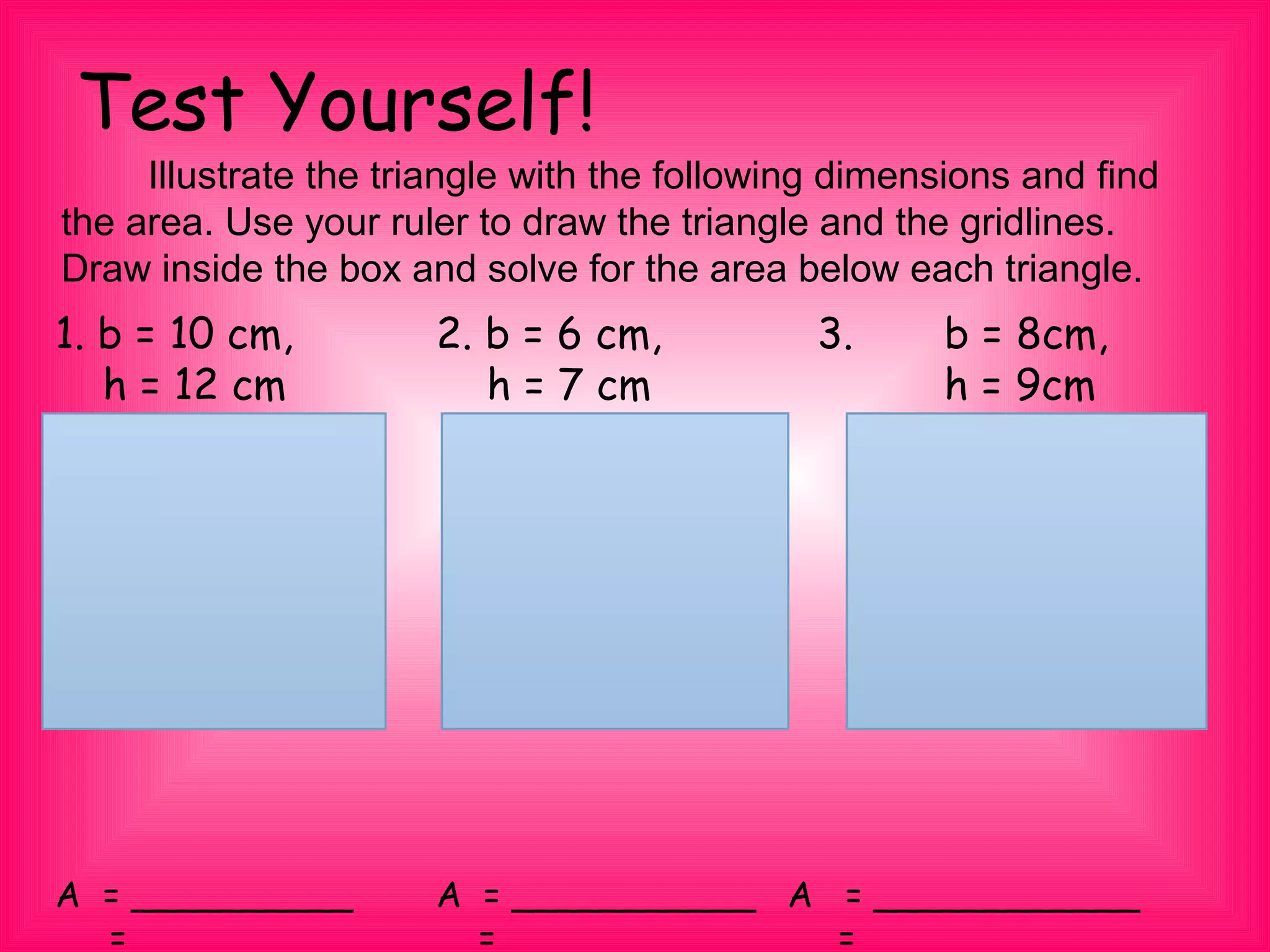
Joseph is planning to make a geometric collage of a volcano. He has a piece of navy blue cloth that is 17 cm long and 15 cm wide. He plans to cut it diagonally into two triangles. The document discusses deriving the formula for finding the area of a triangle. It states that the area of a triangle is equal to one-half base times height. It works through an example of finding the area of one of the triangles formed from Joseph's cloth, which is 127.5 cm^2. The document provides practice problems for readers to find the area of additional triangles.

1. Deriving the Formula forDeriving the Formula for
Finding the Area of aFinding the Area of a
TriangleTriangleby:
Aileen A. Garofil

2. How many triangles do you
see?

3. How about this, how many triangles
do you see?

4. Joseph is planning to make a
geometric collage of the scenic
Mayon Volcano. In his drawing canvas,
he plans to make a triangle using a
piece of navy blue cloth. He already
has a piece of cloth 17 cm long and
15cm wide so he decided to cut it
diagonally into 2. What is the area of
the resulting triangles?

6. • What kind of figures will be
formed by Joseph?
• Will the figures have the same
size, shape or area?
• How will you find the area of the
figures formed?

7. • I studied the situation and this is what I know ...
_____________________________________________
_____________________________________________
• This is what I don’t know ...
_____________________________________________
_____________________________________________
• This is what I need to know ...
_____________________________________________
_____________________________________________
• Here is how I solved the problem...

8.
Length = 17 cm, width = 15 cm
Recall: Area of a Quadrilateral = L x W or Base x Height or b x h
Area of a Triangle = 1/2 x (b x h)
= 1/2 x (17 cm x 15 cm)
= 1/2 x (255 cm2)
= 127.5 cm2

9. 2
1
A = x (15 cm x 8 cm)
= x (120 cm2
)
= 60 cm2
2
1

10. A = x (15 cm x 12 cm)
= x (180 cm2
)
= 90 cm2
2
1
2
1

11. A = x (17 cm x 15 cm)
= x (255 cm2
)
= 127.5 cm2
2
1
2
1

12. Try them yourself!
Find the area of the following triangles:
Let's check!
A = 105 cm2
A = 114 cm2 A = 39 cm2

13. • I studied the situation and this is what I know ...
_____________________________________________
_____________________________________________
• This is what I don’t know ...
_____________________________________________
_____________________________________________
• This is what I need to know ...
_____________________________________________
_____________________________________________
• Here is how I solved the problem... (How did you
derive the formula for the area of a triangle?)

14. 2
bxh
2
1
Formula:
Area of a triangle = =
x (bxh)
Where b is the base and
h is the height.
2
1 2
bxh

15. I am a triangle. My base is
_________ and my height is
__________. Therefore my area
is ________________.

16. Test Yourself!
1. b = 10 cm, 2. b = 6 cm, 3. b = 8cm,
h = 12 cm h = 7 cm h = 9cm
A = __________ A = ___________ A = ____________
= __________ = ___________ = ____________
Illustrate the triangle with the following dimensions and find
the area. Use your ruler to draw the triangle and the gridlines.
Draw inside the box and solve for the area below each triangle.

17. Assignment:
Cut out a triangle and paste itCut out a triangle and paste it
on your notebook. Measure theon your notebook. Measure the
base and the height using thebase and the height using the
ruler and find the area. Solveruler and find the area. Solve
below the triangle.below the triangle.

18. Dios Mabalos