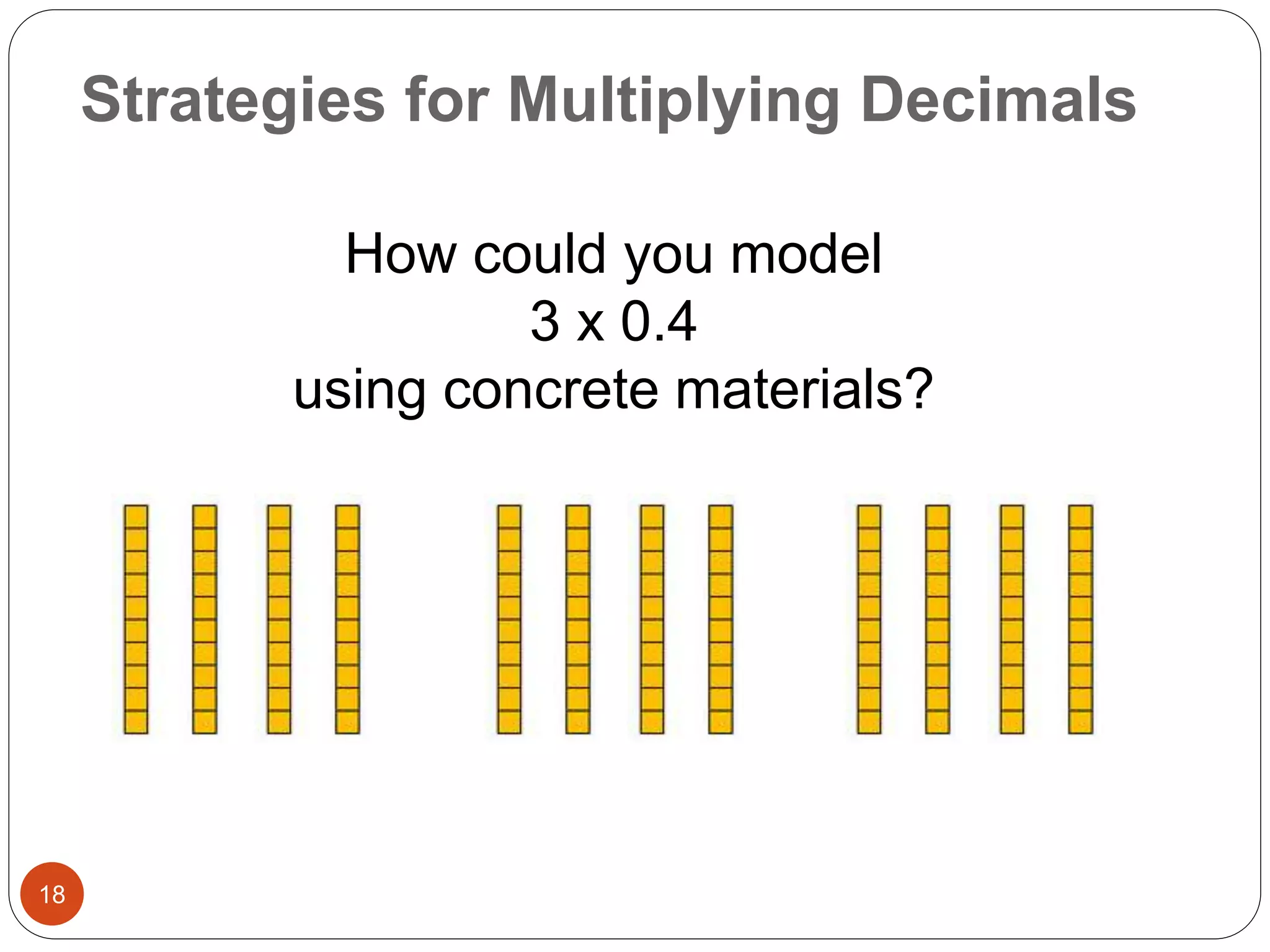
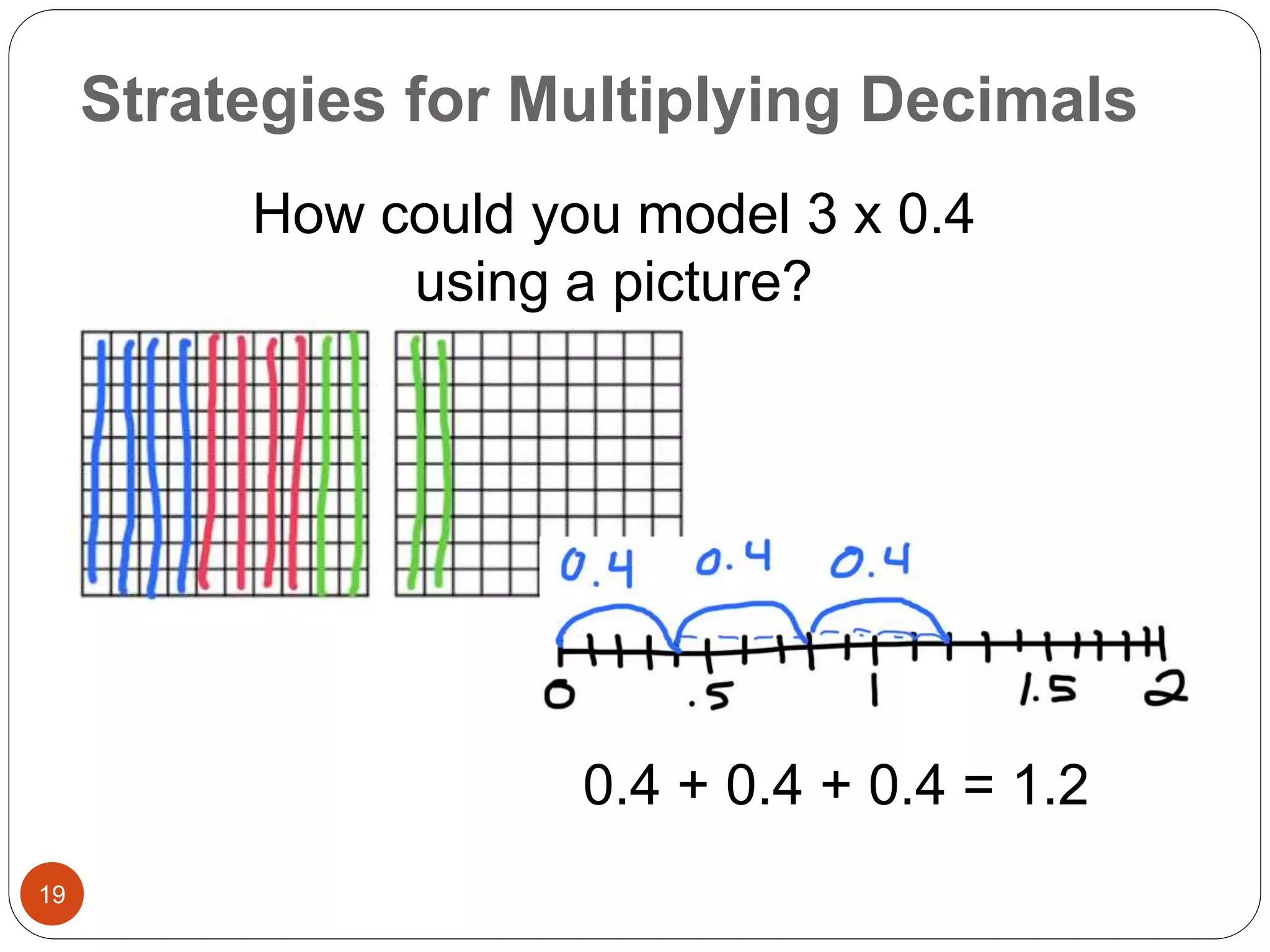
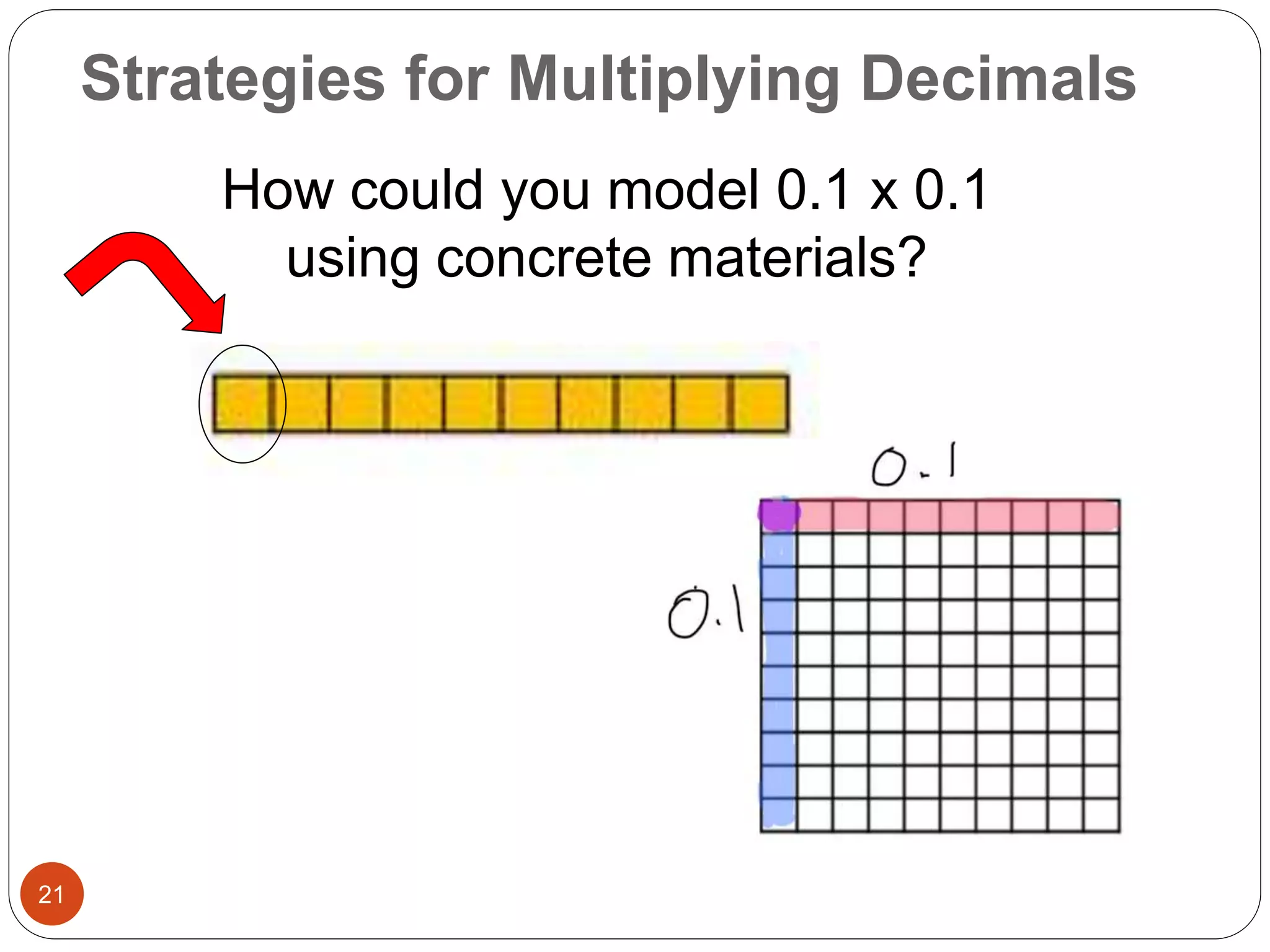
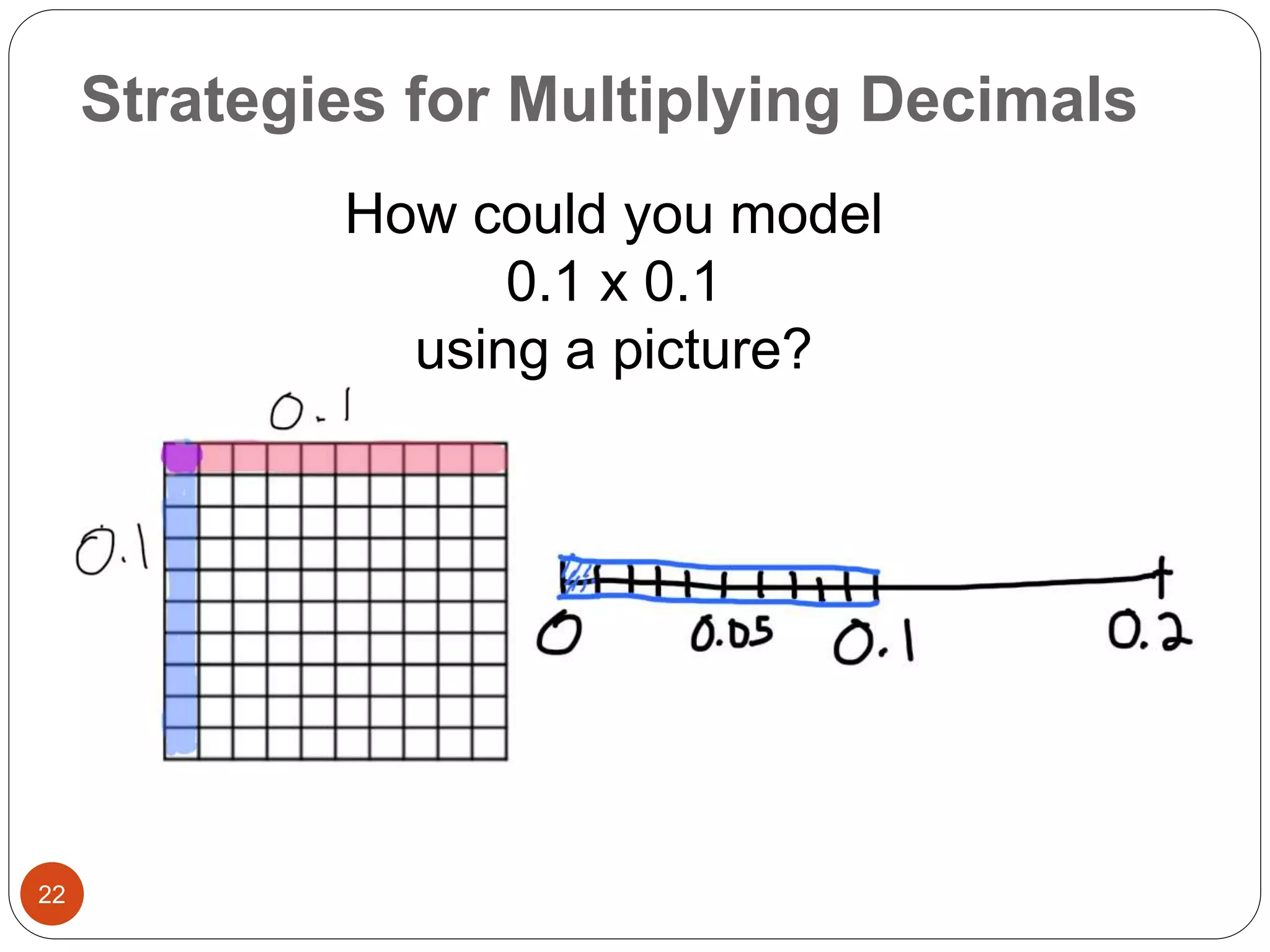
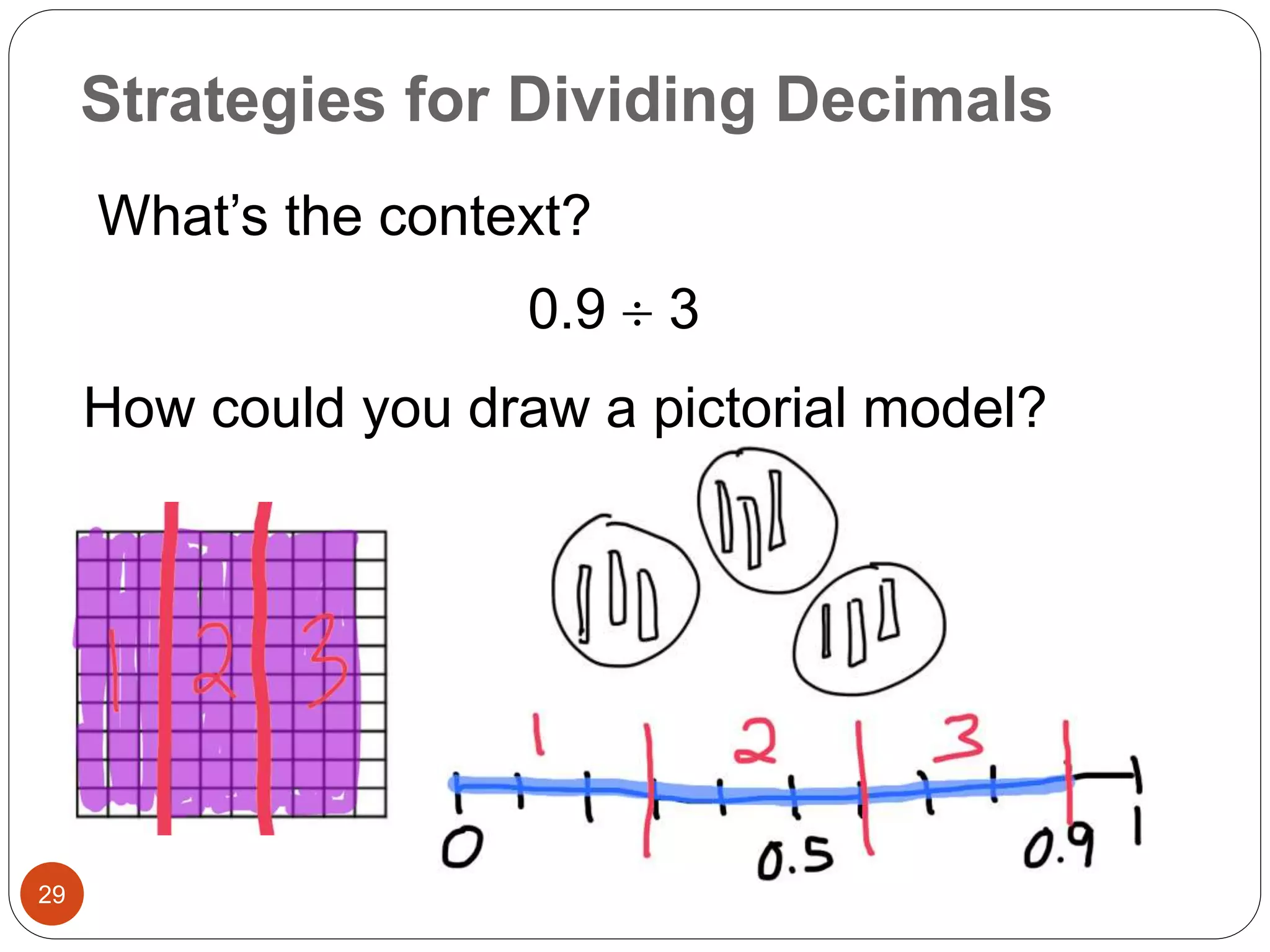
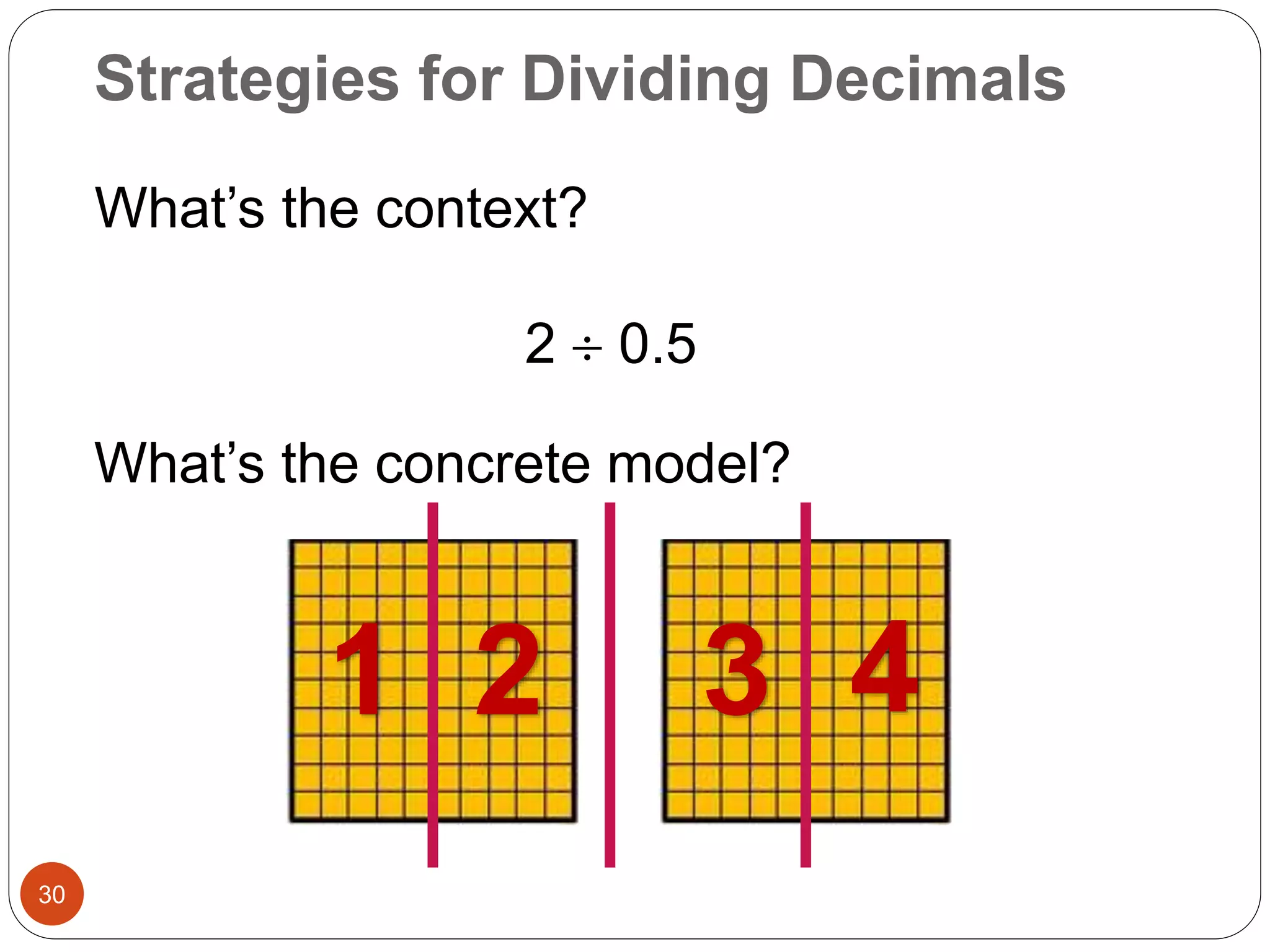
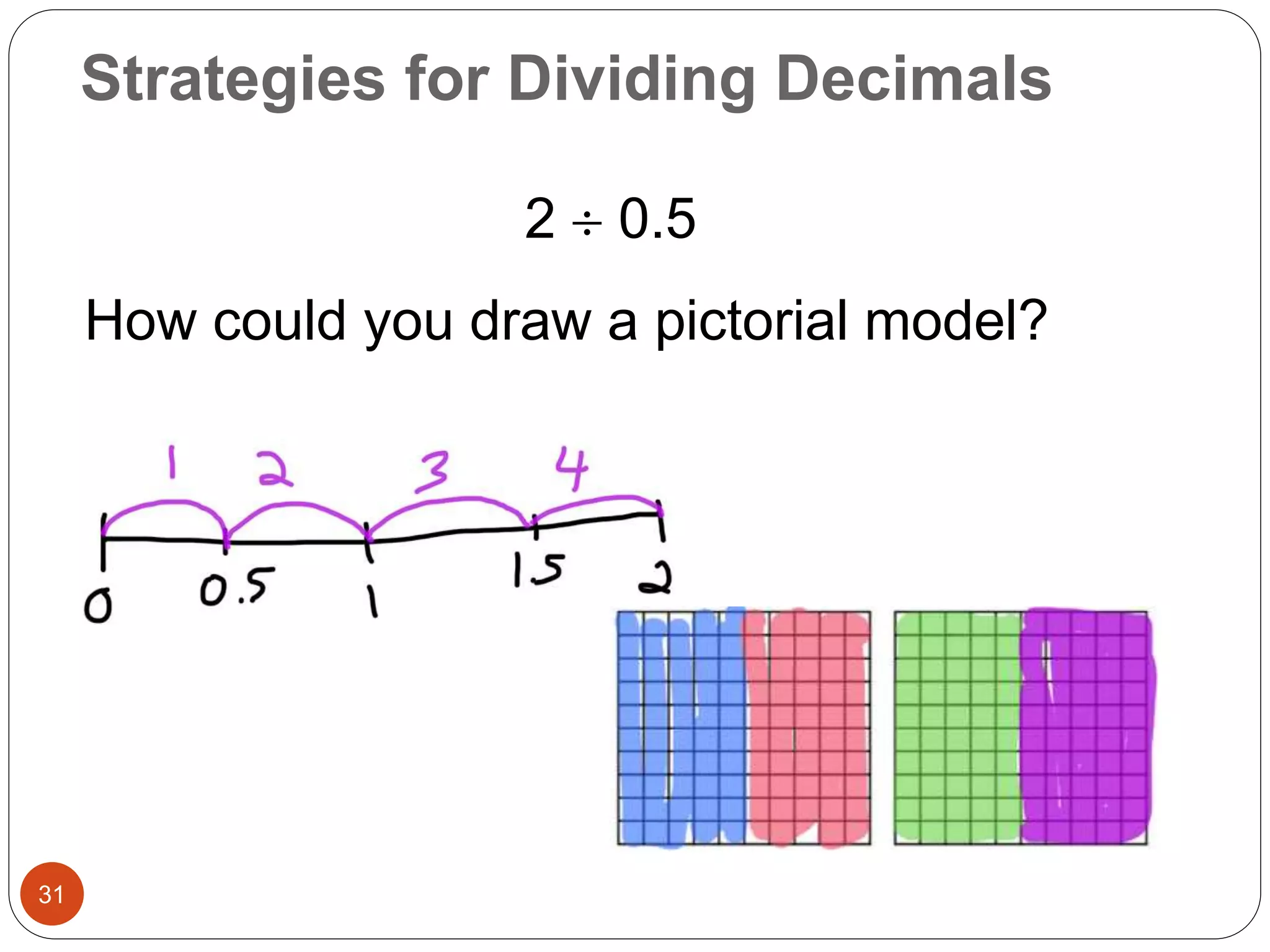
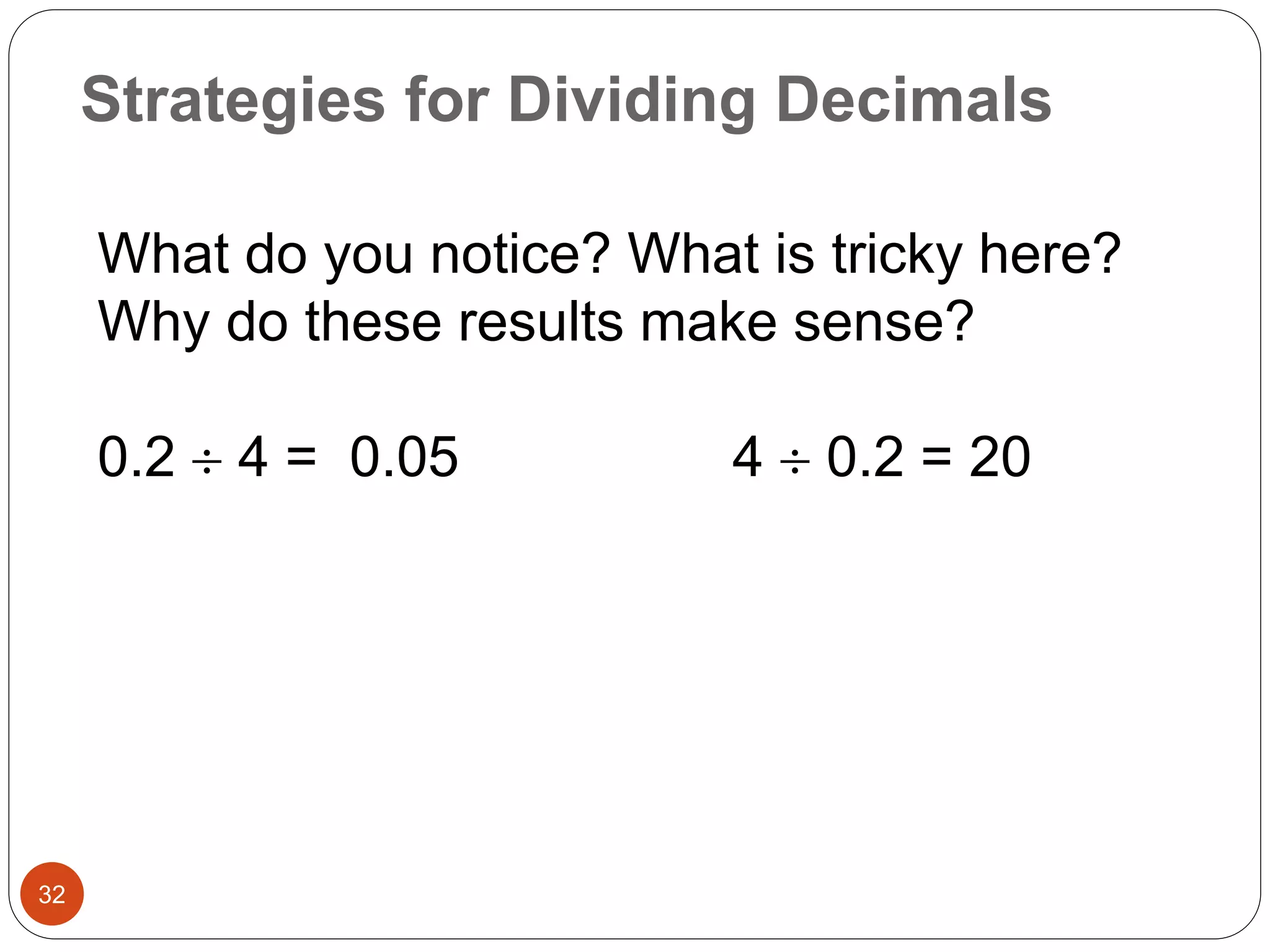
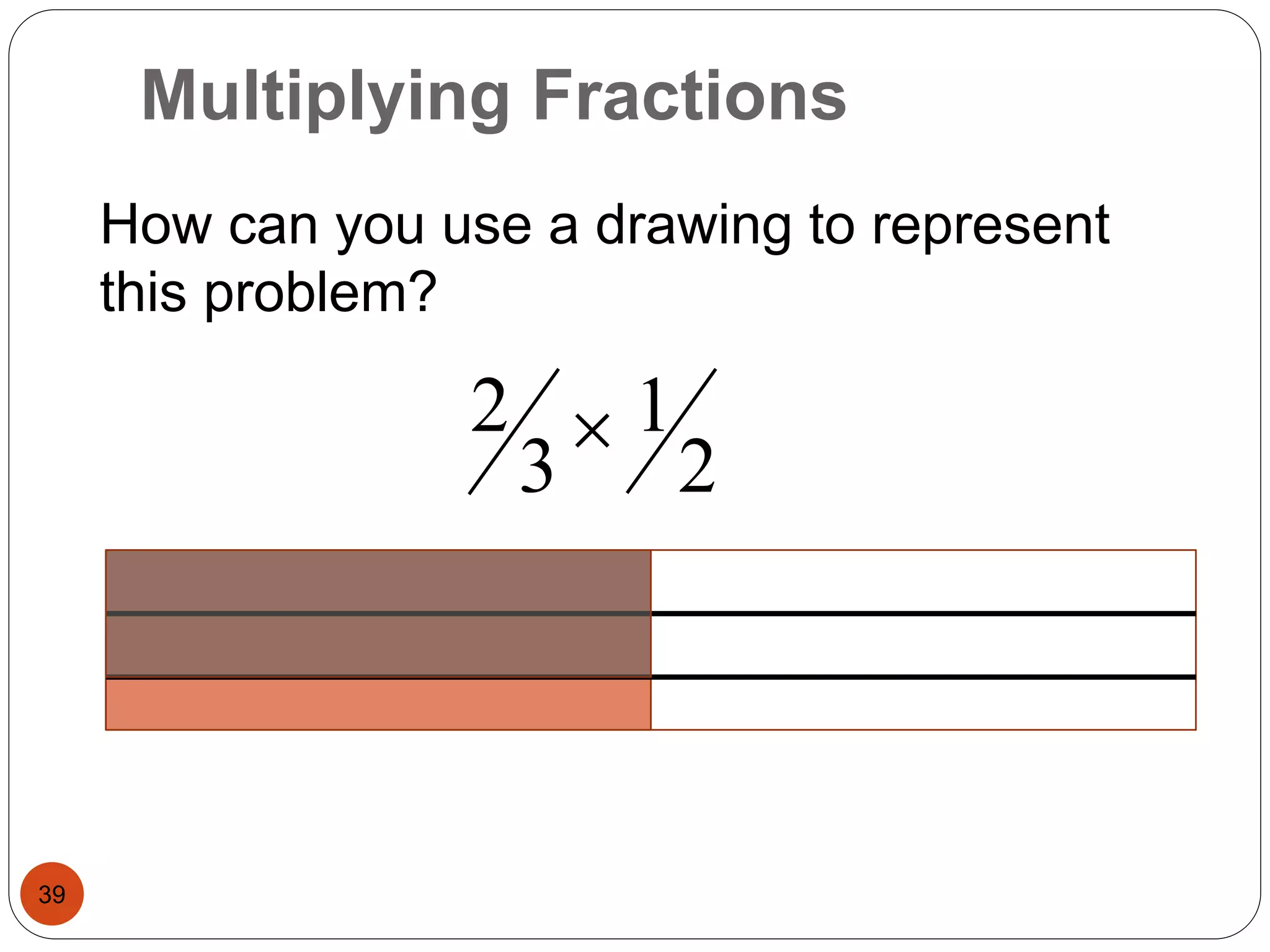
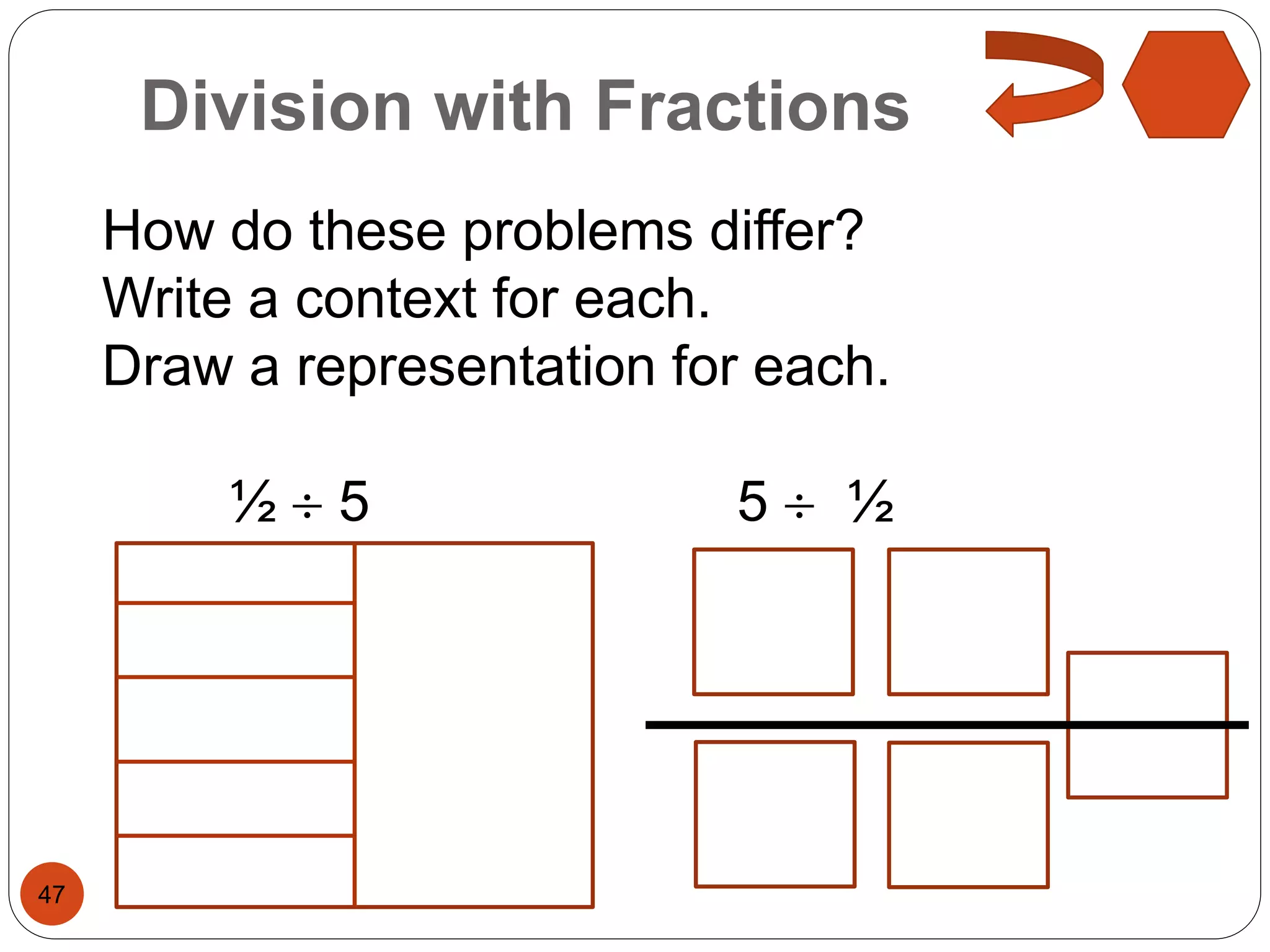
This document outlines instructional strategies for teaching multiplication and division of whole numbers, decimals, and fractions using the concrete-representational-abstract (CRA) approach. It provides examples of using physical objects, drawings, and standard algorithms to develop conceptual understanding at each stage. The CRA approach is demonstrated for topics like multiplying large whole numbers, dividing with decimals, and solving word problems involving fractions.