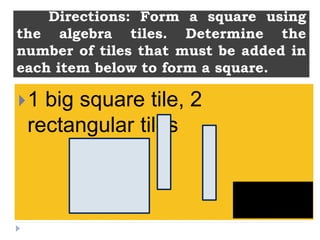
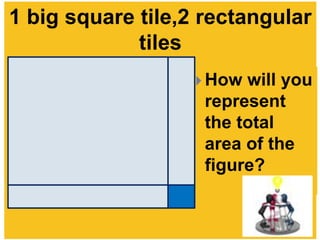
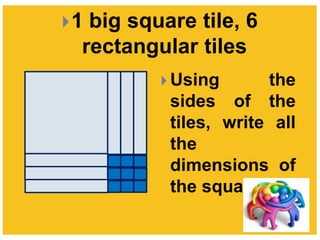
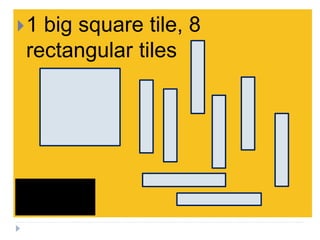
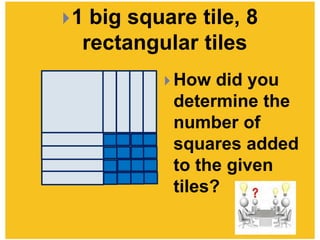
This document provides examples of completing the square to solve quadratic equations. It begins by showing how to factor a quadratic expression into a perfect square trinomial. It then demonstrates how to complete the square when the expression is not already a perfect square by adding or subtracting terms to make it a perfect square. The document provides step-by-step workings for several examples of completing the square to solve quadratic equations. It concludes by providing practice problems requiring students to find the solutions of quadratic equations by completing the square.

1. Demonstration Teaching
Basic Knowledge in Understanding Functions
Jayson G. Barsana
Demo Teacher

2. First
Term
𝑓𝑖𝑟𝑠𝑡 𝑡𝑒𝑟𝑚 Last
Ter
m
𝑙𝑎𝑠𝑡 𝑡𝑒𝑟𝑚 Factored
Form
𝒙 𝟐
+ 𝟒𝒙 + 𝟒
𝒙 𝟐 𝒙 𝟒 𝒙 + 𝟐 𝟐
𝟐

3. First
Term
𝑓𝑖𝑟𝑠𝑡 𝑡𝑒𝑟𝑚 Last
Ter
m
𝑙𝑎𝑠𝑡 𝑡𝑒𝑟𝑚 Factored
Form
𝒙 𝟐
+ 𝟐𝟎𝒙 + 𝟏𝟎𝟎
𝒙 𝟐 𝒙 𝟏𝟎𝟎 𝒙 + 𝟏𝟎 𝟐
1𝟎

4. First
Term
𝑓𝑖𝑟𝑠𝑡 𝑡𝑒𝑟𝑚 Last
Ter
m
𝑙𝑎𝑠𝑡 𝑡𝑒𝑟𝑚Factored
Form
𝟒𝒙 𝟐
+ 𝟏𝟐𝒙 + 𝟗
𝟒𝒙 𝟐 2𝒙 𝟗 𝟐𝒙 + 𝟑 𝟐
𝟑

5. First
Term
𝑓𝑖𝑟𝑠𝑡 𝑡𝑒𝑟𝑚 Last
Ter
m
𝑙𝑎𝑠𝑡 𝑡𝑒𝑟𝑚 Factored
Form
𝒙 𝟐
− 𝟏𝟒𝒙 + 𝟒𝟗
𝒙 𝟐 𝒙 𝟒𝟗 𝒙 − 𝟕 𝟐
𝟕

6. First
Term
𝑓𝑖𝑟𝑠𝑡 𝑡𝑒𝑟𝑚 Last
Ter
m
𝑙𝑎𝑠𝑡 𝑡𝑒𝑟𝑚 Factored
Form
𝒙 𝟐
+ 𝒙 +
𝟏
𝟒
𝒙 𝟐 𝒙 𝟏
𝟒
𝒙 +
𝟏
𝟐
𝟐𝟏
𝟐

7. Directions: Form a square using
the algebra tiles. Determine the
number of tiles that must be added in
each item below to form a square.
1 big square tile, 2
rectangular tiles

8. 1 big square tile,2 rectangular
tiles
 How will you
represent
the total
area of the
figure?

9. Directions: Form a square using
the algebra tiles. Determine the
number of tiles that must be added in
each item below to form a square.
1 big square tile, 6
rectangular tiles

10. 1 big square tile, 6
rectangular tiles
 Using the
sides of the
tiles, write all
the
dimensions of
the square.

11. 1 big square tile, 8
rectangular tiles

12. 1 big square tile, 8
rectangular tiles
 How did you
determine the
number of
squares added
to the given
tiles?

13. Directions: Form a square using
the algebra tiles. Determine the
number of tiles that must be added in
each item below to form a square.
4 big square tile, 4
rectangular tiles

14. 4 big square tile, 4
rectangular tiles
 How did you
determine the
number of
squares added
to the given
tiles?

15. Directions: Form a square using
the algebra tiles. Determine the
number of tiles that must be added in
each item below to form a square.
4 big square tile, 8
rectangular tiles

16. 4 big square tile, 8
rectangular tiles
 Did you find
pattern in
completing the
square? If yes,
what is this?

17. Directions: The
shaded region of the
diagram at the right
shows the portion of a
square-shaped car park
that is already
cemented. The area of
the cemented part is
600m2. Use the
diagram to answer the
following questions.
10m
10m

18. How would you represent the length of the
side of the park? How about the width of
the cemented portion?
10m
10m

19. What equation would represent the area of
the cemented part of the car?

20. Using the equation formulated, how are you
going to find the length of a side of the
park?

21. Completing the Square
 Another method of solving Quadratic
Equation
 𝒂𝒙 𝟐 + 𝐛𝐱 + 𝐜 = 𝟎
(𝒙 − 𝒉) 𝟐= 𝐤
 𝐤 ≠ 𝟎

22. C.Completing the square
Given the equation
x2+2x+1=4 , note that the
left-hand side is a perfect
square trinomial which can
be factored as (x+1)2. Thus
we can have…

23. 1212  xorx
Express the
PST in to
square of
binomial
Extracting the
square root
Solving
Linear
Equations
21 x
.31,  xorxThus
4)1( 2
x

24. Given the Quadratic equation
𝒙 𝟐
+ 𝟔𝒙 + 𝟗 = 𝟏
(𝒙 + 𝟑) 𝟐
= 𝟏
𝒙 + 𝟑 = ±𝟏
𝒙 = 𝟏 − 𝟑 𝒐𝒓 𝒙 = −𝟏 − 𝟑
𝑻𝒉𝒖𝒔, 𝒙 = −𝟐 𝒐𝒓 𝒙 = −𝟒

25. What if the left-hand side
of the quadratic equation
ax2+bx+c = 0 is not a perfect
square trinomial? Can we still
do the completing the
square? Let see!(Recall the
formula for squaring a
binomial)

26. 𝑥2
+10𝑥+ ? = 9+ ?
𝑥 + 10 = ±3
𝑥2
+ 10𝑥 + 25 = 9 + 25
(𝑥 + 10)2
= 9𝟏𝟎
𝟐
𝟐 = 𝟓 𝟐 = 𝟐𝟓
𝑥 = 3 − 10 𝑜𝑟 𝑥 = −3 − 10
𝑇ℎ𝑢𝑠, 𝑥 = −2 𝑜𝑟 𝑥 = −4
𝑥2
+ 10𝑥 = 9

27. 𝑥2
+3𝑥+ ? = 4+ ?
𝒙 +
𝟑
𝟐
= ±
𝟓
𝟐
(𝑥 +
3
2
)2 =
25
4
𝟑
𝟐
𝟐 =
𝟗
𝟒
=
𝟗
𝟒
𝑥 = 1 𝑜𝑟 𝑥 = −4
𝑇ℎ𝑢𝑠, 𝑥 = 1 𝑜𝑟 𝑥 = −4
3𝑥2
+ 9𝑥 = 12
4
9
4
4
9
32
 xx
Divide both sides of
equation by a then
simplify

28. Directions: Use each figure and
write the equation that represents
the area of the shaded region. Then
find the solutions to the equations
by completing the square.

29. Questions:
How did you come up
with the equation that
represents the shaded
region?
How did you find the
solution/s of each
equation
Do all solutions to
each equation
represent a particular
measure of each
figure? Explain your
answer.

30. Questions:
How did you come up
with the equation that
represents the shaded
region?
How did you find the
solution/s of each
equation
Do all solutions to each
equation represent a
particular measure of
each figure? Explain
your answer.

31. Directions: Find the
solutions/roots of each of the
following quadratic equations by
completing the square.
1. 𝒙 𝟐
+ 𝟏𝟐𝒙 + 𝟑𝟔 = 𝟐
2. 𝒙 𝟐
− 𝟐𝒙 = 𝟏
3. 𝒕 𝟐
− 𝟓𝒕 − 𝟔 = 𝟎
4. 𝟑𝒔 𝟐
+ 𝟖𝒙 + 𝟕 = 𝟑
5. 𝟐𝒓 𝟐
+ 𝟑𝒓 + 𝟔 = 𝟓

32. Assignment:
Directions: Find the solutions/roots
of each of the following quadratic
equations by completing the square.
1. 𝑥2
− 6𝑥 − 41 = 0
2. 4𝑥2
−32𝑥 = −28
3. 𝑤2
+6𝑤 − 11 = 0