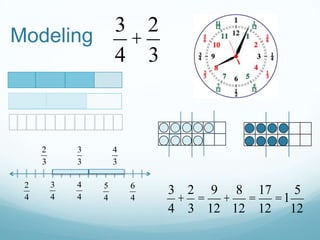
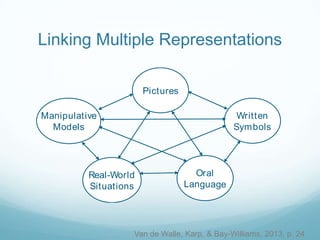
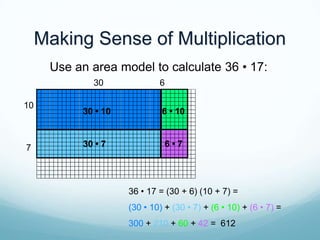
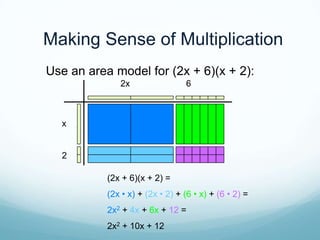
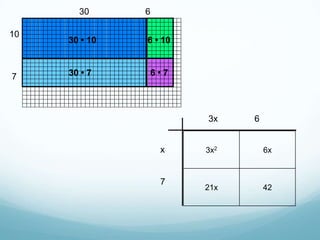
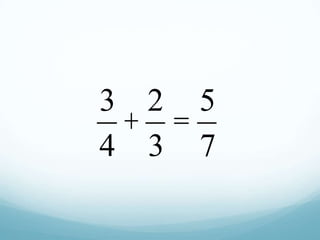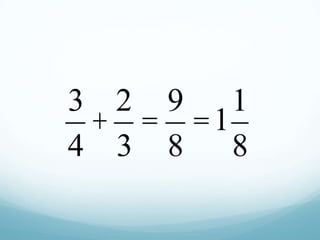The document discusses using mathematical modeling to develop mathematical habits of mind in students. It describes modeling as a means to support reasoning and sense-making. Research shows modeling helps students learn by linking multiple representations. The Common Core Standards for Mathematical Practice emphasize modeling with mathematics and using appropriate tools strategically. Modeling involves making sense of problems, not just getting answers. Linking representations, like using area models to understand multiplication, strengthens conceptual understanding. The goal is depth of learning, not just covering more topics.

1. How might you solve the following?
3 2
+
4 3

2. Practicing the
Mathematical Practices
Modeling to Develop
Mathematical Habits of Mind
Oregon Math Leaders Annual Conference
McMinnville, Oregon
Nicole Miller Rigelman
Portland State University
rigelman@pdx.edu

3. Overview
 Modeling as a means to support reasoning and sense
making
 What research says about modeling and how students
learn
 Example: using multiple representations to support sense
making
 Students experiences with models and tools
 Considering what else models can do…

4. What Mathematical Habits of Mind?
National Council of Teachers of
Mathematics Process Standards
• Problem Solving
• Reasoning and Proof
• Communication
• Connections
• Representations
- NCTM, 2000

5. What Mathematical Habits of Mind?
Strands of Mathematical Proficiency
1. Conceptual understanding—comprehension of
mathematical concepts, operations, and relations
2. Procedural fluency—skill in carrying out
procedures flexibly, accurately, efficiently, and
appropriately
3. Strategic competence—ability to formulate,
represent, and solve mathematical problems
4. Adaptive reasoning—capacity for logical
thought, reflection, explanation, and justification
5. Productive disposition—habitual inclination to
see mathematics as sensible, useful, and
worthwhile, coupled with a belief in diligence and
one’s own efficacy
- Kilpatrick, et al. 2001, p. 117

6. Standards for
Mathematical Practice
1. Make sense of problems and persevere in solving them.
2. Reason abstractly and quantitatively.
3. Construct viable arguments and critique the reasoning of others.
4. Model with mathematics.
5. Use appropriate tools strategically.
6. Attend to precision.
7. Look for and make use of structure.
8. Look for and express regularity in repeated reasoning.
- Common Core State Standards

7. Standards for
Mathematical Practice
1. Make sense of problems and persevere in solving them.
2. Reason abstractly and quantitatively.
3. Construct viable arguments and critique the reasoning of others.
4. Model with mathematics.
5. Use appropriate tools strategically.
6. Attend to precision.
7. Look for and make use of structure.
8. Look for and express regularity in repeated reasoning.
- Common Core State Standards

8. Why a focus on modeling?
Mathematically proficient students…
- model with mathematics
- use appropriate tools strategically

9. What answers might you expect?
3 2
+
4 3

10. 3 2 5
+ =
4 3 7

11. 3 2 9 1
+ = =1
4 3 8 8

12. 3 2
+
4 3

13. 3 2
+
4 3

14. Three Responses to a Problem
1. Answer getting
2. Making sense of the problem situation
3. Making sense of the mathematics you can learn from
working on the problem
- Daro, 2012

15. 3 2
+
4 3
Modeling
2
3
2
4
3
3
3
4
4
4
4
3
5
4
6
4
3 2 9 8 17
5
+ = + = =1
4 3 12 12 12 12

16. How would you use butterflies on this
problem?
1 1 1
+ +
2 3 4

17. Why a focus on modeling?
Mathematically proficient students…
- model with mathematics
- use appropriate tools strategically

18. Linking Multiple Representations
 The learner who can, for a particular mathematical
problem, move fluidly among different mathematical
representations has access to a perspective on the
mathematics in the problem that is greater than the
perspective any one representation can provide.
 Driscoll, 1999

19. Linking Multiple Representations
 Research has shown that children who have difficultly
translating a concept from one representation to
another are the same children who have difficulty
solving problems and understanding computations.
 Strengthening the ability to move between and among
these representations improves the growth of children’s
concepts.
 Lesh, Post, & Behr, 1987

20. Linking Multiple Representations
Pictures
Manipulative
Models
Written
Sym bols
Real-World
Situations
Oral
Language
Van de Walle, Karp, & Bay-Williams, 2013, p. 24

21. Mentally Compute
36 + 17

22. What if the problem were…
36 • 17

23. Multi-digit Multiplication
 Write a word problem that would be solved by
36 • 17.
 Create representations of 36 • 17 with
diagrams, base ten blocks, or cubes.

24. Link Sheet
Topic
______________________________________________
Mathematics Example
Situation/Context
Illustration/Model/Picture
My Explanation

25.  To find 36 + 17, I added the tens (30 + 10 = 40). I added
the ones (6 + 7 = 13) and added those together to get the
answer (40 + 13 = 53).
 Why isn’t 36 • 17 = (30 • 10) + (6 • 7)?

26.  To find 36 + 17, I added 4 to the 36 and 3 to the 17 to
make the problem easier (40 + 20 = 60). Then I
subtracted the extra 4 and the extra 3 to get the final
answer (60 – 4 – 3 = 53).
 Why not solve 36 • 17 the same way? 40 • 20 = 800 and
then subtract the extra 4 and the extra 3 to get 800 – 4 –
3 = 793?

27. Making Sense of Multiplication
Use an area model to calculate 36 • 17:
30
10
7
6
30 • 10
6 • 10
30 • 7
6•7
36 • 17 = (30 + 6) (10 + 7) =
(30 • 10) + (30 • 7) + (6 • 10) + (6 • 7) =
300 + 210 + 60 + 42 = 612

28. Making Sense of Multiplication
Use an area model for (2x + 6)(x + 2):
2x
6
x
2
4x
(2x + 6)(x + 2) =
(2x • x) + (2x • 2) + (6 • x) + (6 • 2) =
2x2 + 4x + 6x + 12 =
2x2 + 10x + 12

29. Making Sense of Multiplication
Use an area model for (3x + 6)(x + 7):
3x
x
7
3x2
6
6x
(3x + 6)(x + 7) =
21x
42
(3x • x) + (3x • 7) + (6 • x) + (6 • 7) =
3x2 + 21x + 6x + 42 =
3x2 + 27x + 42

30. 30
10
7
6
30 • 10
6 • 10
30 • 7
6•7
3x
x
7
6
3x2
6x
21x
42

31. 36 • 17 = (30 + 6) (10 + 7) =
(30 • 10) + (30 • 7) + (6 • 10) + (6 • 7) =
300 + 210 + 60 + 42 =
612
(3x + 6)(x + 7) =
(3x • x) + (3x • 7) + (6 • x) + (6 • 7) =
3x2 + 21x + 6x + 42 =
3x2 + 27x + 42

32.  ―We want our standards to be higher which
means deeper not wider. So we shouldn’t be
worried about getting the width of the
standards, that’s what cover means; we should
be worried about depth, that’s what learn
means.‖
- Daro, 2012