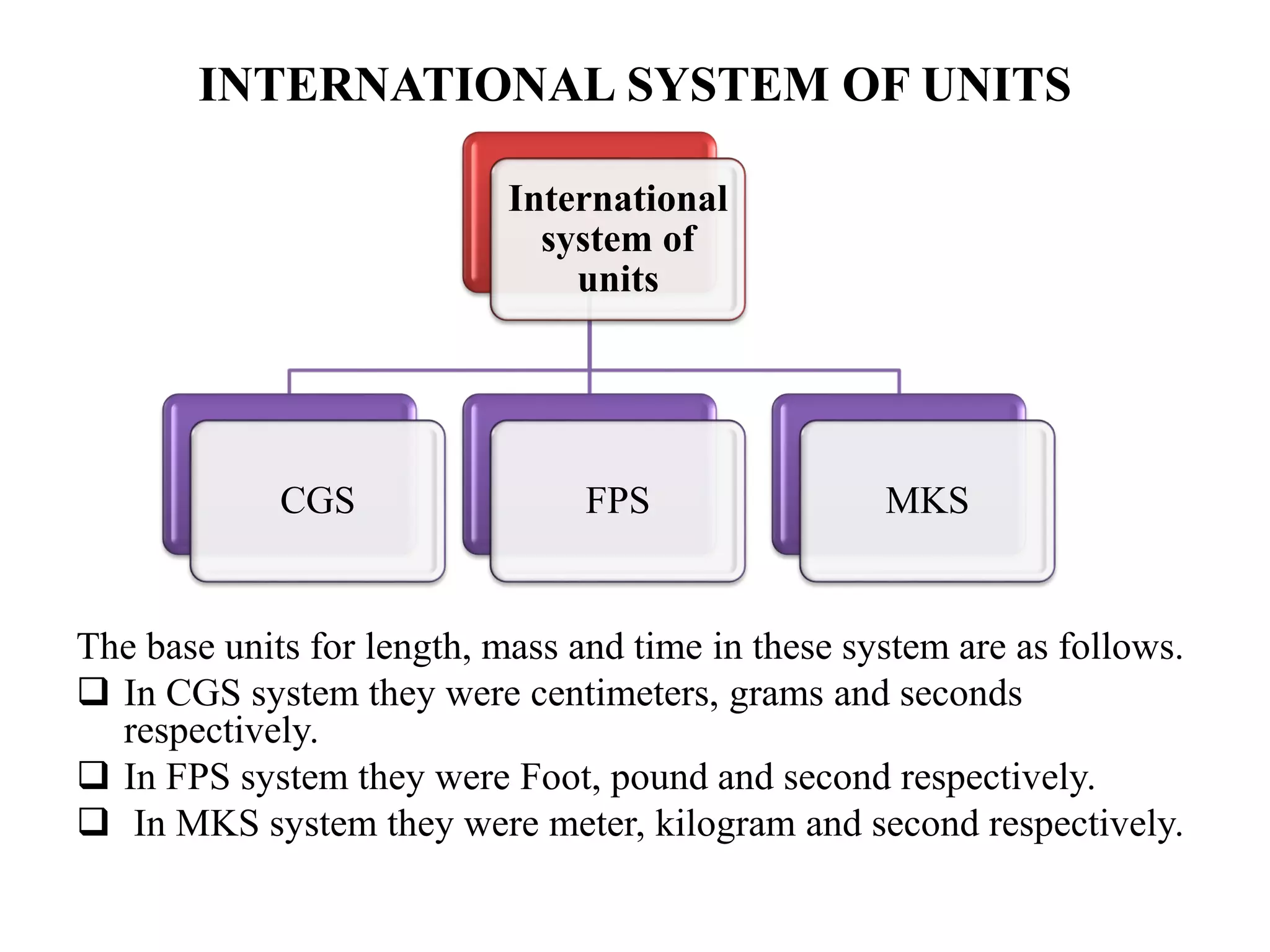
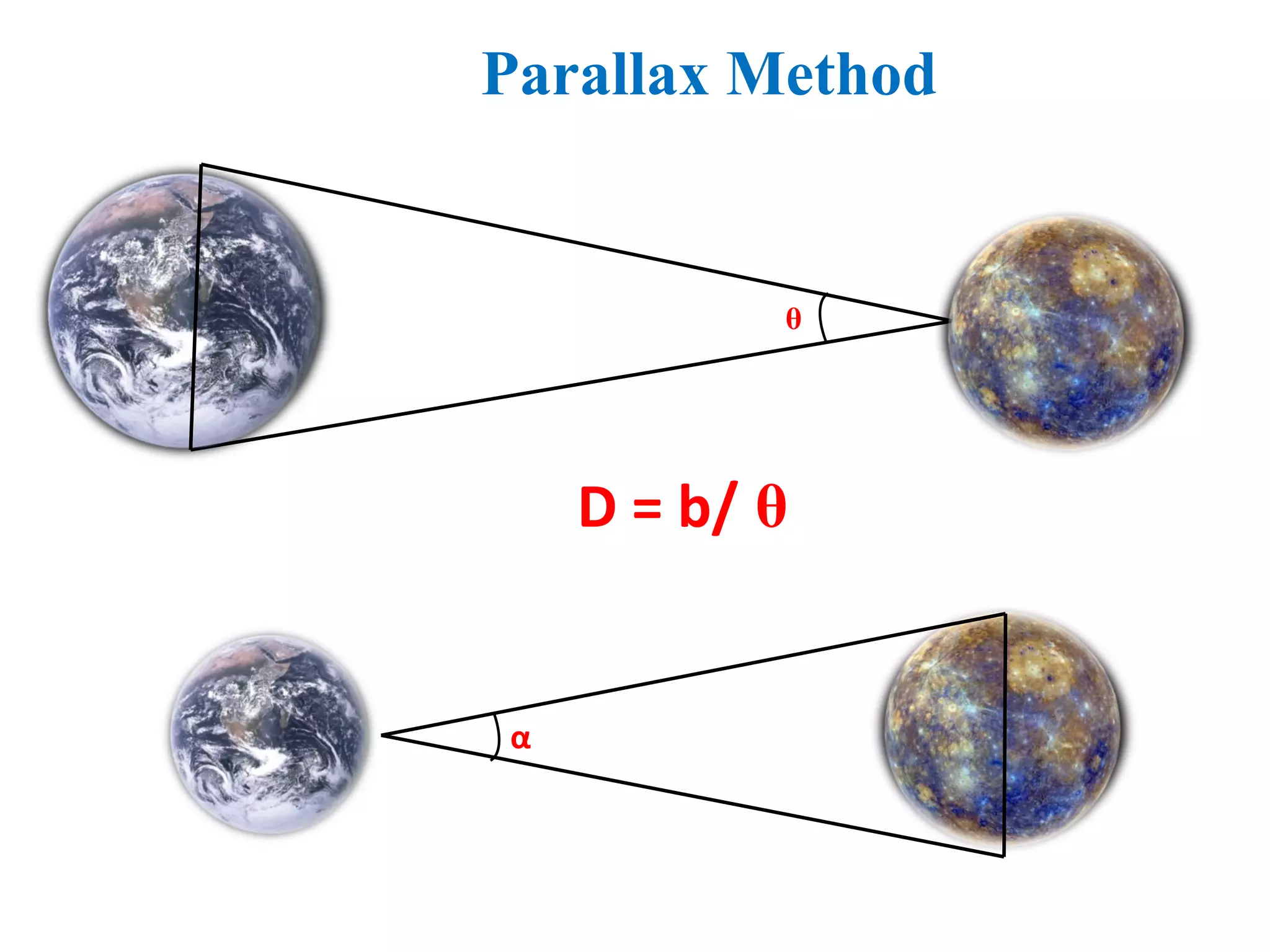
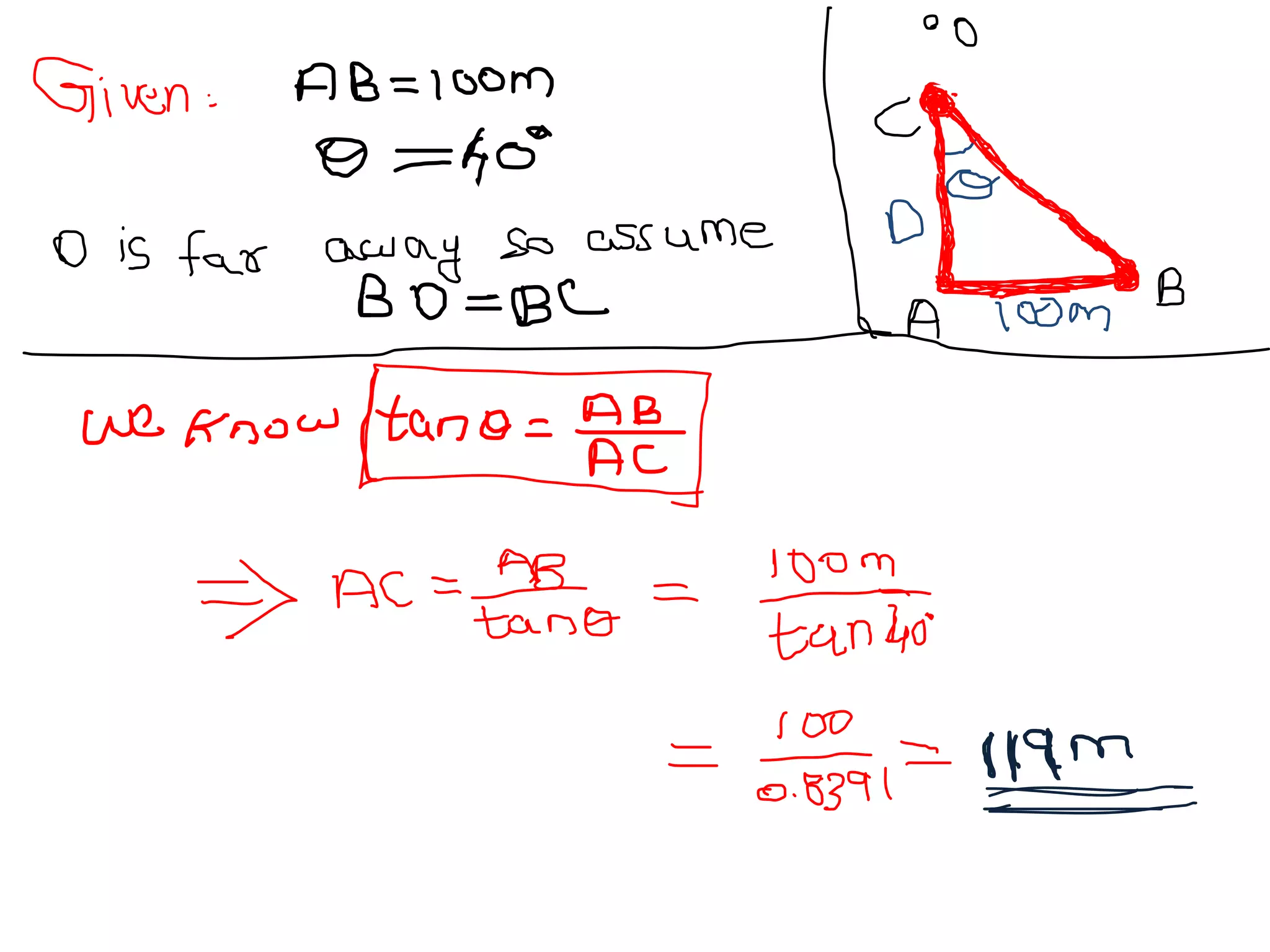
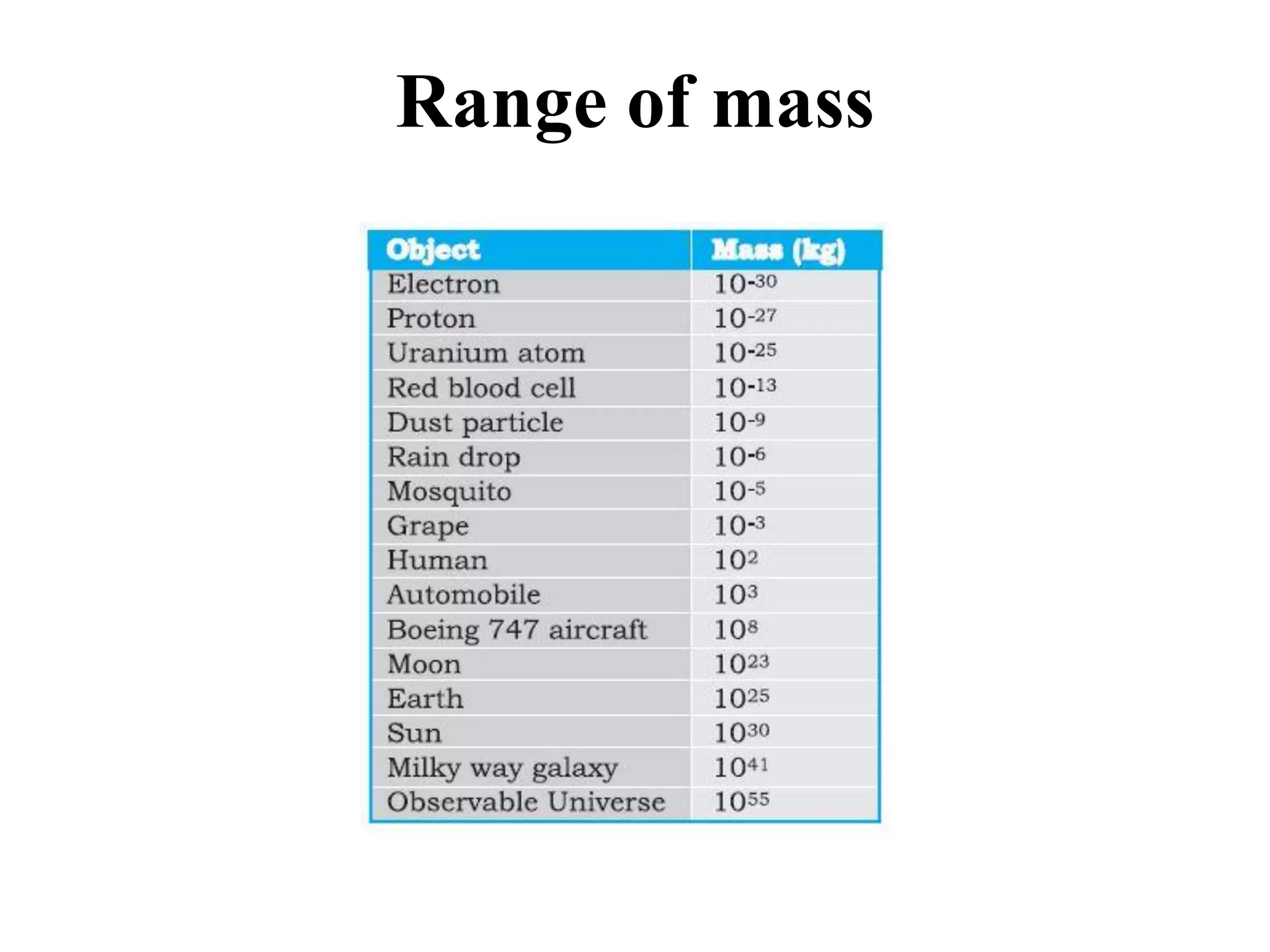
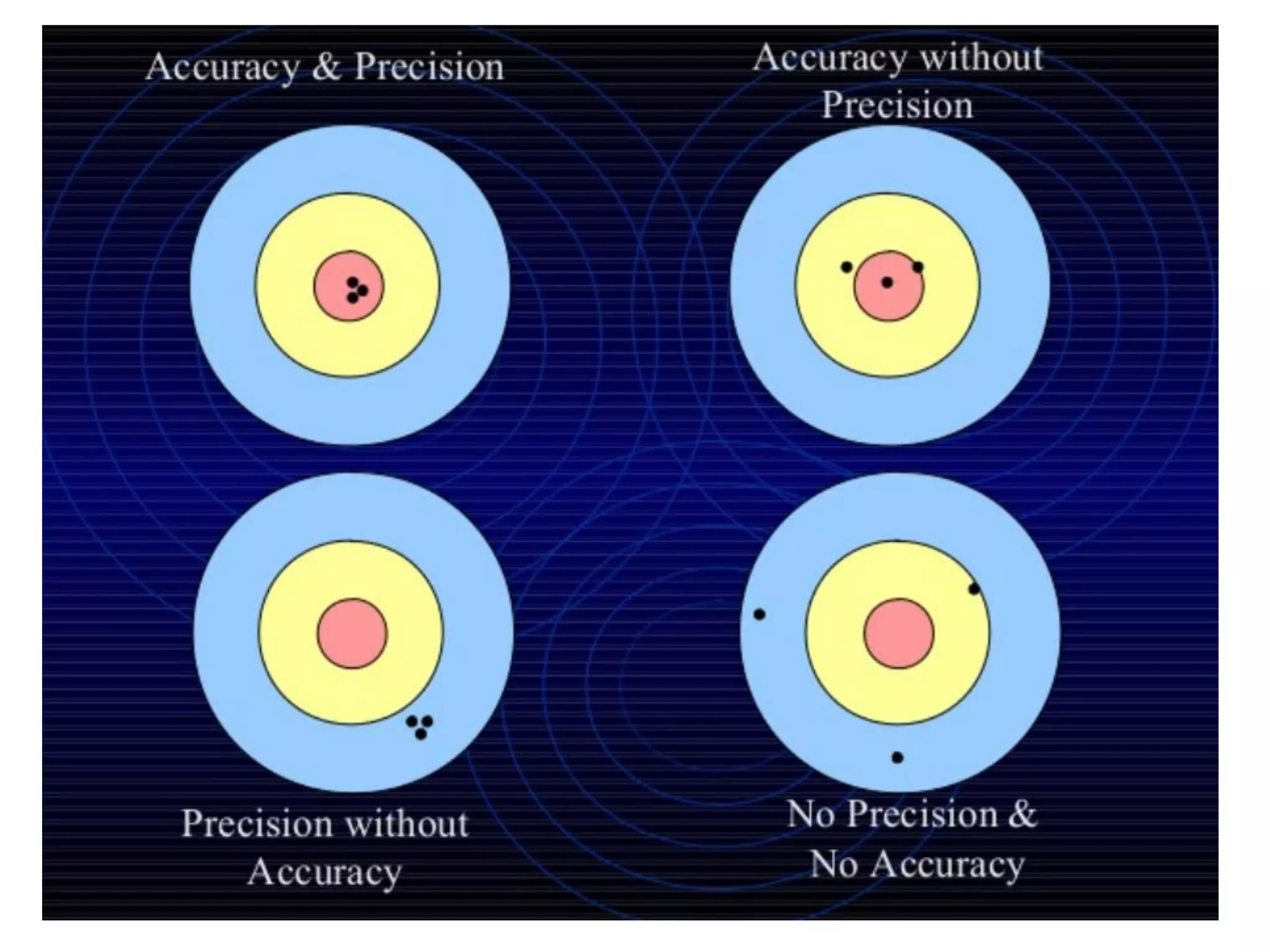
The document discusses the fundamental concepts of units and measurements in physics, explaining physical quantities, measurement systems, and types of errors. It defines fundamental and derived quantities, outlines different systems of units (CGS, FPS, MKS), and explains measurement methods for length, mass, and time, including the parallax method. Additionally, it covers accuracy, precision, types of errors, and the significance of dimensional analysis in ensuring consistency in measurements.

1. UNITS AND
MEASUREMENTS
PHYSICS
CLASS XI

2. PHYSICAL QUANITY
• Measurement of any physical quantity
involves comparison with a certain basic
arbitrarily chosen internationally accepted
reference standard called unit
• Any measurable quantity is called physical
quantity.
• Physical Quantity is of two types:
❑ Fundamental Quantity.
❑ Derived Quantity.

3. FUNDAMENTAL QUANTITY
• It is a physical quantity which is independent
of other physical quantity.
• Eg: Length, Mass , time….
DERIVED QUANTITY
❖ It is a physical quantity which depends upon
other physical quantities.
❖ Eg : acceleration, Area, Velocity…..
A complete set of both the base units and
derived units is known as System of Units

4. INTERNATIONAL SYSTEM OF UNITS
The base units for length, mass and time in these system are as follows.
❑ In CGS system they were centimeters, grams and seconds
respectively.
❑ In FPS system they were Foot, pound and second respectively.
❑ In MKS system they were meter, kilogram and second respectively.
International
system of
units
CGS FPS MKS

5. Measurement of Length
• Length can be measured directly using some of
the methods like using a vernier callipers for
length to an accuracy of 1/(10,000) or using a
meter scale for an accuracy of 1/1000.
• For measurements of length beyond this range
we use some indirect methods.
• One such method is parallax method, this
method is typically used to determine the
distance from earth to other planets.

6. Parallax method
• To measure the distance D of a far away planet
S by the parallax method we observe it from
two different positions A and B on the earth
separated by the distance AB = b.
• We measure the angle between the two
directions along which the planet is viewed at
these two points.
• The < ASB is represented by the symbol θ is
called the parallax angle or parallactic angle.

7. • After determining the distance D we can use a
similar method to calculate the size or angular
diameter of the planet.
• If d is the diameter of the planet and α Can be
measured from the same location on earth.

8. D = b/ θ
θ
α
Parallax Method

9. Q . A man wishes to estimate the distance of a
nearby tower from him. He stands at a point A
in front of the tower C and spots a very distant
object O in line with AC. He then walks
perpendicular to AC upto B, a distance of
100m and looks at O and C again. Since O is
very distant the direction BO is practically the
same as AO but he finds the line of sight of C
shifted from the original line of sight by an
angle θ =40° estimate the distance of the
tower C from the original position A

11. Q. The suns angular diameter is measured to be 1920”.
The distance D of the sun from the earth is 1.496×1011m.
What is the diameter of the sun.
Answer: The suns angular diameter α = 1920”
= 1920 × 4.85 × 10-6 rad.
= 9.31 × 10-3 rad
Suns diameter,
d = αD
= (9.31×10-3rad) × (1.496×1011m)
= 1.39 × 109 m

12. Range of Lengths

13. MEASUREMENT OF MASS
• Mass is a basic property of matter.
• The SI unit of mass is Kg.
• While dealing with the mass of atoms and
molecules Kg is inconvenient so we use another
unit called unified atomic mass unit(u).
• 1 unified mass = 1u
= (1/12) of the mass of an atom of
carbon -12 isotope including the mass of
electrons
= 1.66 × 10-27 kg

14. MEASUREMENT OF MASS
• Mass of commonly available objects can be
measured using a weighing machine used in
grocery shops.
• Large masses like mass of stars and planets can be
measured using Newton's law of gravitation
which will be discussed later on.
• Small masses like mass of atoms and molecules
can be measured using Mass Spectrograph in
which the radius of the trajectory is proportional
to the mass of a charged particle moving in
uniform electric and magnetic field.

15. Range of mass

16. MEASUREMENT OF TIME
• To measure any time interval we need a clock.
• We now use atomic standard of time.
• It is based on the periodic vibrations produced
in a caesium atom.
• This is the basis of the cesium clock
sometimes called atomic clock used in the
national standards.

17. ACCURACY AND PRECISION
• Accuracy is how close a measurement is to the
correct value for that measurement.
• The precision of a measurement system is
refers to how close the agreement is between
repeated measurements (which are repeated
under the same conditions).
• Measurements can be both accurate and
precise, accurate but not precise, precise but
not accurate, or neither.

19. ERRORS
• The results of any measurement from any
measuring instrument contains some
uncertainty. This uncertainty is called error.
• Thus every measurements is approximate due
to errors in measurements.
• In general errors is classified into three types:
❖ Systematic Errors
❖ Random Errors.

20. SYSTEMATIC ERRORS
• Systematic errors are those errors that tend to be
in one direction either positive or negative.
• Some of the sources of systematic errors are:
i. Instrumental Errors: This are errors that arise
from imperfect design or calibration of the
instrument it includes zero errors.
ii. Imperfection in experimental techniques or
procedure: External conditions acts as a factor
for measurement.
iii. Personal Errors: This are errors that arise due to
individuals bias, lack of proper setting of the
apparatus or individuals carelessness.

21. RANDOM ERROR
• This are errors that occur randomly and hence
are random with respect to sign and size.
• These can arise dues to random and
unpredictable fluctuations in experimental
conditions.
• For example when the same person repeats the
same observation it is very likely that he gets
different readings every time.

22. LEAST COUNT ERRORS
• The smallest value that can be measured by the
measuring instrument is called its least count.
• The least count error is the error associated with the
resolution of the instrument.
Eg: A vernier calliper has the least count of 0.01cm;
A spherometer may have a least count of 0.001cm .
• Least count errors can occur with both systematic and
random errors.
• Using instruments of higher precision, improving
experimental techniques .. Can reduce the least count
error.
• Repeating the observation several times and taking the
mean value of the observations can give you the result
very close to the true value of the measured quantity.

23. ABSOLUTE ERROR, RELATIVE
ERROR AND PERCENTAGE ERROR
• Absolute Error : The Magnitude of difference
between the individual measurements and the true
value of the quantity is called absolute error of the
measurement.
• Relative Error: It is the ratio of the mean absolute
error to the mean value of the quantity measured.
• Percentage Error: When relative error is
expressed in percent it is called percentage error.

25. ABSOLUTE ERROR, RELATIVE
ERROR AND PERCENTAGE ERROR
Q . We measure the time period of oscillation of a
simple pendulum. In successive measurements the
readings turn out to be 2.63s, 2.56s, 2.42s, 2.71s and
2.80s. Calculate the absolute error, relative error or
percentage error.
Solution :
Given : Successive measurement readings
= 2.63s, 2.56s, 2.42s, 2.71s and 2.80s.
Number of observations = 5

28. DIMENSIONS OF PHYSICAL
QUANITIES.

29. DIMENSIONAL ANALSYSIS AND
ITS APPLICATIONS
• The study of the relationship between physical quantities
with the help of dimensions and units of measurement is
termed as dimensional analysis.
• Dimensional analysis is essential because it keeps the units
the same, helping us perform mathematical calculations
smoothly.
• Dimensional analysis is a fundamental aspect of
measurement and is applied in real-life physics.
• We make use of dimensional analysis for three prominent
reasons:
– To check the consistency of a dimensional equation
– To derive the relation between physical quantities in physical
phenomena
– To change units from one system to another