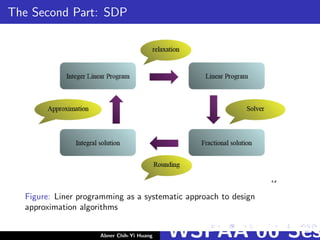
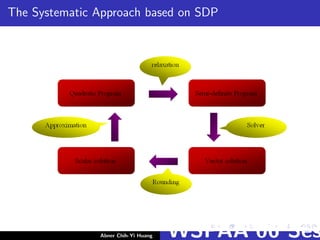
This document summarizes a presentation on derandomization techniques and semidefinite programming. It begins with an overview of derandomization using the method of conditional probabilities and a weighted MAXSAT algorithm example. It then discusses semidefinite programming, how it can solve certain problems more tightly than linear programming, and how it enables improved approximation algorithms, such as a 0.878 approximation for MAXCUT using a Goemans-Williamson random hyperplane rounding technique.











![Computation Tree for MAX Weighted SAT
To derandomize Program 2.10,
(1) At the i-th iteration, the random variable
mRWS (x|v1v2 · · · vi−1) means the measure of solution with
input x and the decided value vj of variable vj .
(2) If E[mRWS (x|v1v2 · · · vi−10)] ≤ E[mRWS (x|v1v2 · · · vi−11)],
then vi is set to 1, otherwise it is set to 0.
(3) Eventually, we have mA (x) = E[mRWS (x|v1v2 · · · vn)].
Abner Chih-Yi Huang WSPAA’06 Ses](https://image.slidesharecdn.com/moreonrandomization-semidefiniteprogrammingandderandomization-140510114426-phpapp01-150607173341-lva1-app6892/85/More-on-randomization-semi-definite-programming-and-derandomization-15-320.jpg)
![Computation Tree for MAX Weighted SAT
(4) At the i-th iteration, the random variable
mRWS (x|v1v2 · · · vi−1) means the measure of solution with
input x and the decided value vj of variable vj .
(5) If E[mRWS (x|v1v2 · · · vi−10)] ≤ E[mRWS (x|v1v2 · · · vi−11)],
then vi is set to 1, otherwise it is set to 0.
(6) Eventually, we have mA (x) = E[mRWS (x|v1v2 · · · vn)]
Assume that x contains t clauses c1, . . . , ct. We have
E[mRWS (x|v1v2 · · · vi−11)] =
t
j=1
w(cj )Pr{cj is satisfied|v1v2 · · · vi−11}
Abner Chih-Yi Huang WSPAA’06 Ses](https://image.slidesharecdn.com/moreonrandomization-semidefiniteprogrammingandderandomization-140510114426-phpapp01-150607173341-lva1-app6892/85/More-on-randomization-semi-definite-programming-and-derandomization-16-320.jpg)

![Computation Tree for MAX Weighted SAT
We have E[mRWS (x|v1v2 · · · vi−11)] =
Wi +
cj s.t. vi occurs +
w(cj )1 +
cj s.t. vi occurs -
w(cj )(1 −
1
2dj
)
Clearly it can be computed in P. Hence we have
E[mRWS (x)] ≤ E[mRWS (x|v1)]
≤ E[mRWS (x|v1v2)]
≤
...
≤ E[mRWS (x|v1 · · · vn)] = mA (x)
By Corollary 2.20, mA (x) ≥ E[mRWS (x)] ≥ m∗(x)/2
Abner Chih-Yi Huang WSPAA’06 Ses](https://image.slidesharecdn.com/moreonrandomization-semidefiniteprogrammingandderandomization-140510114426-phpapp01-150607173341-lva1-app6892/85/More-on-randomization-semi-definite-programming-and-derandomization-18-320.jpg)




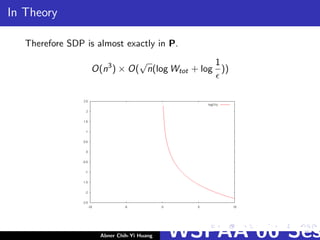
![In Theory and In Practice
In Theory : For worst-case complexity, the number of iterations to
solve a semidefinite program to a given accuracy grows with
problem size as O(n
1
2 ).
For example, [Alizadeh 1995] adapt Ye’s interior-point algorithm to
semidefinite programming performs O(
√
n(log Wtot + log 1
))
iterations and each iteration can be implemented in O(n3) time.
[Rendl et al. 1993].
Abner Chih-Yi Huang WSPAA’06 Ses](https://image.slidesharecdn.com/moreonrandomization-semidefiniteprogrammingandderandomization-140510114426-phpapp01-150607173341-lva1-app6892/85/More-on-randomization-semi-definite-programming-and-derandomization-24-320.jpg)
![In Practice
In Practice : the number of iterations required grows much
more slowly than n
1
2 , perhaps like log(n) or n
1
4 , and can often
be assumed to be almost constant. (5 to 50 iterations)
It is now generally accepted that interior-point methods for LPs are
competitive with the simplex method and even faster for problems
with more than 10,000 variables or constraints.[Lustig, et. al.,
1994]
Abner Chih-Yi Huang WSPAA’06 Ses](https://image.slidesharecdn.com/moreonrandomization-semidefiniteprogrammingandderandomization-140510114426-phpapp01-150607173341-lva1-app6892/85/More-on-randomization-semi-definite-programming-and-derandomization-26-320.jpg)








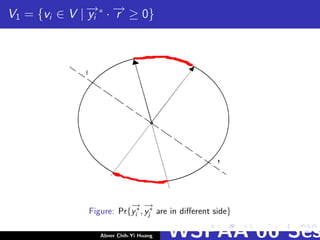
![Analysis of Algorithm
Denote mRWC (x) be the measure of the solution returned by
program 5.3. If −→r divide the circle into two sides.
E[mRWC (x)] =
n
j=1
j
i=1
wij Pr{
−→
y∗
i ,
−→
y∗
j are in different side}
The probability Pr{
−→
y∗
i ,
−→
y∗
j are in different side} is the segments of
the circle that
−→
y∗
i ,
−→
y∗
j dominated.
2
cos−1(−→yi
∗ ·
−→
y∗
j )
2π
=
cos−1(−→yi
∗ ·
−→
y∗
j )
π
(polar-coordinate)
Abner Chih-Yi Huang WSPAA’06 Ses](https://image.slidesharecdn.com/moreonrandomization-semidefiniteprogrammingandderandomization-140510114426-phpapp01-150607173341-lva1-app6892/85/More-on-randomization-semi-definite-programming-and-derandomization-37-320.jpg)
![Analysis of Algorithm
Compare
E[mRWC (x)] =
n
j=1
j
i=1
wij
cos−1(−→yi
∗ ·
−→
y∗
j )
π
m∗
QP−CUT (x) =
1
2
n
j=1
j
i=1
wij (1 − −→yi · −→yj )
We have
E[mRWC (x)] =
2 cos−1(−→yi
∗ ·
−→
y∗
j )
π(1 − cos(cos−1(−→yi
∗ ·
−→
y∗
j ))
1
2
n
j=1
j
i=1
wij (1 − −→yi · −→yj )
Abner Chih-Yi Huang WSPAA’06 Ses](https://image.slidesharecdn.com/moreonrandomization-semidefiniteprogrammingandderandomization-140510114426-phpapp01-150607173341-lva1-app6892/85/More-on-randomization-semi-definite-programming-and-derandomization-39-320.jpg)
![Analysis of Algorithm
Let β = min0<α≤π
2α
π(1−cos(α) , Since QP-CUT(x) is a relaxation of
IQP-CUT(x), we have
E[mRWC (x)] ≥ β ×m∗
QP−CUT (x) ≥ β ×m∗
IQP−CUT (x) = β ×m∗
(x)
By Lemma, β > 0.8785. Thus, this algorithm is
1.139-approximation algorithm.
Abner Chih-Yi Huang WSPAA’06 Ses](https://image.slidesharecdn.com/moreonrandomization-semidefiniteprogrammingandderandomization-140510114426-phpapp01-150607173341-lva1-app6892/85/More-on-randomization-semi-definite-programming-and-derandomization-40-320.jpg)





![Improved Algorithm for Weighted 2-SAT
Observe that, for two literals clause,
t(cj ) = 1 − t(vi ∨ vk) = 1 − t(vi )t(vk)
= 1 −
1 − yi y0
2
1 − yky0
2
=
1
4
[(1 + yi y0) + (1 + 1 − yky0) + (1 − yi yk)]
Other cases are similar. For example, let c3 = y1 + y2, if
y1 = 1, y2 = −1,
t(c3) =
1
4
[(1 + y1y0) + (1 + y2y0) + (1 − y1y2)]
=
1
4
[(1 + 1) + (1 + (−1)) + (1 − (−1))]
=
4
4
= 1
Abner Chih-Yi Huang WSPAA’06 Ses](https://image.slidesharecdn.com/moreonrandomization-semidefiniteprogrammingandderandomization-140510114426-phpapp01-150607173341-lva1-app6892/85/More-on-randomization-semi-definite-programming-and-derandomization-46-320.jpg)
![Improved Algorithm for Weighted 2-SAT
It could be expressed as following,
maximize n
j=0
j−1
i=0[aij (1 − yi yj ) + bij (1 + yi yj )]
subject to yi ∈ {−1, 1} i = 0, 1, · · · , n
where y0 is TRUE, i.e., yi = y0. We can relax it to
maximize n
j=0
j−1
i=0[aij (1 − vi vj ) + bij (1 + vi vj )]
subject to vi ∈ Sn vi ∈ V .
Abner Chih-Yi Huang WSPAA’06 Ses](https://image.slidesharecdn.com/moreonrandomization-semidefiniteprogrammingandderandomization-140510114426-phpapp01-150607173341-lva1-app6892/85/More-on-randomization-semi-definite-programming-and-derandomization-47-320.jpg)
![Improved Algorithm for Weighted 2-SAT
We have
E[V ] = 2
n
j=0
j−1
i=0
aij Pr{vi , vj are in different sides.}
+
n
j=0
j−1
i=0
bij Pr{vi , vj are in different sides.}
Recall the analysis of Max. Weighted Cut. It shows that by similar
method, we can get the expected performance ratio is at most
1.139.
Abner Chih-Yi Huang WSPAA’06 Ses](https://image.slidesharecdn.com/moreonrandomization-semidefiniteprogrammingandderandomization-140510114426-phpapp01-150607173341-lva1-app6892/85/More-on-randomization-semi-definite-programming-and-derandomization-48-320.jpg)
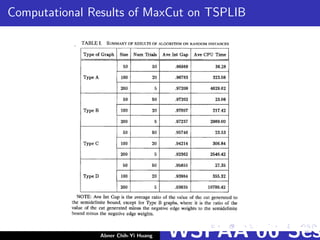
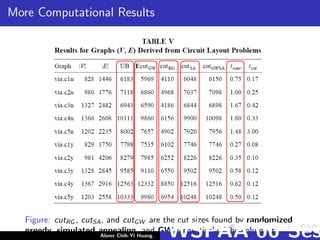
![More Computational Results
[Homer, et. al., 1997] have implemented our algorithm on a CM-5,
and have shown that it produces optimal or very nearly optimal
solutions to a number of MAX CUT instances derived from via
minimization problems.
Abner Chih-Yi Huang WSPAA’06 Ses](https://image.slidesharecdn.com/moreonrandomization-semidefiniteprogrammingandderandomization-140510114426-phpapp01-150607173341-lva1-app6892/85/More-on-randomization-semi-definite-programming-and-derandomization-50-320.jpg)