The document discusses algorithms for computing market equilibria in economic models. It introduces Fisher's model and the Arrow-Debreu model of markets. It describes how competitive equilibria and Pareto efficiency arise in these models under certain assumptions. The document then presents an algorithm based on a primal-dual approach that computes market clearing prices for Fisher's linear model in polynomial time by incrementally raising prices until surplus is eliminated.

1. Introduction
Algorithms
Discussion and Open Problems
Introduction to Algorithmic Aspect of Market
Equilibria
Abner Chih Yi Huang
March 26, 2009
CSBB Lab, CS, NTHU
1 / 67

2. Introduction
Algorithms
Discussion and Open Problems
Materials
Vijay V. Vazirani, chapter 5, Algorithmic Game Theory,
Cambridge University Press, 2008.[5]
Devanur, et al., Market Equilibrium via a Primal-Dual-Type
Algorithm, FOCS’02, 389-395.[1]
Devanur, et al., Market equilibrium via a primal–dual
algorithm for a convex program, J. ACM, 2008, v. 55,
pp.1-18[2]
2 / 67

3. Introduction
Algorithms
Discussion and Open Problems
Terminology
Market?
Fisher’s model, 1891
Arrow-Debreu model, 1954
Efficiency?
Equilibria? Existence?
3 / 67

4. Introduction
Algorithms
Discussion and Open Problems
Fisher’s model
n buyers, with specified money, m(i) for buyer i
k goods (unit amount of each good)
Linear utilities (效用/爽度): ui,j is utility derived by i on
obtaining one unit of j. Total utility of buyer i,
ui =
j
ui,jxi,j
4 / 67

5. Introduction
Algorithms
Discussion and Open Problems
Arrow-Debreu model
n buyers, k goods (unit amount of each good)
Linear utilities : ui,j is utility derived by i on obtaining one
unit of j. Total utility of buyer i,
ui =
j
ui,jxi,j
The Arrow-Debreu model is also known as the Walrasian
model or the exchange model (以物易物), and it generalizes
Fisher’s model.
5 / 67

6. Introduction
Algorithms
Discussion and Open Problems
Pareto improvement, 1886
Definition
Given a set of alternative allocations of, say, goods or income for a
set of individuals, a movement from one allocation to another that
can make at least one individual better off without making any
other individual worse off is called a Pareto improvement.
Definition
An allocation is Pareto efficient or Pareto optimal when no further
Pareto improvements can be made. This is often called a strong
Pareto optimum (SPO).
6 / 67

7. Introduction
Algorithms
Discussion and Open Problems
Market-Clearing Price
Definition
The price at Market equilibrium is often called the equilibrium
price or market clearing price and will tend not to change unless
demand or supply change.
Figure: The price at Market equilibrium
7 / 67

8. Introduction
Algorithms
Discussion and Open Problems
Market Models Have Equilibria
Definition
A competitive equilibrium is a market, for Fisher’s model or
Arrow-Debreu model, with the following assumptions.
complete markets
No Uncertainty, i.e., we can calculate the future
deterministically.
perfect competition
All information are available, i.e., preferences and budgets, are
public.
Zero transaction cost
local nonsatiation of preferences
preference function are continuous and strictly increasing in all
goods, i.e., more is better.
8 / 67

9. Introduction
Algorithms
Discussion and Open Problems
First Fundamental Theorem of Welfare Economics
Theorem (Arrow-Debreu, 1954)
Any competitive equilibrium or Walrasian equilibrium leads to an
Pareto efficient allocation of resources.
In other words,
Theorem (Adam Smith’s invisible hand)
That competitive markets tend toward the efficient allocation of
resources.
9 / 67

10. Introduction
Algorithms
Discussion and Open Problems
Combinatorial Algorithm for Fisher’s Model
Problem
Given a market of Fisher’s model, what is the market equilibria? In
the other words, what is the price such that the total utility of all
people in this market is maximum?
INPUT: Linear utility functions of buyers, integral money of
buyers, divisible goods.
OUTPUT: The prices of goods.
Measurement: Total utilities.
10 / 67

11. Introduction
Algorithms
Discussion and Open Problems
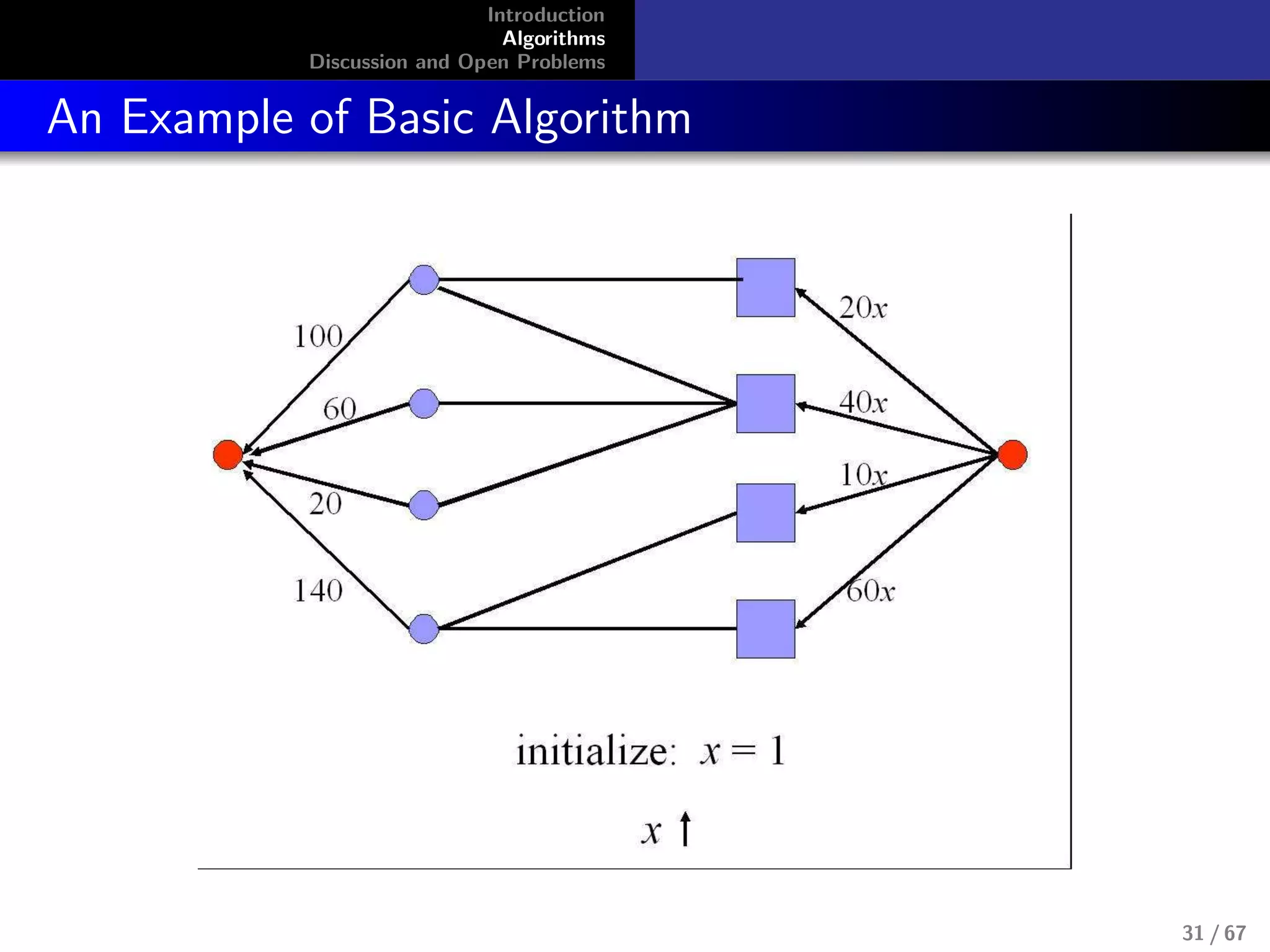
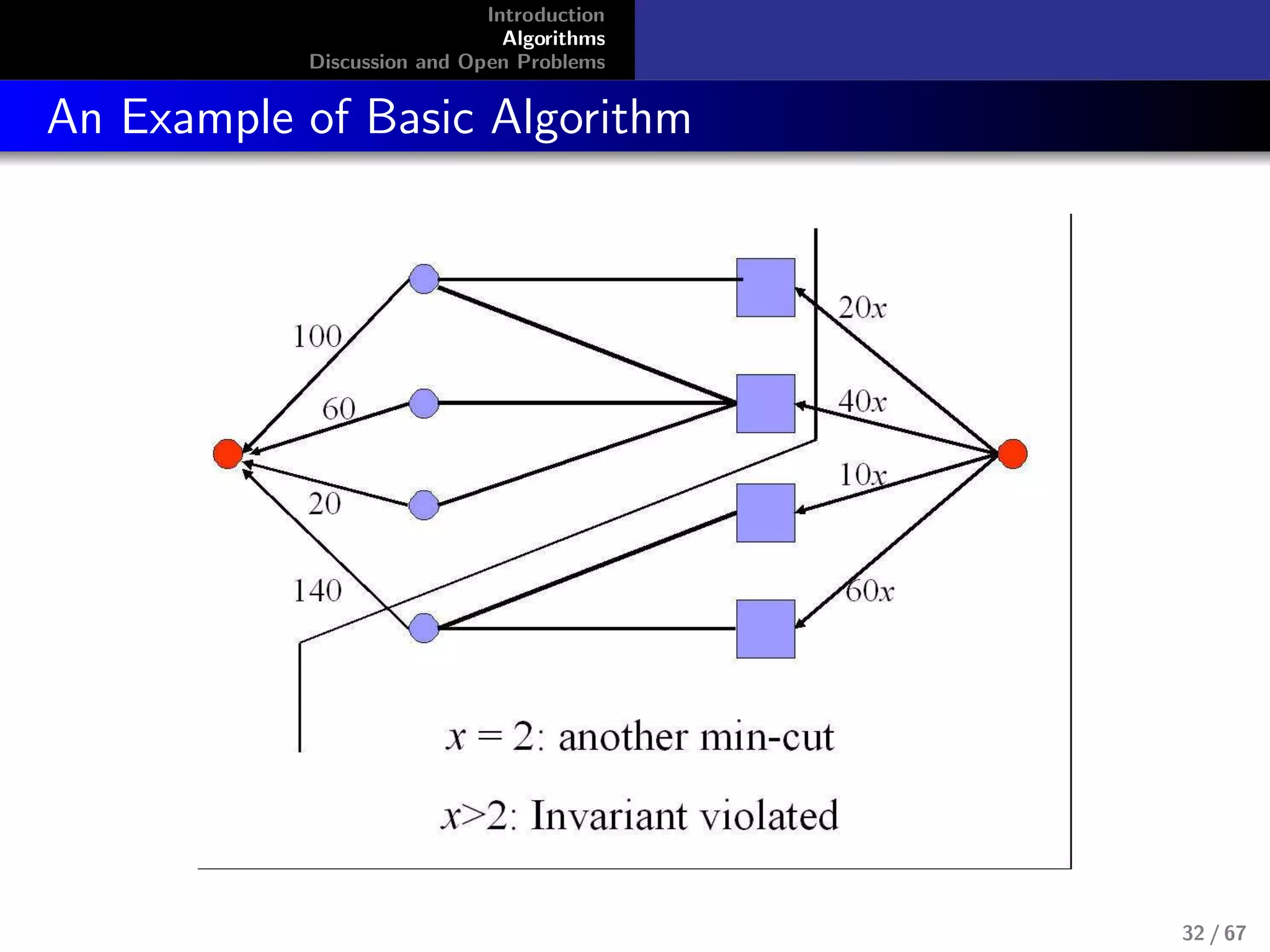
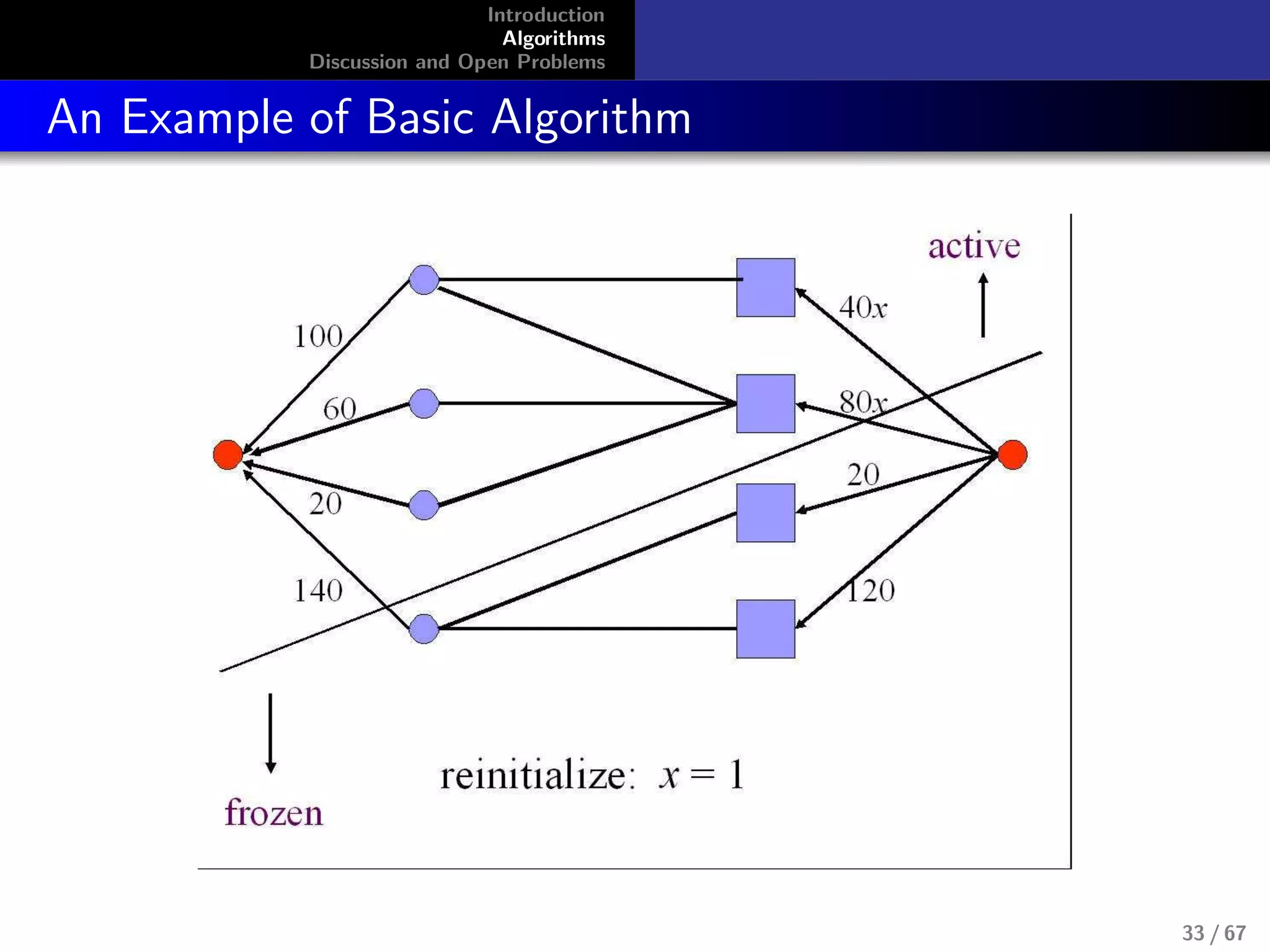
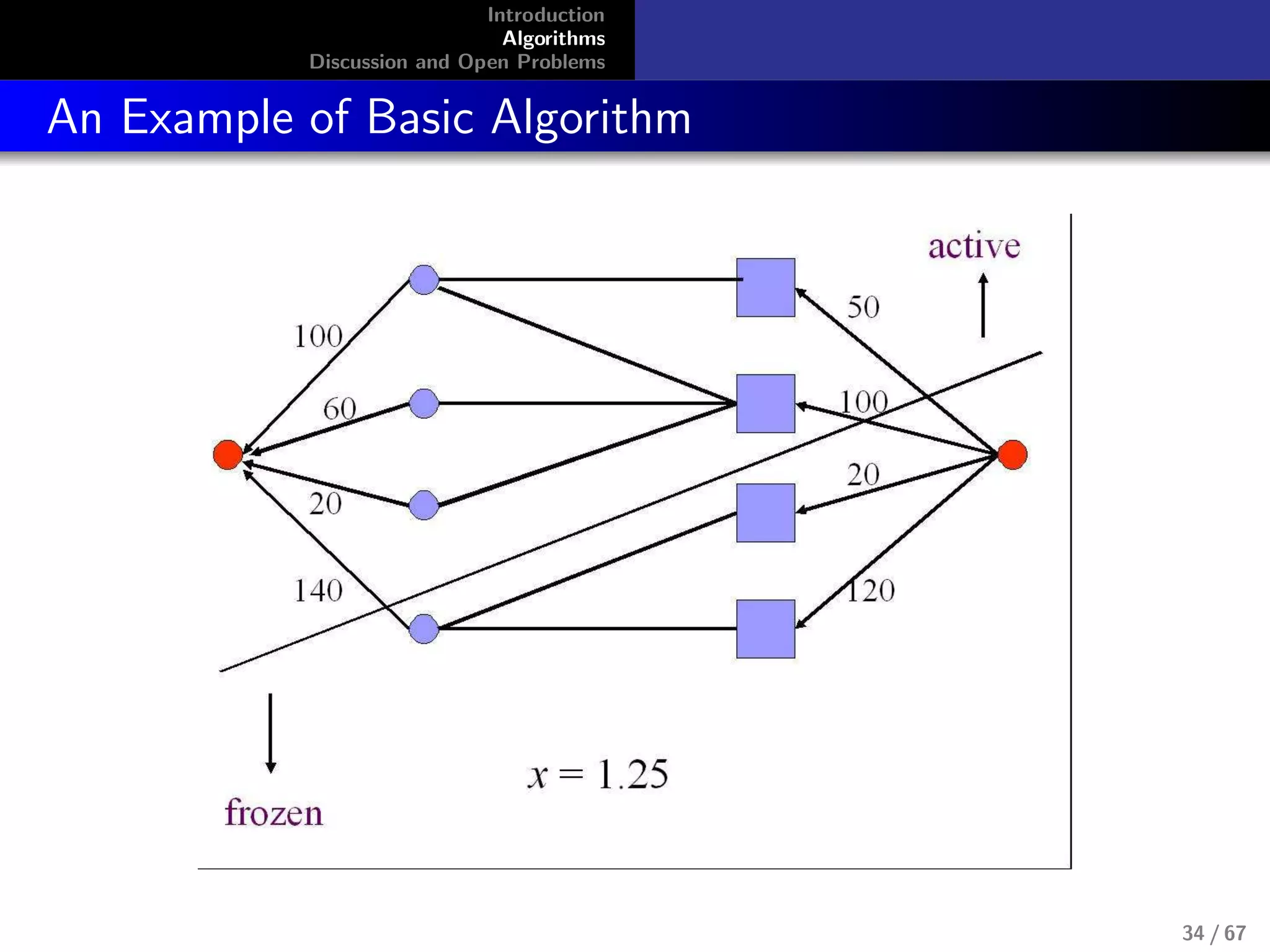
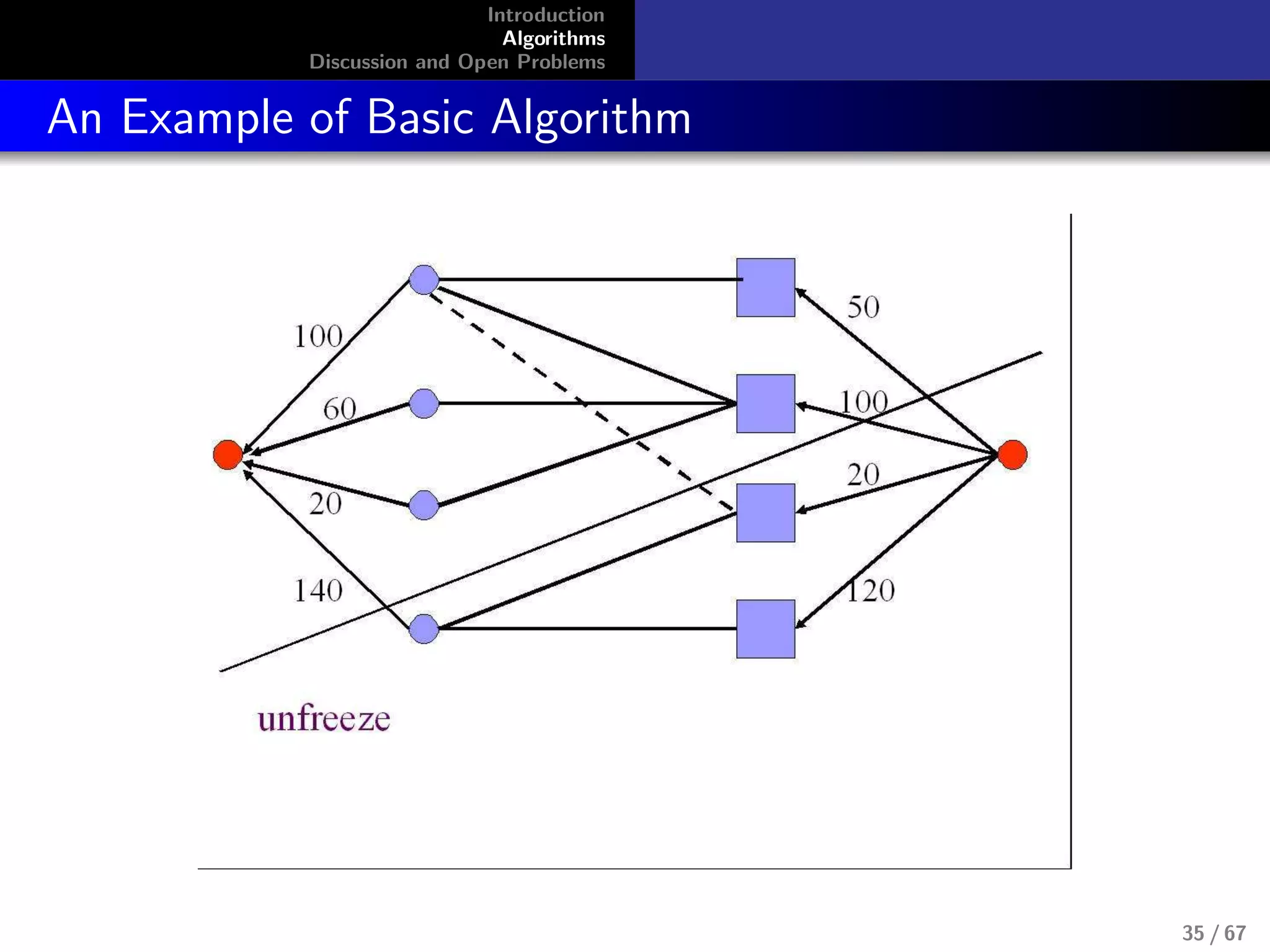
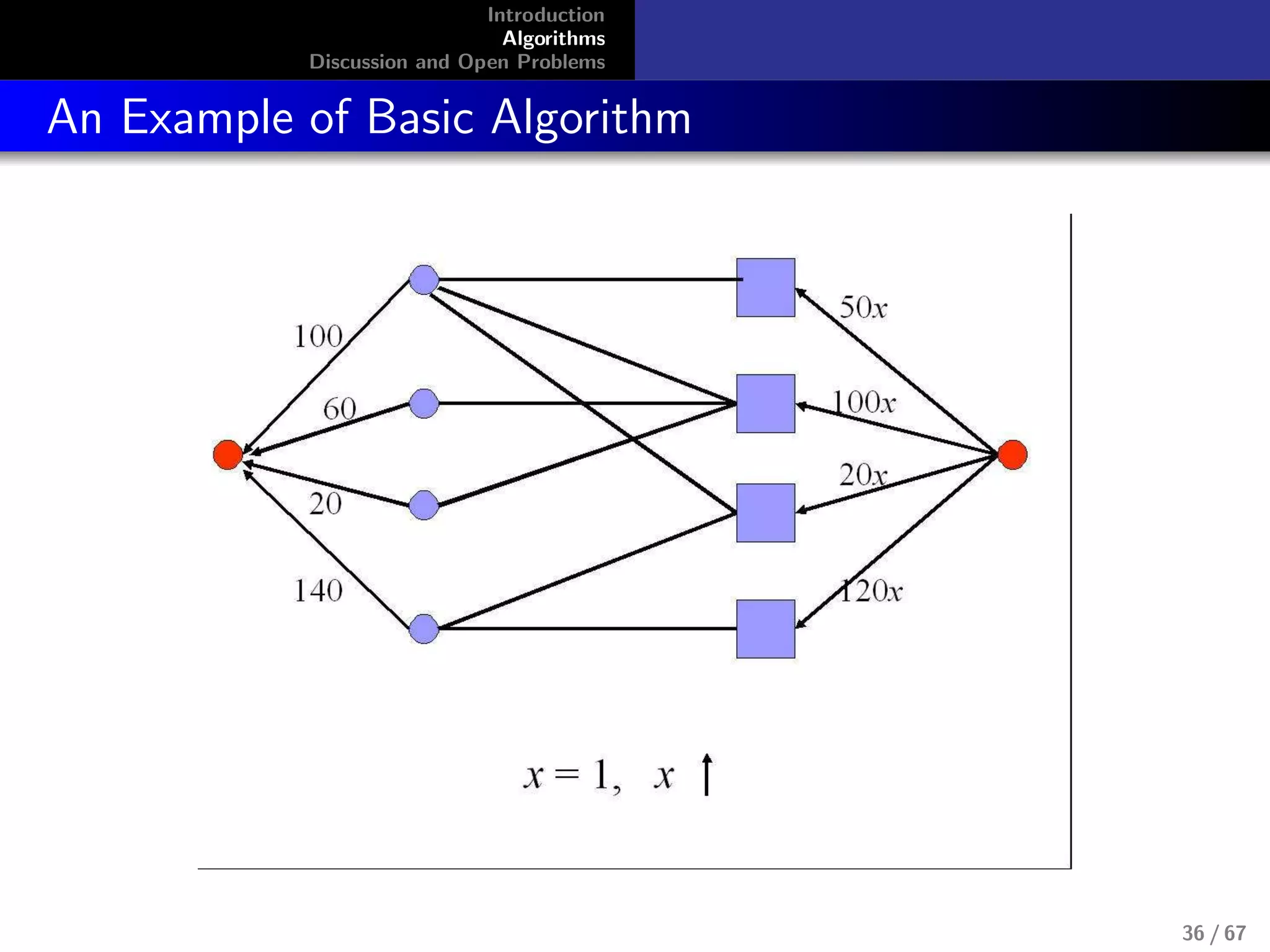
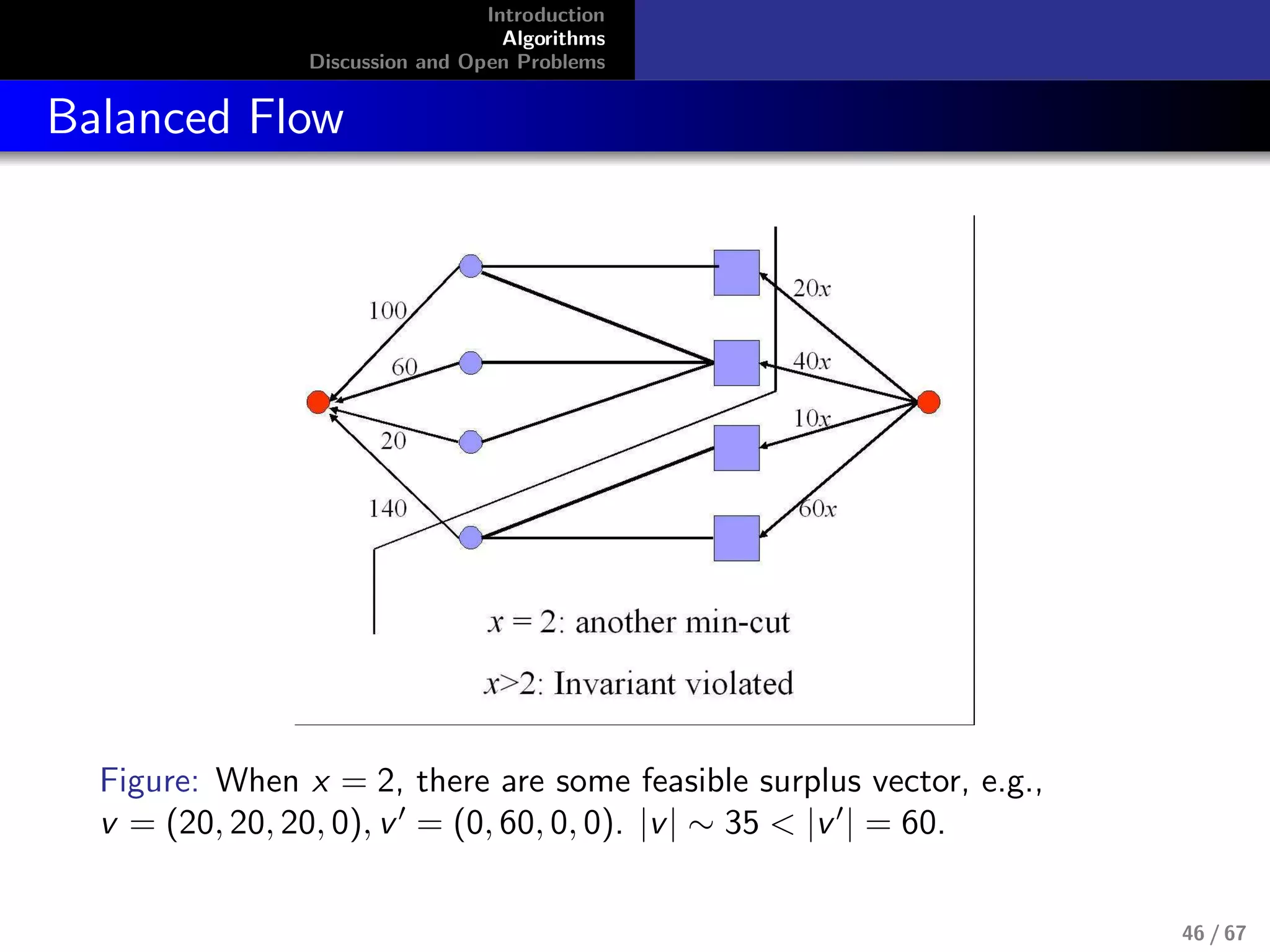
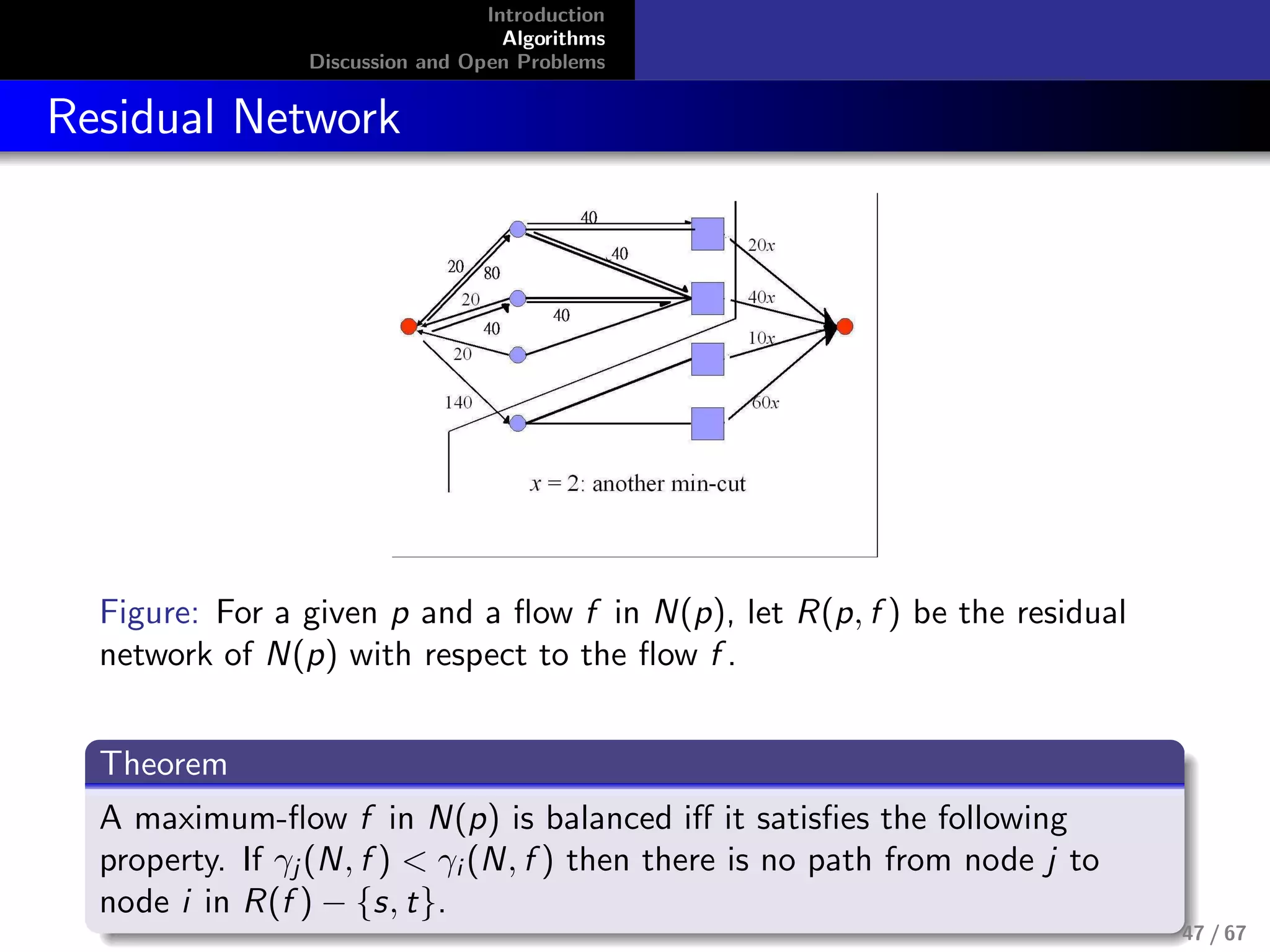
Combinatorial Algorithm for Fisher’s Model
No LP’s known for capturing equilibrium
allocations for Fisher’s model, although this
model doesn’t require integer constraints.
max
i
ui , s.t.,
j
pj xi,j ≤ mi , ui =
j
ui,jxi,j
Devanur, Papadimitriou, Saberi, and Vazirani,
2002[1]
Use primal-dual schema. It is highly successful algorithm
design technique from exact and approximation algorithms
11 / 67

12. Introduction
Algorithms
Discussion and Open Problems
Combinatorial Algorithm for Fisher’s Model
Ask firstly: Given prices p,
are they equilibrium prices?
12 / 67

13. Introduction
Algorithms
Discussion and Open Problems
Reduce It to Assignment Problem
Figure: An edge exists if and only if it produce maximum utilities ratio.
13 / 67

14. Introduction
Algorithms
Discussion and Open Problems
Example of Building Equality Graph N(p)
Figure: The 4-tuple of each buyer means the linear coefficients of utility
function, i.e., (ui,1, ui,2, ui,3, ui,4).
14 / 67

15. Introduction
Algorithms
Discussion and Open Problems
Example of Building Equality Graph N(p)
Figure: For buyer 1, we have
ui,1
p1
= 1
25 ,
ui,2
p2
= 1
5 ,
ui,3
p3
= 1
2 ,
ui,4
p4
= 2
9 . Hence
we can connect 1, 3 by an edge.
15 / 67

16. Introduction
Algorithms
Discussion and Open Problems
Example of Building Equality Graph N(p)
Figure: Build N(p) by similar way.
16 / 67

17. Introduction
Algorithms
Discussion and Open Problems
Reduce It to Maximal Flow Problem
Figure: Hence, we can construct the network of p, which is denoted by
N(p), if p is given.
17 / 67

18. Introduction
Algorithms
Discussion and Open Problems
A Verifying Algorithm of Market Clearing Prices
Theorem
The price p is equilibrium prices iff in the network N(p) the two
cuts (s, A ∪ B ∪ t) and (s ∪ A ∪ B, t) are min-cuts. If so, allocations
corresponding to any max-flow in N are equilibrium allocations.
18 / 67

19. Introduction
Algorithms
Discussion and Open Problems
Computing Market Clearing Prices for Linear Fisher Model
Now we have a verifier.
Could we devise an algorithm to compute
Market Clearing Prices for Linear Fisher
Model?
19 / 67

20. Introduction
Algorithms
Discussion and Open Problems
Idea of Algorithm
”primal” variables: allocations
”dual” variables: prices of goods
Approach equilibrium prices from below:
start with very low prices;
buyers have surplus money iteratively.
Keep raising prices and decreasing surplus.
i.e., iterations of executing primal & dual
improvements
20 / 67

21. Introduction
Algorithms
Discussion and Open Problems
Recall: maximum-flow problem
FORD-FULKERSON Method costs O(|E||f ∗|).
Find augmenting path repeatedly.
Augmenting path with better property is critical!
Edmonds-Karp algorithm runs in O(|V ||E|2) time.
21 / 67

22. Introduction
Algorithms
Discussion and Open Problems
Invariant 1
Invariant 1
Let A, B denote goods and buyers respectively. The
prices p are such that (s, A ∪ B ∪ t) is a min-cut in
N(p).
The Invariant ensures that, at current prices, all
goods can be sold. The only eventuality is that
buyers may be left with surplus money. When the
surplus vanishes, market clearing prices have been
attained.
22 / 67

23. Introduction
Algorithms
Discussion and Open Problems
Invariant 1
Definition
Let A, B denote goods and buyers respectively. For S ⊆ B, define
its money flow mf (S) = i∈S m(i). For S ⊆ A, define its money
flow mf (S) = i∈S p(i).
Definition
Let Γ(S) denote the neighborhood in the bipartite graphs
G(A, B, E).
Lemma
For given prices p network N(p) satisfies the Invariant 1 iff.
∀S ⊆ A, mf (S) ≤ mf (Γ(S))
23 / 67

24. Introduction
Algorithms
Discussion and Open Problems
An Example
24 / 67

25. Introduction
Algorithms
Discussion and Open Problems
Invariant 1
If the Invariant 1 holds, it is easy to see that
there is a unique maximal set S ⊆ A such that
mf (S) = mf (Γ(S)).
(S, Γ(S)) is the tight set w.r.t. prices p.
The subgraph induced by (S, Γ(S)) is named
frozen subgraph.
The active subgraph is the induced
subgraph of G by (A − S, B − Γ(S)).
25 / 67

26. Introduction
Algorithms
Discussion and Open Problems
Lemma
Lemma
If the Invariant 1 holds and S ⊆ A is the tight set,
then each good j ∈ (A − S) has an edge, in the
graph N(p), to some buyer i ∈ (B − Γ(S)).
Consider a buyer j ∈ (A − S). If all edges of j
incident to Γ(S), then
mf (S ∪ j) > mf (S) = mf (Γ(S)) = mf (Γ(S ∪ j)).
26 / 67

27. Introduction
Algorithms
Discussion and Open Problems
Physical Meaning of Invariant 1
Consider the set S such that mf (S) = mf (Γ(S)).
Tight set S means p(Γ(S)) are equilibrium prices of the
sub-market. It is Pareto optimum, since the prices of goods in
the tight set cannot be increased without violating the
Invariant 1.
27 / 67

28. Introduction
Algorithms
Discussion and Open Problems
Physical Meaning of Invariant 1
The active subgraph implies that the prices of goods 3, 4 are
too high to buyer 4.
Hence sellers need to reduce prices.
Note that we can avoid this case by starting with very low
prices.
Another case is the prices of goods 3, 4 are too low to buyer
4. Seller just raise the prices.
28 / 67

29. Introduction
Algorithms
Discussion and Open Problems
Basic Algorithm
29 / 67

30. Introduction
Algorithms
Discussion and Open Problems
Basic Algorithm
We would like to raise prices of goods in the active
subgraph in such a way that the equality edges in it
are retained. The algorithm raises x, starting with
x = 1, until one of the following happens:
Event 1: A set R = ∅ goes tight in the active
subgraph.
Event 2: An new equality edge from goods in S
to buyers outside the tight set.
30 / 67

31. Introduction
Algorithms
Discussion and Open Problems
An Example of Basic Algorithm
31 / 67

32. Introduction
Algorithms
Discussion and Open Problems
An Example of Basic Algorithm
32 / 67

33. Introduction
Algorithms
Discussion and Open Problems
An Example of Basic Algorithm
33 / 67

34. Introduction
Algorithms
Discussion and Open Problems
An Example of Basic Algorithm
34 / 67

35. Introduction
Algorithms
Discussion and Open Problems
An Example of Basic Algorithm
35 / 67

36. Introduction
Algorithms
Discussion and Open Problems
An Example of Basic Algorithm
36 / 67

37. Introduction
Algorithms
Discussion and Open Problems
Basic Algorithm
Hence, there is an intuitive approach to solve
this problem by raising the prices of goods in
A − S until arriving the goal.
Like the idea of FORD-FULKERSON Method, it
will increase the utilities by finding tight sets
until the only tight set is (A, B).
We skip the details of finding the tight set. (p.
61)
37 / 67

38. Introduction
Algorithms
Discussion and Open Problems
Time Complexity of Basic Algorithm
Basic algorithm is to solve this problem by raising the
prices of goods in A − S until arriving the goal.
The execution sequence:
↑, ↑, ↑, E1, ↑, ↑, E2, ↑, E1, ↑, E2, ↑, ↑, ↑, ↑, E2, ↑, · · ·
We can divide it into phases.
↑, ↑, ↑, E1
Phase 1
, ↑, ↑, E2, ↑, E1
Phase 2
, ↑, E2, ↑, ↑, ↑, ↑, E2, ↑, · · ·
···
Each phase is partitioned into iterations which conclude
with a new edge entering the equality subgraph.
38 / 67

39. Introduction
Algorithms
Discussion and Open Problems
Time Complexity of Basic Algorithm
Let M be the total money possessed by the
buyers and let f be the max-flow computed in
network N(p) at current prices p. Thus M − f
is the surplus money with the buyers.
Let U = maxi,j{ui,j} and let ∆ = nUn
.
Lemma
At the termination of a phase, the prices of goods in
the newly tight set must be rational numbers with
denominator ≤ ∆.
39 / 67

40. Introduction
Algorithms
Discussion and Open Problems
Time Complexity of Basic Algorithm
Lemma
At the termination of a phase, the prices of goods in the newly
tight set must be rational numbers with denominator ≤ ∆.
Figure: Consider the newly tight set (S, Γ(S)) as a connected bipartite
graph. We can derive mf (S) = pj c/d ⇒ pj = mf (Γ(S))d/c.
40 / 67

41. Introduction
Algorithms
Discussion and Open Problems
Time Complexity of Basic Algorithm
Lemma
Each phase consists of at most n iterations.
Lemma
Consider two phases P and P , not necessarily
consecutive, such that good j lies in the newly tight
sets at the end of P as well as P . Then the increase
in the price of j, going from P to P , is ≥ 1/∆2
.
41 / 67

42. Introduction
Algorithms
Discussion and Open Problems
Time Complexity of Basic Algorithm
lemma
tight set can be found using n max-flow computations.
Lemma
Basic Algorithm terminates with market clearing prices in at
most M∆2
phases, and executes O(Mn2
∆2
) max-flow
computations.
No one discovered a technique to bound the running time
in P of this approach.
42 / 67

43. Introduction
Algorithms
Discussion and Open Problems
Recall: Maximum-Flow problem
Figure: FORD-FULKERSON Method is not in P. Edmonds-Karp
algorithm runs in O(|V ||E|2
) time by finding better augmenting path.
How do we ensure that the surplus money of buyers
reduces fast enough that the algorithm terminates
in polynomial time?
43 / 67

44. Introduction
Algorithms
Discussion and Open Problems
Establishing polynomial running time
Like Maximal-Flow problem, the method of finding improvement
solution is critical. The authors proposed a method named
balanced flow.
For a given flow f in the network N(p), define the surplus of buyer
i, γ(p, f ), to be the residual capacity of the edge (i, t) with
respect to f , which is equal to mi minus the flow sent through the
edge (i, t).
Define the surplus vector
γ(p, f ) := (γ1(p, f ), γ2(p, f ), · · · , γn(p, f ))
Let |v| denote the l2 norm of vector v.
44 / 67

45. Introduction
Algorithms
Discussion and Open Problems
Balanced Flow
Definition
For any given p, a maximum flow that minimizes
|γ(p, f )| over all choices of f is called a balanced
flow. If |γ(p, f )| < |γ(p, f )|, then we say f is more
balanced than f .
Lemma
All balanced flows in N(p) have the same surplus
vector.
45 / 67

46. Introduction
Algorithms
Discussion and Open Problems
Balanced Flow
Figure: When x = 2, there are some feasible surplus vector, e.g.,
v = (20, 20, 20, 0), v = (0, 60, 0, 0). |v| ∼ 35 < |v | = 60.
46 / 67

47. Introduction
Algorithms
Discussion and Open Problems
Residual Network
Figure: For a given p and a flow f in N(p), let R(p, f ) be the residual
network of N(p) with respect to the flow f .
Theorem
A maximum-flow f in N(p) is balanced iff it satisfies the following
property. If γj (N, f ) < γi (N, f ) then there is no path from node j to
node i in R(f ) − {s, t}.
47 / 67

48. Introduction
Algorithms
Discussion and Open Problems
Balanced Flow
Figure: Circulation is impossible.
48 / 67

49. Introduction
Algorithms
Discussion and Open Problems
The Improved algorithm
Figure: Here we skip the detial to find balanced flow. (p.64) 49 / 67

50. Introduction
Algorithms
Discussion and Open Problems
Time Complexity Analysis
Lemma
The number of iterations executed in a phase is at
most n. Moreover, in every phase, there is an
iteration in which surplus of at least one of the
vertices is reduced by at least δ
n.
Lemma
If p0 and p∗
are surplus vectors before and after a
phase, |p∗
|2
≤ |p0|2
(1 − 1
n2 ).
50 / 67

51. Introduction
Algorithms
Discussion and Open Problems
Time Complexity Analysis
Theorem
The algorithm of finding equilibrium prices and allocations for
linear utility functions in Fisher’s model needs to run
O(n4
(log n + n log U + log M))
times maximal-flow algorithm.
Since (1 − 1
n2 )n2
∼ 1
e
∼ 1
2
, we can observe that every O(n2
)
phases, |γ(p)|2
is reduced by a factor of half. Hence, the
number of phases is at most
O(n2
lg(∆4
M2
)) = O(n2
(4 lg n + 4n lg U + 2 lg M))
, since M2
/2i
≤ 1/∆4
.
51 / 67

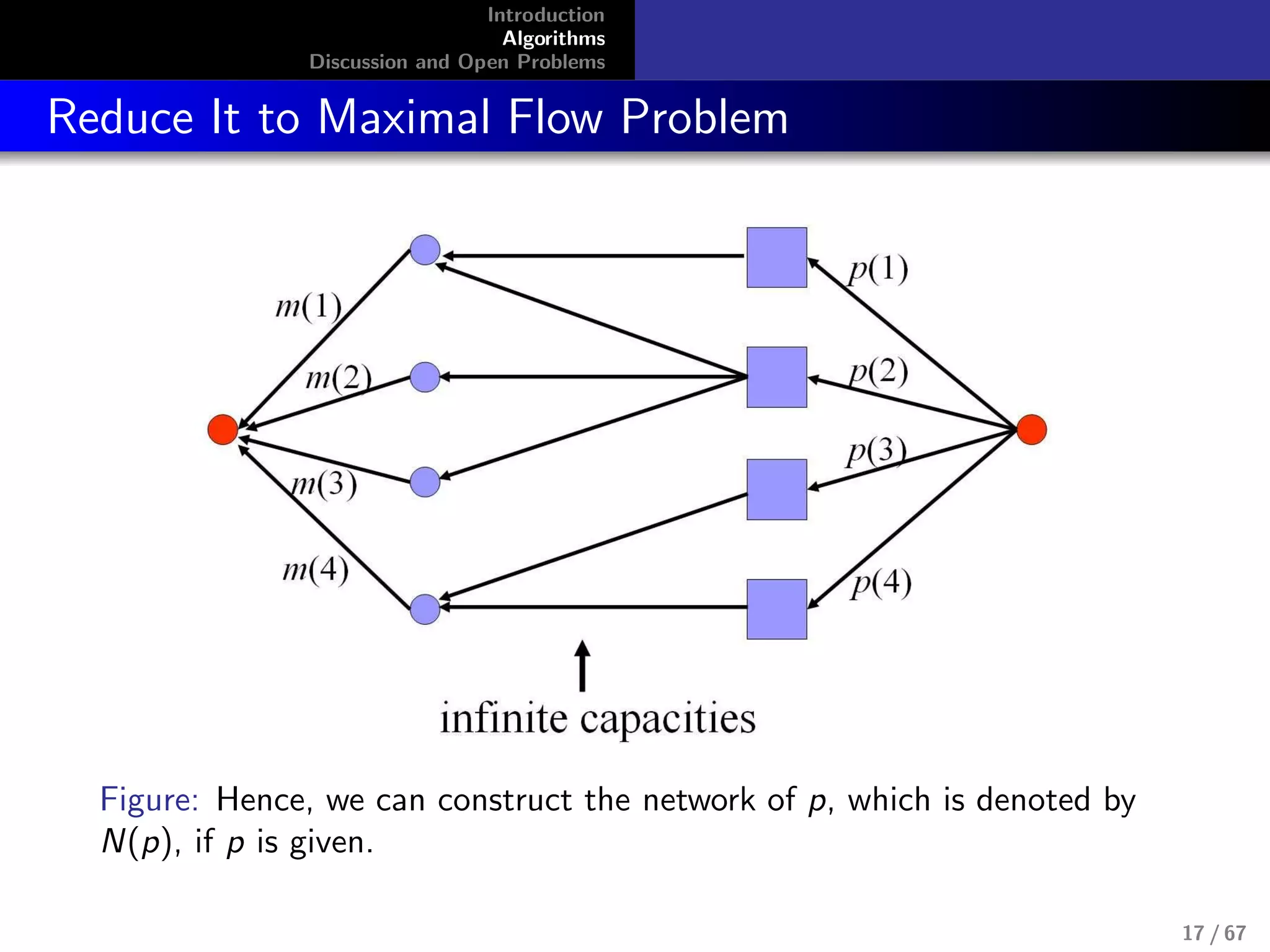
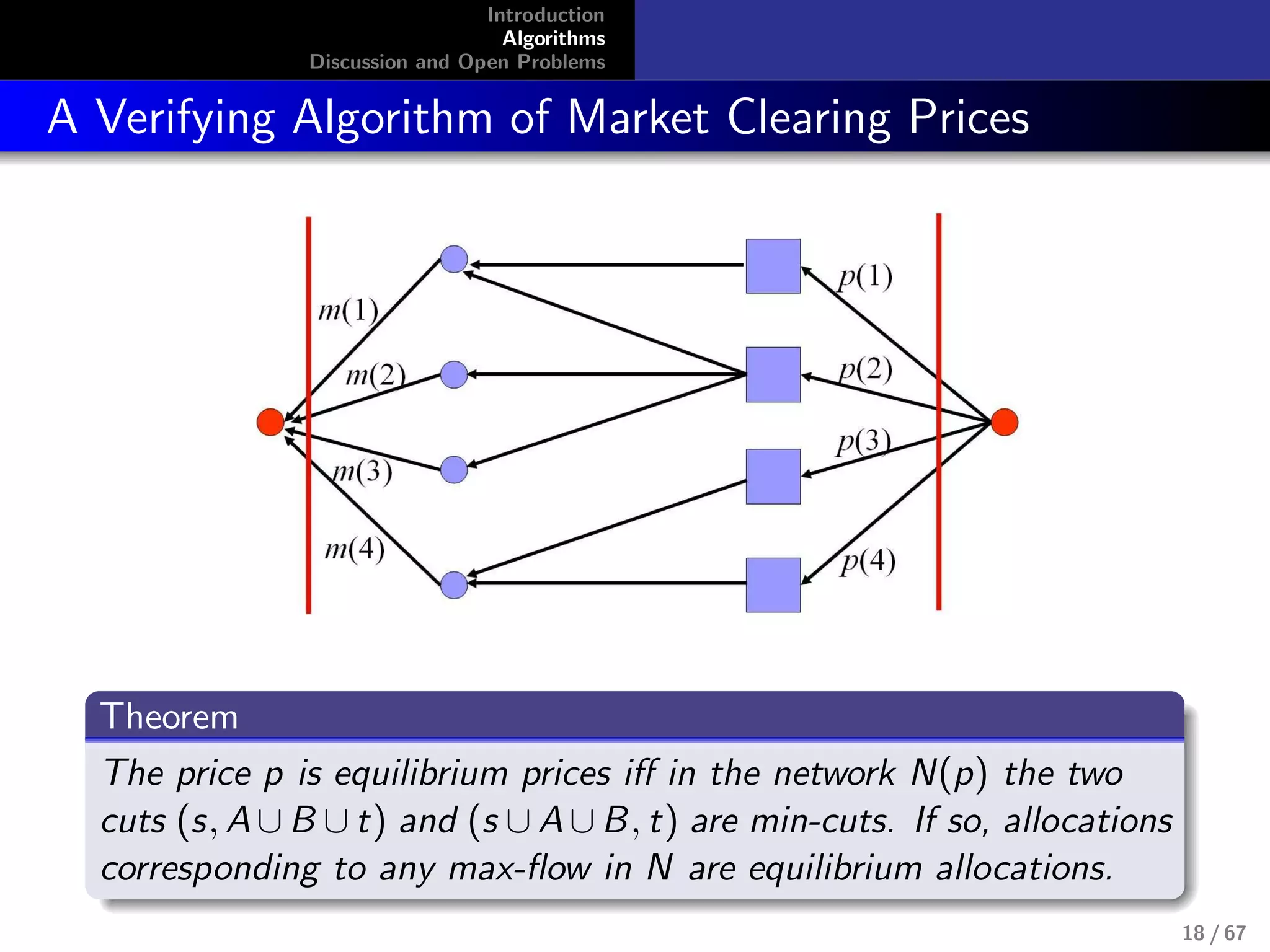
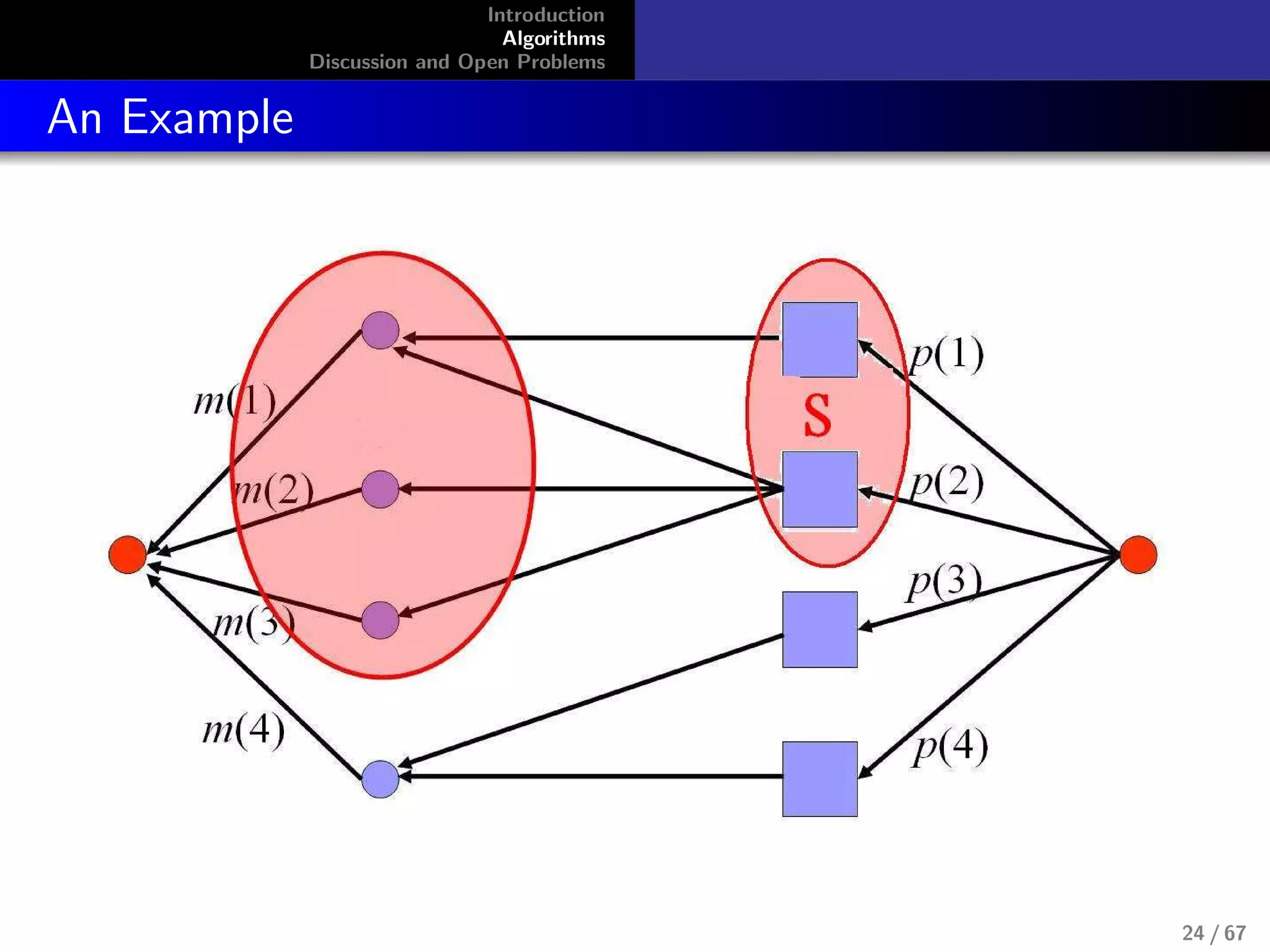
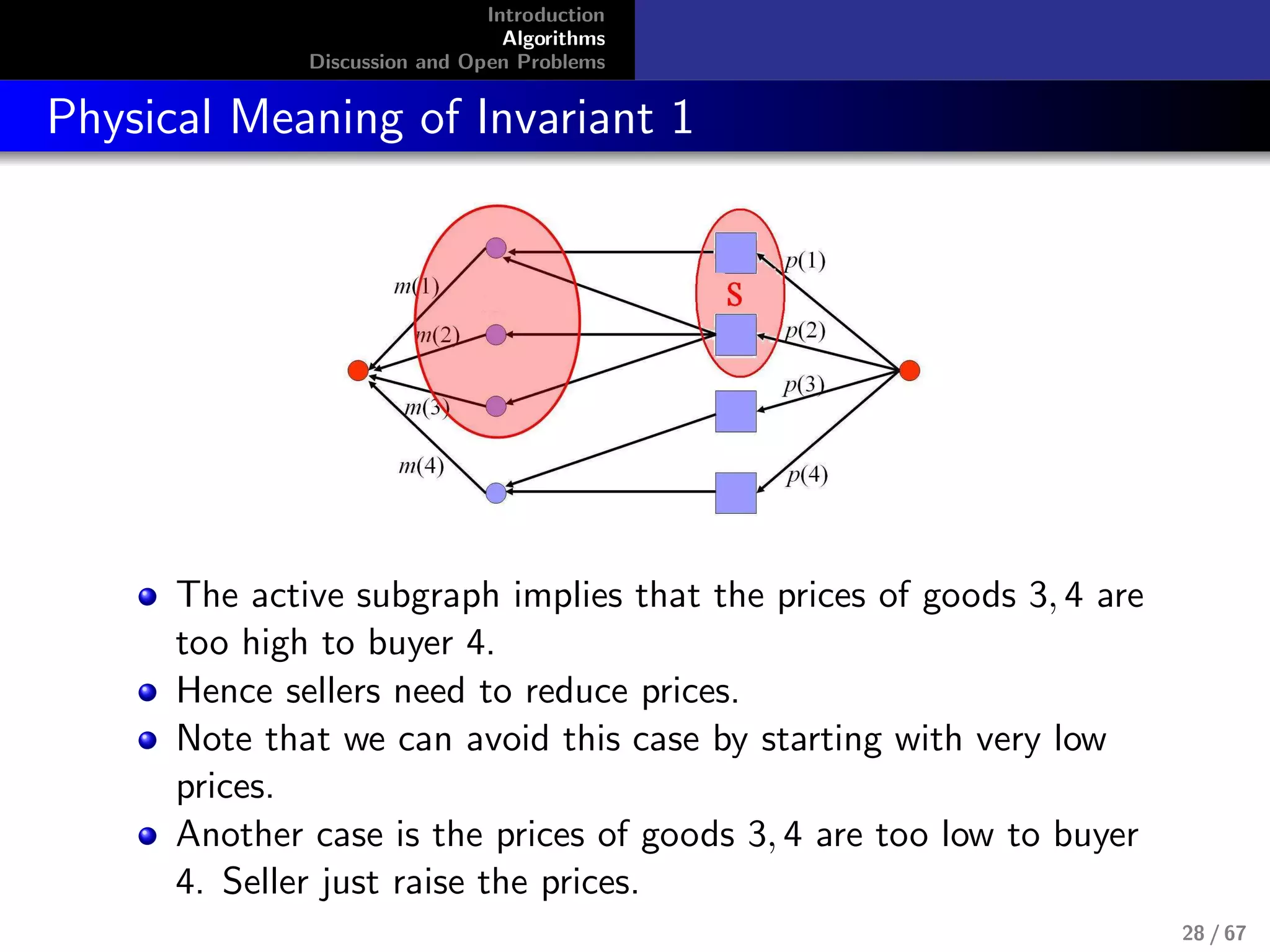
52. Introduction
Algorithms
Discussion and Open Problems
Arrow-Debreu model: An Auction-Based Algorithm
Jain proved that Arrow-Debreu’s Model with Linear Utility
Functions is in P at 2007[4], however it is based on ellipsoid
algorithm. And ellipsoid algorithm is slow in practice.
Garg et al. [3] proposed an auction-based PTAS for the linear
case of the Arrow-Debreu model.
52 / 67

53. Introduction
Algorithms
Discussion and Open Problems
An Auction-Based Algorithm[3]
1 Initializes the price of each good to be unit, computes the
worth of the initial endowment of each agent, and gives this
money to each agent. All goods are initially fully unsold.
2 LOOP UNTIL (the surplus of the traders becomes sufficiently
small, i.e., amin, or all the goods are assigned.)1
2.1 LOOP UNTIL (no agent has surplus money)
2.1.1 Agent i outbid to buy her optimal good j as many as possible,
i.e., at price (1 + )pj .
2.1.2 If agent i has all good j, update the worth of agents with
price (1 + )pj . And Jump to [2].
1
amin means the minimum amount of initial endowments which a agent has.
53 / 67

54. Introduction
Algorithms
Discussion and Open Problems
Analysis of The Auction-Based Algorithm
Theorem
The performance ratio of above algorithm is (1 − )2.
This algorithm is a natural way to achieves equilibrium, i.e., it
always sells an agent her optimal goods relative to current prices p.
Consider the case that agent i doesn’t run out her money. Let M
denote the total worth of i’s initial endowment at terminating
prices. Assume that she spent M1 of this. Since the total surplus
money left at termination is at most amin, M1 ≥ (1 − )M.
54 / 67

55. Introduction
Algorithms
Discussion and Open Problems
Analysis of The Auction-Based Algorithm
On the other hand, agent i runs out her monet.
Some part of good j may have been sold at price (1 + )pj to
agent i, even though the equilibrium price announced is pj . Hence
she didn’t not get the total utilities M, i.e., the total worth of i’s
initial endowment at terminating prices. We assume she spent
money M1. Then we have
Her real utilites =
M1
1 +
≥
(1 − )M
1 +
≥ (1 − )2
M
55 / 67

56. Introduction
Algorithms
Discussion and Open Problems
Analysis of The Auction-Based Algorithm
Theorem
The algorithm given above finds an approximate equilibrium for the
linear case of the Arrow-Debreu model in time
O
mn
2
log
nvmax
aminvmin
log
vmax
vmin
Denote by pmax the maximum price assigned to a good by the
algorithm.
56 / 67

57. Introduction
Algorithms
Discussion and Open Problems
Analysis of The Auction-Based Algorithm
Each iteration raises the price of a good by a factor of (1 + ).
Hence
O(n log1+ pmax)
How many rounds in an iteration? The total surplus at the
beginning of the iteration is npmax, and the algorithm terminates
as soon as the total surplus is at most amin. Hence
O(log1+
npmax
amin
)
57 / 67

58. Introduction
Algorithms
Discussion and Open Problems
Analysis of The Auction-Based Algorithm
O(log1+
npmax
amin
) is an upper bound of the number of rounds in an
iteration, although this case only occurs at the case that this
algorithm terminates at the first iteration.
Note that the ratio of maximum to minimum price of a good is
bounded by umax
umin
, where ui,j means utility per unit money of trader
i for good j. Therefore, Pmax is also bounded by umax
umin
.
Since each round costs O(m), we have the upper bound of the
number of rounds
O (n log1+
umax
umin
) × (log1+
numax
umin
amin
) × m
58 / 67

59. Introduction
Algorithms
Discussion and Open Problems
Discussion and Open Problems
Linear utility functions is too restrictive to be
useful. Concave utility functions are considered
especially useful in economics.
Obtaining a polynomial time algorithm for
Concave utility functions is a premier open
problem today.
Other interesting market problem, e.g., Google
AdWord Market.
Advertisers provide bids for keywords they are
interested in. Maximize total revenue of Google.
59 / 67

60. Introduction
Algorithms
Discussion and Open Problems
References I
Devanur, N. R., Papadimitriou, C. H., Saberi, A., and Vazirani, V. V.
Market equilibrium via a primal-dual-type algorithm.
In FOCS ’02: Proceedings of the 43rd Symposium on Foundations of Computer Science (Washington, DC,
USA, 2002), IEEE Computer Society, pp. 389–395.
Devanur, N. R., Papadimitriou, C. H., Saberi, A., and Vazirani, V. V.
Market equilibrium via a primal–dual algorithm for a convex program.
J. ACM 55, 5 (2008), 1–18.
Garg, R., and Kapoor, S.
Auction algorithms for market equilibrium.
In STOC ’04: Proceedings of the thirty-sixth annual ACM symposium on Theory of computing (New York,
NY, USA, 2004), ACM, pp. 511–518.
Jain, K.
A polynomial time algorithm for computing an arrow–debreu market equilibrium for linear utilities.
SIAM Journal on Computing 37, 1 (2007), 303–318.
Nisan, N., Roughgarden, T., Tardos, E., and Vazirani, V. V.
Algorithmic Game Theory.
Cambridge University Press, New York, NY, USA, 2007.
60 / 67

61. Introduction
Algorithms
Discussion and Open Problems
How to Find the Tight Set
Let p denote the current price vector (i.e. at x = 1).
We first present a lemma that describes how the
min-cut changes in N(xp) as x increases. Define
x∗
= min
S=∅,S⊆A
mf (Γ(S))
mf (S)
the value of x at which a nonempty set goes tight.
Let S∗
denote the tight set at prices x∗
p.
61 / 67

62. Introduction
Algorithms
Discussion and Open Problems
Find the Tight Set
Recall Lemma 1
For given prices p network N(p) satisfies the
Invariant 1 iff.
∀S ⊆ A, mf (S) ≤ mf (Γ(S))
if x ≤ x∗
, then (s, A ∪ B ∪ t) is a min-cut.
if x > x∗
, then (s, A ∪ B ∪ t) is not a min-cut.
If (s ∪ A1 ∪ B1, A2 ∪ B2 ∪ t) is a min-cut in
N(xp) then S∗
⊂ A1.
62 / 67

63. Introduction
Algorithms
Discussion and Open Problems
Find the Tight Set
Figure: Consider x = 2.1 > x∗
= 2. The cut is impossible containing the
edges from goods 3, 4 to buyers 1, 2, 3, since their weights are infinity.
Note that 140 < 147, 126 < 180. Since only 10x + 60x exceeds the
money flow of its neighbors, S∗
⊂ A1.
If we assume x = mf (B)/mf (A) at first, then we can solve it
recursively by above this lemma.
63 / 67

64. Introduction
Algorithms
Discussion and Open Problems
Balanced Flow
Theorem
Computing the balanced flow needs to run at most n times
maximal-flow algorithm.
Sketch of Proof : Let mavg := ( i m(i) − j pj )/|B| . Compute
the maximum flow in the equality subgraph after subtracting mavg
from the capacity of each edge adjacent t. Let (S, T) be the
maximal s-t min-cut in that network. s ∈ S, t ∈ T. If T = {t}
then the current maximum flow is balanced. Otherwise, let N1 and
N2 be the networks induced by T ∪ {s} and S ∪ {t} respectively.
Repeated by divided and conquer approach.
64 / 67

65. Introduction
Algorithms
Discussion and Open Problems
Sketch of Proof of Theorem of Balanced Flow
Figure: Let x = 2. We assume that this graph already substract mavg .
And we get the min-cut. Then we have mavg = (180 − 120)/3 = 20.
Hence we have a new graph N with money (80, 40, 0). Compute the
min-cut for N , we have T = {t} for N , hence it is a balanced flow of
N . 65 / 67

66. Introduction
Algorithms
Discussion and Open Problems
Sketch of Proof of Theorem of Balanced Flow
Claim that the union of balanced flows in N1 and N2
is a balanced flow in N(p).
66 / 67

67. Introduction
Algorithms
Discussion and Open Problems
Sketch of Proof of Theorem of Balanced Flow
Clearly, the number of goods in the biggest piece
drops by at least 1 in each iteration. Therefore, the
depth of recursion is at most n.
Observe that the sub-instance of size 1 doesn’t need
to compute max-flow.
Hence, the total computational overhead is n
max-flow computations.
67 / 67