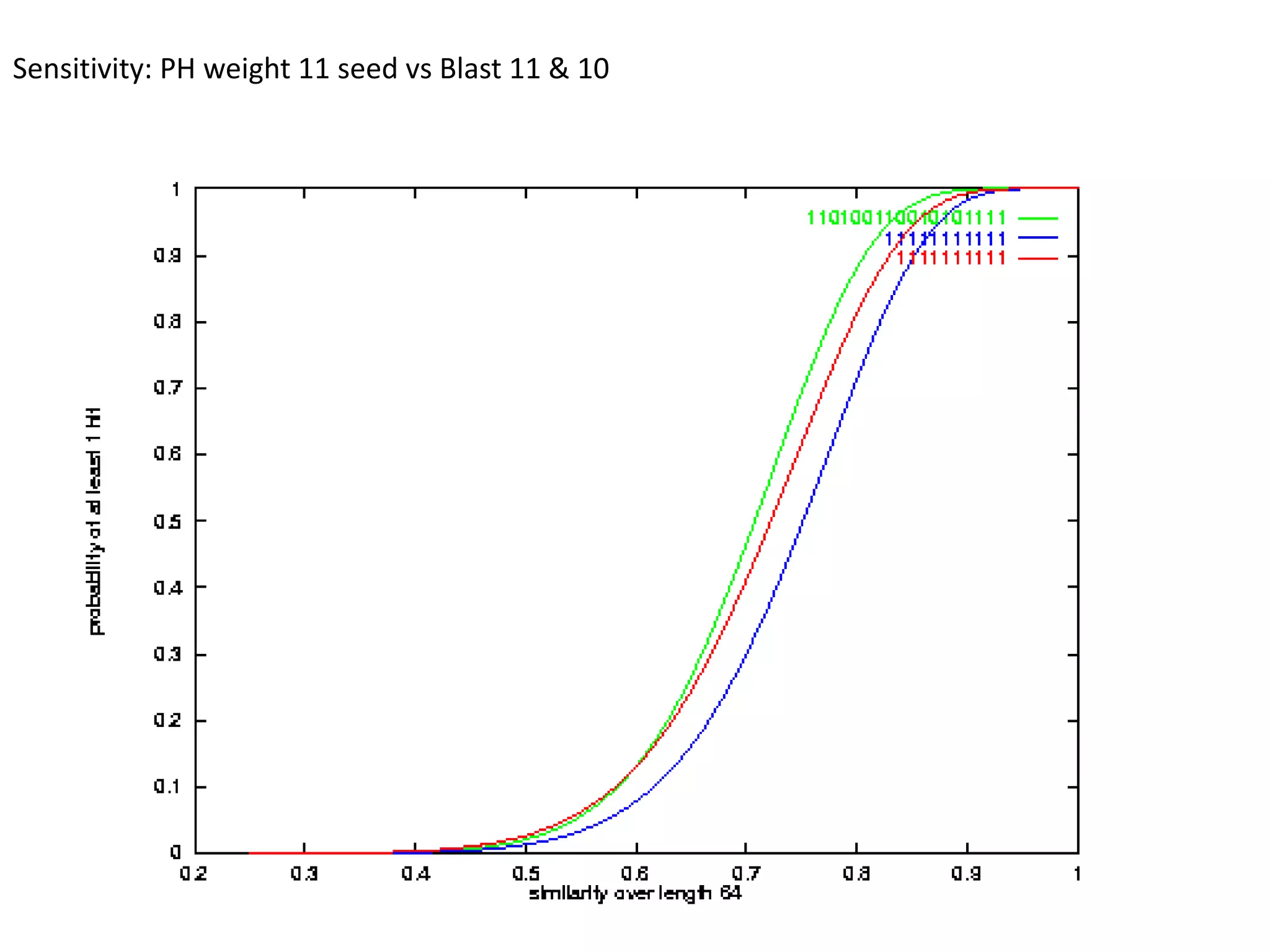
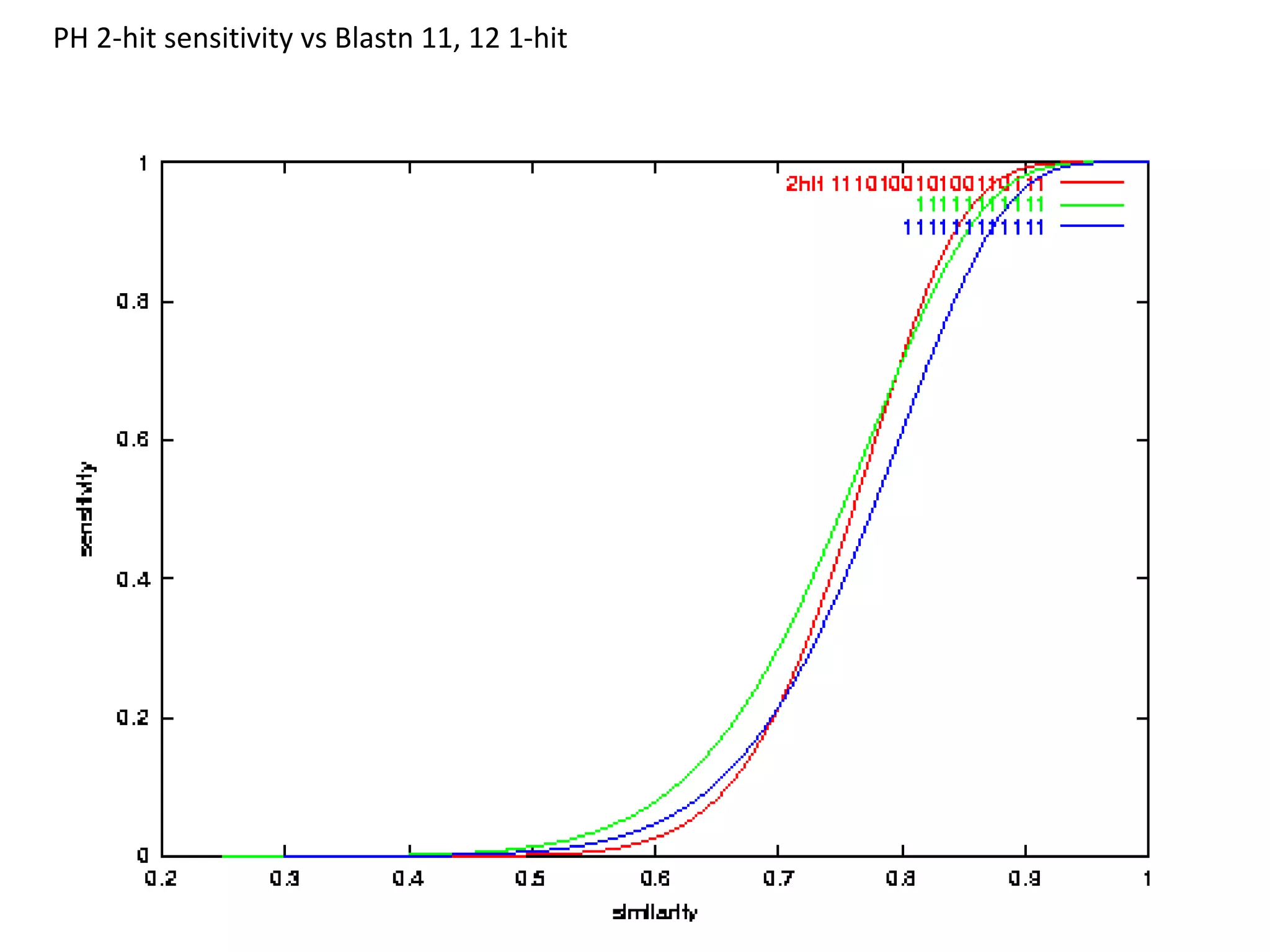
Spaced seeds are used for alignment and pattern matching in bioinformatics. They allow for some positions in the seed to be "don't care" positions represented by an asterisk, unlike BLAST seeds which require matches at every position. This simple change significantly increases the probability of hitting homologous regions while reducing spurious matches. Formally, the expected number of hits of a spaced seed within a region is lower than for a BLAST seed, but the probability of the seed hitting the region is higher, improving sensitivity. Multiple spaced seeds and hidden Markov models have also been used to improve alignment.

1. Alignment: Spaced Seed
2012-03-16
LEAST Seminar
Abner Huang
< abnercyh@cs.nthu.edu.tw >
CSBB Lab, NTHU

2. Outline
• Introduction
• Theory
• Remarks
2

3. Stringology
• String matching
• Pattern matching
• Periodicities
• Data structure
• Text Compression
• Alignment
3

4. Alignment
• Spelling correction
• Bitext word alignment
• File comparison (diff)
• Amino acid sequences comparison
4

5. Nature Milestones in DNA: BLAST
Altschul, S. F., Gish, W., Miller, W., Myers, E. W. & Lipman, D. J. Basic local
alignment search tool. J. Mol. Biol. 215, 403–410 (1990) 5

6. A. Califano and I. Rigoutsos, “Flash: A fast look-up algorithm for string homology,”
in Proceedings of the 1st International Conference on Intelligent Systems for
Molecular Biology (ISMB), pp. 56-64, July 1993.
6

7. Spaced seed
Spaced seed, Multiple spaced seeds,
Vector (Relaxed) seed, Neighbor seeds
7

8. Outline
• Introduction
• Theory
• Remarks
8

9. Optimal Spaced Seed
(Ma, Tromp, Li: Bioinformatics, 18:3, 2002, 440-445)
• Spaced Seed: nonconsecutive matches and
optimized match positions.
• Represent BLAST seed by 11111111111
• Spaced seed: 111*1**1*1**11*111
– 1 means a required match
– * means “don’t care” position
• This seemingly simple change makes a huge
difference: significantly increases hit prob. to
homologous region while reducing bad hits.

10. Formalization
• Given i.i.d. sequence (homology region) with
Pr(1)=p and Pr(0)=1-p for each bit:
1100111011101101011101101011111011101
• Which seed is more likely to hit this region:
– BLAST seed: 11111111111
– Spaced seed: 111*1**1*1**11*111
111*1**1*1**11*111

11. Sensitivity: PH weight 11 seed vs Blast 11 & 10

12. PH 2-hit sensitivity vs Blastn 11, 12 1-hit

13. Expect Less, Get More
• Lemma: The expected number of hits of a weight W length M
seed model within a length L region with similarity p is
(L-M+1)pW
Proof: The expected number of hits is the sum, over the L-M+1 possible
positions of fitting the seed within the region, of the probability of W
specific matches, the latter being pW. ■
• Example: In a region of length 64 with 0.7 similarity, PH has
probability of 0.466 to hit vs Blast 0.3, 50% increase. On the
other hand, by above lemma, Blast expects 1.07 hits, while PH
0.93, 14% less.

14. Why Is Spaced Seed Better?
A wrong, but intuitive, proof: seed s, interval I, similarity p
E(#hits) = Pr(s hits) E(#hits | s hits)
Thus:
Pr(s hits) = Lpw / E(#hits | s hits)
For optimized spaced seed, E(#hits | s hits)
111*1**1*1**11*111 Non overlap Prob
111*1**1*1**11*111 6 p6
111*1**1*1**11*111 6 p6
111*1**1*1**11*111 6 p6
111*1**1*1**11*111 7 p7
…..
• For spaced seed: the divisor is 1+p6+p6+p6+p7+ …
• For BLAST seed: the divisor is bigger: 1+ p + p2 + p3 + …

15. Improvements
• Brejova-Brown-Vinar (HMM) and Buhler-
Keich-Sun (Markov): The input sequence can
be modeled by a (hidden) Markov process,
instead of iid.
• Multiple seeds
• Brejova-Brown-Vinar: Vector seeds
• Csuros: Variable length seeds – e.g. shorter
seeds for rare query words.

16. Outline
• Introduction
• Theory
• Remarks
16

17. Thank You