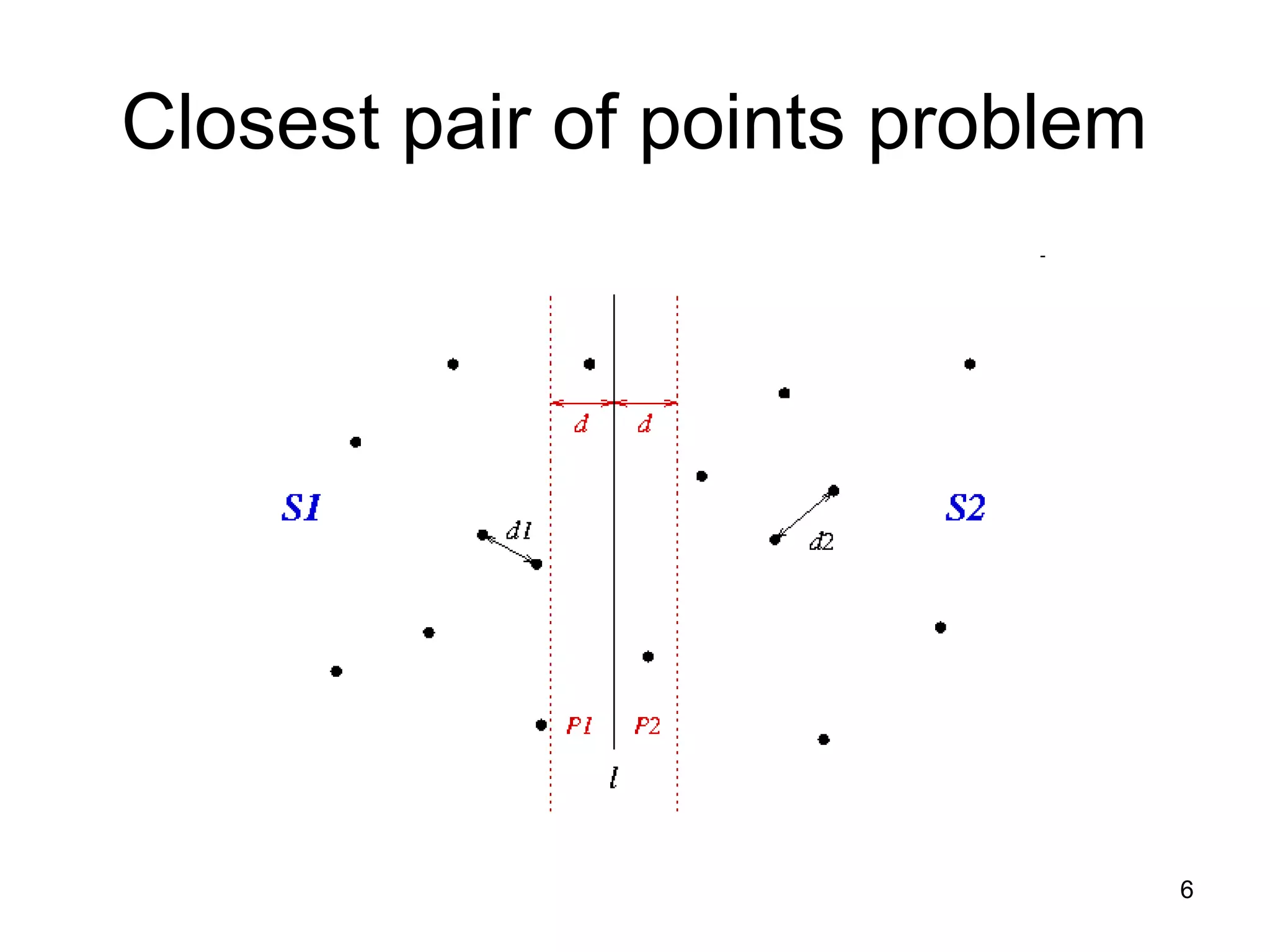
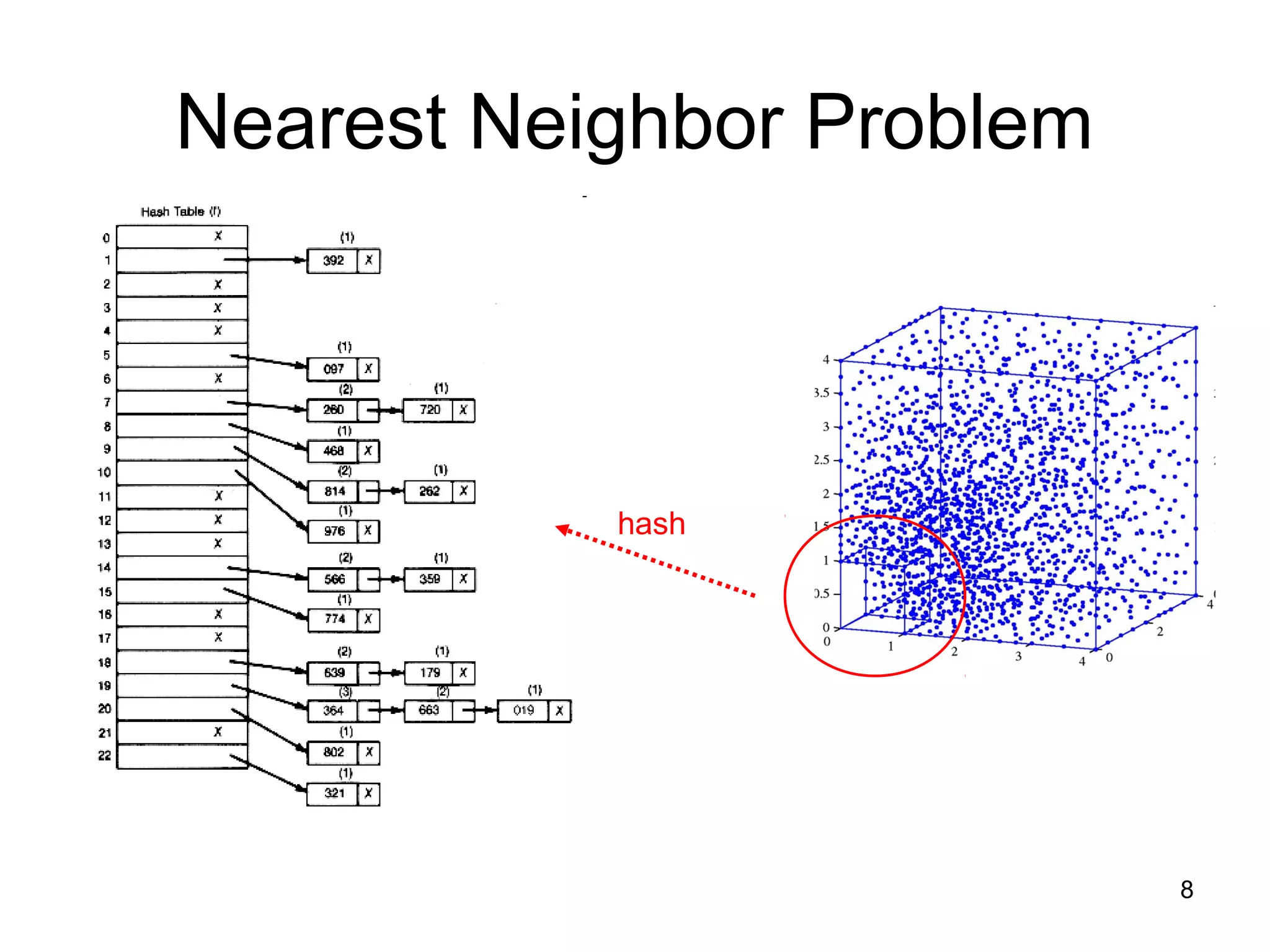
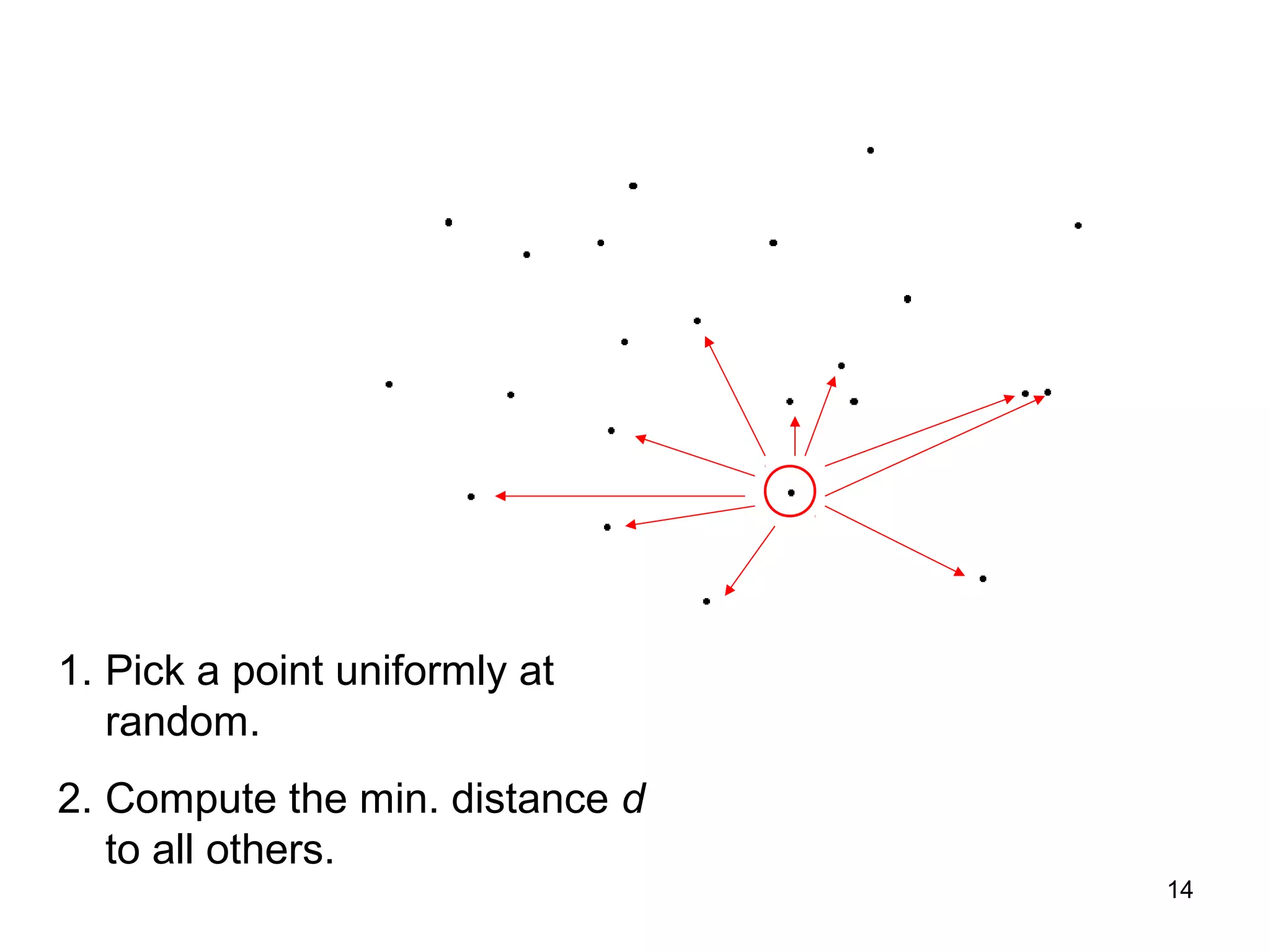
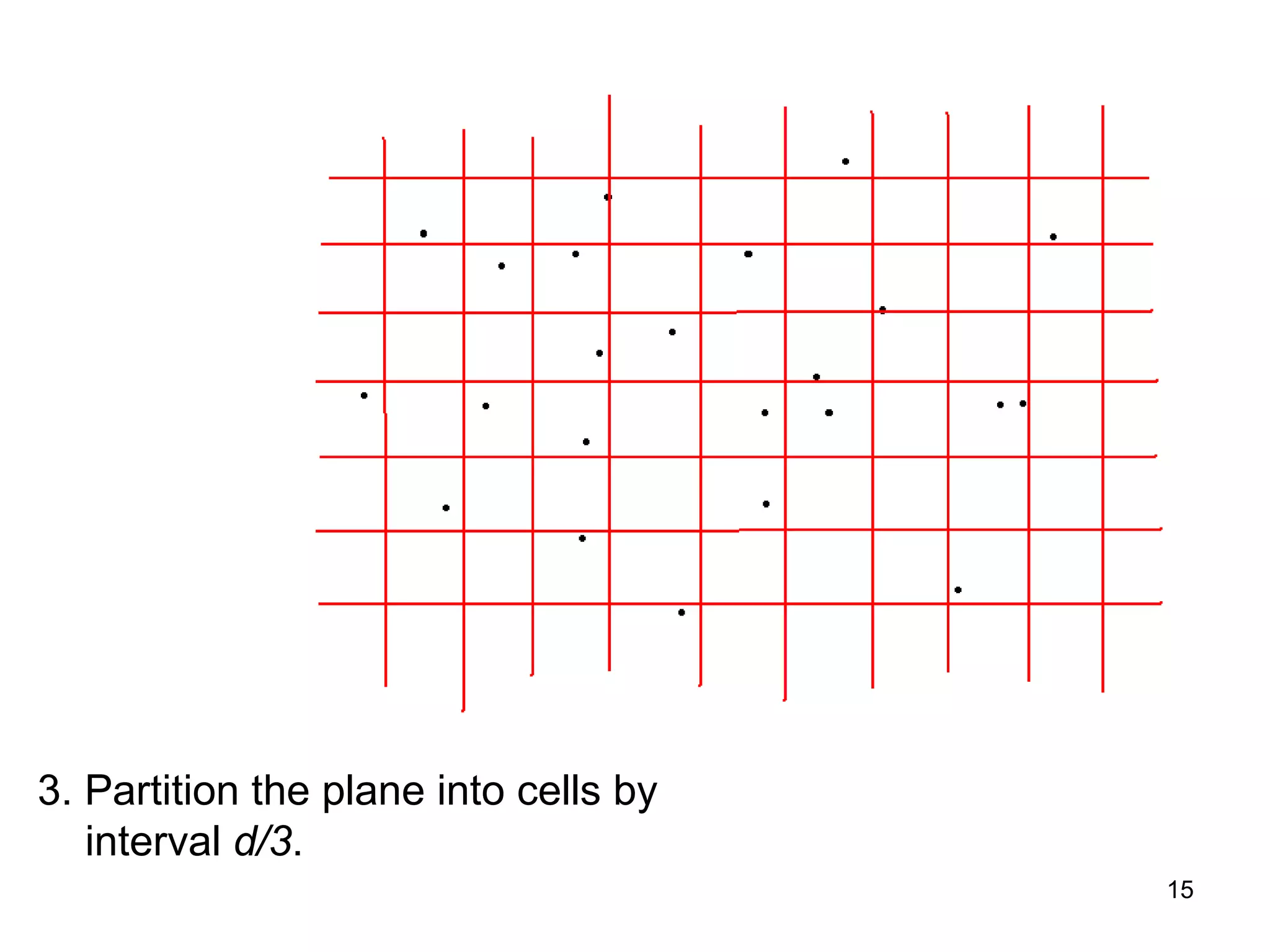
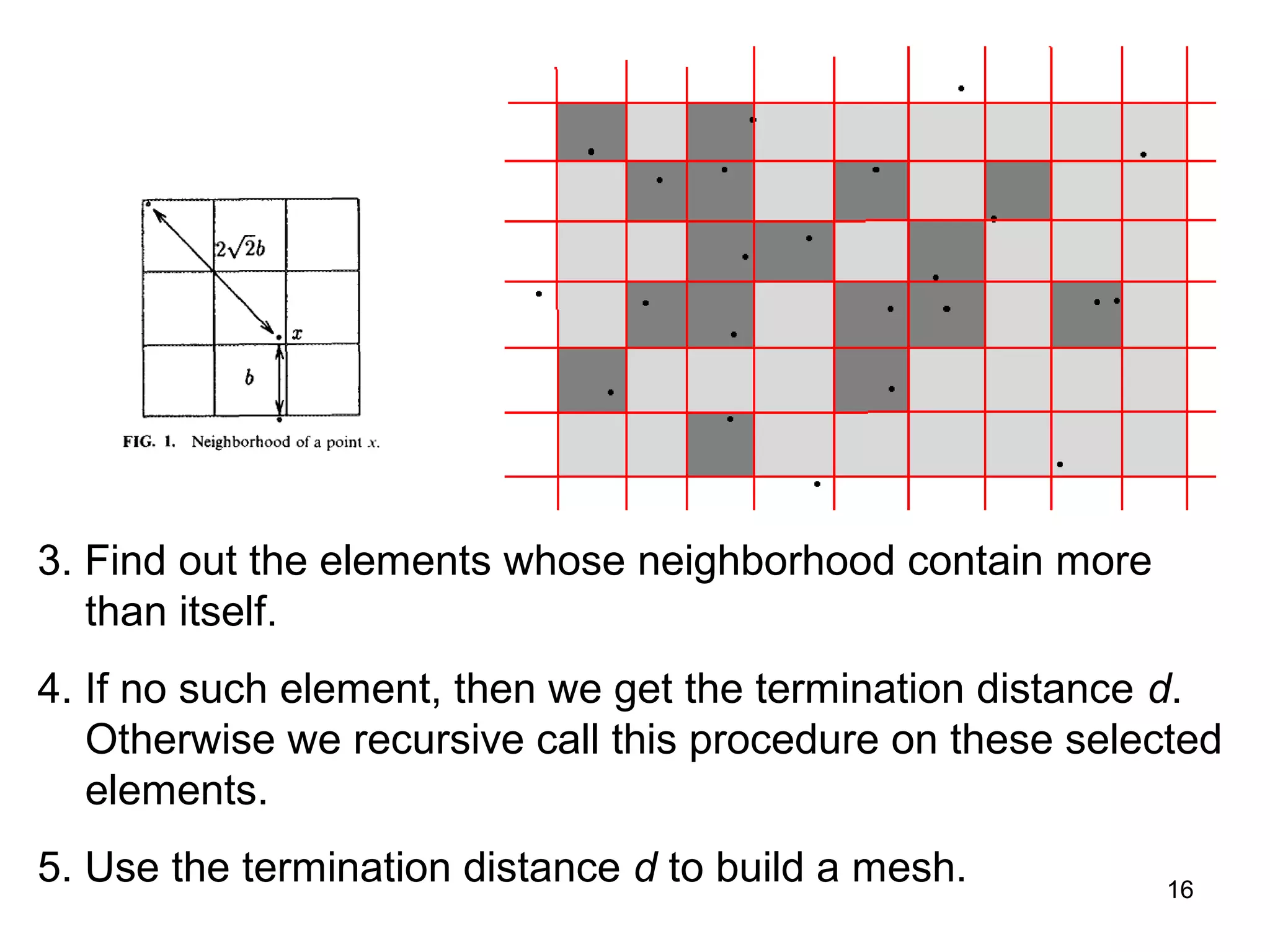
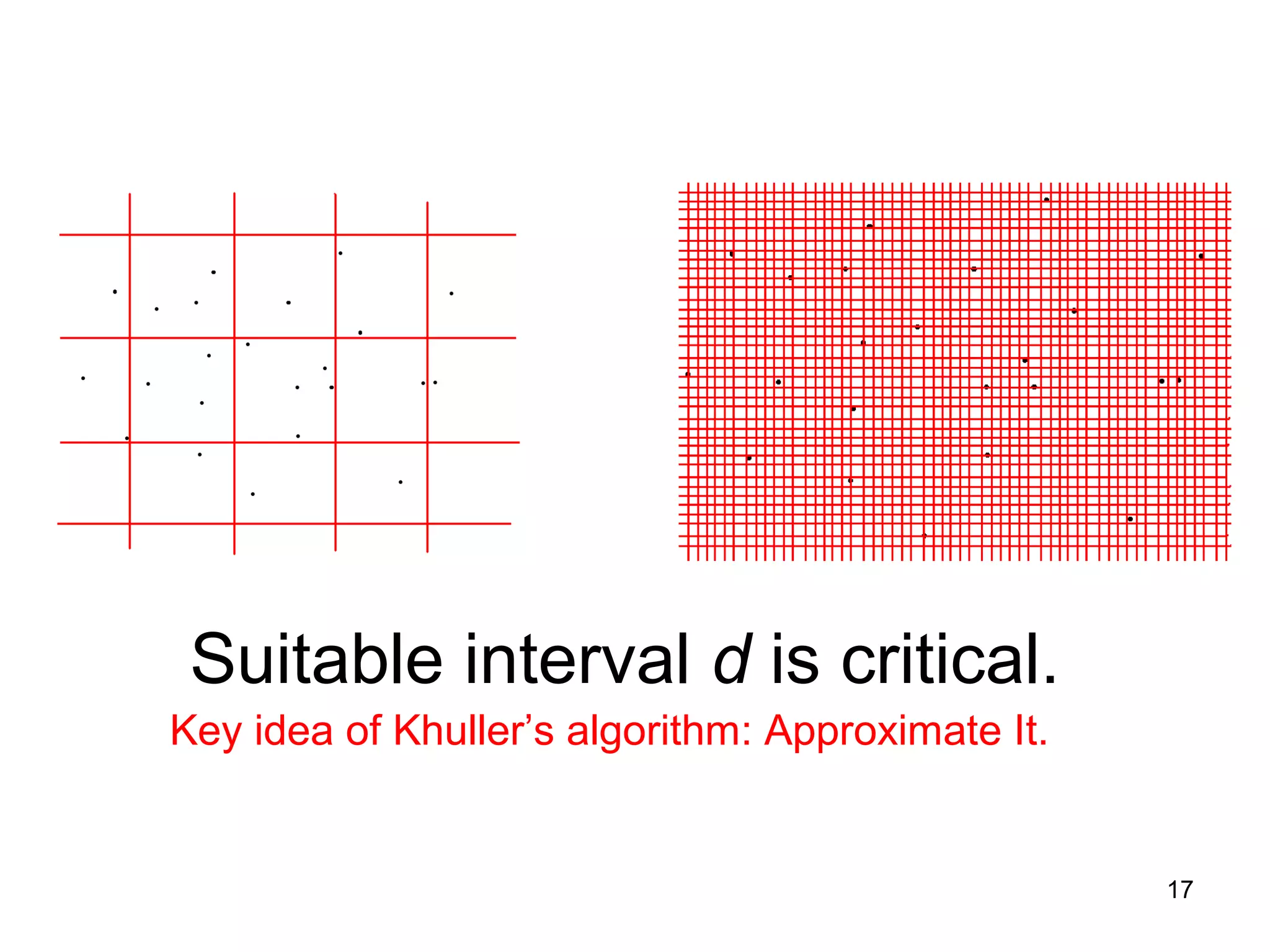
The document discusses randomized algorithms for solving the closest pair of points problem, beginning with Rabin's randomized linear time algorithm from 1976. It describes how Khuller and Matias later proposed a simpler randomized sieve algorithm in 1995. It also discusses how Fortune and Hopcroft showed in 1979 that Rabin's algorithm relies on the power of randomness to break lower bounds, presenting a deterministic O(n log log n) time algorithm. The document raises questions about the assumptions of unit-cost operations like hashing and floor functions.

1. 1
A Small Debate of Power of
Randomness
Abner Huang
2009-10-16

2. 2
Power of Randomness
M. O. Rabin
The citation for the Turing Award,
awarded in 1976 jointly to Rabin and
Dana Scott for a paper written in 1959,
[1] states that the award was granted:
For their joint paper "Finite Automata
and Their Decision Problem," which
introduced the idea of nondeterministic
machines, which has proved to be an
enormously valuable concept. Their
(Scott & Rabin) classic paper has been
a continuous source of inspiration for
subsequent work in this field

3. 3
Power of Randomness
• Quick Sort: O(n lg n)
– Worst case : O(n^2)
• Randomized Quick Sort
– Expected : O(n lg n)
• C. A. R. Hoare + M. Blum
– Quick Sort + Median : Worst-case O(n lg n)
• Is randomness really helpful?

4. 4
P = BPP?

5. 5
The Story Was Originated at
……..

6. 6
Closest pair of points problem

7. 7
Closest pair of points problem
• Classical Result is O(n lg n) by divide-and-
conquer.
• Rabin proposed an expected linear time Las
Vegas randomized algorithm.
– Rabin, M. O., Traub, J. .F. (ed.) Probabilistic algorithms In Algorithms
and Complexity, New Directions and Recent Trends, Academic Press,
1976, 21-39

8. 8
Nearest Neighbor Problem
hash

9. 9
An Example
Let’s sample s
points from
the data set.
And compute
the minimum
distance d
among those
s points.

10. 10
An Example (cont.)
Using the
distance d, we
will partition
the plane into
cells.
Thus each cell
has few points

11. 11
An Example (cont.)
• If we are lucky, the adjacent cells of each
cell will contain few points. Hence we can
check it one by one.

12. 12
However, Rabin’s proof is
complicated!

13. 13
A Simpler Version
• Ref.: Khuller, S. & Matias, Y.
A simple randomized sieve
algorithm for the closest-pair
problem, Information and
Computation, 1995, 118, 34-
37

14. 14
1. Pick a point uniformly at
random.
2. Compute the min. distance d
to all others.

15. 15
3. Partition the plane into cells by
interval d/3.

16. 16
3. Find out the elements whose neighborhood contain more
than itself.
4. If no such element, then we get the termination distance d.
Otherwise we recursive call this procedure on these selected
elements.
5. Use the termination distance d to build a mesh.

17. 17
Suitable interval d is critical.
Key idea of Khuller’s algorithm: Approximate It.

18. 18
Four Facts

19. 19
Proof
Lemma

20. 20

21. 21
Deterministic Algorithm
• Ref.: Fortune, S. & Hopcroft, J. E.
A note on Rabin’s nearest-
neighbor algorithm Information
Processing Letters, 1979, 8, 20-23
• How powerful the
randomness in Rabin’s
algorithm is?
– It breaks the lower
bound!!! John E. Hopcroft
Turing Award in 1986

22. 22
Key idea: re-hash S if
there is one bucket
which has more than
sqrt(n) elements.

23. 23
An Example
Order of
input
sequence

24. 24
An element might
appear in recursive
calls at both two
lines, e.g.,
Note that : the input sequence is
not sorted
B1 B2 B3

25. 25
An Example of Worse Case
Order of
input
sequence

26. 26
• This case occurs when points fall into the
same bucket but are processed by
different levels of line 5-9, where a level is
defined by one iteration of the loop (line 5-
9).
• For a call, since there at most sqrt(n)
levels, there are at most sqrt(n) points in a
bucket at line 19.

27. 27
Its (ideal) recursive partition
Each partition have no more than
sqrt(n) elements.
If all sub-problems are disjoint, then it is easy to
show that this algorithm is in O(n lg (lg n))

28. 28
PROOF
• In a level, after calling FINDINT to
process a non-empty bucket B with b
elements, we will increase (b-1) non-
empty sets after the call.
Let’s also
define it
a level.

29. 29
• If we apply this idea to recursive calls at a
level and all levels, then we have
where k is the number of calls, and bi is
the size of input elements of the i-th call.
• The total cost involved those recursive
calls is bounded by
where d is a big constant.

30. 30
• Since the slop of x log(log x) is strictly
increasing, we have the following property
for r s>2.≧
• It means to get the upper bound, more
large bi are better.

31. 31

32. 32

33. 33
Discuss
• Rabin’s assumption:
– Random number is available.
– Square-Root is constant time operation.

34. 34
Discuss
• Rabin’s assumption:
– Random number is available.
– Square-Root is constant time operation.
– Hashing function, i.e., floor is a constant
time operation.
• It is important! In Rabin’s original paper, it
only achieves O(n lg n) without hashing
method.
• In Hopcroft’s paper, it costs O(n lglg n)
deterministically.

35. 35
Q: Is Unit-Cost Floor Function
Reasonable?
• Recall The Sorting Algorithm.
–Well known lower bound: O(n lg n)
–What does it mean?

36. 36
Q: Is Unit-Cost Floor Function
Reasonable?
• Recall The Sorting Algorithm.
–Well known lower bound: O(n lg n)
–What does it mean?
–We can sort n numbers by c*n lg n
computation steps?

37. 37
Q: Is Unit-Cost Floor Function
Reasonable?
• Recall The Sorting Algorithm.
– Well known lower bound: O(n lg n)
– What does it mean?
– We can sort n numbers by c*n lg n
computation steps?
– Is it reasonable, if the numbers are in the
interval from 2^{n} to 2^{2^{2^{n}}}?

38. 38
Q: Is Unit-Cost Floor Function
Reasonable?
• Recall The Sorting Algorithm.
– Well known lower bound: O(n lg n)
– What does it mean?
– We can sort n numbers by c*n lg n
comparisons.

39. 39
Even x+y, x-y,
xy, x/y are not
in constant
time.

40. 40
Unit-Cost Assumptions
Moore's Law

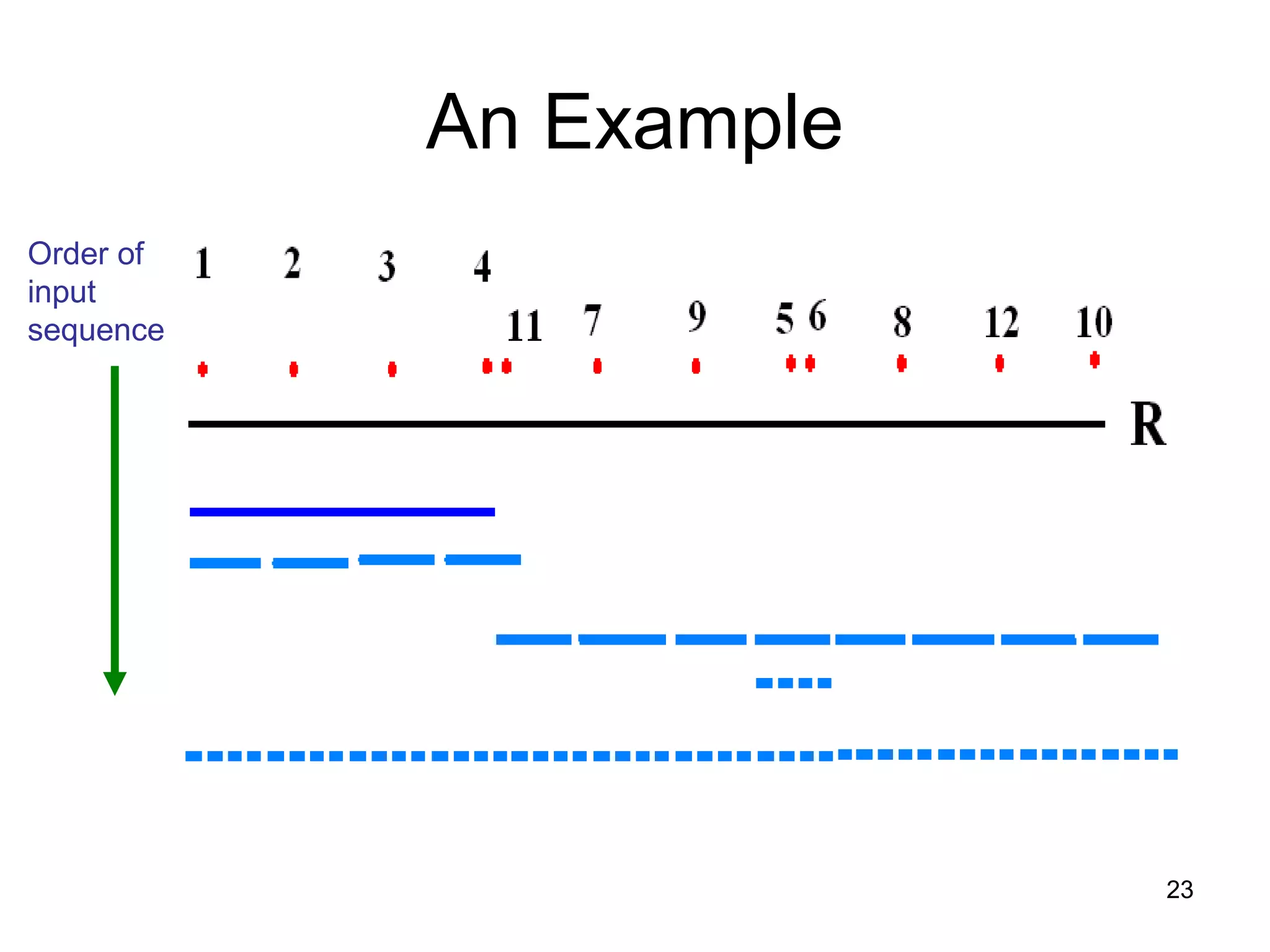
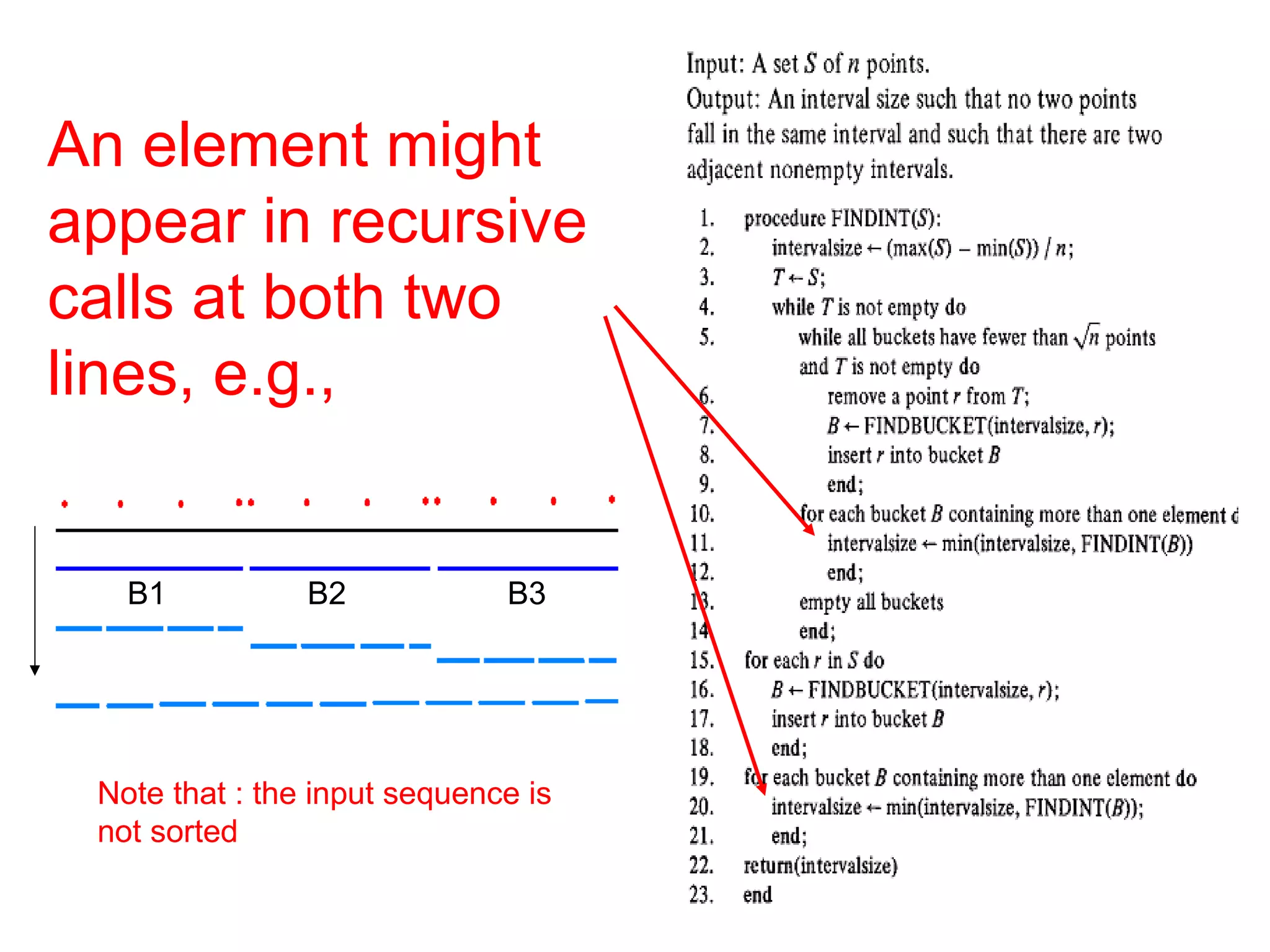
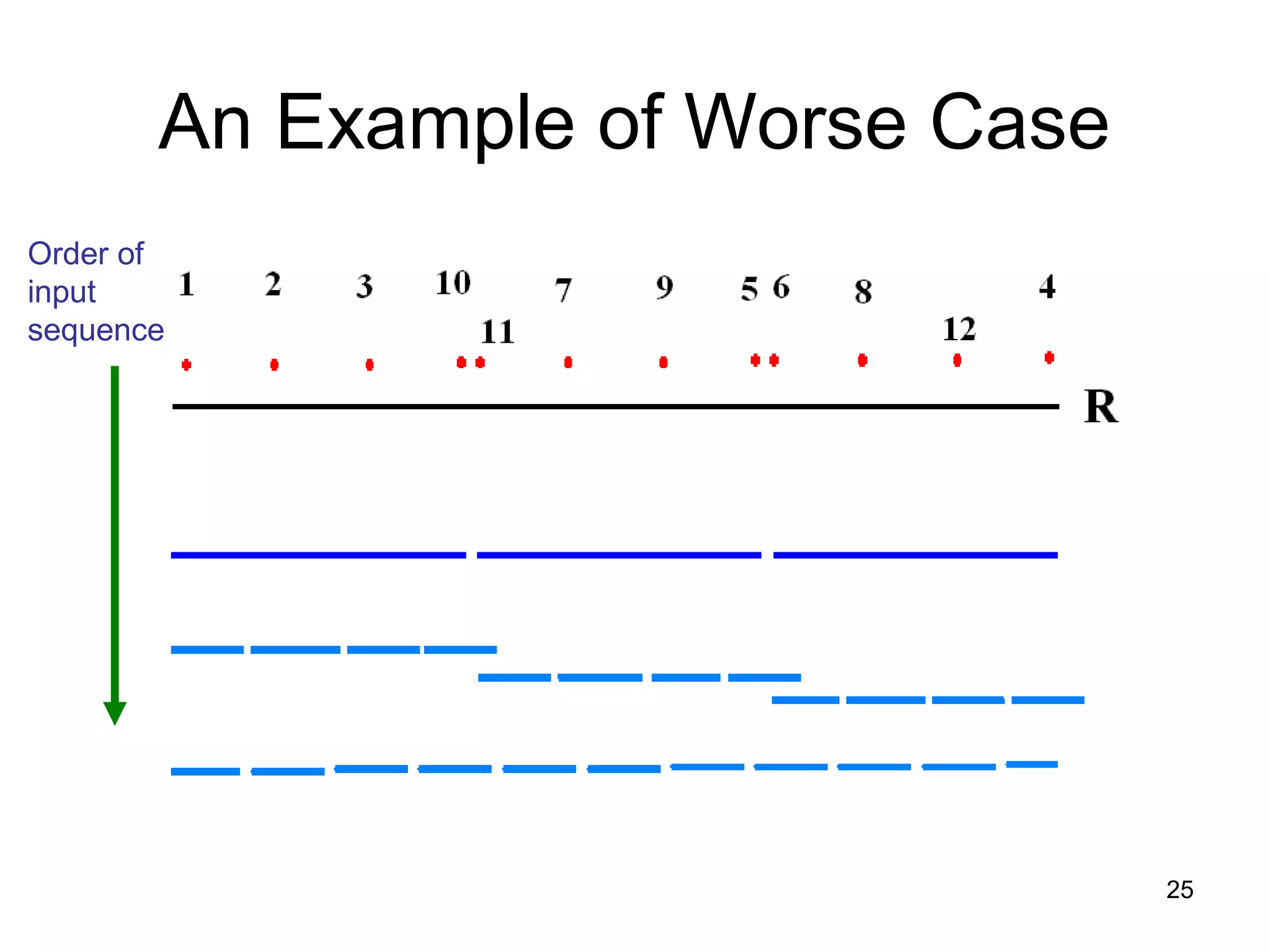
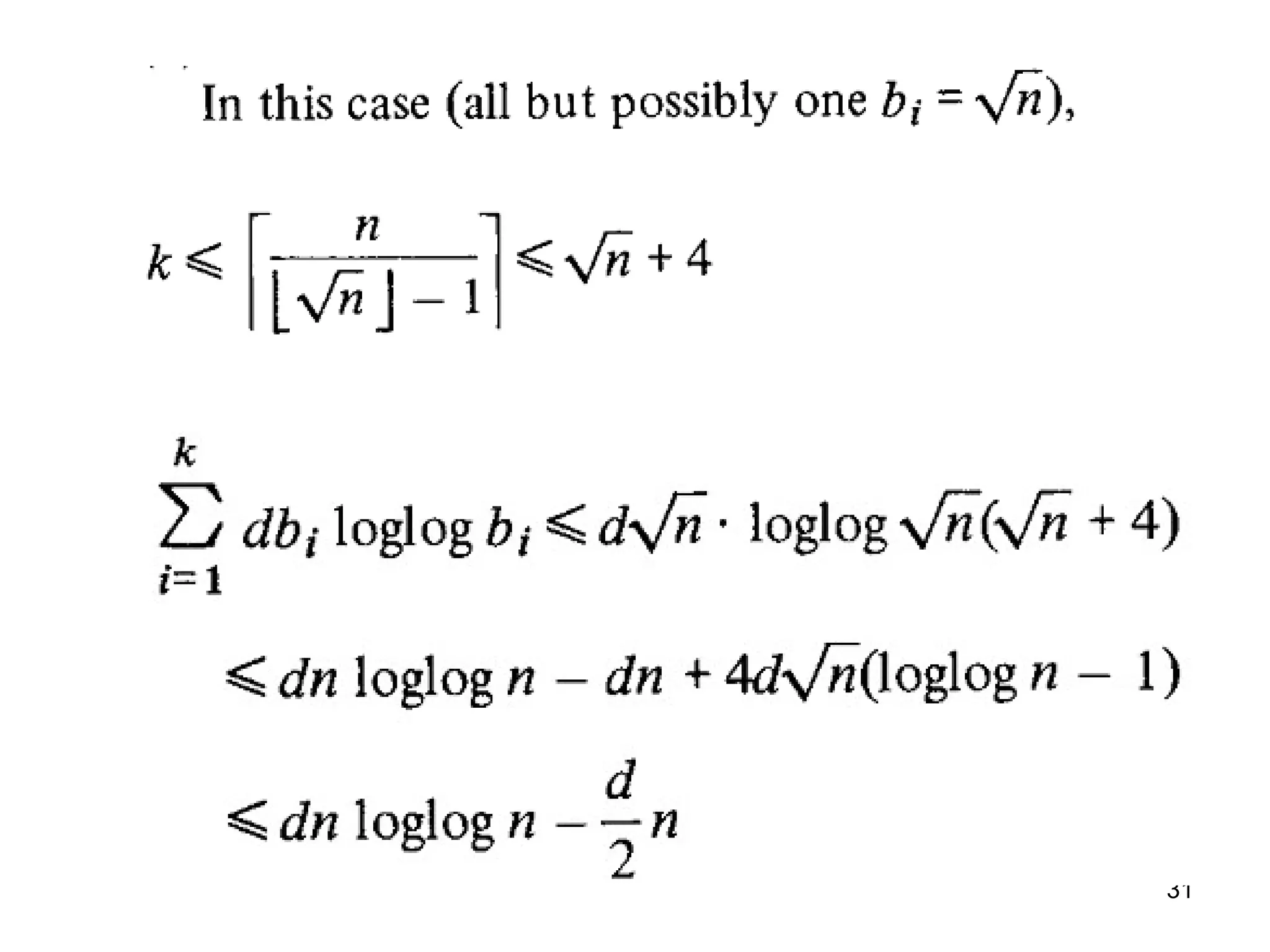
41. 41
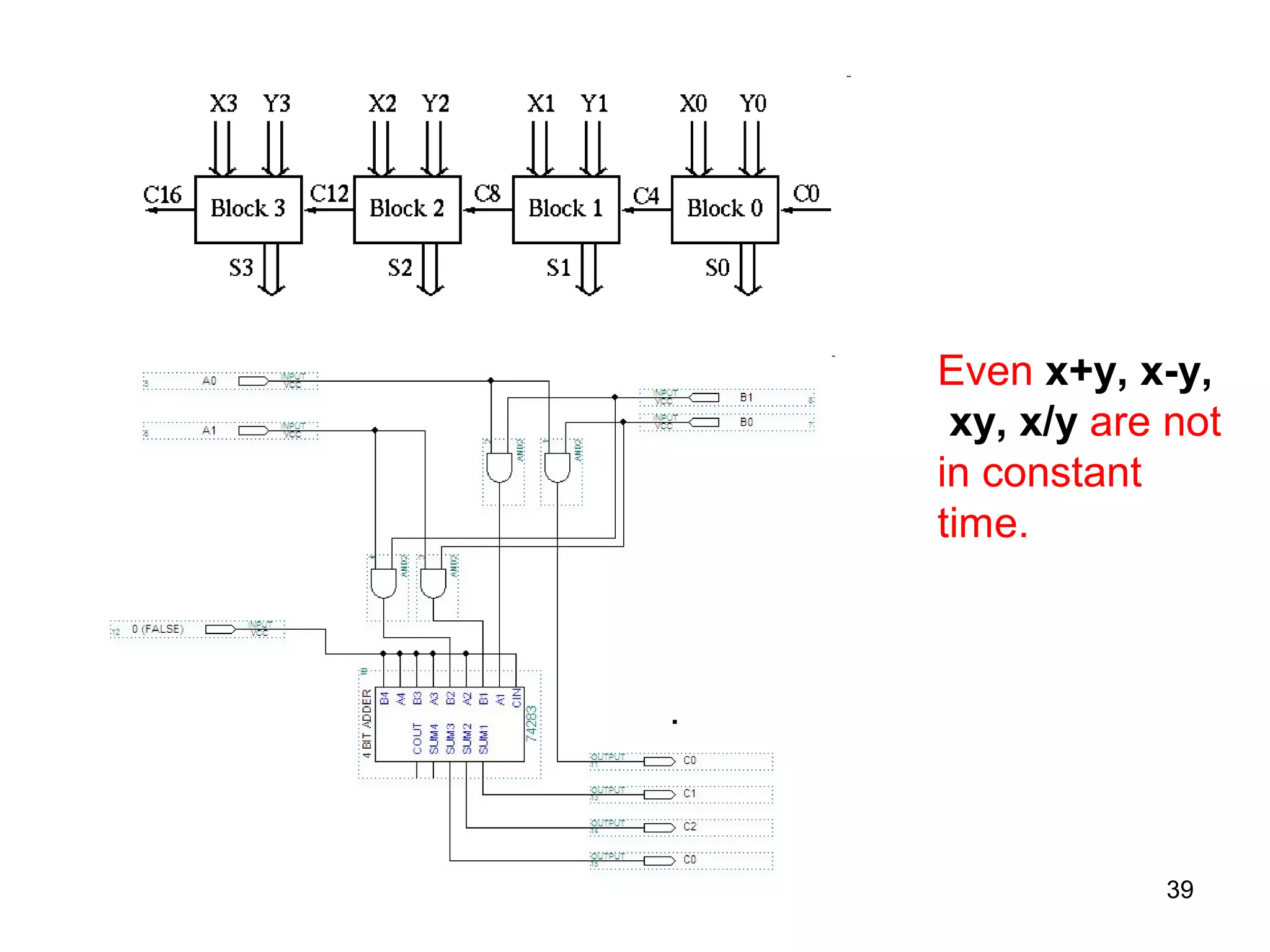
Q: Is Unit-Cost Floor Function
Reasonable in Theory?
• Rabin's randomized algorithm for closest
pairs [1976].
• Schönhage 1979: If we could compute
x+y, x-y, xy, x/y, x
for any real x,y in a single step, then we
could solve NP- and even PSPACE-
complete problems in polynomial time

42. 42
Furthermore
• A few years later, Bertoni et al. [bms-scram-
85] generalized the same approach to the
#P-complete problem #SAT: How
many satisfying assignments does this
Boolean formula have?
• Peter van Emde Boas has a great
discussion of "the unreasonable power of
integer
multiplication" in his survey of models of
computation [e-mms-90].

43. 43

44. 44
We now have a
deterministic O (n lg lg n)
algorithm and an
expected O(n) algorithm.

45. 45
We now have a
deterministic O (n lg n) algorithm
and an
expected O(n) algorithm.
Happy Ending?

46. 46
Curse of Dimensionality!!!

47. 47
A Simple Calculus
• Given: 1 million points in 100-
dimension space.
– Clever algorithm
– 2100
~1030
– 1030
x ( 106
lg 106
)
– Brute-force method
– 106
x 106

48. 48
High Dimensional
Geometry
How to beat the brute-force method?
Indyk, Piotr.; Motwani, Rajeev. (1998). ", Approximate Nearest
Neighbors: Towards Removing the Curse of Dimensionality.".
Proceedings of 30th Symposium on Theory of Computing.

49. 49
It is another story.

50. 50
THANKS FOR YOUR
ATTENTION

51. 51
Ref.
• Rabin, M. O., Traub, J. .F. (ed.) Probabilistic algorithms
In Algorithms and Complexity, New Directions and
Recent Trends, Academic Press, 1976, 21-39
• Khuller, S. & Matias, Y. A simple randomized sieve
algorithm for the closest-pair problem, Information and
Computation, 1995, 118, 34-37
• Fortune, S. & Hopcroft, J. E. A note on Rabin’s nearest-
neighbor algorithm Information Processing Letters, 1979,
8, 20-23

52. 52
Ref.
• Schönhage, A. On the power of random access
machines Automata, Languages and Programming:
Sixth Colloquium, Graz, Austria, July 16–20, 1979, 1979,
71, 520-529
• Bertoni, A.; Mauri, G. & Sabadini, N. Ausiello, G. &
Lucertini, M. (ed.) Simulations Among Classes of
Random Access Machines and Equivalence Among
Numbers Succinctly Represented Analysis and Design
of Algorithms for Combinatorial Problems, North-Holland,
1985, 109, 65 - 89
• van Emde Boas, P. van Leeuwen, J. (ed.) Machine
models and simulation Handbook of Theoretical
Computer Science, Elsevier, 1990, A, 1-66