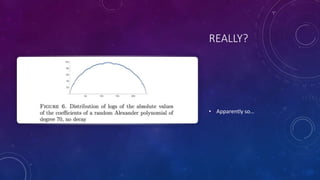
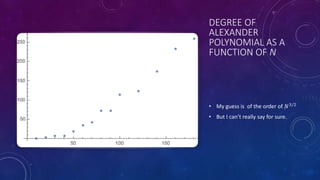
Random knots can be modeled by taking random Fourier series or connecting random points on the unit sphere. For the Fourier model, the limiting curve is continuously differentiable if the Fourier coefficients decay quickly enough. The expected number of self-intersections is also finite in this case. For both models, the Alexander polynomial coefficients appear to concentrate on the unit circle, unlike polynomials with random coefficients. Different random knot models may produce different topological and geometric properties worth further study. Computation of invariants like the Alexander polynomial remains challenging for models with many segments.

1. RANDOM KNOTS
IGOR RIVIN, UNIVERSITY OF ST ANDREWS AND TEMPLE UNIVERSITY

2. WHY RANDOM TOPOLOGY?
• We know what (for example) the average life expectancy of a random human (or random American, or
random Frenchman born in 1797) is. We also know the standard deviation of this quantity, so we can
say that if someone lives until the age of 120, they are very unusual, which can be interpreted in a
number of ways (if we are an insurance company, we probably don’t have to worry too much about
someone living to 120, on the other hand, if we are a doctor, we might want to study the 120 year old,
to see what about him (or, more commonly, her) is different.
• So, it’s both easier than understanding every single person, and informative, in that it gives us an
overview of the situation.
• Plus, the randomness lets us generate large examples, and defeat the “law of small numbers”.

3. EASY IS GOOD

4. WHAT DOES ”RANDOM” MEAN?
GOOD THING ABOUT HUMANS IS THAT THERE ARE ONLY FINITELY MANY OF THEM. SADLY, NOT
SO FOR MOST MATHEMATICAL STRUCTURES.

5. WHAT IS A RANDOM KNOT?

6. What is a random knot?
First question is, what is a knot?

7. WHAT IS A KNOT?
• A knot is a simple closed curve in 𝑅3
• A simple closed curve in 𝑅3 is a map from 𝑆1 to 𝑅3.
• A map from 𝑆1
to 𝑅3
. Is a triple of map from 𝑆1
to R.
• A map from 𝑆1 to R is a periodic function.
• Which is given by a Fourier series: 𝑓 𝜃 = 𝑘=0
∞
𝑎 𝑘 sin 2𝑘𝜋𝜃 + 𝑏 𝑘 cos 2𝑘𝜋𝜃
• So, a knot is a triple of Fourier series, and a random knot is a triple of random Fourier series!

8. HISTORICAL NOTE
• As far as I know, this model was introduced by Bill Thurston in the early 1980s.
• He wanted to know the distribution of knot types, and was proposing to use the (then) new Jones
polynomial to study it.
• He had a graduate student (Bruce Ramsay) working on it, but nothing came of this.

9. RANDOM TRIGONOMETRIC SERIES
• We want to keep things simple, so we assume that the coefficients (the 𝑎 𝑘 and the 𝑏 𝑘) are random
variables. For simplicity, we assume they are independent, Gaussian, but not necessarily identical – we
can make the variance a function of k.
• We can also assume that they are identical, but there are only N frequencies (so, a Fourier polynomial
of degree N).

10. HOW MANY DIFFERENT KNOT TYPES DO WE GET?
• How do we tell them apart?
• By simplifying the question: we look at the knot projection onto some plane (for our Fourier knots, the
first two coordinates form a nice plane).
• Instead of knot types (which are hard to tell apart), we look at the number of self-intersections of the
projection – this upper-bounds the crossing number of the knot.
• And now?

11. CROSSING NUMBER OF A KNOT
• The crossing number is the minimal number of self-intersections of any topologically equivalent knot
onto a plane (we can assume that the plane is always the xy plane, by rotating the knot).
• Known to be in NP (Hass, Lagarias, Pippenger) and co-NP (Lackenby), not known to be polynomial time.

12. RANDOM PLANE CURVES
• What does decay of coefficients translate into?

13. PLANE CURVE, QUADRATIC DECAY

14. PLANE CURVE, 𝑘−3/2
DECAY

15. PLANE CURVE, LINEAR DECAY (SHOULD LOOK
FAMILIAR)

16. PLANE CURVE, 𝑘−1/2
DECAY (NOT REALLY)

17. MAIN OBSERVATIONS:
• The limiting curve is continuously differentiable (almost surely) if the decay is 𝑘−(
3
2
+𝜖)
for some positive
𝜖.
• The expected number of self intersections is finite under precisely the same conditions.

18. HOW DO YOU PROVE THE LATTER?

19. FOR US, THE FUNCTION IS
• (F(s)-F(t))/(s-t).

20. COROLLARY
• The probability that a random smooth curve has more than N crossings decays at least like 1/N.
• NOT the truth: the truth is that the decay is at least exponential in N – not clear how to prove yet
(concentration of measure?)

21. FACT
• There are exponentially many (in N) knots with at most N crossings, so if we order knots by crossing
number, we will get a (cumbersome) statement.

22. BUT WHAT DO THESE KNOTS “LOOK LIKE”
• Problem: hard to compute interesting invariants.
• Except one: the Alexander polynomial (defining which will take us too far afield, but can be defined as a
graph determinant with a variable thrown in). This can be computed in polynomial time for polygonal
curves (not fast polynomial time).

23. COEFFICIENT DISTRIBUTION OF ALEXANDER
POLYNOMIALS OF RANDOM KNOTS
• For this, we want crazy knots sooner, so we use the second model (trigonometric polynomials of degree
N with identical independent coefficients.

24. COEFFICIENT DISTRIBUTION, REVEALED

25. REALLY?
• Apparently so…

26. WHAT DO THE
ZEROS LOOK LIKE?
• Notice the zero-free region

27. NOTHING LIKE
RANDOM RECIPROCAL
POLYNOMIALS
• Notice concentration of zeros on the
unit circle

28. HOW MODEL-SPECIFIC IS THIS?
• Let’s try another model
• Think of a knot as a (closed) path.
• Now, take a sample of the uniform distribution on the unit sphere, and connect point 1 to point 2, point
2, to point 3, …, point N to point 1. (almost surely non-self-intersecting).

29. HISTORICAL NOTE
• This is a variant of a model due to Ken Millett – he proposed taking a sample of the uniform distribution
in the unit cube.
• The exact model I am looking at was the subject of a question of Joseph O’Rourke on MathOverflow
(the question was: what was the crossing number of a random such knot obtained by taking N points on
the unit sphere. The obvious guess is Ω(𝑁2), but it was conjectured by Bill Thurston (again) that the
hyperbolic volume grows as 𝑁3/2
, and he suggested looking at the Alexander polynomial degree as an
estimator of the number of crossings.

30. DEGREE OF
ALEXANDER
POLYNOMIAL AS A
FUNCTION OF N
• My guess is of the order of 𝑁3/2
• But I can’t really say for sure.

31. WHAT DO WE GET FOR COEFFICIENTS OF ALEXANDER
POLYNOMIALS?

32. UNIVERSALITY?

33. WHAT OTHER MODELS ARE THERE?
• Take a random 4-regular planar graph, an Euler cycle, and make every vertex an over- or under-
crossing, randomly.
• Take a random walk on 𝑍3
, and when you get a closed loop, see what the knot type is.
• Petal diagrams (given through random permutations)
• Random braids (random words in the braid group)
• Etc

34. WHICH MODEL IS PHYSICALLY/BIOLOGICALLY
APPROPRIATE?
• Study what we see in nature, and then, try to see which model matches.

35. WHAT INVARIANTS TO STUDY?
• Crossing number
• Hyperbolic volume
• Conformal energy
• Coefficients/zeros of other knot polynomials

36. COMPUTATIONAL CAVEATS
• The Fourier model is not so easy to compute with. Why?
• We need a polygonal curve for Alexander polynomial computation
• (we simplify it using Reidemeister moves, but still)
• The complexity is bad (𝑁5
or so) in the number of segments.
• So, we need a sophisticated subdivision algorithm (better than Mathematica’s)
• Not sure what the best method is.
• Second model is very easy, by contrast, but seems less natural.