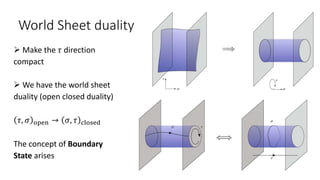
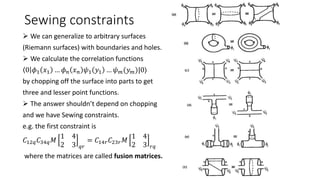
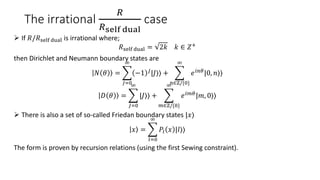
The document discusses conformal field theory (CFT) and its applications, notably in quantum field theory and condensed matter physics. It covers the properties of primary fields, boundary states, and operator product expansions, while also introducing concepts like Virasoro algebra and free bosons. Additionally, it examines boundary conditions and duality in string theory, raising questions about boundary states and their interpretations.

1. Conformal Boundary States
for free boson
Hassaan Saleem

2. What is Quantum Field Theory (QFT)?
 A quantum theory with local operators (fields) 𝜙(𝑥) as degrees of freedom.
 Relativistic QFT is symmetric in spacetime translations, rotations and boosts.
Rotational symmetry + Boost symmetry → Lorentz symmetry
Translation symmetry + Lorentz symmetry → Poincare symmetry
 Should have at least one vacuum (lowest energy state)
 Can have internal (non spacetime) symmetries
 Has a vacuum state |0⟩. Main objects of study are correlation functions
⟨0 𝜙1 𝑥1 … 𝜙𝑛 𝑥𝑛 0⟩

3. Why study Conformal Field Theory (CFT)?
 CFTs can be made very rigorous.
 Fixed Points in RG flow.
 Extensive use in condensed matter physics (phase transitions and
behaviour near criticality).
 Super String Theory is a (super) conformal theory.

4. What is CFT?
 Relativistic QFT + Additional spacetime symmetries (Conformal
Transformations -or CT- in total)
 Defining equation
𝑔𝛼𝛽(𝑥) → Ω2 𝑥 𝑔𝛼𝛽(𝑥)
 These transformations preserve angles
 For 𝐷 = 1, every transformation is conformal
 For 𝐷 > 2, Poincare + Scale Transformation + Special Conformal
𝑥𝜇′
= 𝜆𝑥𝜇
(Scale Transformation)
𝑥𝜇′
𝑥′2
=
𝑥𝜇
𝑥2
− 𝑏𝜇 Special Conformal 𝑥𝜇 →
𝑥𝜇
𝑥2
inversion

5. Conformal
Transformations
for 𝐷 > 2

6. Primary Fields
 A field 𝜙(𝑥) is primary if for 𝒙 → 𝒙′, the field transforms as;
𝜙′
𝒙′
→
𝜕𝒙′
𝜕𝒙
−
Δ
𝐷
𝜙(𝒙)
e.g. for dilations 𝒙 → 𝒙′ = 𝜆𝒙
𝜙′
𝒙′
→ 𝜆−
Δ
𝐷𝜙(𝒙)
 𝜆 is called the scaling dimension of the field.

7. 𝐷 = 2 case (two dimensional CFT)
 Coordinates are (𝑥0, 𝑥1) or (𝑧, 𝑧) where;
𝑧 = 𝑥0
+ 𝑖𝑥1
, 𝑧 = 𝑥0
− 𝑖𝑥1
 CTs are
𝑧 → 𝑓 𝑧 holomorphic transformation
𝑧 → 𝑓 𝑧 (anti − holomorphic transformation)
 Infinitesimal form
𝑧 → 𝑧 + 𝜖 𝑧 = 𝑧 +
𝑛∈ℤ
𝜖𝑛 −𝑧𝑛+1
= 1 +
𝑛∈ℤ
𝜖𝑛 −𝑧𝑛+1
𝜕𝑧 𝑧 = 1 +
𝑛∈ℤ
𝜖𝑛𝑙𝑛 𝑧
𝑧 → 𝑧 + 𝜖 𝑧 = 𝑧 +
𝑛∈ℤ
𝜖𝑛 −𝑧𝑛+1
= 1 +
𝑛∈ℤ
𝜖𝑛 −𝑧𝑛+1
𝜕𝑧 𝑧 = 1 +
𝑛∈ℤ
𝜖𝑛𝑙𝑛 𝑧

8. Virasoro Algebra and Stress tensor
 𝑙𝑛 and 𝑙𝑛 satisfy (Witt algebra)
𝑙𝑛, 𝑙𝑚 = 𝑛 − 𝑚 𝑙𝑛+𝑚
𝑙𝑛, 𝑙𝑚 = 𝑛 − 𝑚 𝑙𝑛+𝑚
𝑙𝑛, 𝑙𝑚 = 0
 Witt algebra can be ‘extended’ to Virasoro algebra
𝐿𝑛, 𝐿𝑚 = 𝑛 − 𝑚 𝐿𝑛+𝑚 +
𝑐
12
𝑚3
− 𝑚 𝛿𝑛+𝑚
Stress tensor (𝑇𝜇𝜈) is defined as
𝑇𝜇𝜈 =
𝛿ℒ
𝛿𝑔𝜇𝜈
⇒ 𝑇𝜇
𝜇
= 0, 𝜕𝜇
𝑇𝜇𝜈 = 0
 𝑇𝑧𝑧 = 𝑇 𝑧 , 𝑇𝑧𝑧 = 𝑇 𝑧 , 𝑇𝑧𝑧 = 𝑇𝑧𝑧 = 0

9. Primary field in 𝐷 = 2 CFT
 In (𝑧, 𝑧) coordinates, a primary field transforms as;
𝜙′ 𝑓 𝑧 , 𝑓 𝑧 =
𝜕𝑓 𝑧
𝜕𝑧
−ℎ
𝜕𝑓 𝑧
𝜕𝑧
−ℎ
𝜙(𝑧, 𝑧)
(ℎ, ℎ) are conformal weights of 𝜙(𝑧, 𝑧).
 Δ = ℎ + ℎ.
 𝑙−1, 𝑙0, 𝑙1 and 𝑙−1, 𝑙0, 𝑙1 correspond to translations, rotations,
dilations and special conformal tr. (globally defined CTs).
 A field is quasi-primary if it follows primary transformation law
only for global CTs.
 𝑇(𝑧) and 𝑇(𝑧) are quasi primary (ℎ = 2, ℎ = 0)

10. Mode expansions
 For a primary field, we have the following mode expansion on (𝑧, 𝑧)
coordinates;
𝜙 𝑧, 𝑧 =
𝑛,𝑚
𝑧−𝑛−ℎ𝑧−𝑚−ℎ𝜙𝑛,𝑚
 For chiral primary fields, we have;
𝜙 𝑧 =
𝑛
𝑧−𝑛−ℎ𝜙𝑛 𝜙 𝑧 =
𝑚
𝑧−𝑚−ℎ𝜙𝑚
e.g. 𝑇 𝑧 and 𝑇 𝑧 , the mode expansions are;
𝑇 𝑧 =
𝑛
𝑧−𝑛−2
𝐿𝑛 𝑇 𝑧 =
𝑚
𝑧−𝑚−2
𝐿𝑚

11. Operator Product Expansion (OPE)
 OPE of two quasi primary operators 𝜙1(𝑧, 𝑧) and 𝜙2(𝑤, 𝑤) is
𝜙1 𝑧, 𝑧 𝜙2 𝑤, 𝑤 =
𝑘
𝐶12𝑘𝑎𝑖𝑗𝑘
𝑛
𝑧 − 𝑤 𝑓(ℎ1,ℎ2,ℎ𝑘,ℎ1,ℎ2,ℎ𝑘,𝑘)
𝜕𝑛𝜙𝑘(𝑤, 𝑤)
e.g. for a primary field 𝜙(𝑤, 𝑤), we have (another definition of primary fields)
𝑇 𝑧 𝜙 𝑤, 𝑤 =
ℎ 𝜙(𝑤, 𝑤)
𝑧 − 𝑤 2
+
𝜕𝑤𝜙 𝑤, 𝑤
𝑧 − 𝑤
+ regular
𝑇 𝑧 𝜙 𝑤, 𝑤 =
ℎ𝜙(𝑤, 𝑤)
𝑧 − 𝑤 2
+
𝜕𝑤𝜙 𝑤, 𝑤
𝑧 − 𝑤
+ regular
and for 𝑇 𝑧 𝑇(𝑤), we have;
𝑇 𝑧 𝑇 𝑤 =
𝑐/2
𝑧 − 𝑤 4
+
2 𝑇(𝑤)
𝑧 − 𝑤 2
+
𝜕𝑤𝑇 𝑤
𝑧 − 𝑤
+ regular

12. Free boson 𝑋(𝑧, 𝑧)
 The free boson action is
𝑆 =
1
4𝜋
∫ 𝑑𝑧𝑑𝑧 𝜕𝑋. 𝜕𝑋
 Equation of motion is
𝜕𝜕𝑋 = 0 ⇒ 𝜕𝑗 𝑧 = 𝜕𝑗 𝑧 = 0
𝑗 𝑧 = 𝑖𝜕𝑋(𝑧, 𝑧)
𝑗 𝑧 = 𝑖𝜕𝑋(𝑧, 𝑧)
 ℎ 𝑋 = 0 and ℎ 𝑗 = ℎ 𝑗 = 1 (𝑗 and 𝑗 are primary fields)
𝑗 𝑧 =
𝑛
𝑧−𝑛−1𝑗𝑛 𝑗 𝑧 =
𝑚
𝑧−𝑚−1𝑗𝑚
 𝐿𝑛 and 𝑗𝑚’s are connected as
𝐿𝑛 =
𝑘≻−1
𝑗𝑛−𝑘𝑗𝑘 +
𝑘≤−1
𝑗𝑘𝑗𝑛−𝑘
𝑐 = 1 (by calculating [𝐿𝑛, 𝑗𝑚] and ⟨0|𝐿2𝐿−2|0⟩)
𝑋(𝑧, 𝑧) is expanded as
𝑋 𝑧, 𝑧 = 𝑥0 − 𝑖 𝑗0 ln 𝑧𝑧 + 𝑖
𝑛≠0
1
𝑛
𝑗𝑛𝑧−𝑛
+ 𝑗𝑛𝑧−𝑛
(𝑗0 = 𝑗0)

13. Introducing a boundary
We can introduce a boundary at Im z = 0.
 We study it on a ‘strip’ with coordinates 𝜎 and 𝜏.

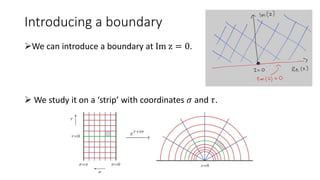
14. Free boson on the strip
 For variation of action to vary, we have;
∫ 𝑑𝜏 𝜕𝜎𝑋 𝛿𝑋
𝜎=0
𝜎=𝜋
= 0 ⇒
𝜕𝜎𝑋
𝜎=0,𝜋
= 0 (Neumann)
𝛿𝑋
𝜎=0,𝜋
= 𝜕𝜏𝑋
𝜎=0,𝜋
= 0 (Dirichlet)
𝑗𝑛 − 𝑗𝑛 = 0 Neumann − Neumann 𝑗𝑛 + 𝑗𝑛 = 0 Dirichlet − Dirichlet [𝑛 ∈ ℤ]
𝑗𝑛 − 𝑗𝑛 = 0 Neumann − Dirichlet 𝑗𝑛 + 𝑗𝑛 = 0 Dirichlet − Neumann 𝑛 ∈ ℤ +
1
2
 We have 𝐿𝑛 = 𝐿𝑛 which implies 𝑇 𝑧 = 𝑇(𝑧).

15. World Sheet duality
 Make the 𝜏 direction
compact
 We have the world sheet
duality (open closed duality)
𝜏, 𝜎 open → 𝜎, 𝜏 closed
The concept of Boundary
State arises

16. Boundary states
 Boundary conditions translate as follows (gluing conditions)
𝜕𝜏𝑋closed
𝜏=0
𝐵𝑁 = 0 𝜕𝜎𝑋closed
𝜏=0
𝐵𝐷 = 0
⇒ 𝑗𝑛 + 𝑗−𝑛 𝐵𝑁 = 0 (𝑗𝑛 − 𝑗−𝑛) 𝐵𝐷 = 0
 The solution of gluing conditions is as follows;
𝐵𝑁,𝐷 =
1
𝒩𝑁,𝐷
𝑚
𝑚 ⊗ |𝑈𝑚⟩
where
𝑚 =
𝑘=1
∞
1
𝑚𝑘
𝑗−𝑘
𝑘
𝑚𝑘
0 𝑈𝑐𝑈−1
= 𝑐∗
𝑈𝑗𝑘𝑈−1
=
𝑗𝑘 (Dirichlet)
−𝑗𝑘 (Neumann)
 Conformal symmetry requires (𝐿𝑛−𝐿−𝑛)|𝐵𝑁,𝐷⟩ = 0

17. Constraint on Boundary States
 In open sector, we calculate the partition function
𝑍 𝑡 = 𝑇𝑟ℋ 𝑞𝐿0−
1
24 where 𝑞 = 𝑒−2𝜋𝑡
 In the closed string sector, we calculate the amplitude
𝑍 𝑙 = ⟨Θ𝐵|𝑒
−2𝜋𝑙 𝐿0+𝐿0−
1
12 |𝐵⟩
Their equality gives us 𝒩D = 1, 𝒩N = 2
 For generalizing (and for without lagrangian) introduce Ishibashi states and a general
boundary state (𝜙𝑖 is a representation);
|ℬ𝑖⟩⟩ =
→
𝑚
𝜙𝑖, 𝑚 ⊗ 𝑈 𝜙𝑖, 𝑚 |𝐵𝛼⟩ =
𝑖
𝐵𝛼
𝑖 |ℬ𝑖⟩⟩
then 𝐵𝛼
𝑖
’s must satisfy a condition (Cardy condition)
𝑖
𝐵𝛼
𝑖
𝐵𝛽
𝑖
𝑆𝑖𝑗 ∈ ℤ0
+
∀ 𝑗

18. Sewing constraints
 We can generalize to arbitrary surfaces
(Riemann surfaces) with boundaries and holes.
 We calculate the correlation functions
0 𝜙1 𝑥1 … 𝜙𝑛 𝑥𝑛 𝜓1 𝑦1 … 𝜓𝑚(𝑦𝑚)|0⟩
by chopping off the surface into parts to get
three and lesser point functions.
 The answer shouldn’t depend on chopping
and we have Sewing constraints.
e.g. the first constraint is
𝐶12𝑞𝐶34𝑞𝑀
1 4
2 3 𝑞𝑟
= 𝐶14𝑟𝐶23𝑟𝑀
1 4
2 3 𝑟𝑞
where the matrices are called fusion matrices.

19. Free Compact Boson
 The compact boson follows the following condition
𝑋 𝑧, 𝑧 ∼ 𝑋 𝑧, 𝑧 + 2𝜋𝑅𝑛 𝑛 ∈ ℤ
⇒ 𝑋 𝑒2𝜋𝑖
𝑧, 𝑒−2𝜋𝑖
𝑧 = 𝑋 𝑧, 𝑧 + 2𝜋𝑅𝑛 ⇒ 𝑗0 − 𝑗0 = 𝑅𝑛
 The action of 𝑗0 and 𝑗0 is non-trivial on vacuum |Δ, 𝑛⟩
𝑗0 Δ, 𝑛 = Δ Δ, 𝑛 , 𝑗0 Δ, 𝑛 = (𝑅𝑛 − Δ)|Δ, 𝑛⟩
 Modular invariance gives
Δ =
𝑚
𝑅
+
𝑅𝑛
2
⇒ 𝑗0 Δ, 𝑛 =
𝑚
𝑅
+
𝑅𝑛
2
𝑚, 𝑛 , 𝑗0 Δ, 𝑛 =
𝑚
𝑅
−
𝑅𝑛
2
|𝑚, 𝑛⟩
 The possible Ishibashi states are |𝑚, 0⟩⟩, |0, 𝑛⟩⟩ and the states |𝐽⟩⟩ where 𝐽 = 0,1,2, …
(The |𝐽⟩⟩ states correspond to vertex operators)
 A general boundary state is as follows
𝛼 =
𝐽=1
∞
𝐵𝐽
𝛼
|𝐽⟩⟩ +
𝑚∈ℤ/{0}
∞
𝐵𝑚
𝛼
|𝑚, 0⟩⟩ +
𝑛∈ℤ/{0}
∞
𝐵𝑛
𝛼
|0, 𝑛⟩⟩

20. The irrational
𝑅
𝑅self dual
case
 If 𝑅/𝑅self dual is irrational where;
𝑅self dual = 2𝑘 𝑘 ∈ 𝑍+
then Dirichlet and Neumann boundary states are
𝑁 𝜃 =
𝐽=0
∞
−1 𝐽
|𝐽⟩⟩ +
𝑛∈ℤ/{0}
∞
𝑒𝑖𝑛𝜃
|0, 𝑛⟩⟩
𝐷 𝜃 =
𝐽=0
∞
|𝐽⟩⟩ +
𝑚∈ℤ/{0}
∞
𝑒𝑖𝑚𝜃
|𝑚, 0⟩⟩
 There is also a set of so-called Friedan boundary states |𝑥⟩
𝑥 =
𝑙=0
∞
𝑃𝑙 𝑥 |𝑙⟩⟩
The form is proven by recursion relations (using the first Sewing constraint).

21. Analogue of Cardy condition in
𝑅
𝑅self dual
case
 Recall that Cardy condition is
Amplitude in closed = Partition function in open string channel
string channel with nonnegative coefficients
 We calculate amplitude with | cos 𝜃1⟩ and | cos 𝜃2⟩ as boundary states to get
𝑍closed =
𝑙=0
∞
𝑃𝑙(cos 𝜃1) 𝑃𝑙(cos 𝜃2)𝜒𝑙2
Vir
𝑞
In the open string channel, it can be written as
𝑍open =
1
𝜋2 2 0
𝜋
𝑑𝜙2
0
𝜋
𝑑𝜙
𝑛=−∞
∞
𝜒1
4
𝑛+
𝑡
2𝜋
2(𝑞)
Where
cos
𝑡
2
= cos
𝜃
2
cos
𝜙
2
cos 𝜃 = cos 𝜃1 cos 𝜃2 − sin 𝜃1 sin 𝜃2 cos 𝜙2
 So we get a positive definite measure instead of non negative coefficients in Cardy condition.

22. Questions
 What are these Friedan states
𝑥 =
𝑙=0
∞
𝑃𝑙 𝑥 |𝑙⟩⟩
In terms of the field 𝑋(𝑧, 𝑧) (i.e. write them as 𝑗𝑛’s acting on |0⟩).
How to interpret Cardy’s condition in irrational 𝑅/𝑅self dual case?
 What happens when we study the irrational 𝑅/𝑅self dual case on a ℤ2 orbifold
𝑋 𝑧, 𝑧 ∼ ℛ𝑋 𝑧, 𝑧 = −𝑋 𝑧, 𝑧 ⇒ ℛ 𝑚, 𝑛 = | − 𝑚, −𝑛⟩
 What about orbifolds with other group symmetry?

23. Thank you
for listening