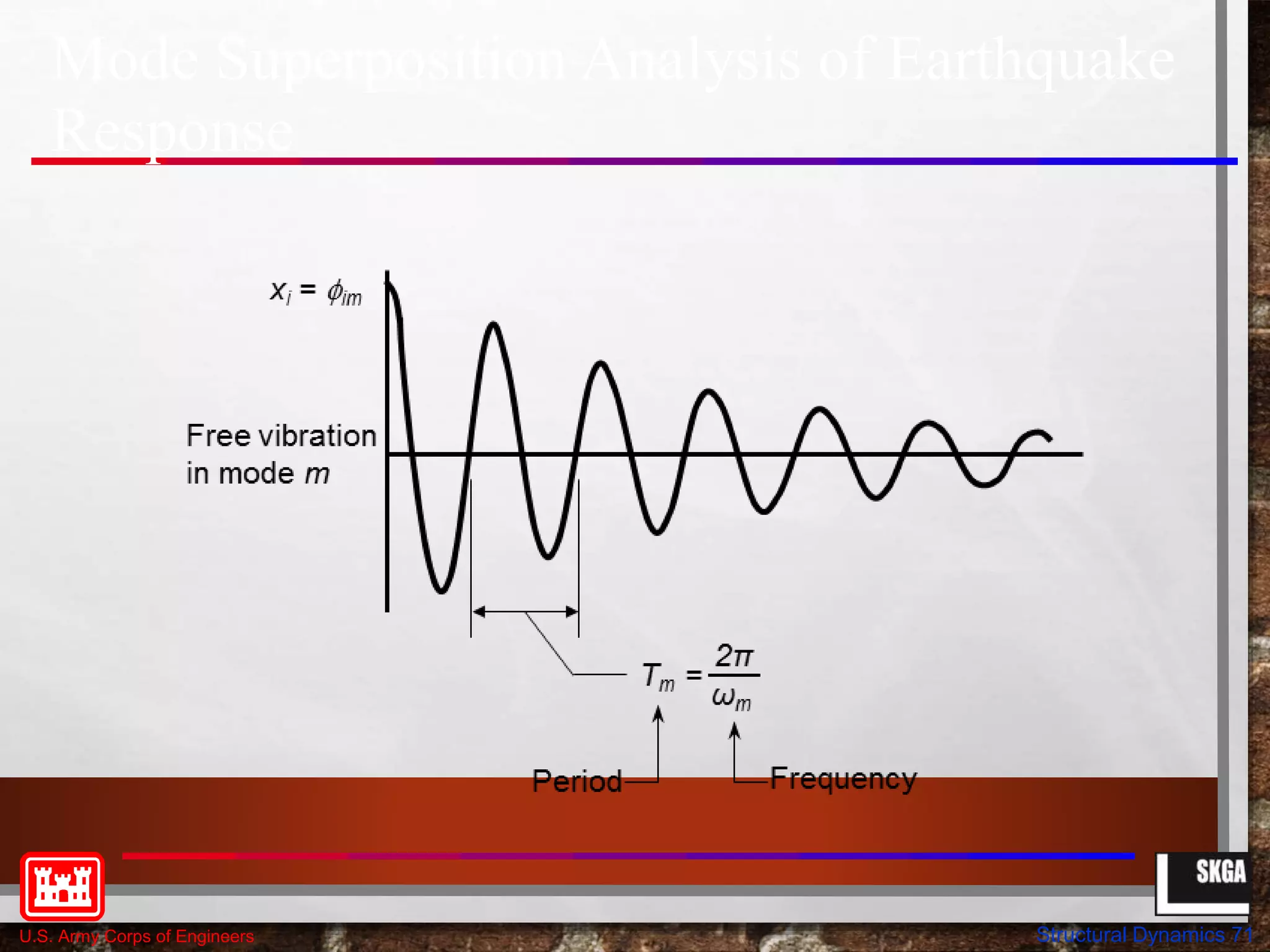
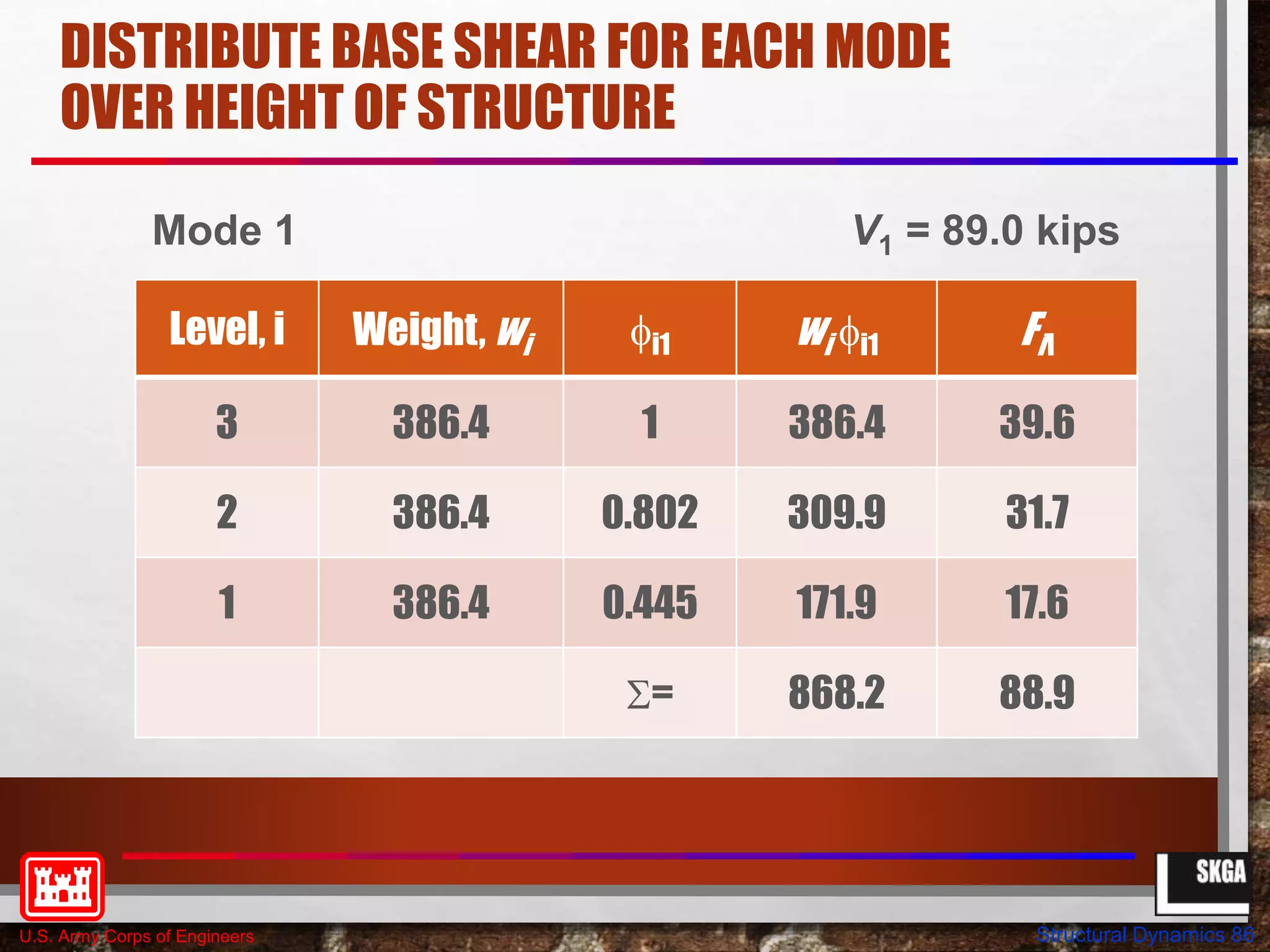
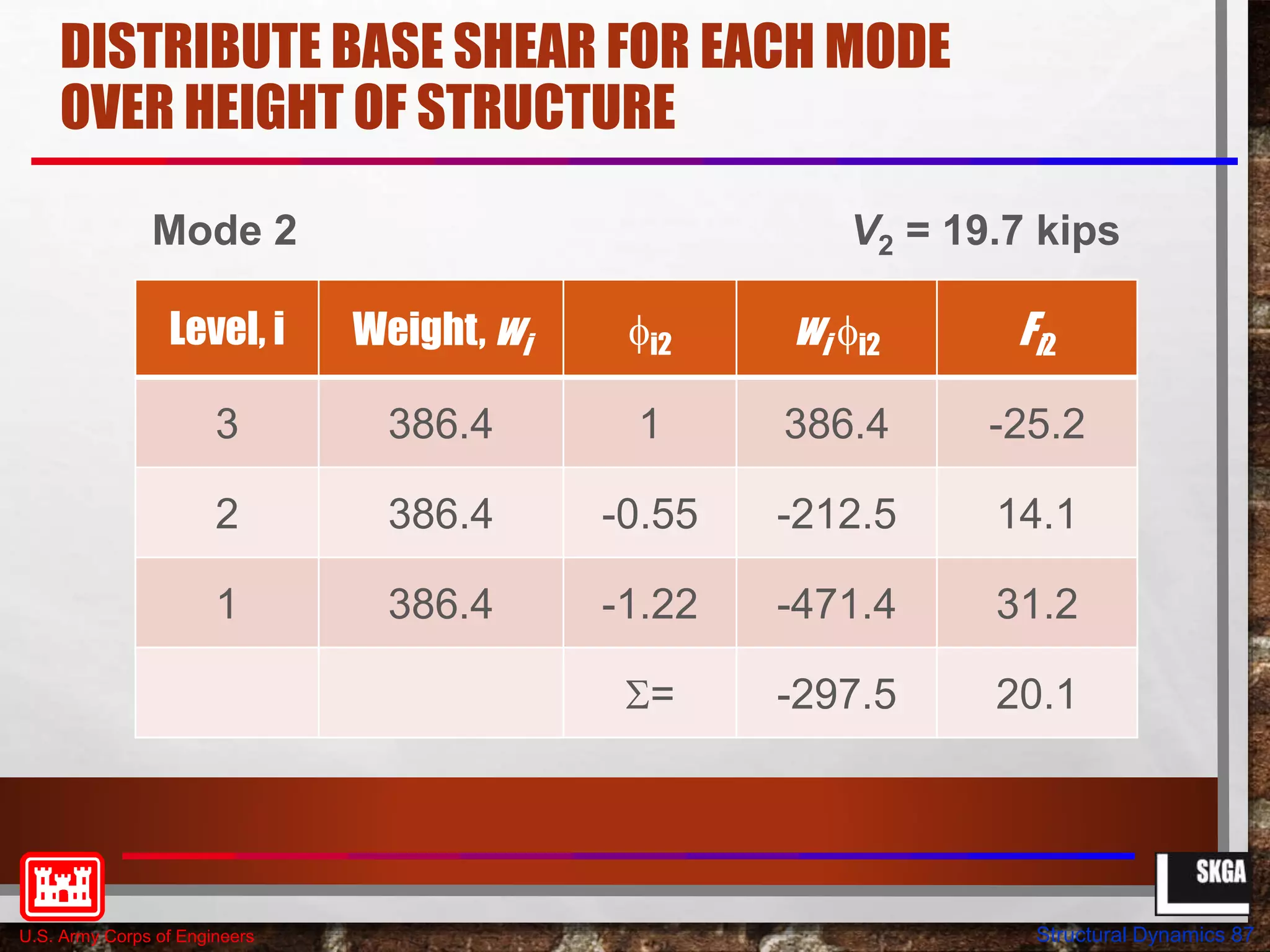
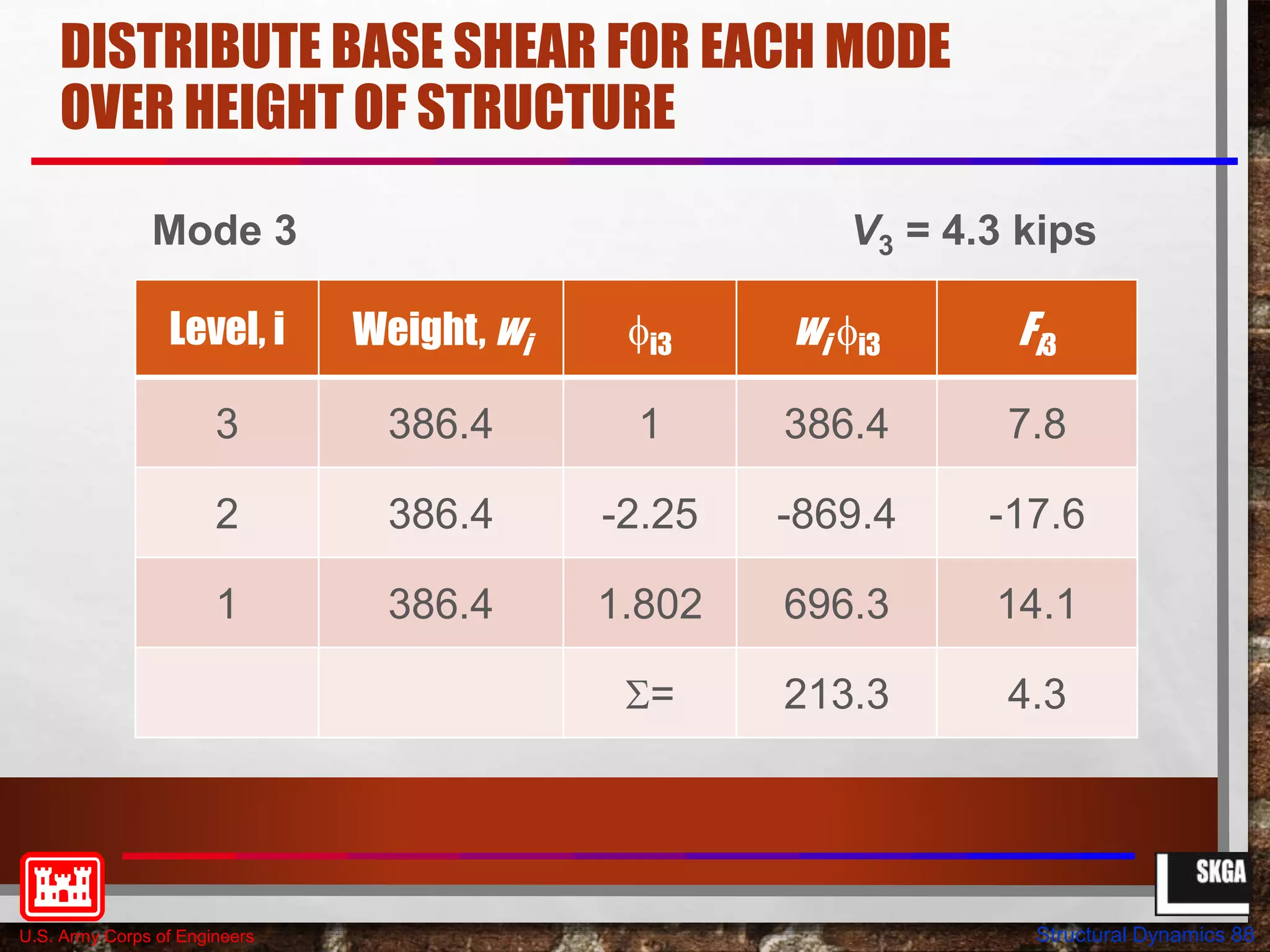
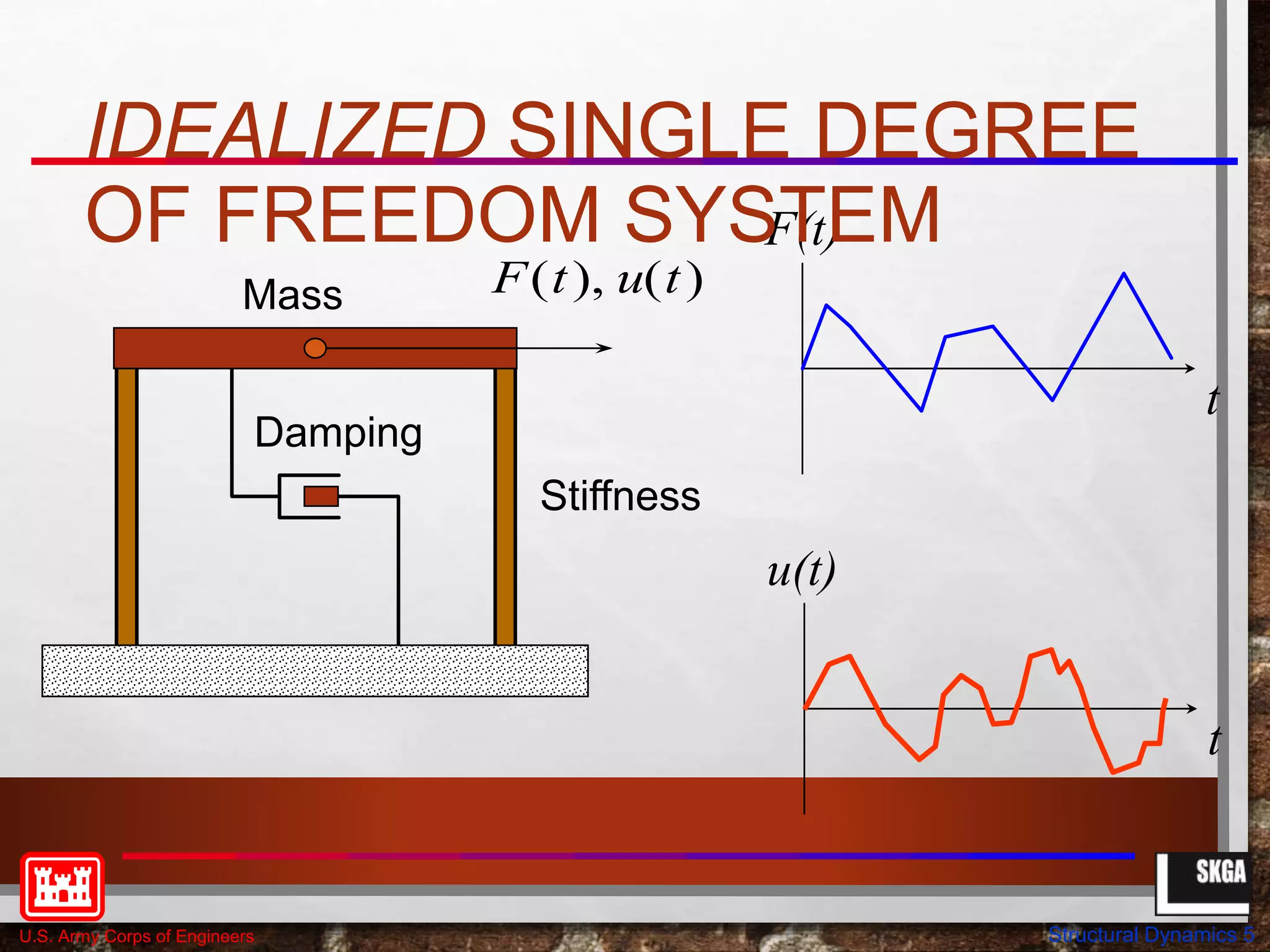
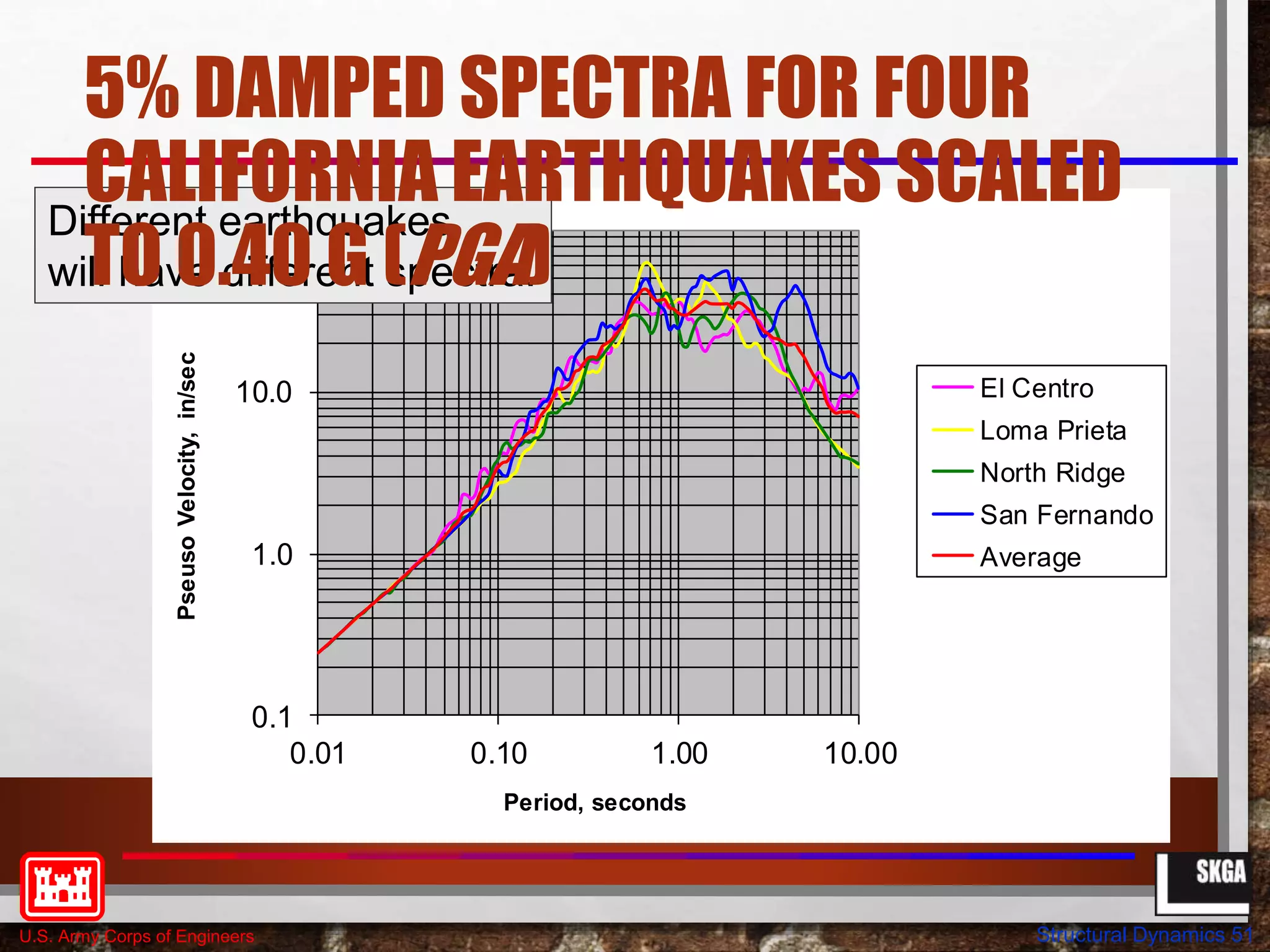
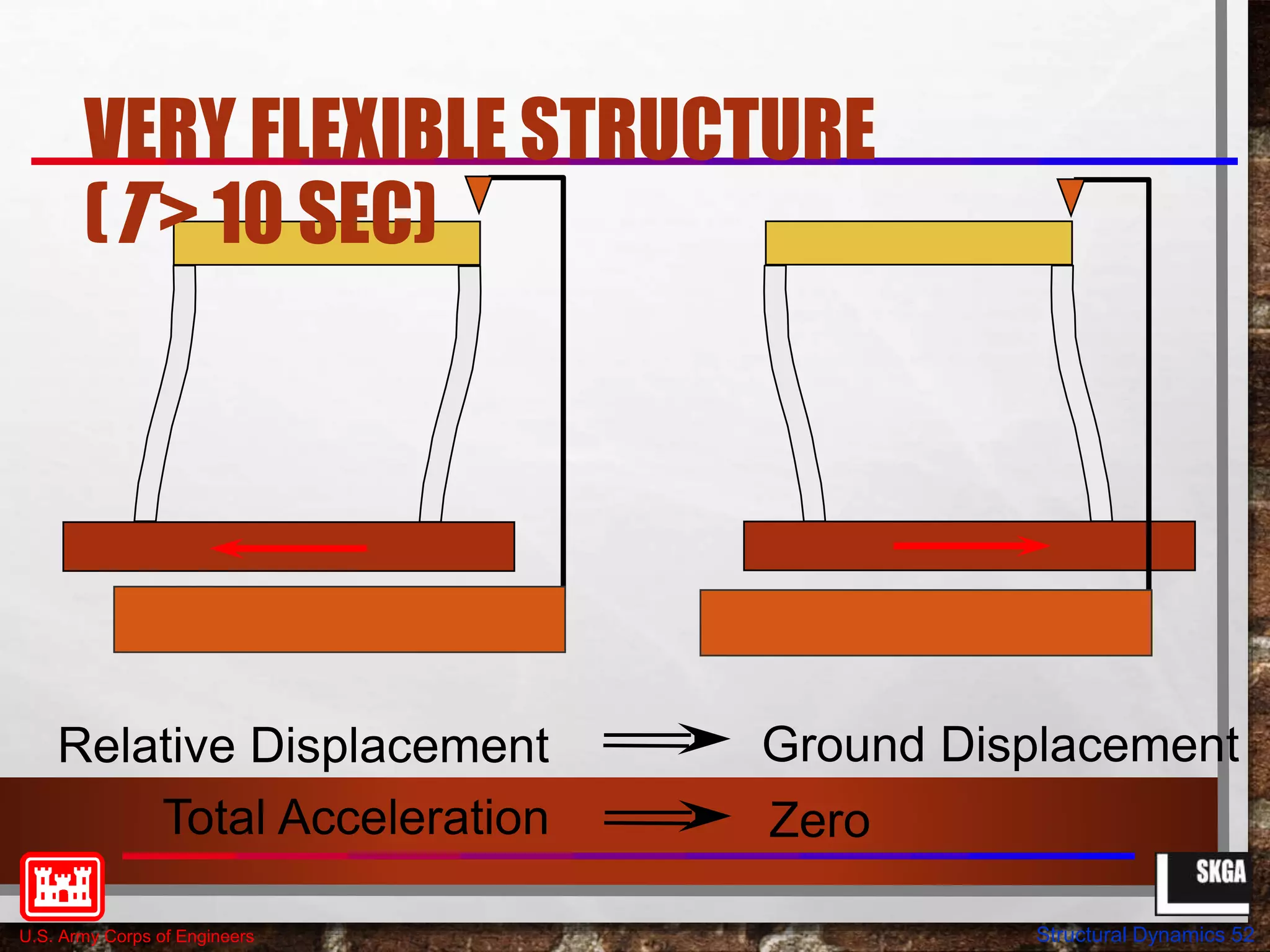
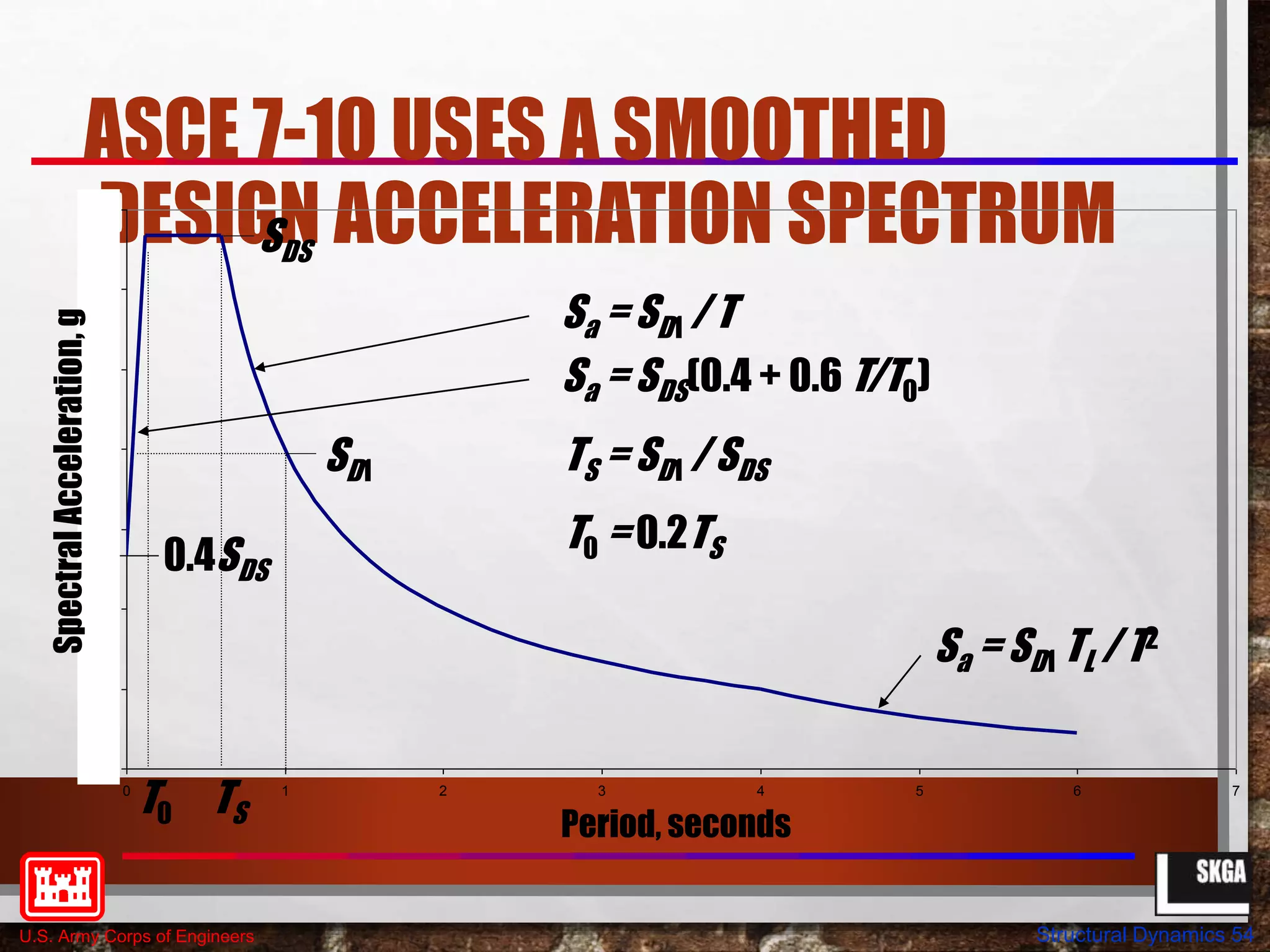
This document provides an overview of structural dynamics concepts for single degree of freedom systems. It covers equations of motion, natural frequency and period of vibration, dynamic amplification, and the effects of damping. Key concepts discussed include linear elastic response spectra and how damping affects resonant response under harmonic loading. The objectives are to provide an understanding of seismic structural response in terms of structural dynamics and how code-based seismic design is based on these principles.





![U.S. Army Corps of Engineers Structural Dynamics 13
)]
t
sin(
u
u
)
t
cos(
u
[
e
)
t
(
u D
D
D
t
ω
ω
ξω
+
+
ω
= 0
0
0
ξω
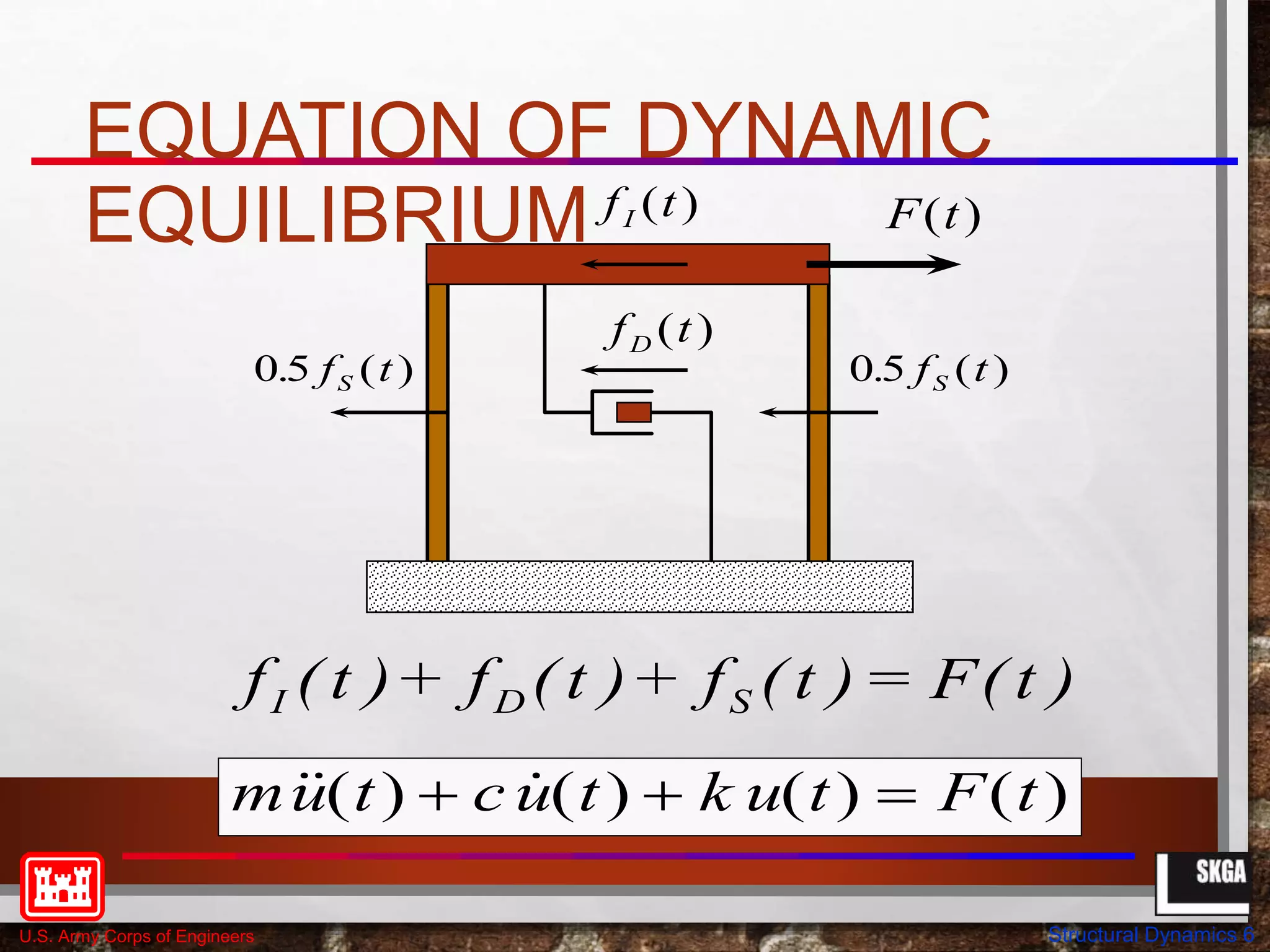
mu t c u t k u t
( ) ( ) ( )
0
Equation of Motion:
0
0u
u
Initial Conditions:
Solution:
c
c
c
m
c
=
ω
2
=
ξ
2
ξ
-
1
ω
=
ωD
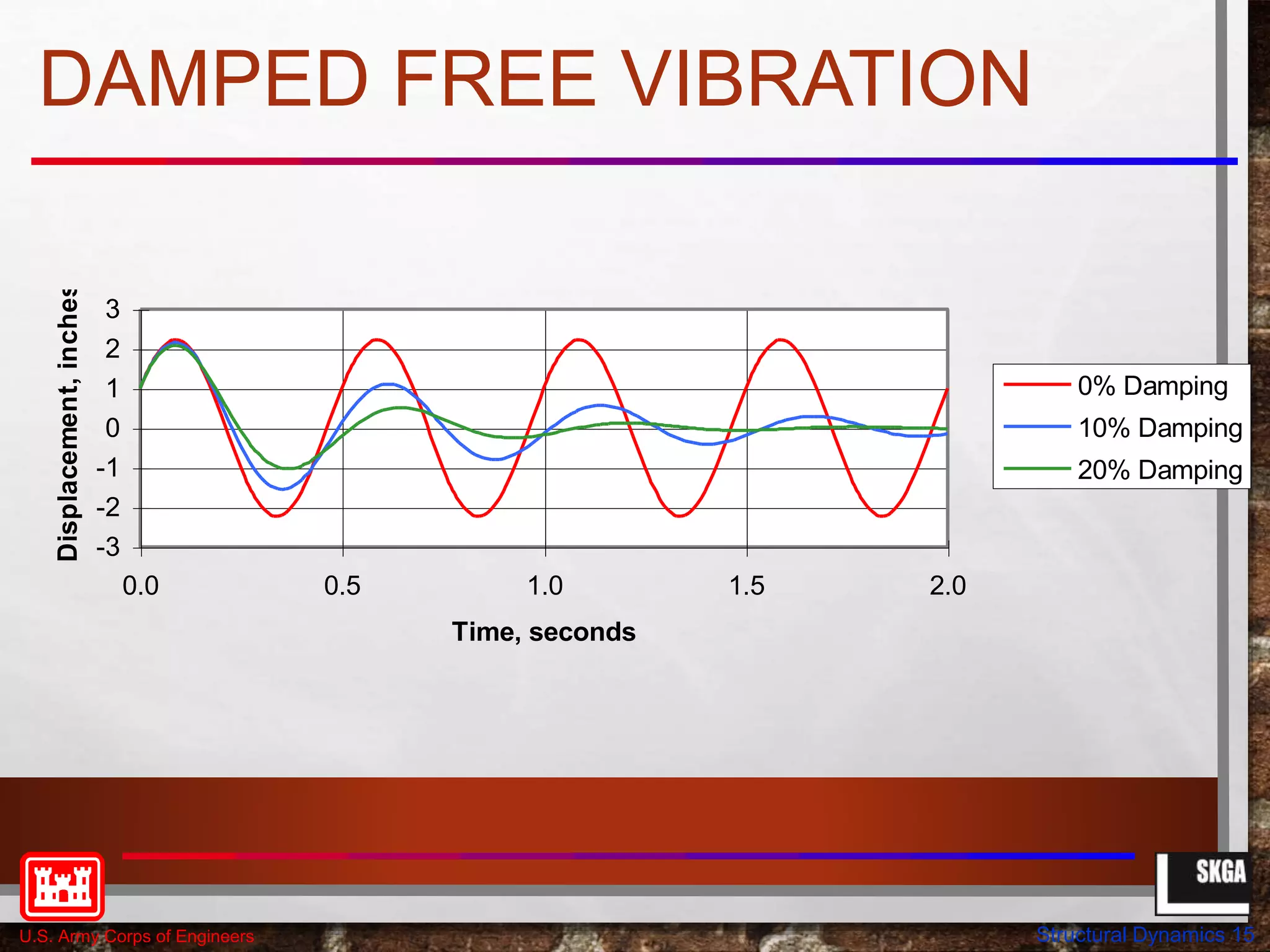
DAMPED FREE VIBRATION](https://image.slidesharecdn.com/structural-dynamics-230705120018-3a335f42/75/structural-dynamics-pptx-13-2048.jpg)



![U.S. Army Corps of Engineers Structural Dynamics 20
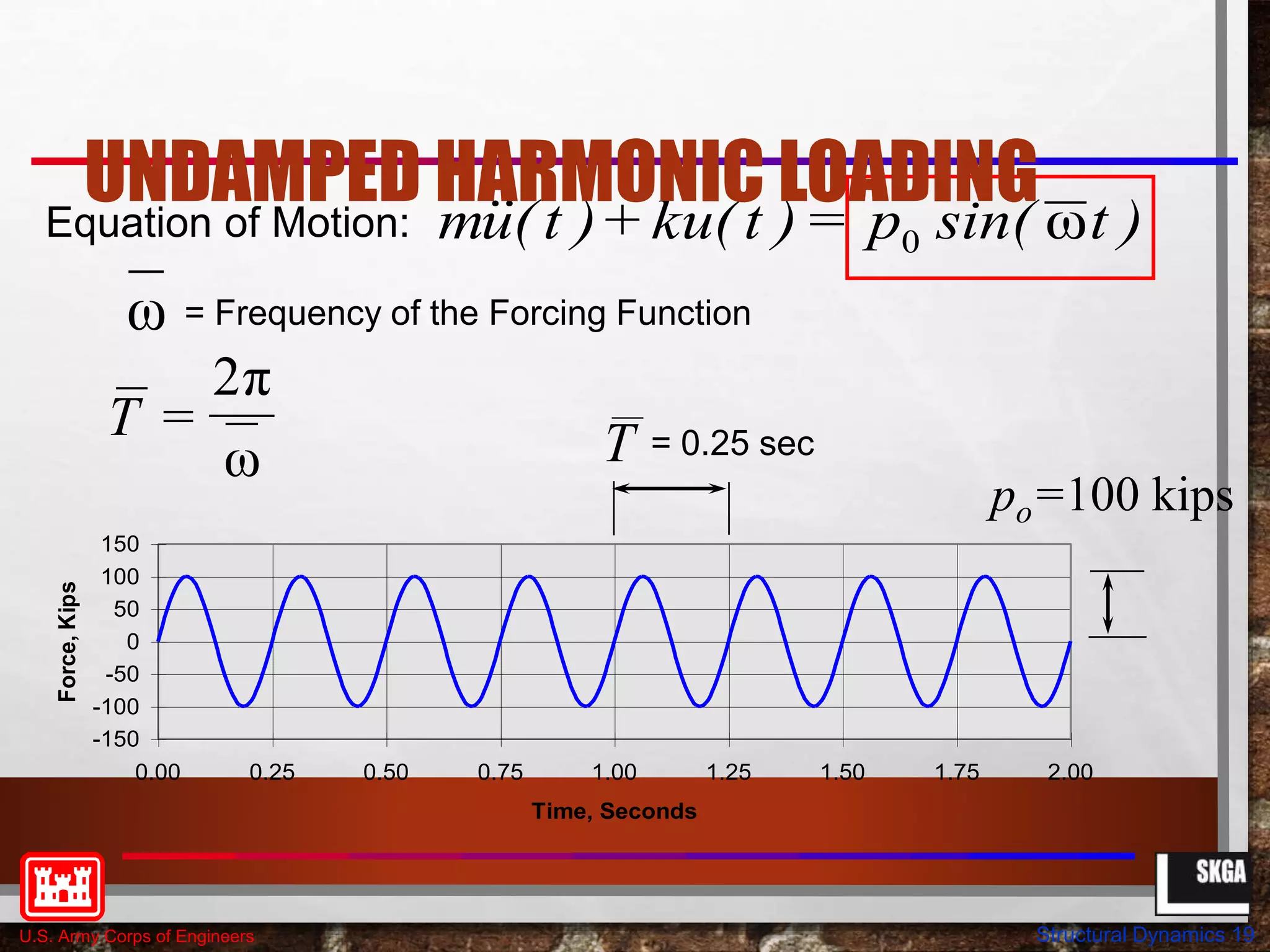
Solution:
)]
t
sin(
)
t
[sin(
)
/
(
k
p
)
t
(
u ω
ω
ω
-
ω
ω
ω
-
1
1
= 2
0
)
t
sin(
p
)
t
(
u
k
)
t
(
u
m ω
=
+ 0
Equation of Motion:
Assume system is initially at rest:
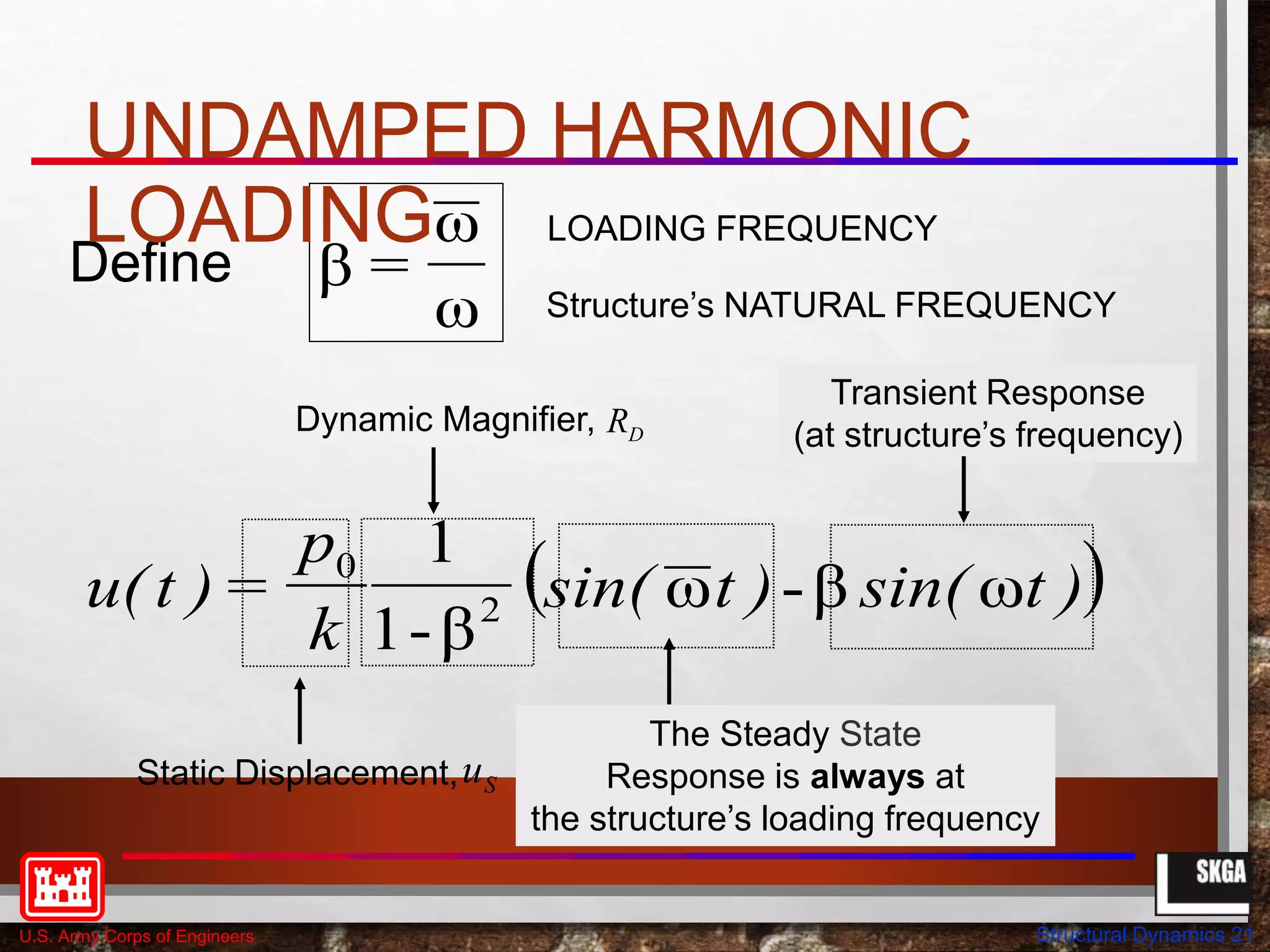
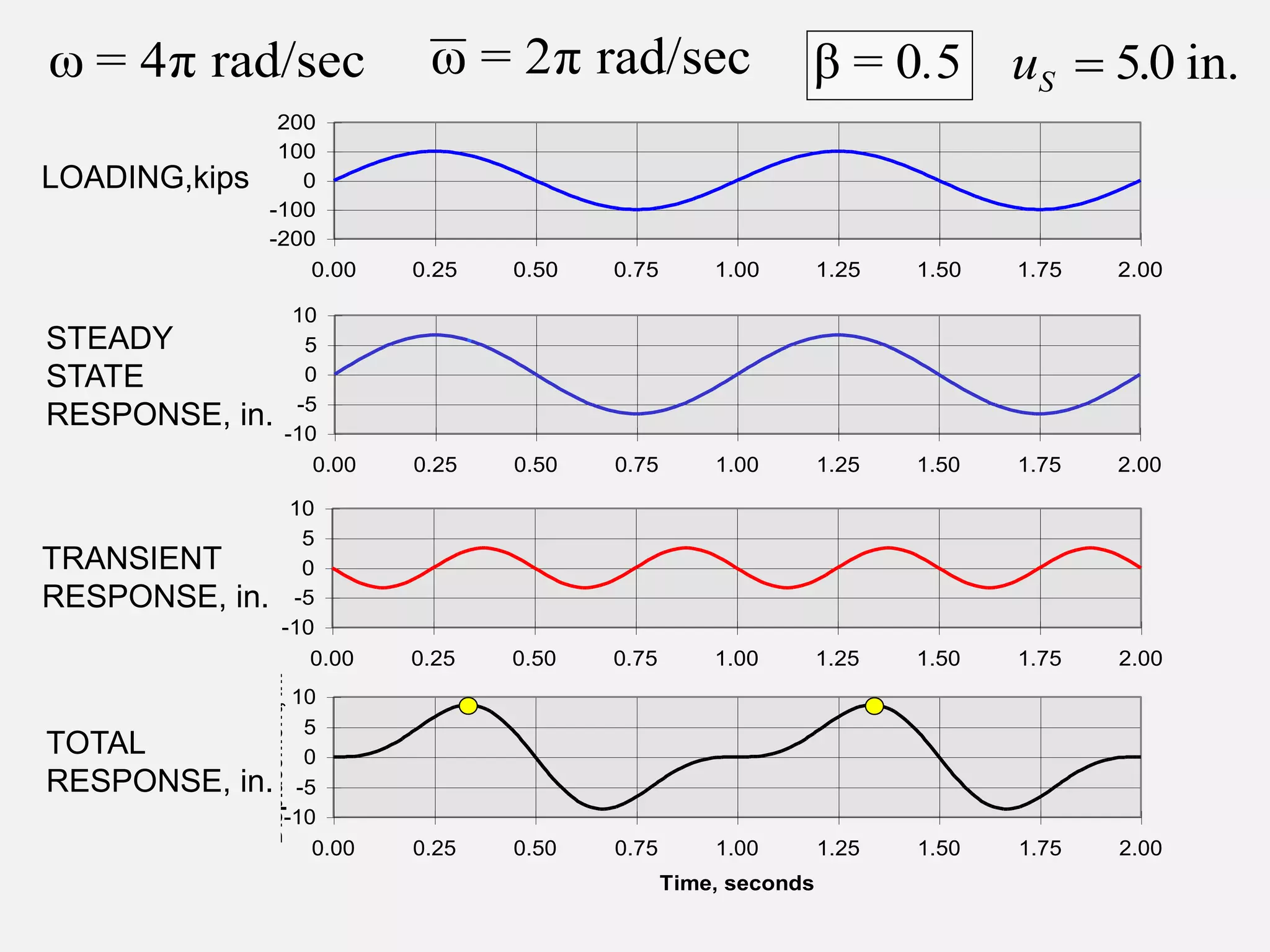
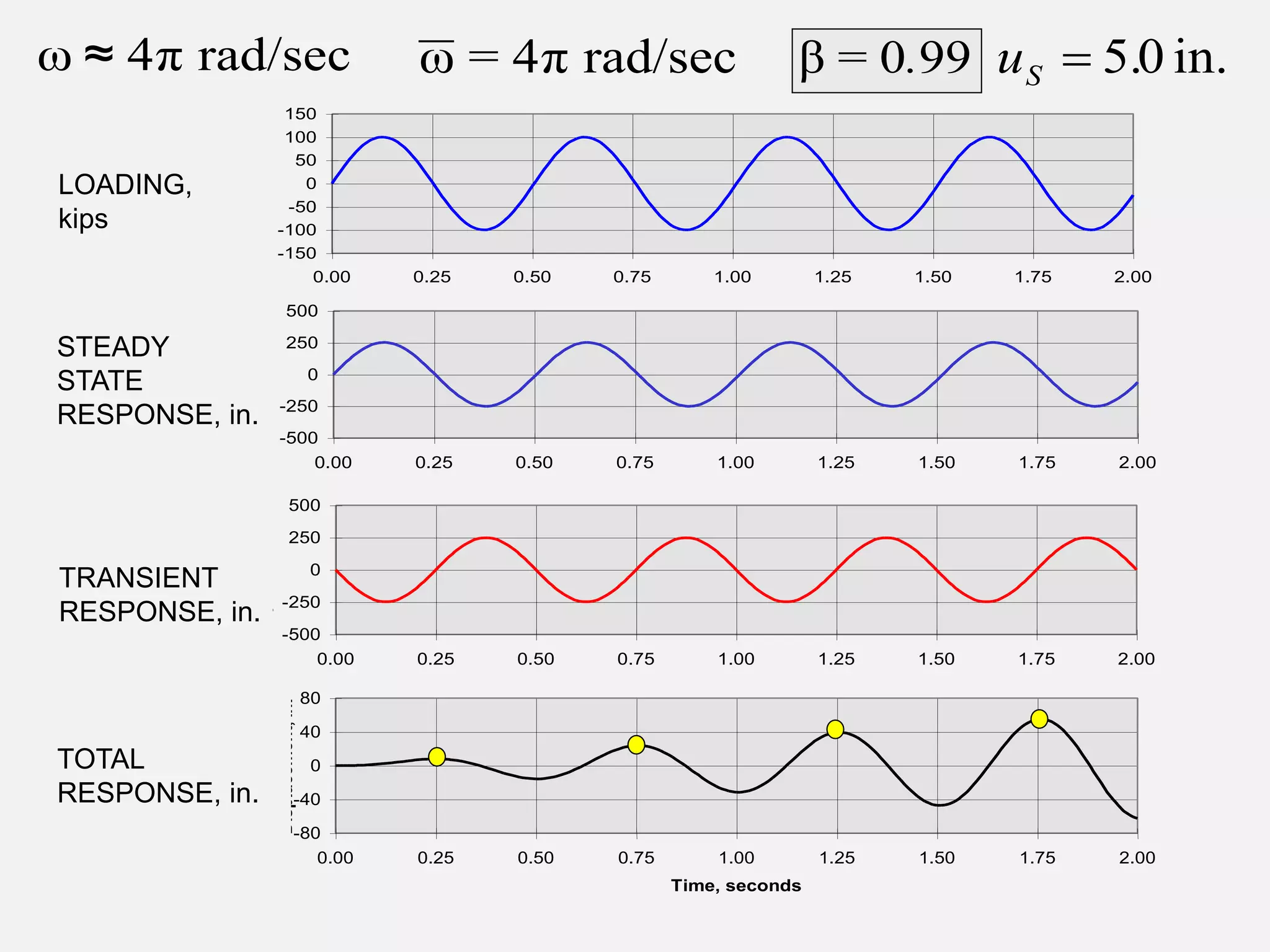
UNDAMPED HARMONIC
LOADING (2)](https://image.slidesharecdn.com/structural-dynamics-230705120018-3a335f42/75/structural-dynamics-pptx-20-2048.jpg)
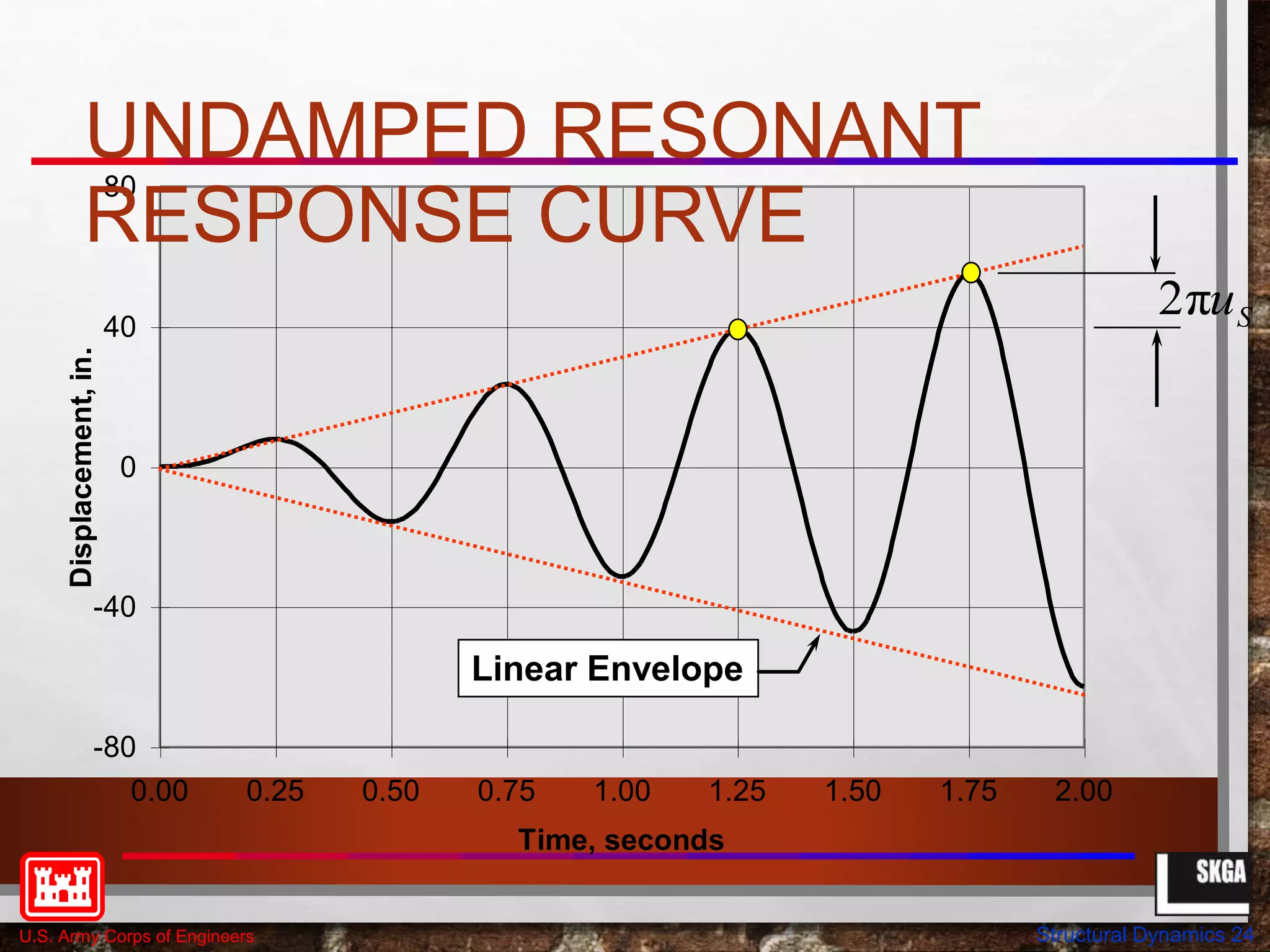
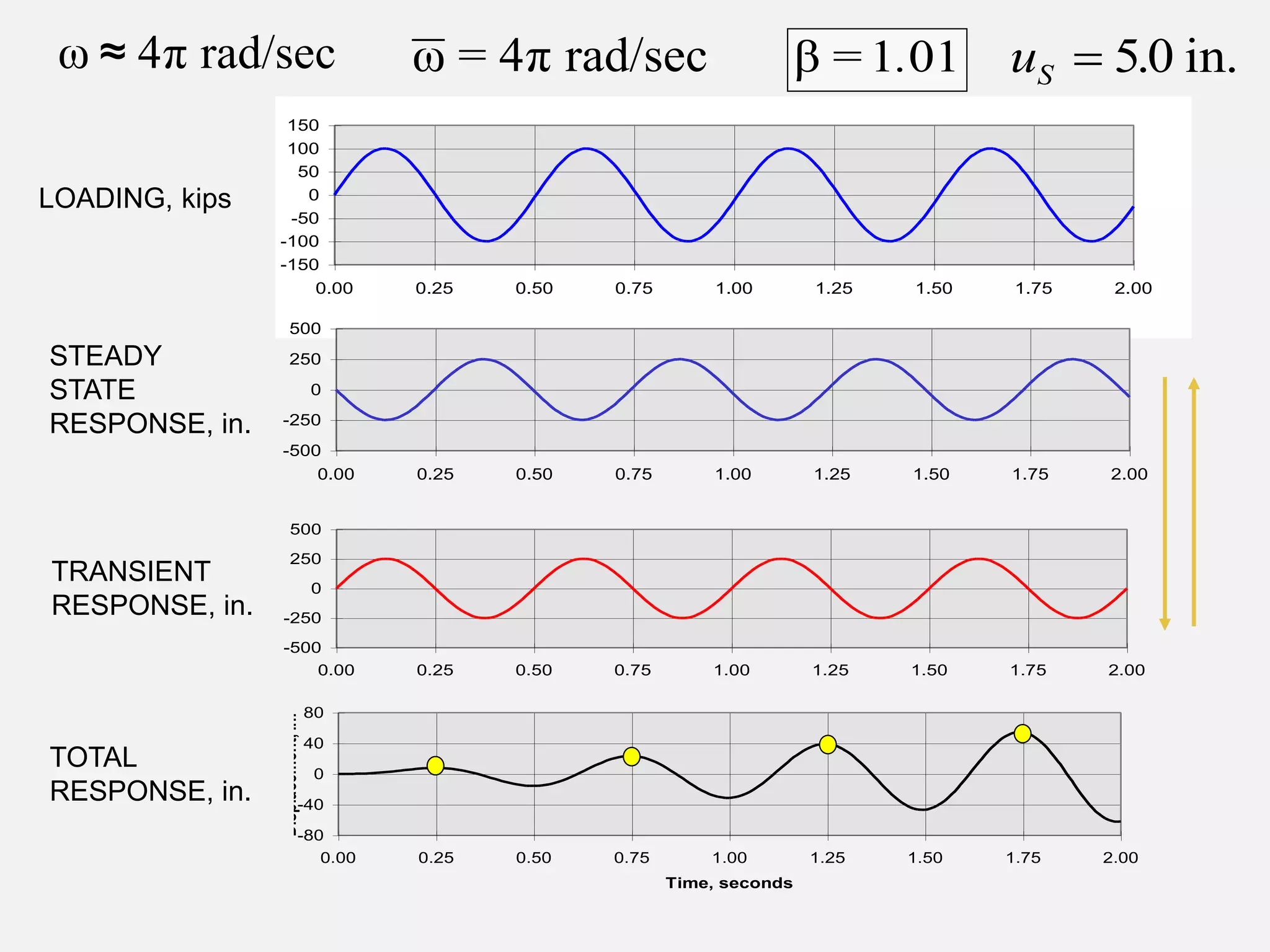
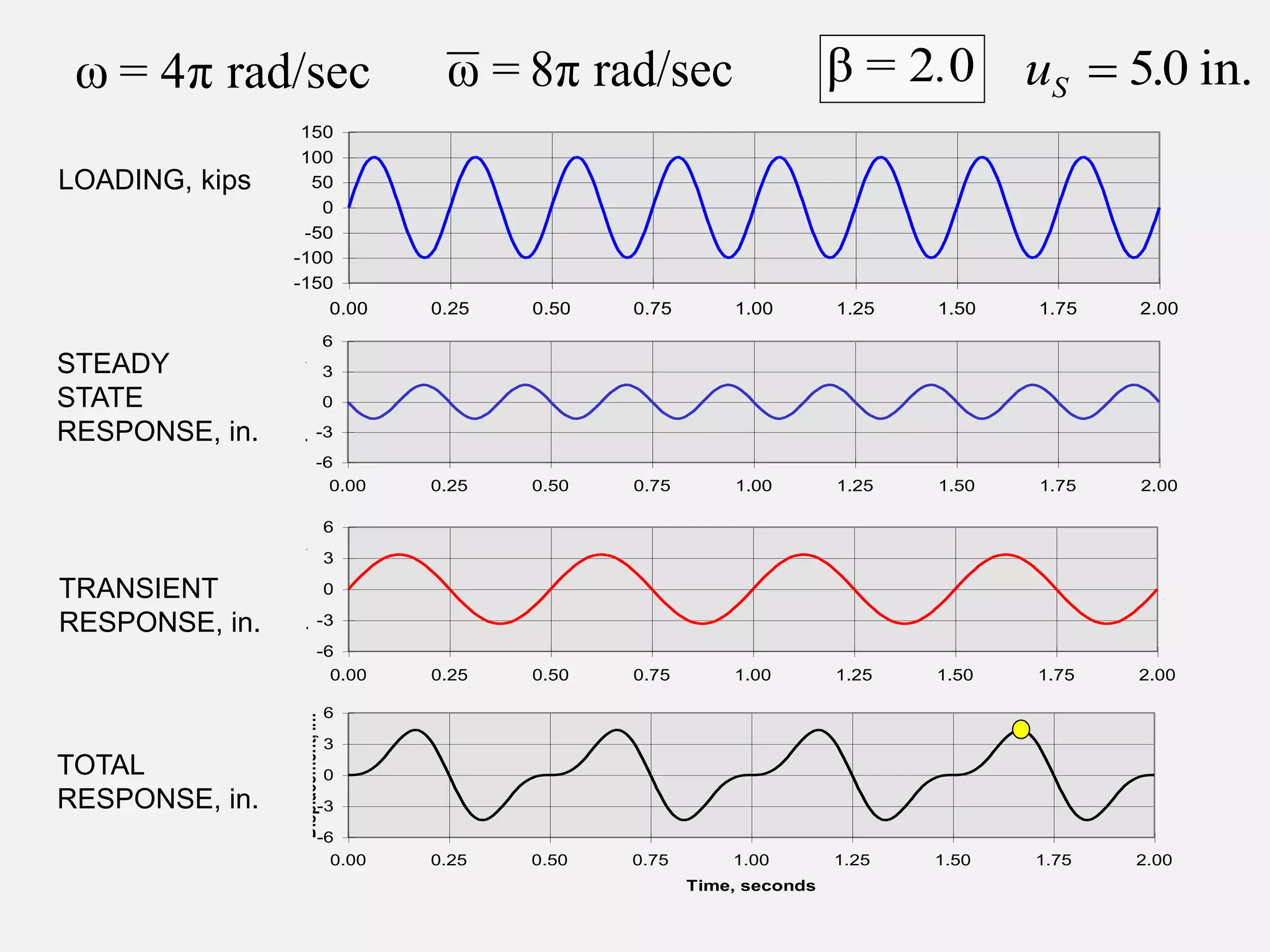
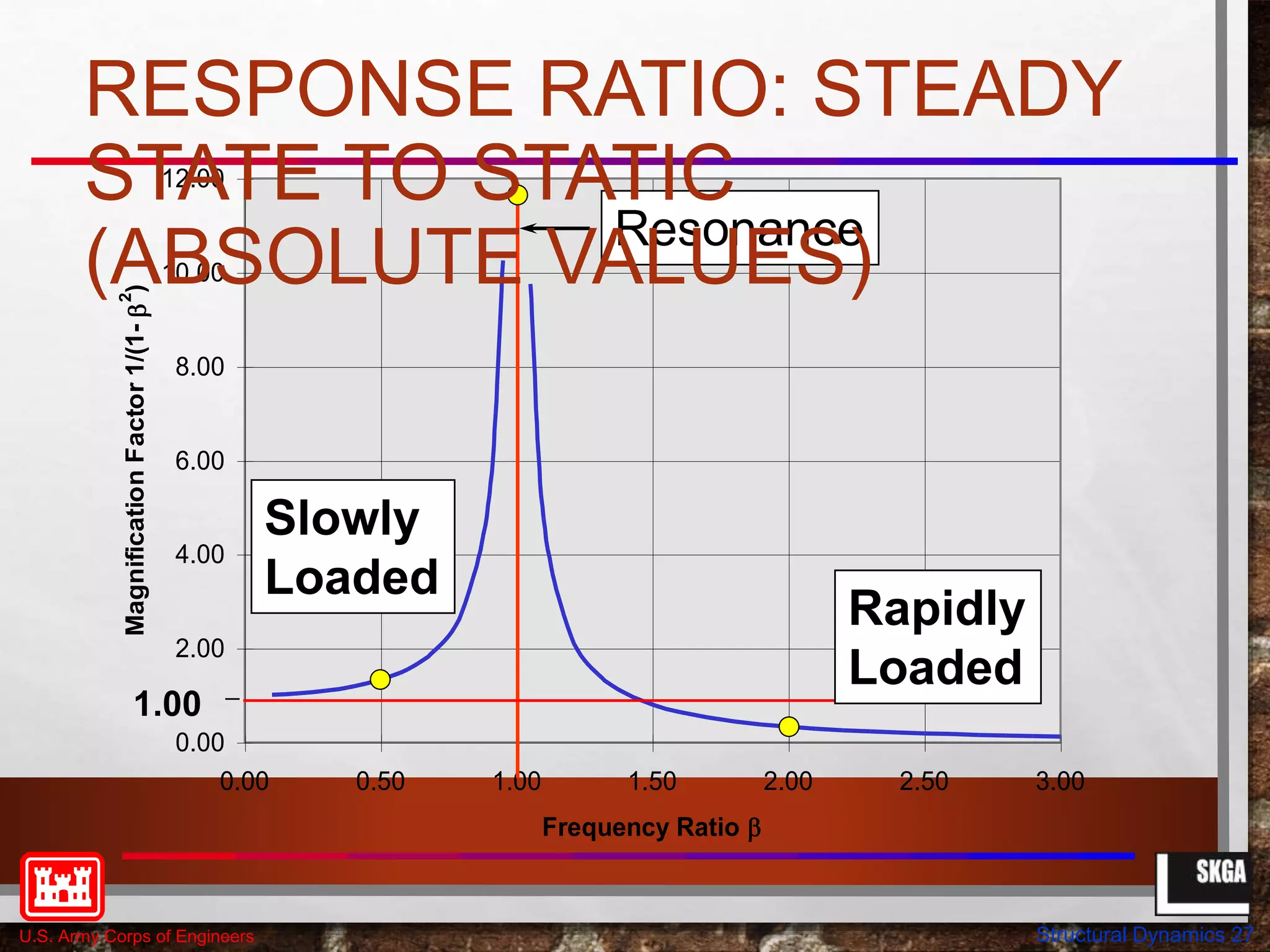



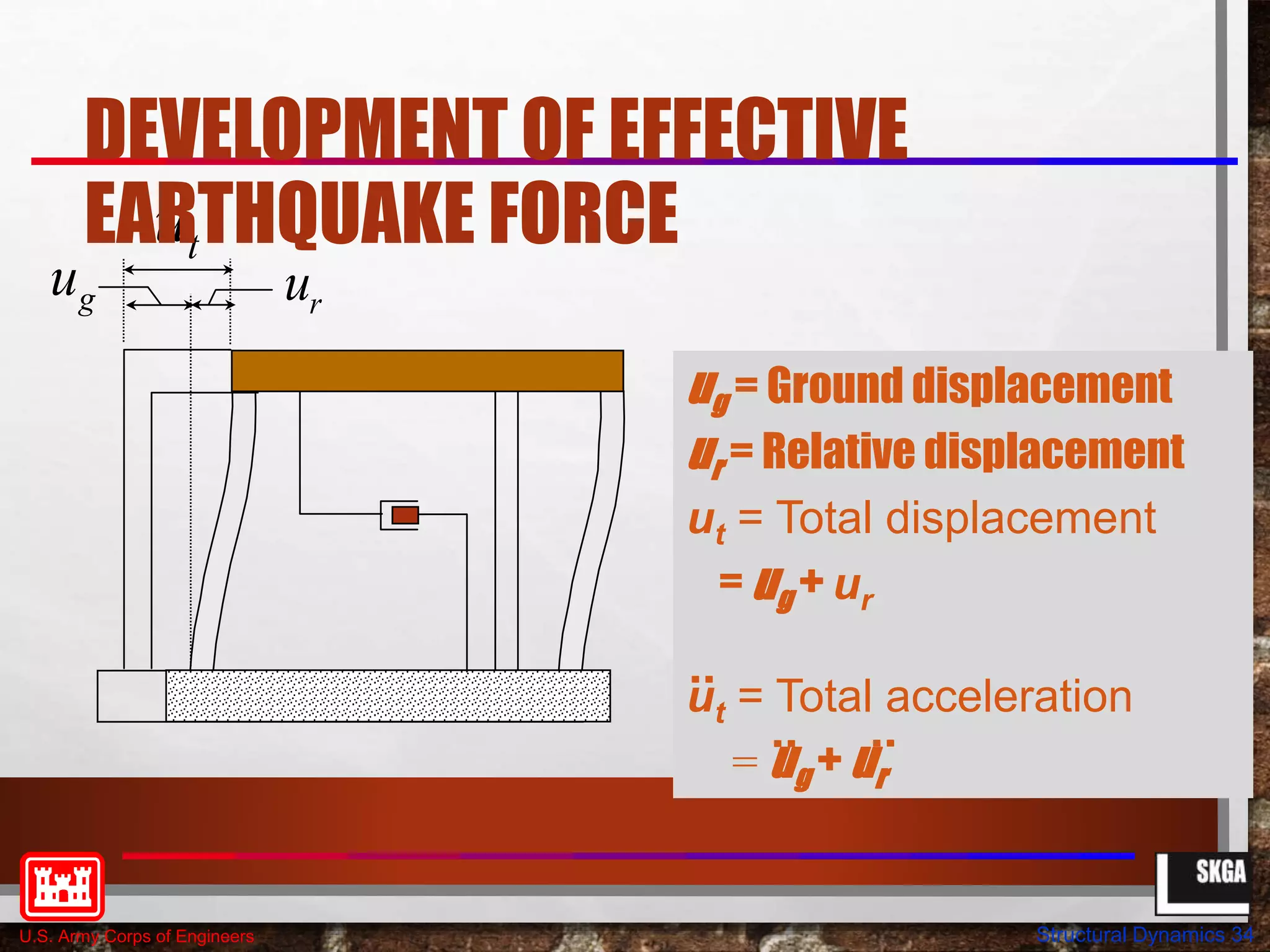
![U.S. Army Corps of Engineers Structural Dynamics 35
m u t u t cu t k u t
g r r r
[ ( ) ( )] ( ) ( )
0
mu t cu t k u t mu t
r r r g
( ) ( ) ( ) ( )
DEVELOPMENT OF EFFECTIVE
EARTHQUAKE FORCE
• INERTIA FORCE DEPENDS ON THE TOTAL ACCELERATION OF THE MASSES.
• RESISTING FORCES FROM STIFFNESS AND DAMPING DEPEND ON THE RELATIVE
DISPLACEMENT AND VELOCITY.
• THUS, THE EQUATION OF MOTION CAN BE WRITTEN AS:](https://image.slidesharecdn.com/structural-dynamics-230705120018-3a335f42/75/structural-dynamics-pptx-35-2048.jpg)








![U.S. Army Corps of Engineers Structural Dynamics 59
EQUATIONS OF MOTION
• FREE VIBRATION
[C] = [0], {P(T)} = {0}
0
r
r u
k
u
m
](https://image.slidesharecdn.com/structural-dynamics-230705120018-3a335f42/75/structural-dynamics-pptx-59-2048.jpg)

![U.S. Army Corps of Engineers Structural Dynamics 61
EQUATIONS OF MOTION
[ ]{ } [ ]{ } { }
[ ]{ } { }
0
=
ω
-
0
=
+
ω
2
2
A
m
k
A
k
A
m
-](https://image.slidesharecdn.com/structural-dynamics-230705120018-3a335f42/75/structural-dynamics-pptx-61-2048.jpg)


![U.S. Army Corps of Engineers Structural Dynamics 65
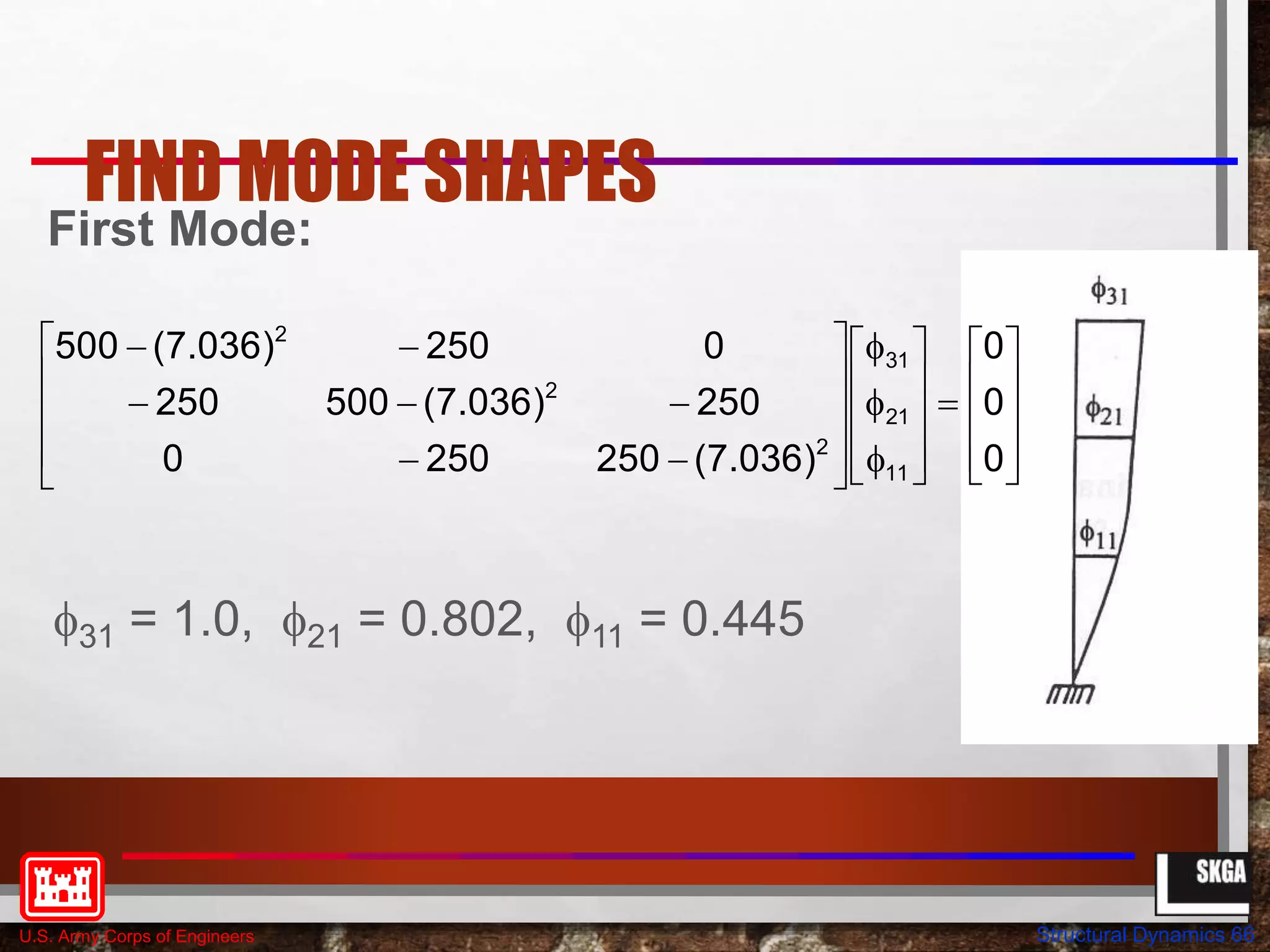
FIND DETERMINANT FOR MATRIX
[K] - w2[M]
w1 = 7.036 RADIANS/SEC.
w2 = 19.685 RADIANS/SEC.
w3 = 28.491 RADIANS/SEC.
The period is equal
to 2p/w:
T1 = 0.893 sec.
T2 = 0.319 sec.
T3 = 0.221 sec.
Setting the determinant of
the above matrix equal to
zero yields the following
frequencies:
w
w
w
w
2
2
2
2
250
250
0
250
500
250
0
250
500
m
k](https://image.slidesharecdn.com/structural-dynamics-230705120018-3a335f42/75/structural-dynamics-pptx-65-2048.jpg)


![U.S. Army Corps of Engineers Structural Dynamics 69
Orthogonality Properties of
Natural Mode Shapes
The natural modes of vibration of any multi degree of
freedom system are orthogonal with respect to the mass
and stiffness matrices. The same type of orthogonality can
be assumed to apply to the damping matrix as well:
{m}T[m] {n} = 0
{m}T[c] {n} = 0 for m ≠ n
{m}T[k] {n} = 0](https://image.slidesharecdn.com/structural-dynamics-230705120018-3a335f42/75/structural-dynamics-pptx-69-2048.jpg)