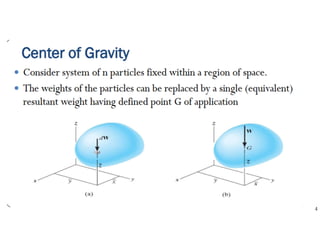
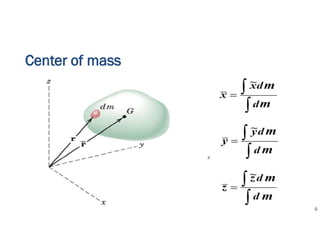
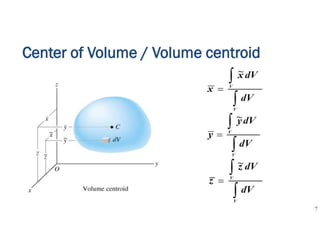
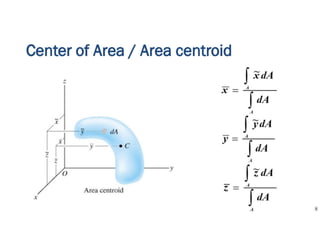
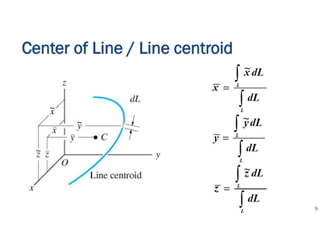
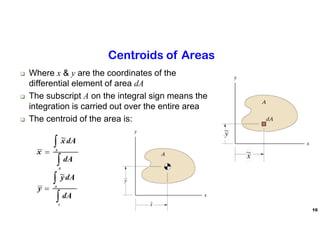
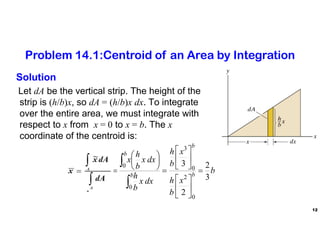
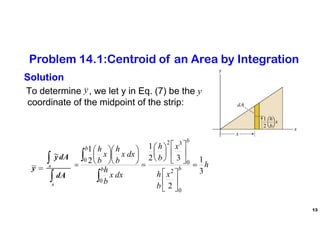
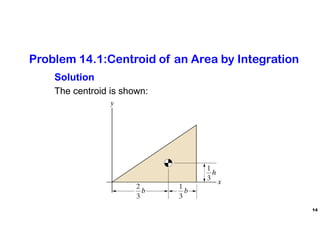
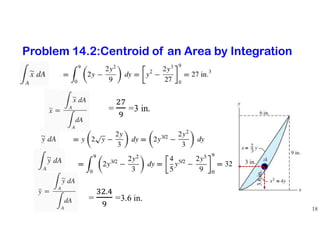
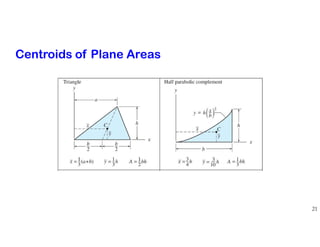
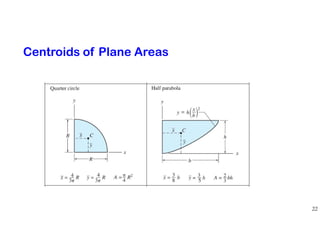
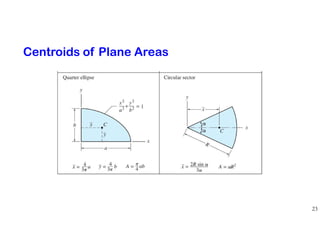
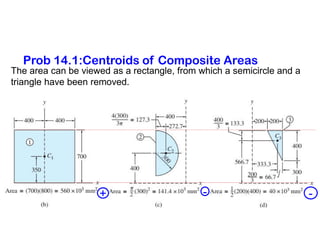
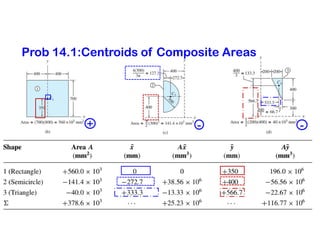
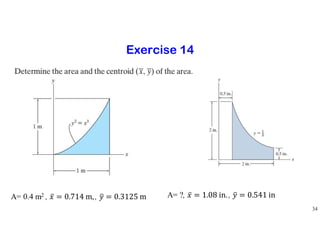
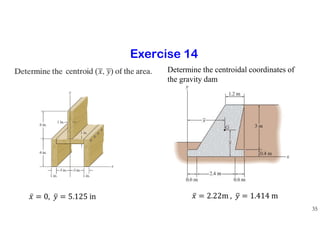
The document discusses the concepts of centroid and center of gravity. It provides examples of calculating the centroid of different plane areas using integration, including triangles, composite shapes, and areas with cutouts. The key steps shown are: 1) Setting up integrals with differential area elements to calculate x- and y-coordinates of the centroid 2) For composite shapes, treating each individual shape as a "part" and using a weighted average equation based on the area and centroid of each part 3) For shapes with cutouts, treating the cutout area as a "negative" part in the weighted average equation.

1. University of Engineering and Technology Peshawar, Pakistan
CE-117: Engineering Mechanics
MODULE 14:
Geometrical properties of Plane areas-I
(Area, Centroid)
1

2. Lecture Objectives
To discuss the concept of the centroid.
 To show how to determine the location of the centroid of an
area

3. Centre of Gravity:
It is defined as a point about which the entire weight of the body
is assumed to be concentrated.
It is related to distribution of mass.
Centroid
It is defined as a point about which the entire line, area or
volume is assumed to be concentrated.
It is related to distribution of length, area and volume.
3

4. 4

5. 5

6. 6

7. 7

8. 8

9. 9

10. 10
Centroids of Areas
 Where x & y are the coordinates of the
differential element of area dA
 The subscript A on the integral sign means the
integration is carried out over the entire area
 The centroid of the area is:

11. 11
Problem 14.1:Centroid of an Area by Integration
Determine the centroid of the
triangular area in Fig.
Strategy
Determine the coordinates of the centroid by using an element
of area dA in the form of a “strip” of width dx.
Fig

12. 12
Solution
Let dA be the vertical strip. The height of the
strip is (h/b)x, so dA = (h/b)x dx. To integrate
over the entire area, we must integrate with
respect to x from x = 0 to x = b. The x
coordinate of the centroid is:
b
x
b
h
x
b
h
dx
x
b
h
dx
x
b
h
x
dA
dA
x
x b
b
b
b
A
A
3
2
2
3
0
2
0
3
0
0


























Problem 14.1:Centroid of an Area by Integration

13. 13
Solution
To determine , we let y in Eq. (7) be the y
coordinate of the midpoint of the strip:
y
h
x
b
h
x
b
h
dx
x
b
h
dx
x
b
h
x
b
h
dA
dA
y
y b
b
b
b
A
A
3
1
2
3
2
1
2
1
0
2
0
3
2
0
0






































Problem 14.1:Centroid of an Area by Integration

14. 14
Solution
The centroid is shown:
Problem 14.1:Centroid of an Area by Integration

15. 15
Critical Thinking
 Always be alert for opportunities to check your results:
 In this example, we should make sure that our integration procedure
gives the correct result for the area of the triangle:
bh
x
b
h
dx
x
b
h
dA
b
b
A 2
1
2 0
2
0








 

Problem 14.1:Centroid of an Area by Integration

16. Determine the coordinates of the centroid of
the area that lies between the
straight line x = 2y/3 and the parabola x2 = 4y,
where x and y are measured in
inches—see Fig. (a).
Use the following methods:
1. single integration using a horizontal
differential area element; and
2. single integration using a vertical
differential area element.
16
Problem 14.2:Centroid of an Area by Integration

17. Part 1 Single Integration: Horizontal Differential
Area Element
The horizontal differential area element is shown
in Fig. (c).
17
Problem 14.2:Centroid of an Area by Integration

18. 18
3 in.
3.6
in.
Problem 14.2:Centroid of an Area by Integration

19. Part 2 Single Integration: Vertical Differential
Area Element
19
Problem 14.2:Centroid of an Area by Integration

20. 20
Problem 14.2:Centroid of an Area by Integration

21. 21
Centroids of Plane Areas

22. 22
Centroids of Plane Areas

23. 23
Centroids of Plane Areas

24. 24
Centroids of Areas
 Keeping in mind that the centroid of an area is its average position
will often help you locate it:
 E.g. the centroid of a circular area or a rectangular area obviously lies
at the center of the area
 If an area has “mirror image” symmetry about an axis, the centroid
lies on the axis
 If an area is symmetric about 2 axes, the centroid lies at their
intersection

25. 25
Centroids of Composite Areas
 Composite area: an area consisting of a combination of simple
areas
 The centroid of a composite area can be determined without
integration if the centroids of its parts are known
 The area in the figure consists of a
triangle, a rectangle & a semicircle,
which we call parts 1, 2 & 3

26. 26
Centroids of Composite Areas
 The x coordinate of the centroid of the composite area is:
(1)
 From the equation for the x coordinate of the centroid of part 1:
 We obtain:














3
2
1
3
2
1
A
A
A
A
A
A
A
A
dA
dA
dA
dA
x
dA
x
dA
x
dA
dA
x
x



1
1
1
A
A
dA
dA
x
x
1
1
1
A
x
dA
x
A



27. 27
Centroids of Composite Areas
 Using this equation & equivalent equations for parts 2 & 3, we can
write Eq. (1) as:
 The coordinates of the centroid of a composite area with an arbitrary
number of parts are:
(2)
3
2
1
3
3
2
2
1
1
A
A
A
A
x
A
x
A
x
x





i
i
i
i
i
i
i
i
i
i
A
A
y
y
A
A
x
x





 ,

28. 28
Centroids of Composite Areas
 The area in the figure consists of triangular
area with a circular hole or cutout:
 Designate the triangular area (without the
cutout) as part 1 of the composite area & the
area of the cutout as part 2

29. 29
Centroids of Composite Areas
 The x coordinate of the centroid of the composite area is:
 Therefore, we can use Eqs.2 to determine the centroids of composite
areas containing cut outs by treating the cut outs as negative areas
2
1
2
2
1
1
2
1
2
1
A
A
A
x
A
x
dA
dA
dA
x
dA
x
x
A
A
A
A











30. 30
Prob 14.1:Centroids of Composite Areas
Using the method of composite areas,
determine the location of the centroid of
the shaded area shown in Fig. (a).

31. 31
The area can be viewed as a rectangle, from which a semicircle and a
triangle have been removed.
+ - -
Prob 14.1:Centroids of Composite Areas

32. 32
+ - -
Prob 14.1:Centroids of Composite Areas

33. 33
Critical Thinking
 Although the area in this example may appear very artificial, many
of the areas dealt with in engineering applications consist of
combinations of simple areas such as these
 Even when that is not the case, an area can be approximated by
combining these kinds of simple areas
Prob 14.1:Centroids of Composite Areas

34. Exercise 14
34

35. 35
Exercise 14
Determine the centroidal coordinates of
the gravity dam