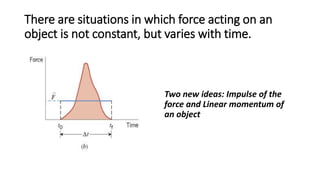
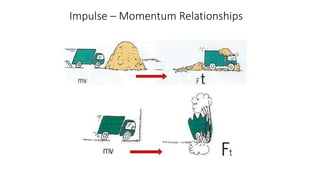
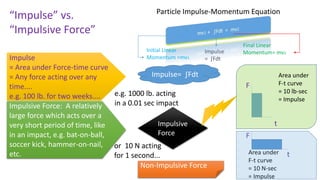
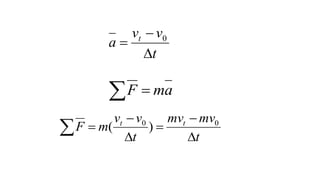1) The document discusses impulse and momentum. It defines impulse as the product of the average force and the time interval during which the force acts. Impulse is measured in newton-seconds (Ns).
2) Linear momentum is defined as the product of an object's mass and velocity. It is a vector quantity measured in kilogram-meters/second (kg m/s).
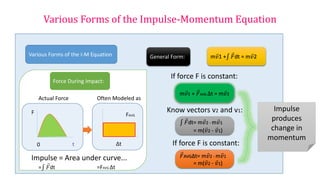
3) The Impulse-Momentum Theorem states that when a net force acts on an object, the impulse of the force is equal to the change in the object's momentum.