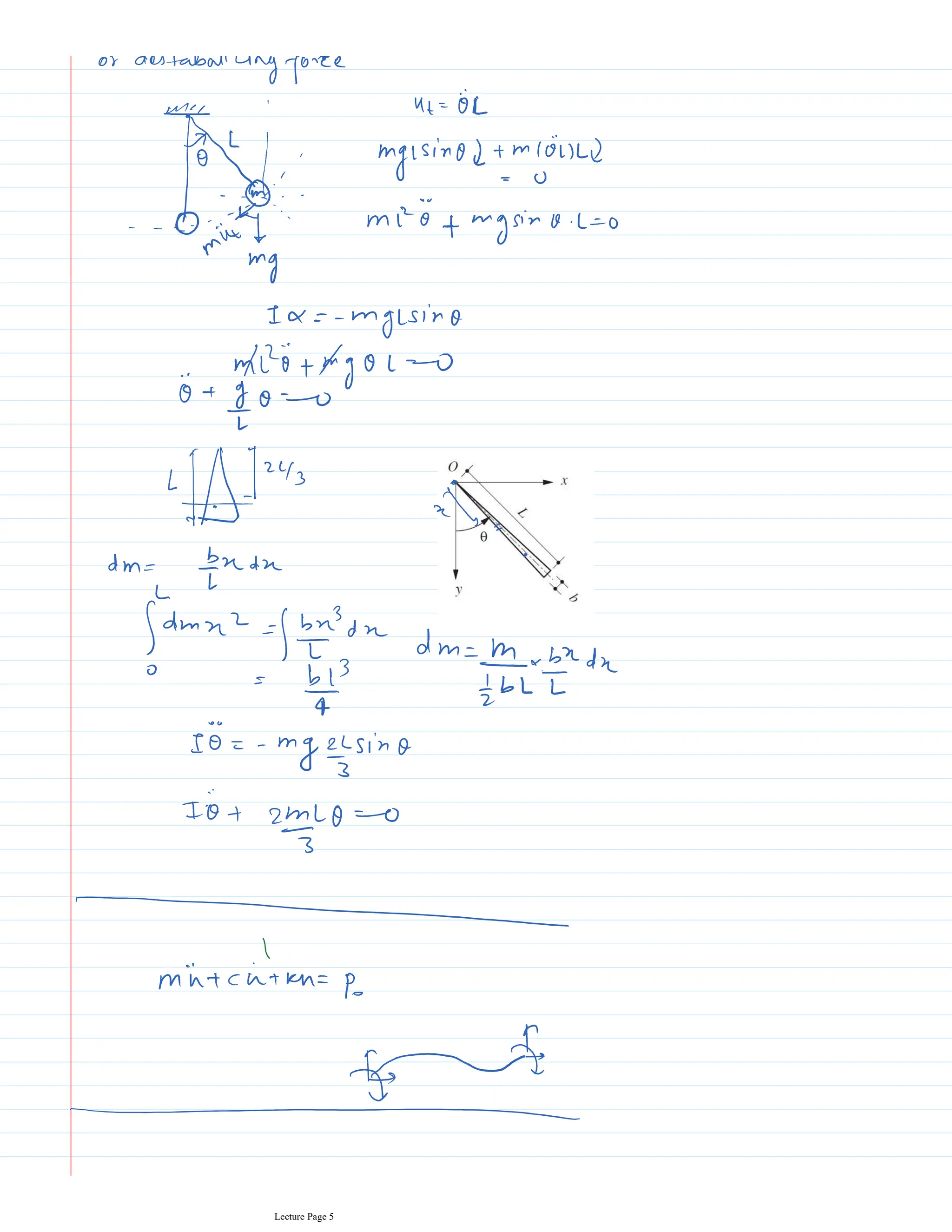
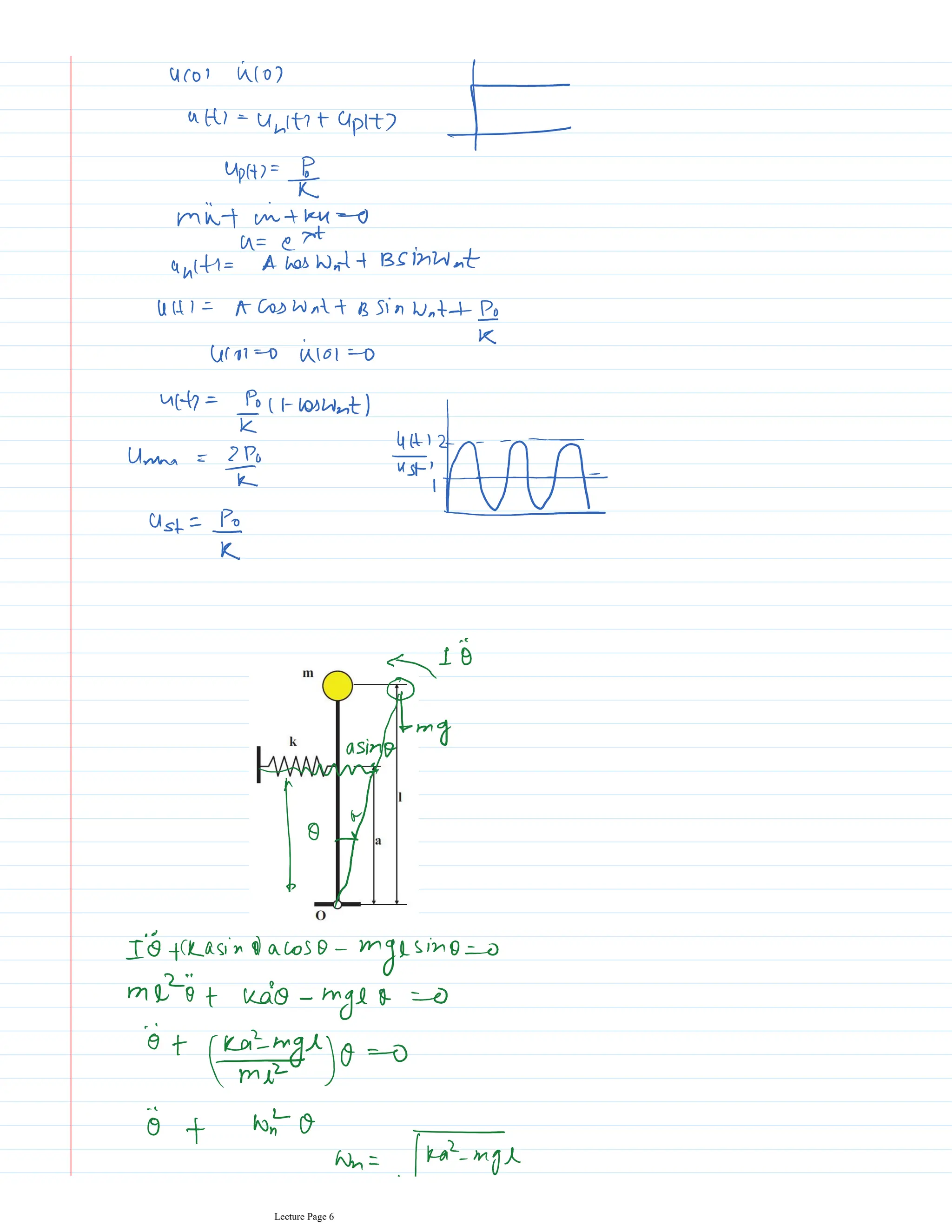
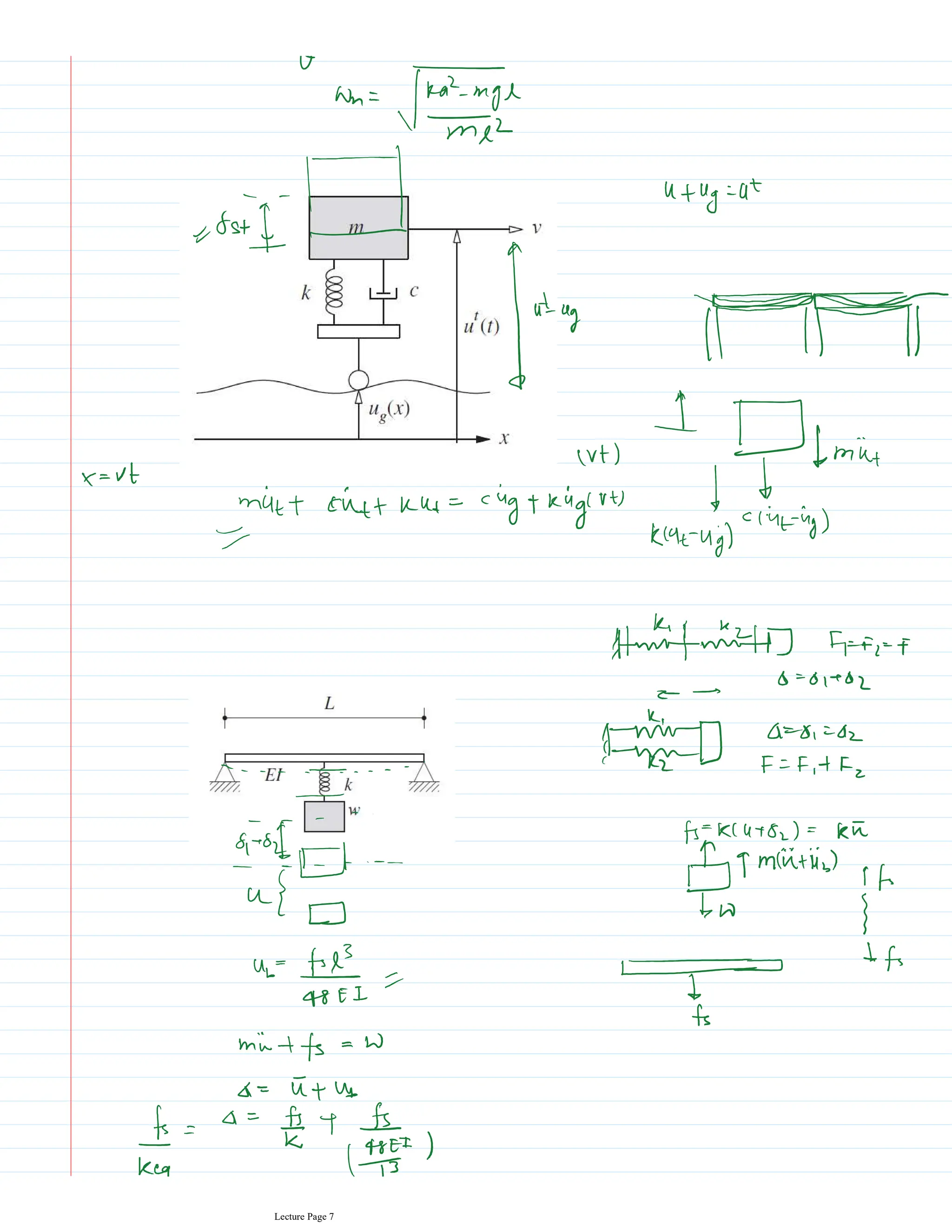
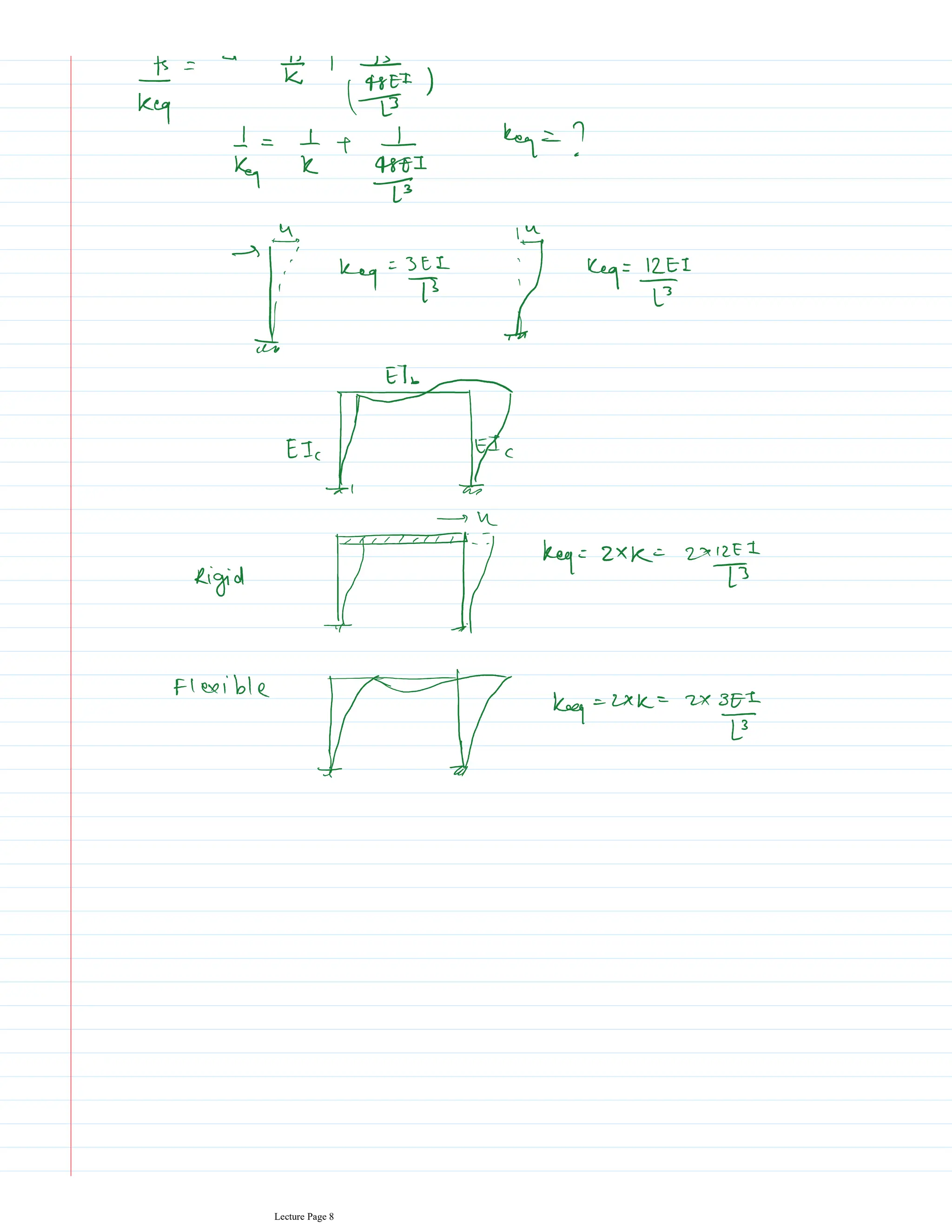
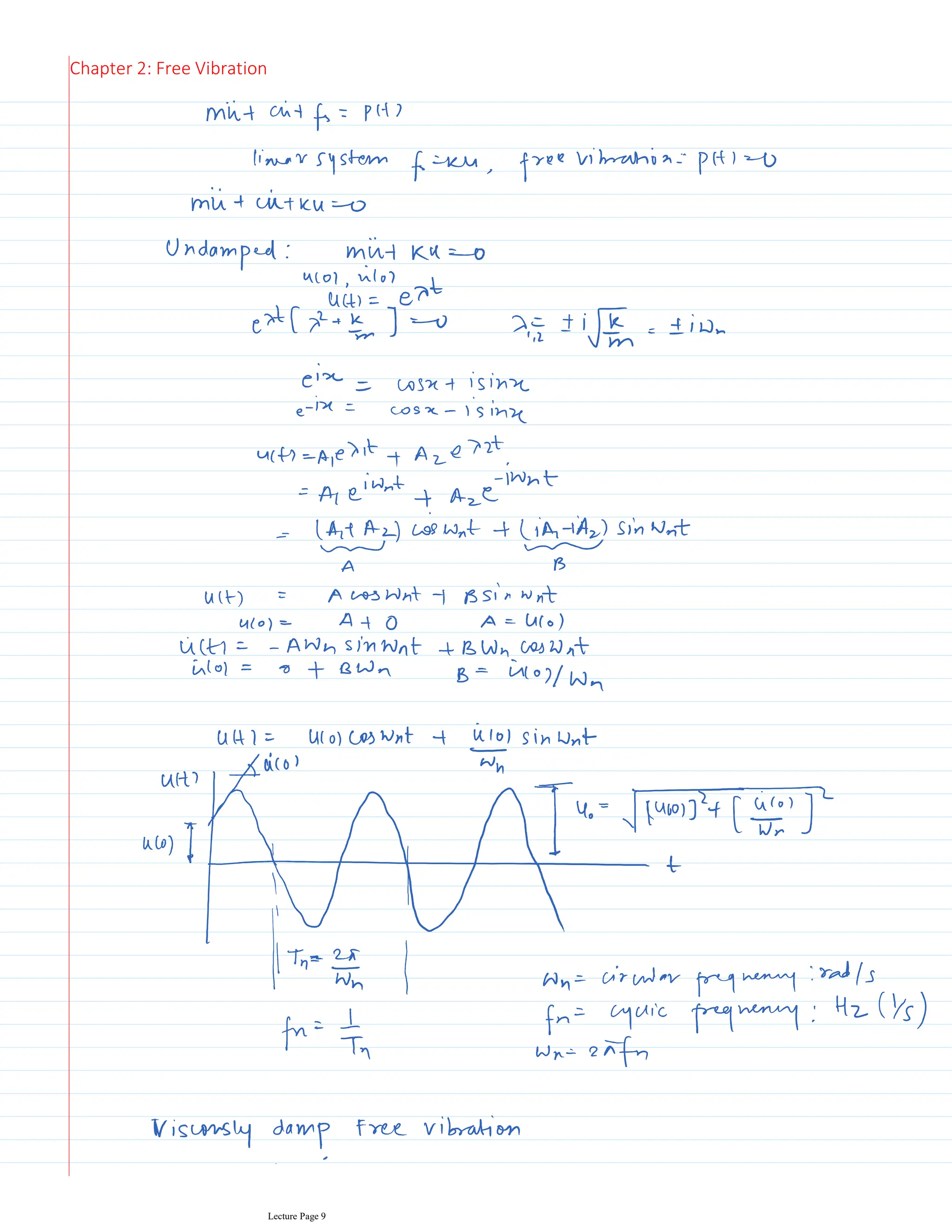
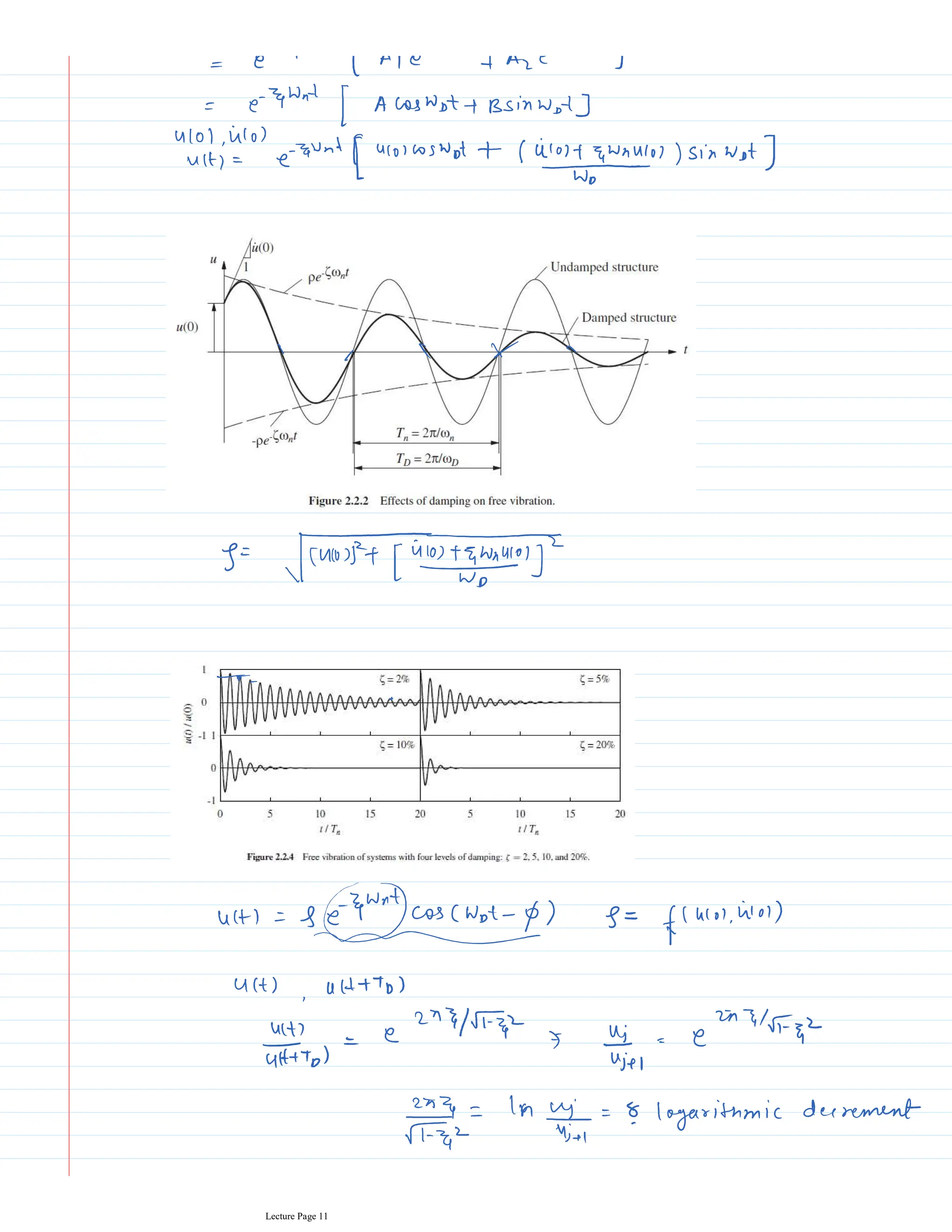
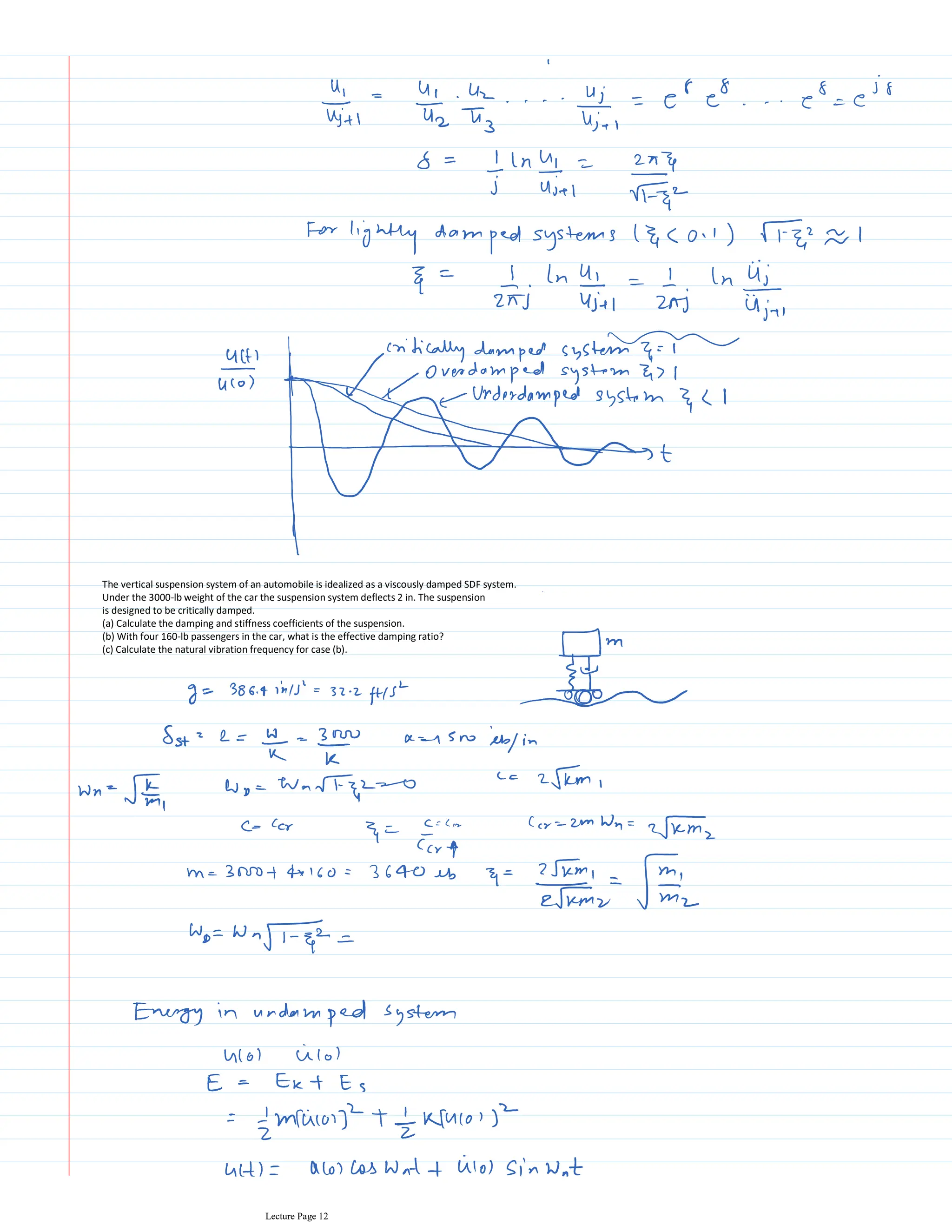
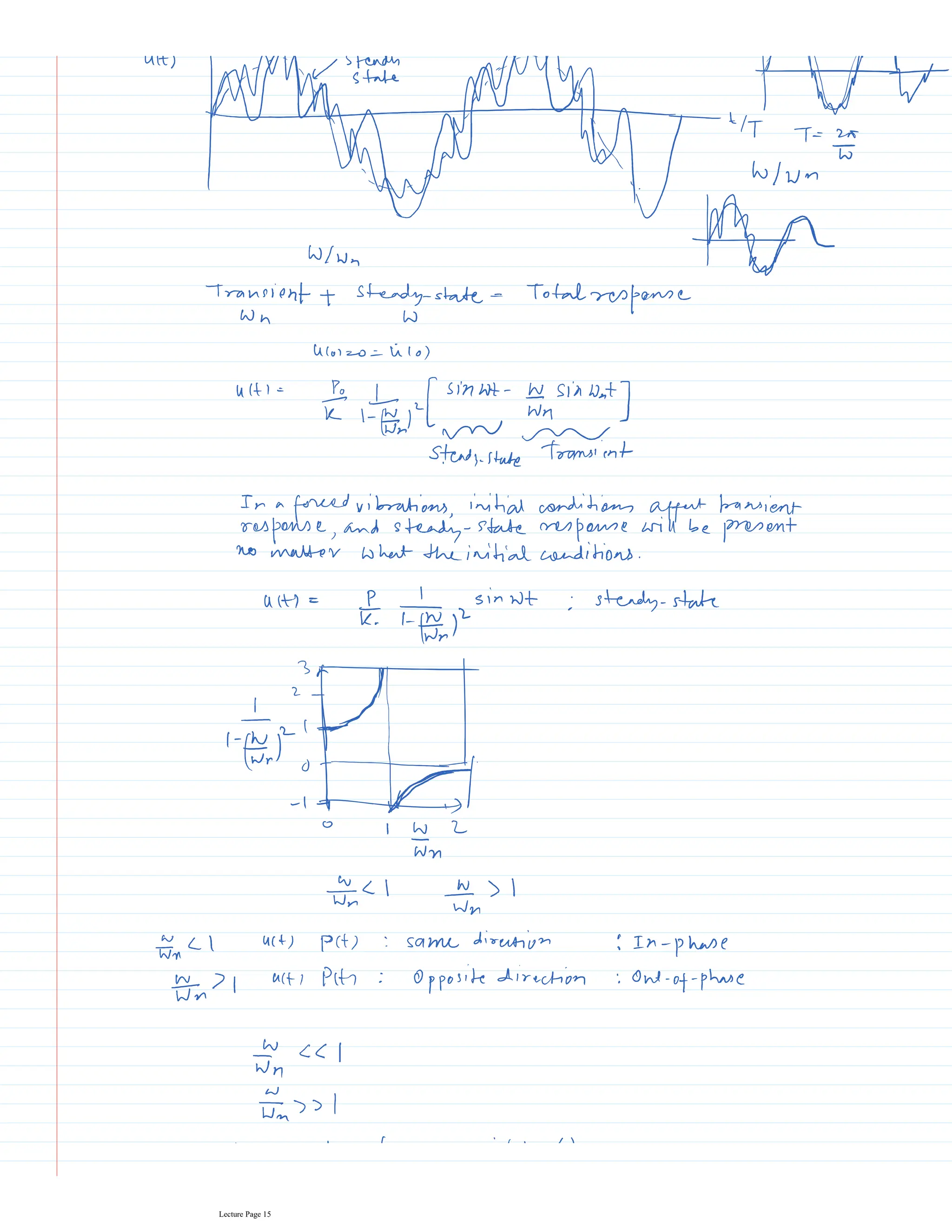
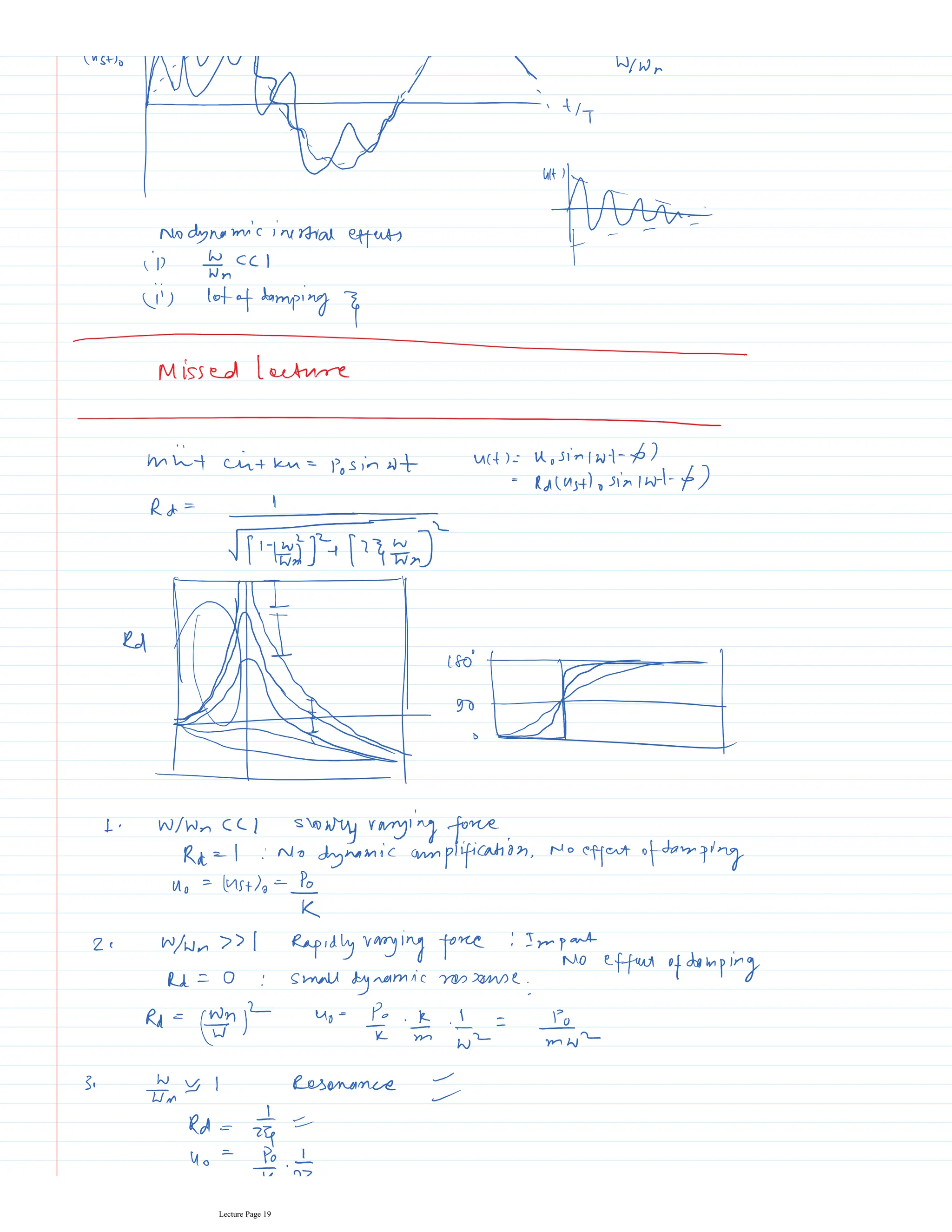
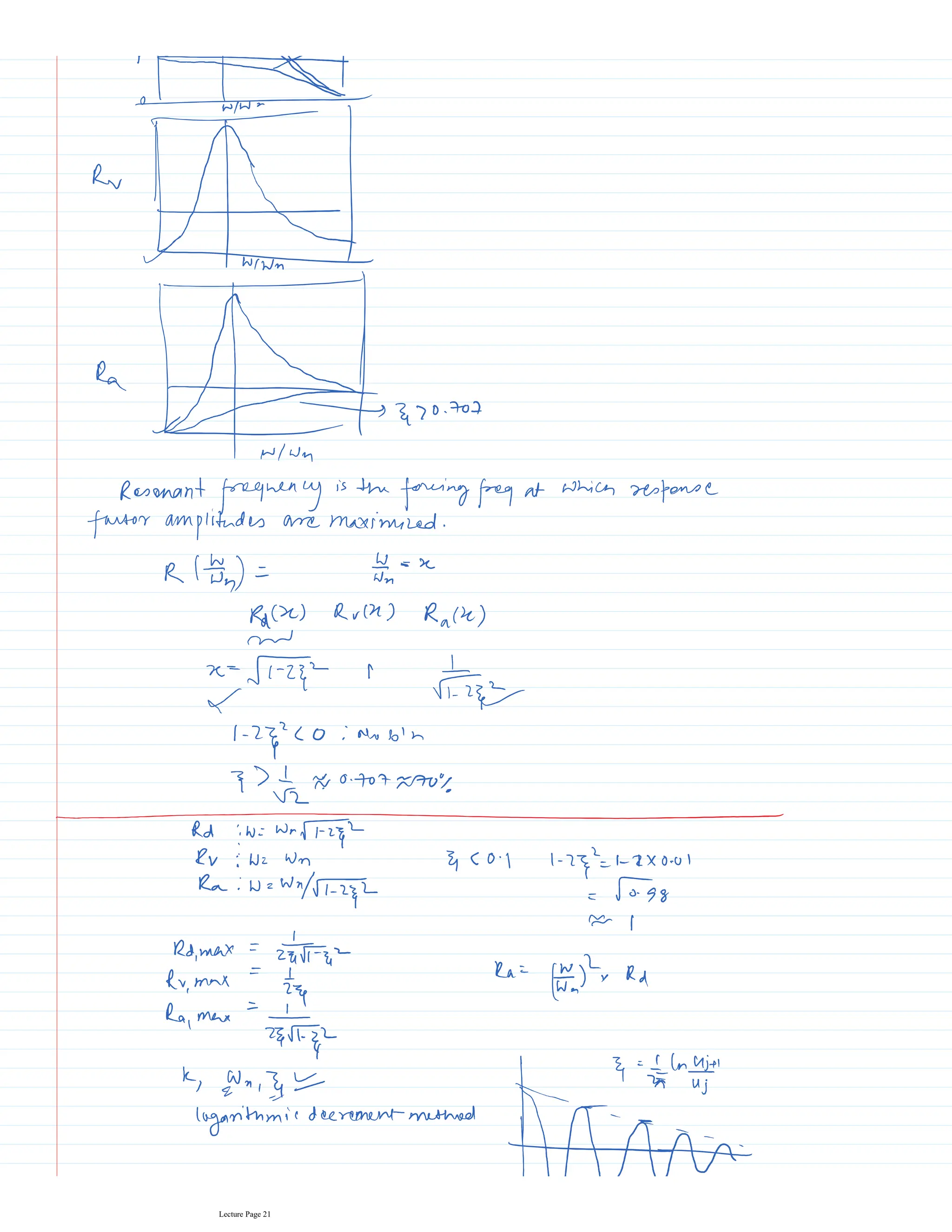
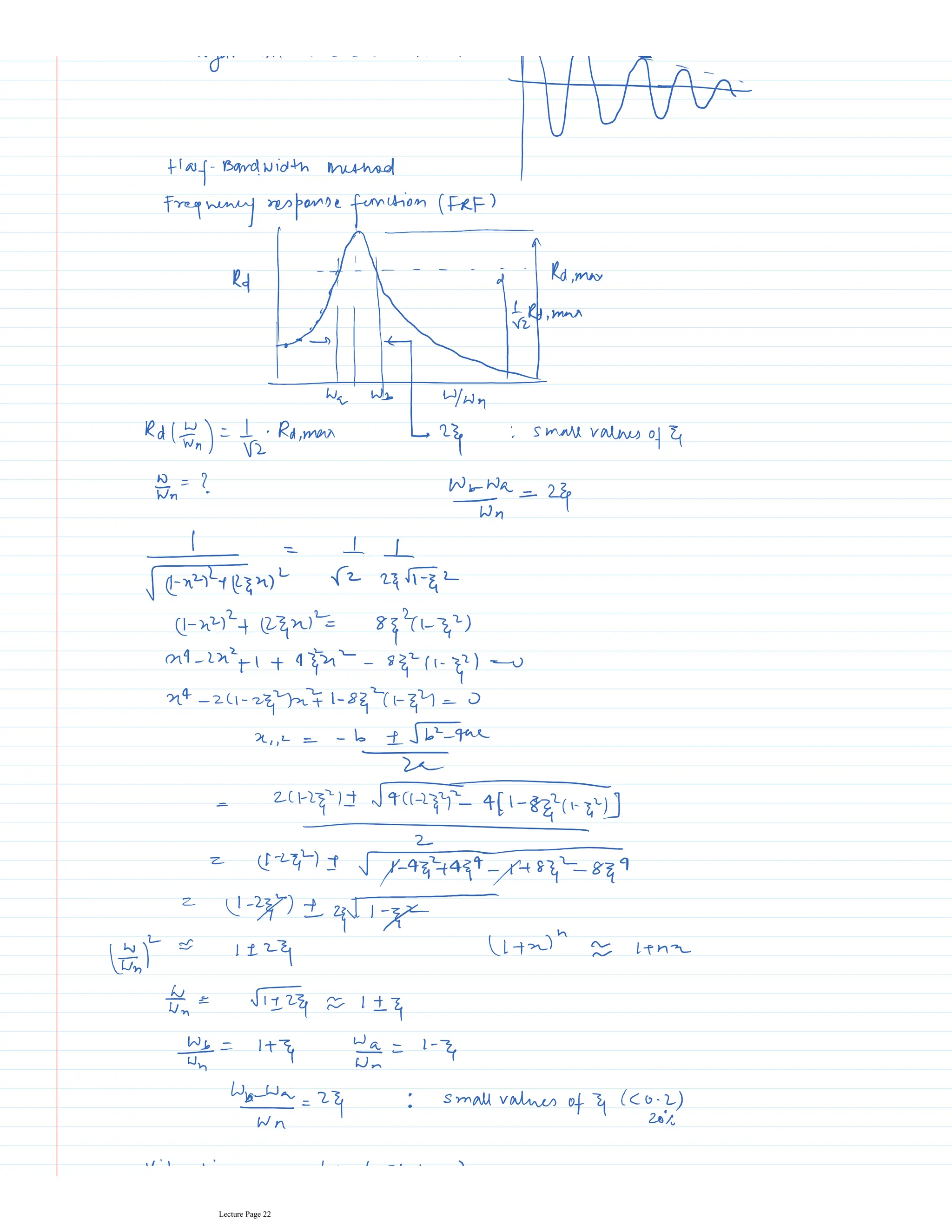
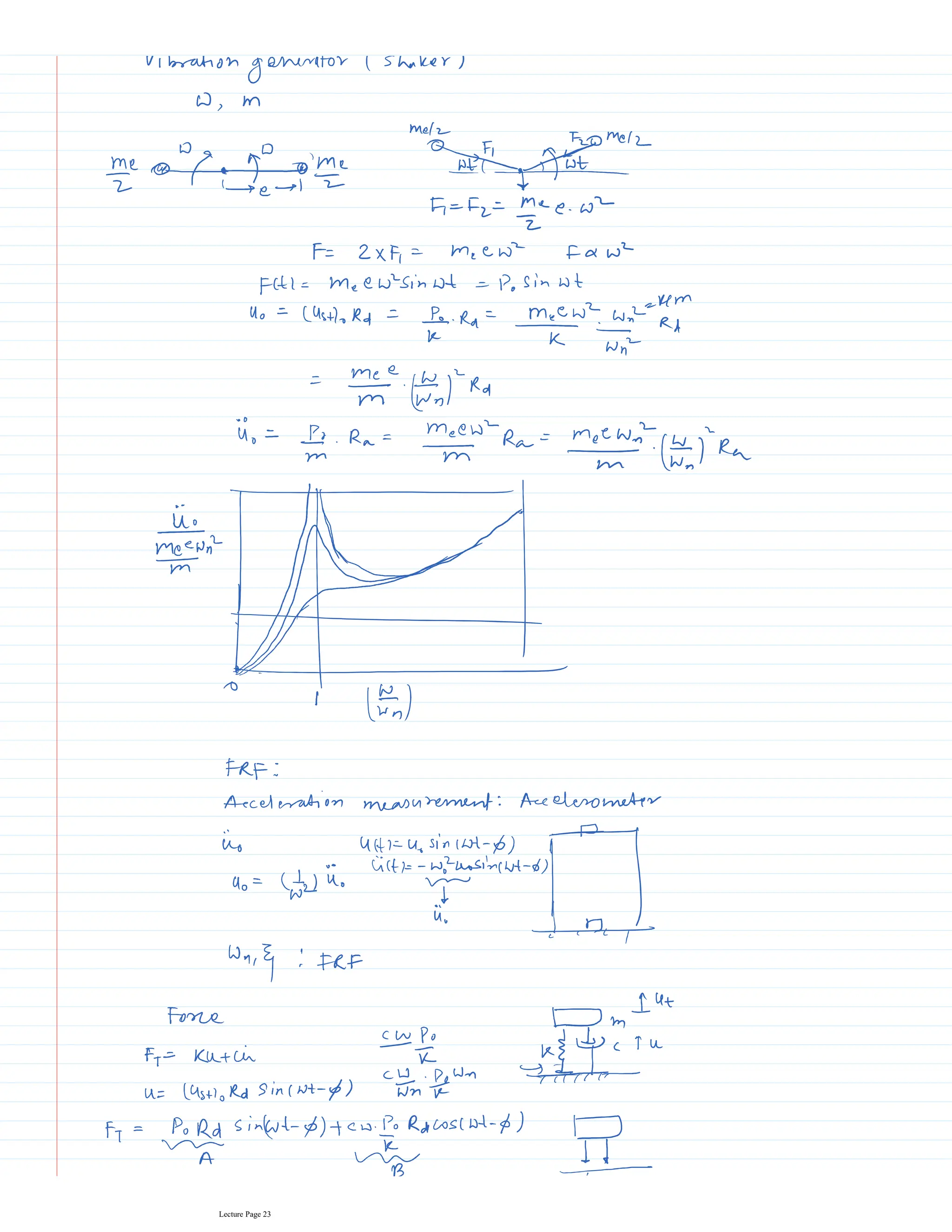
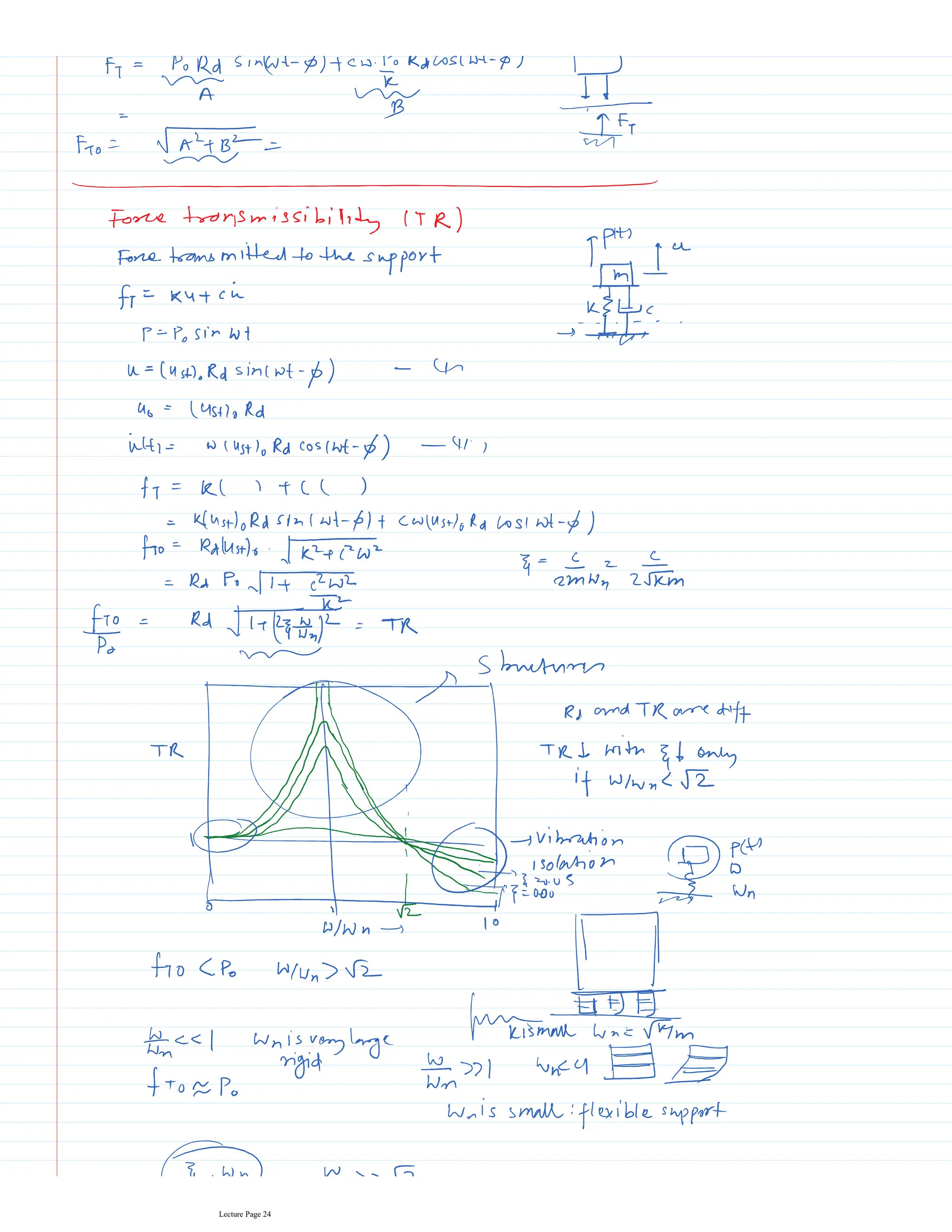
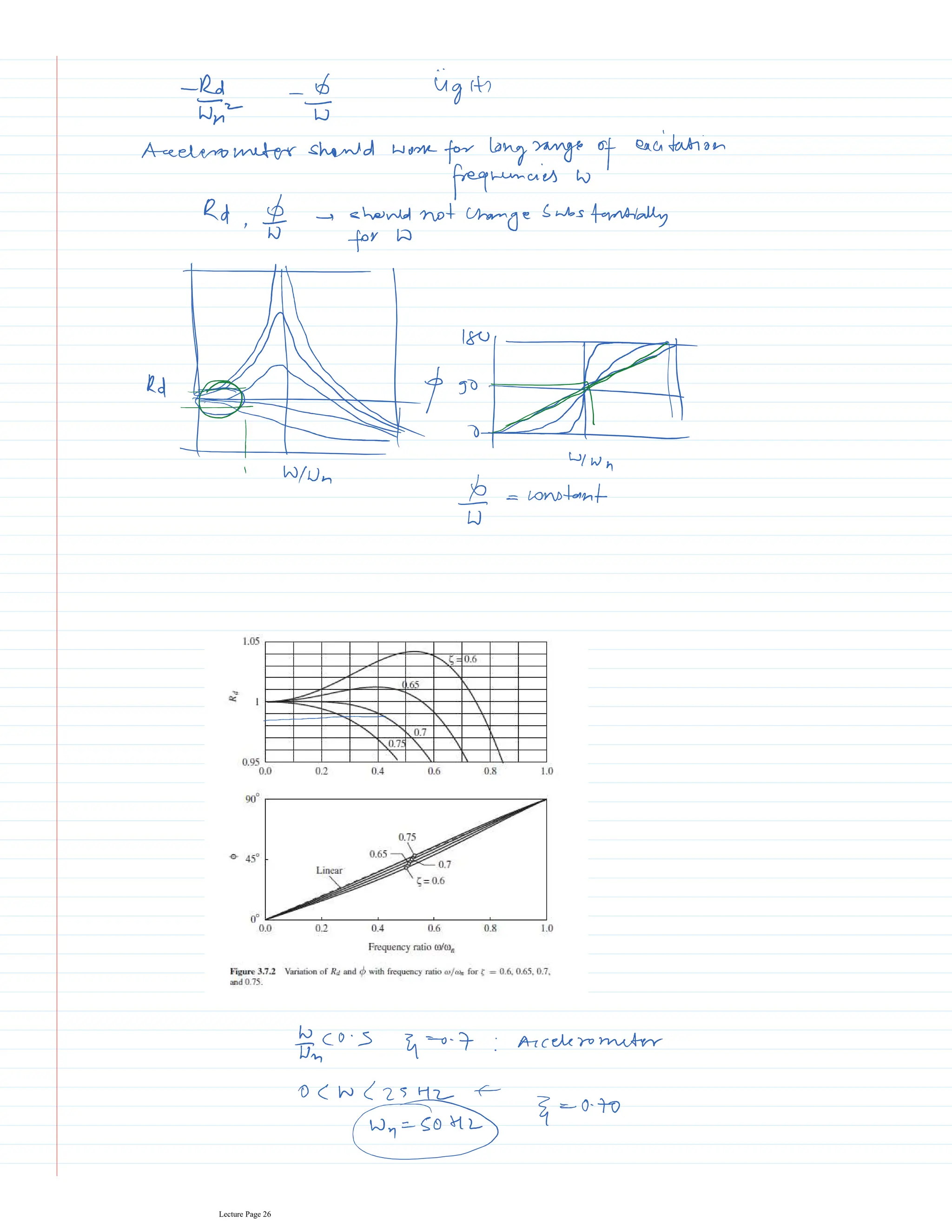
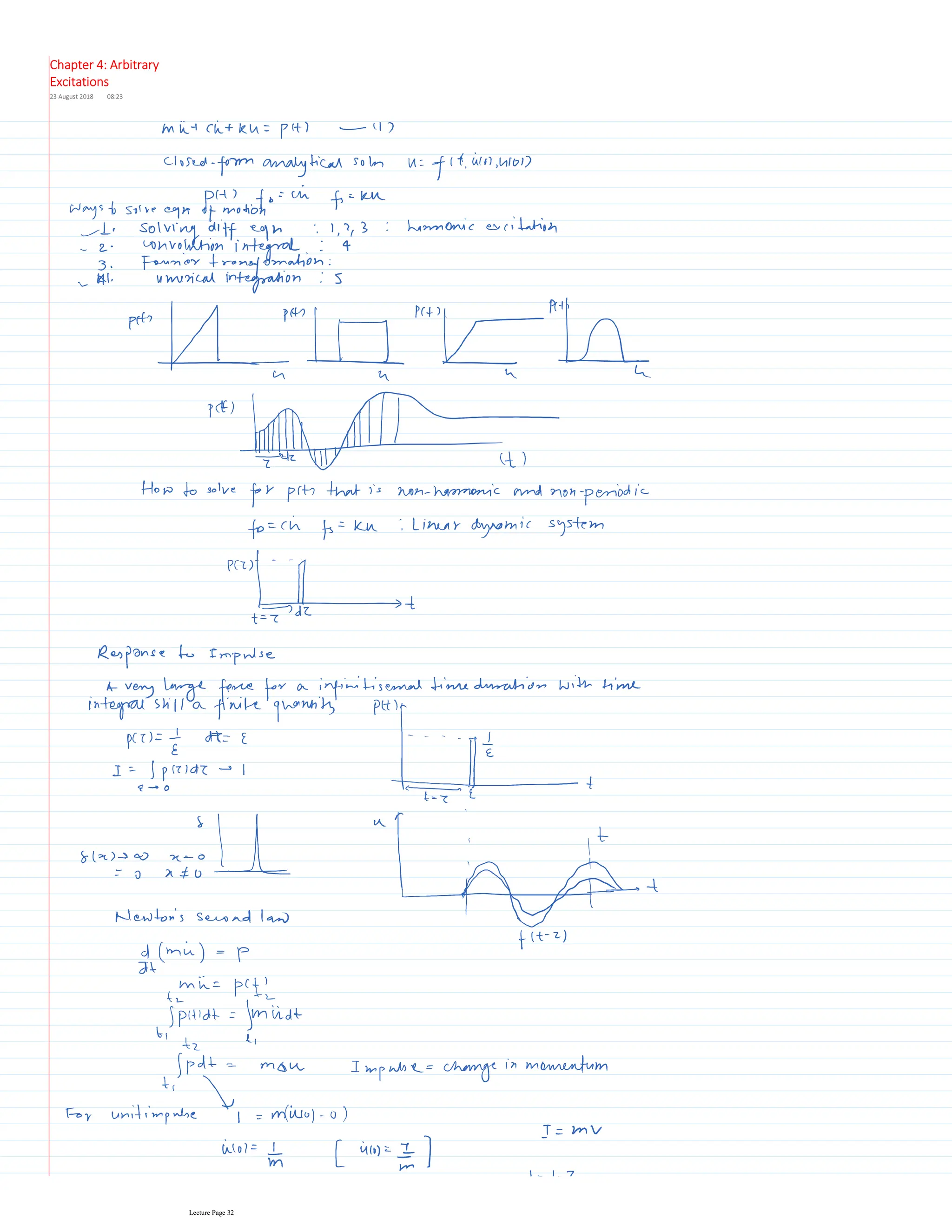
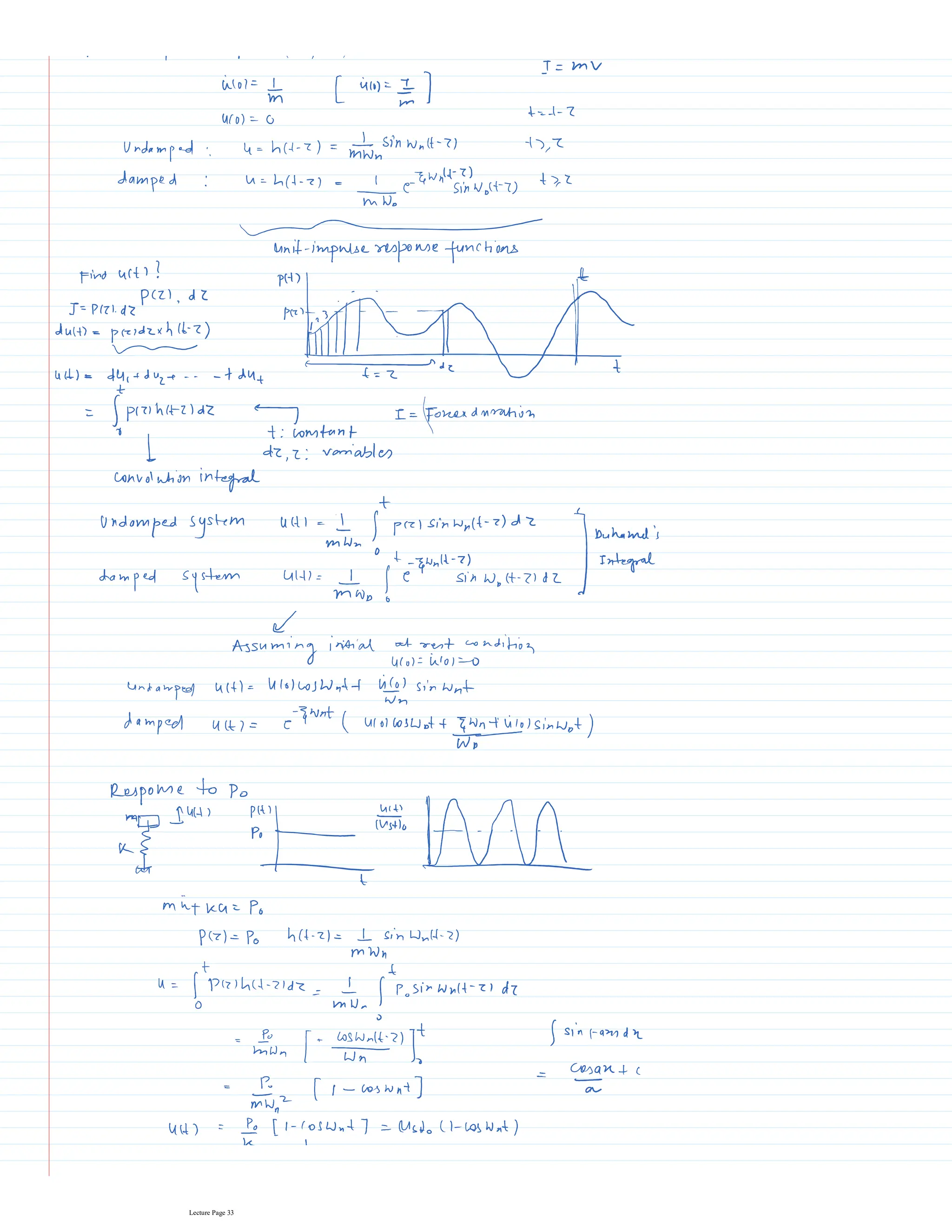
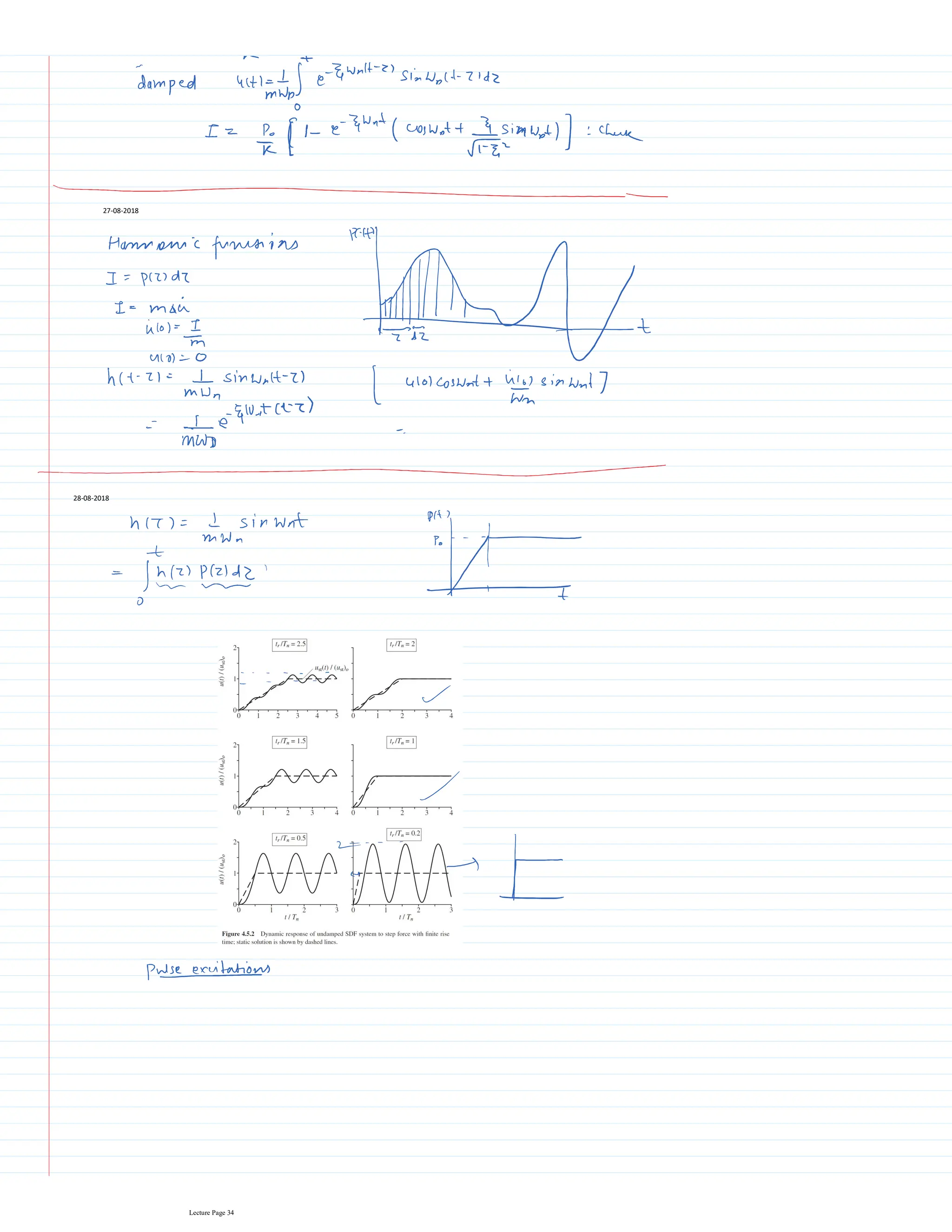
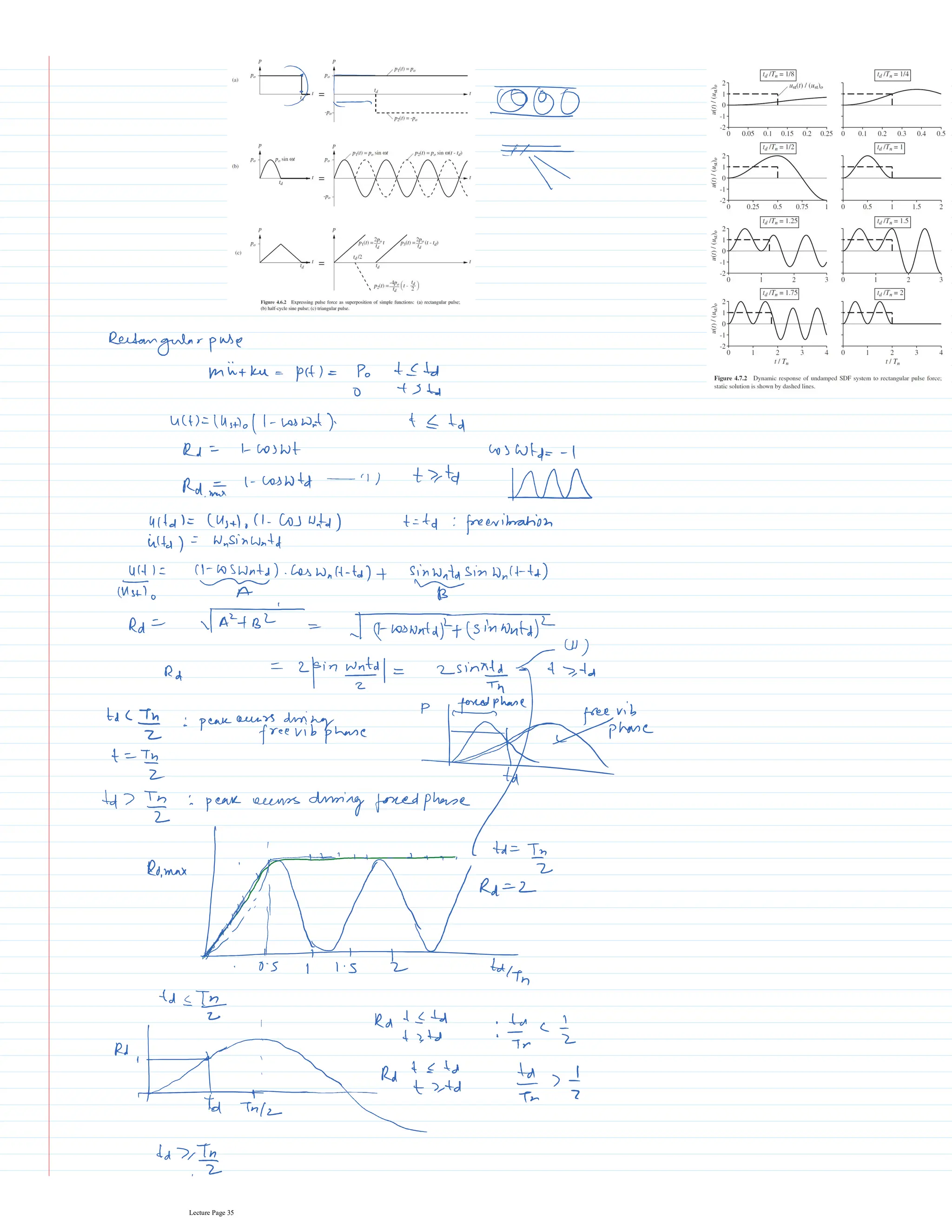
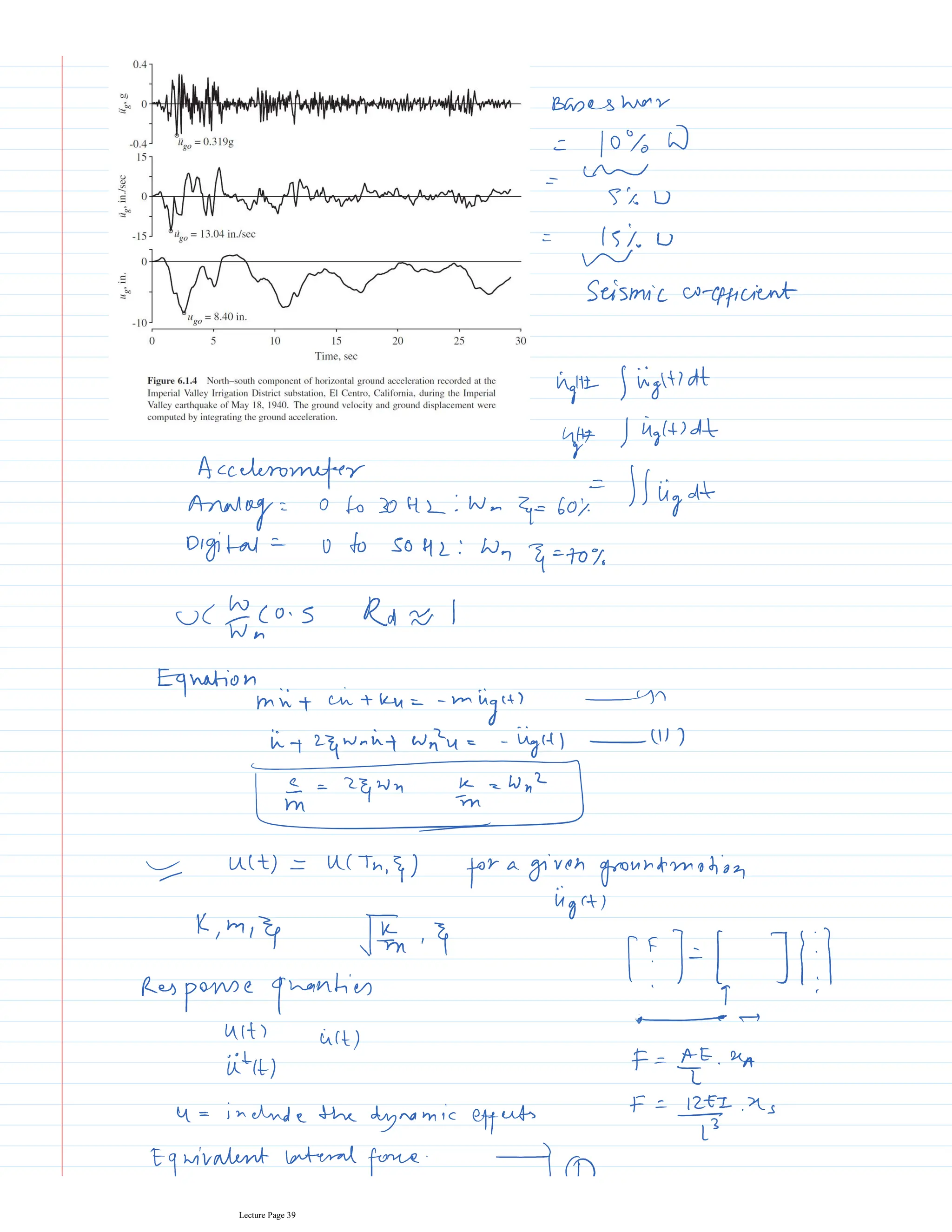
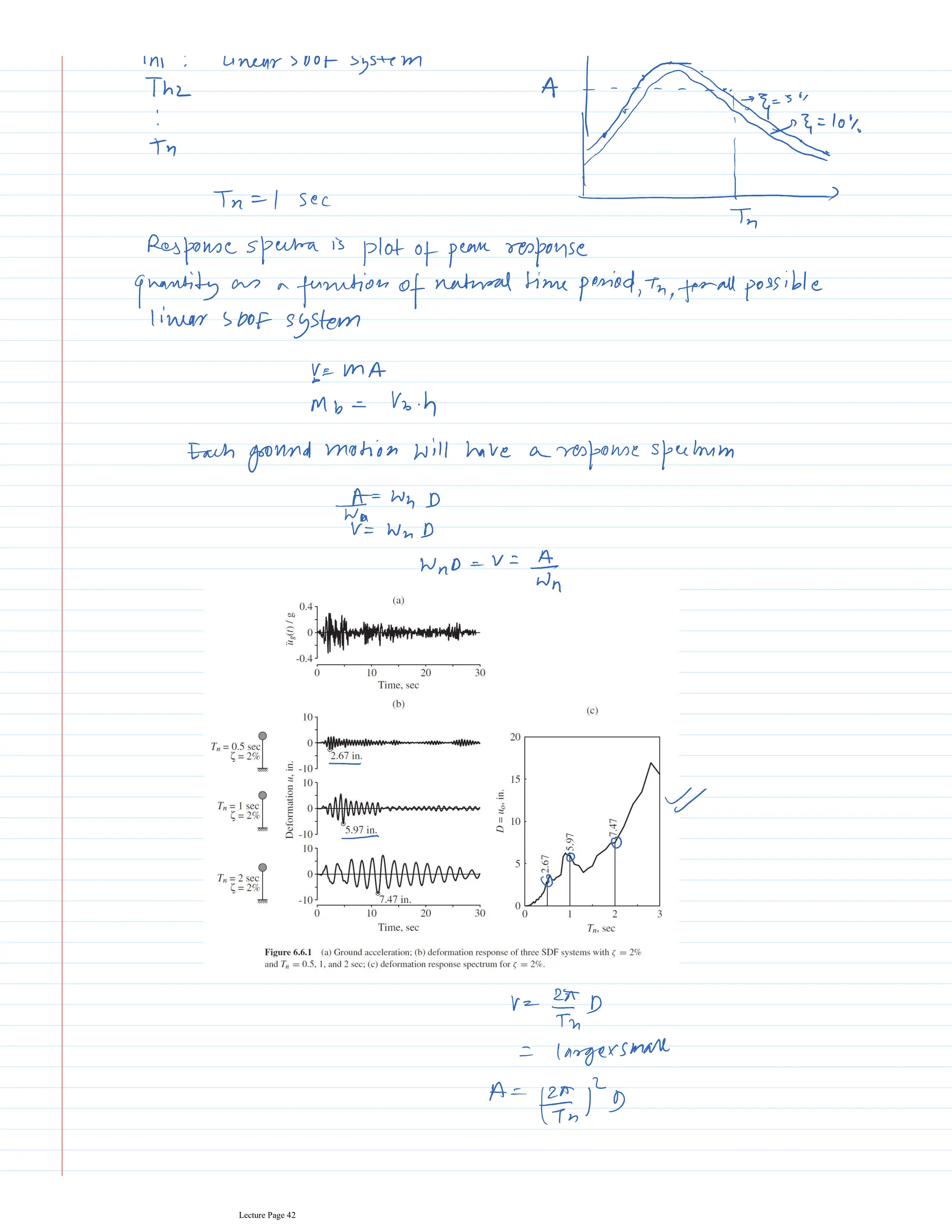
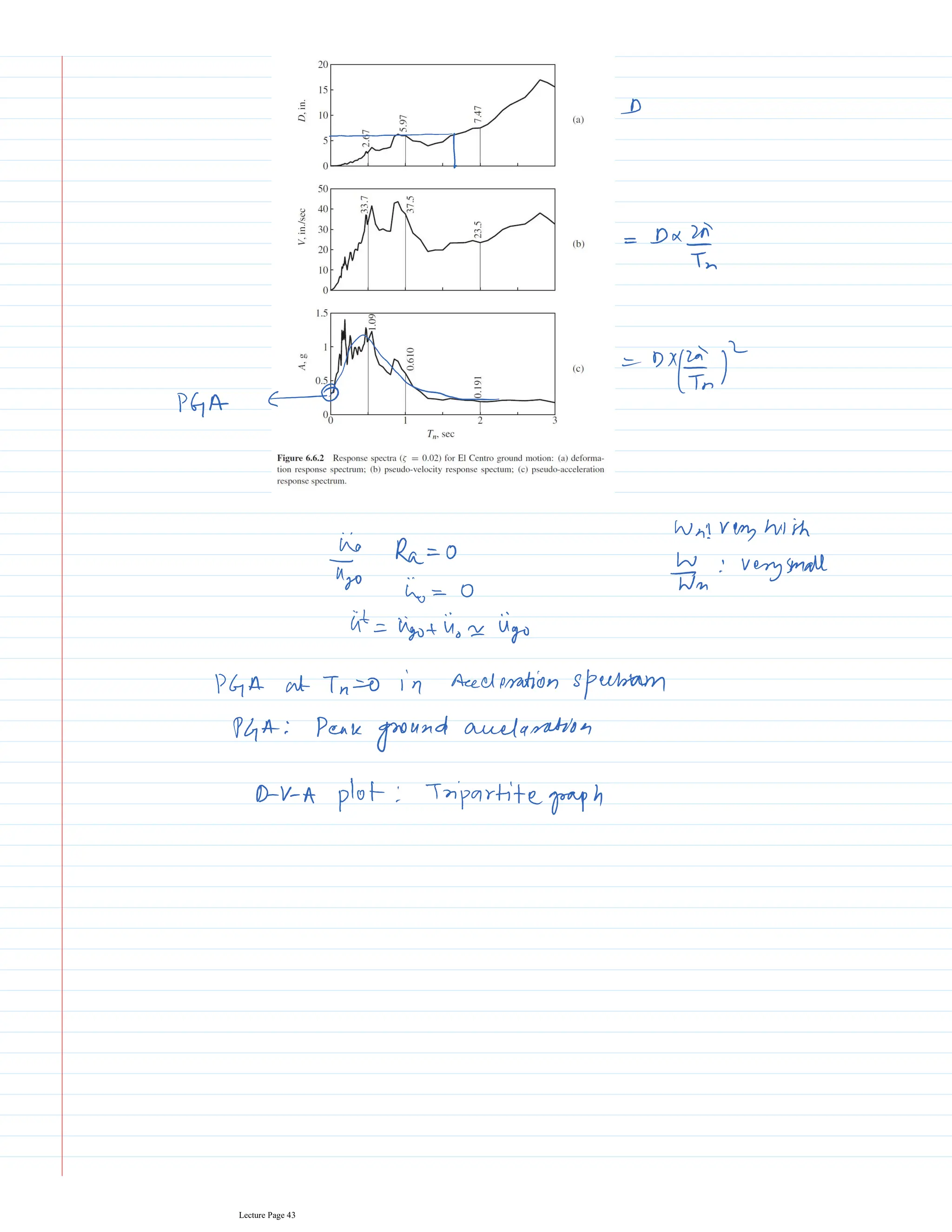
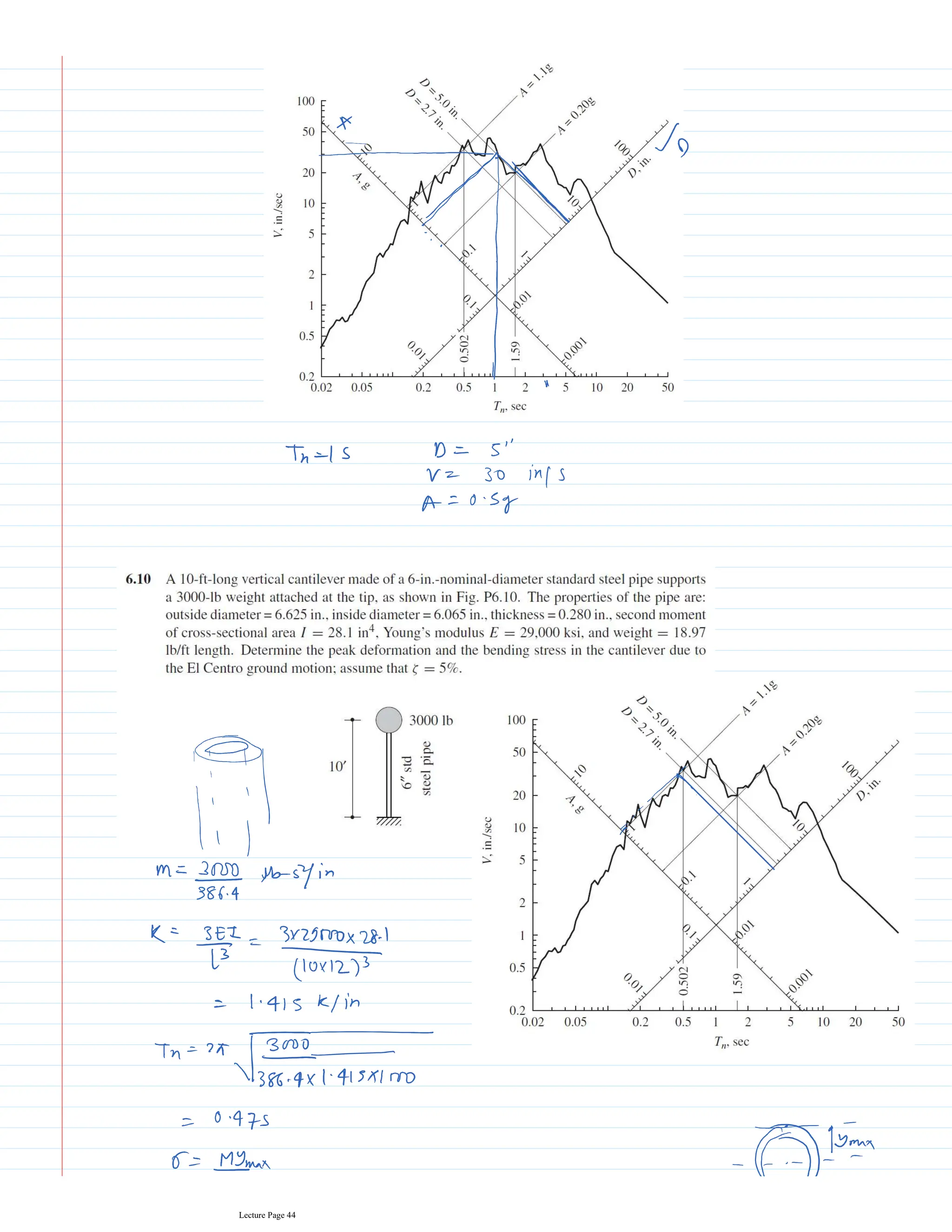
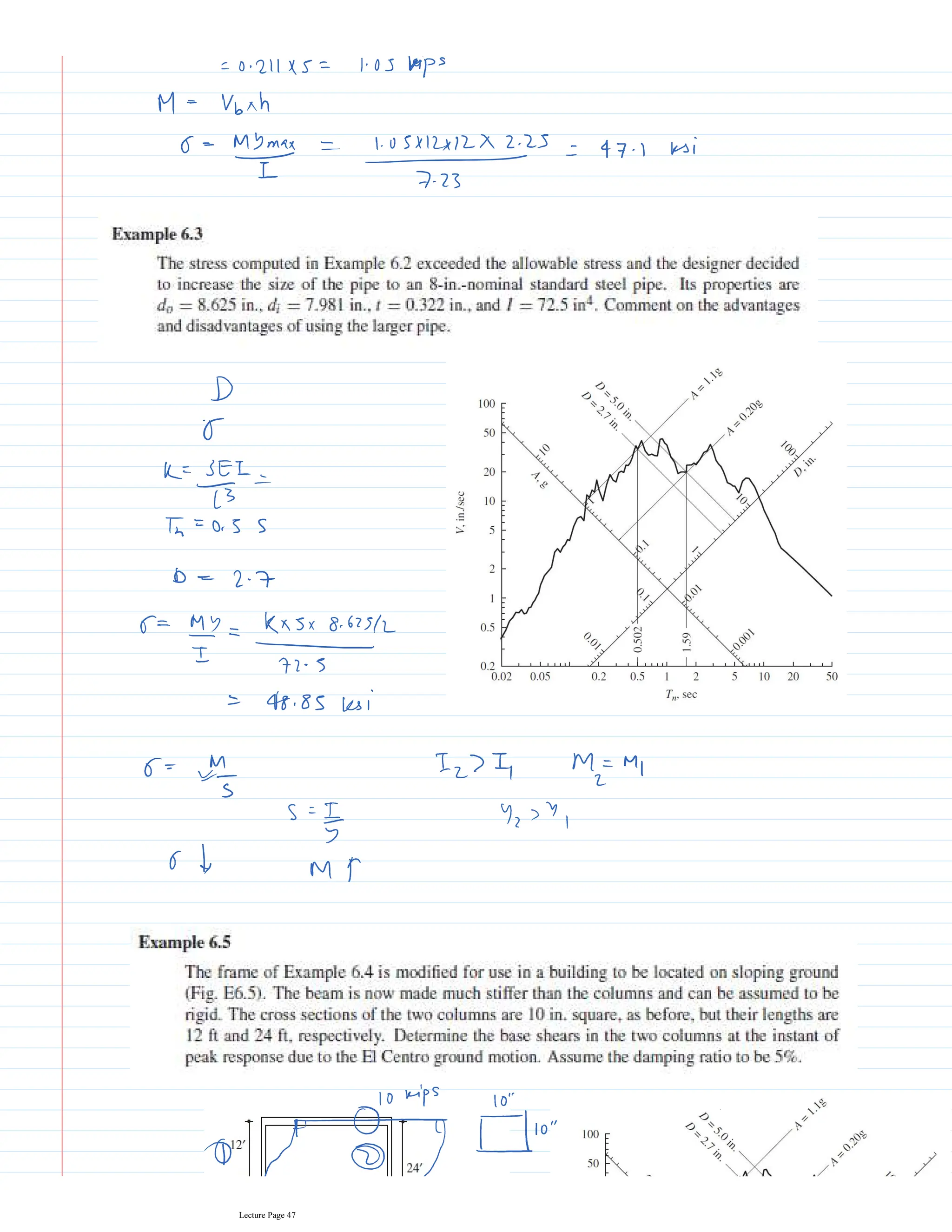
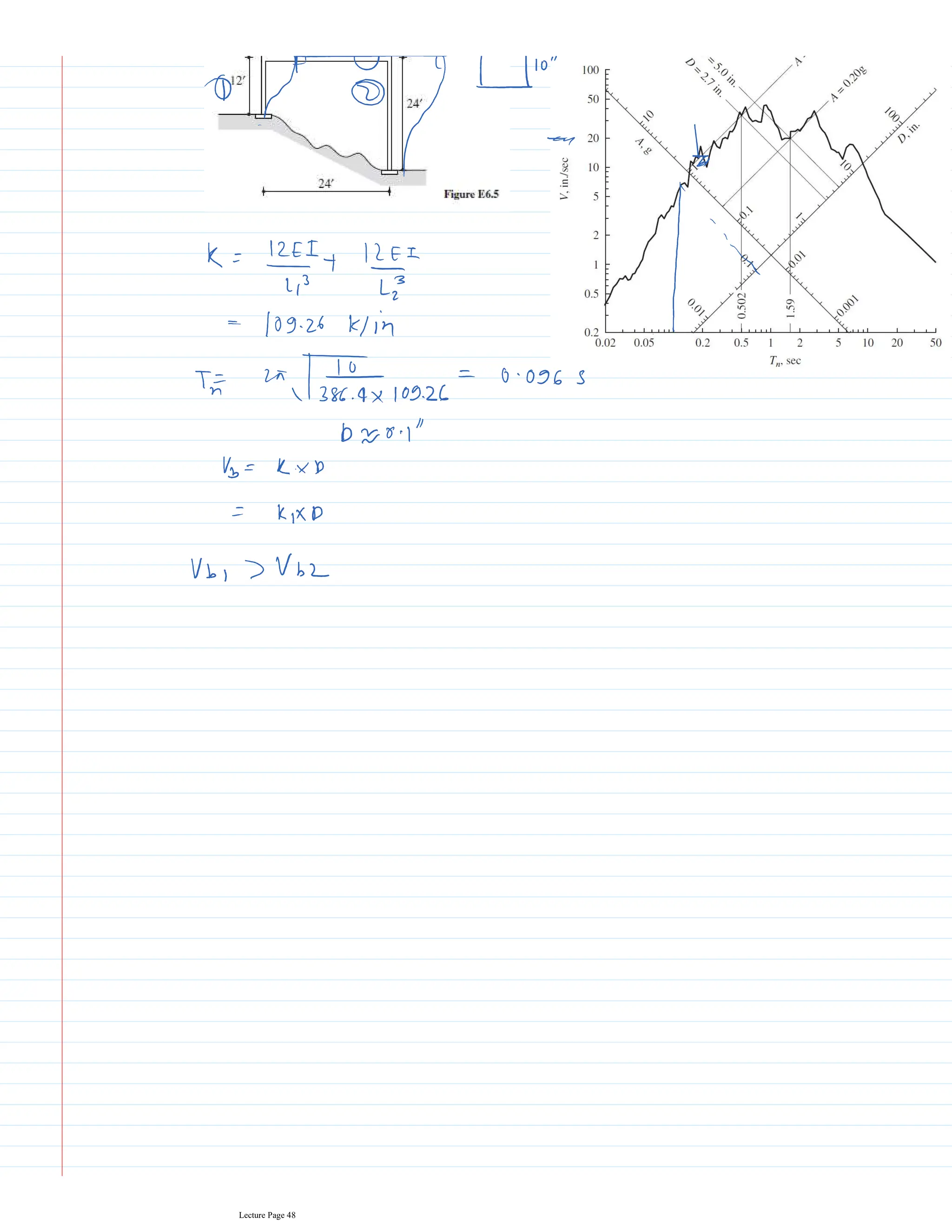
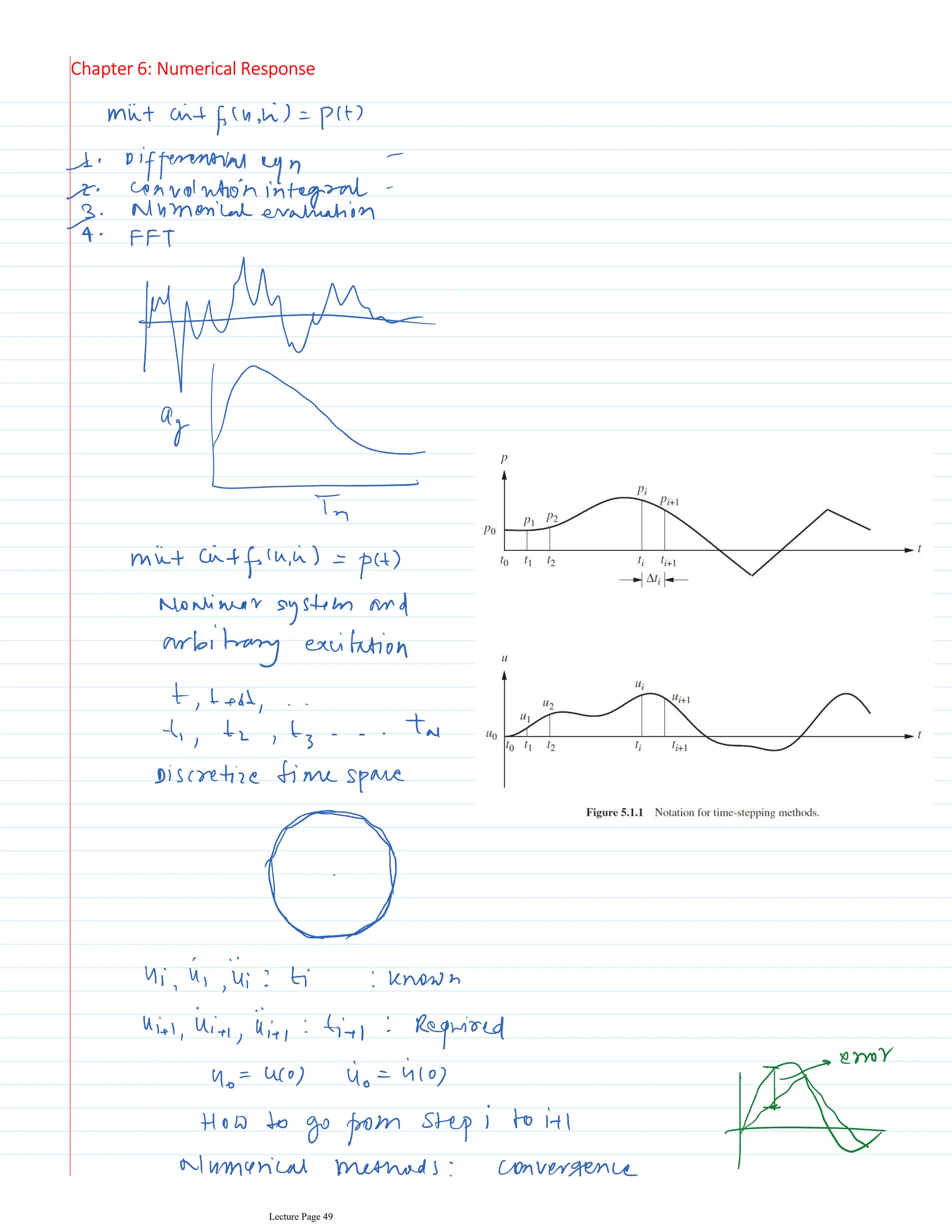
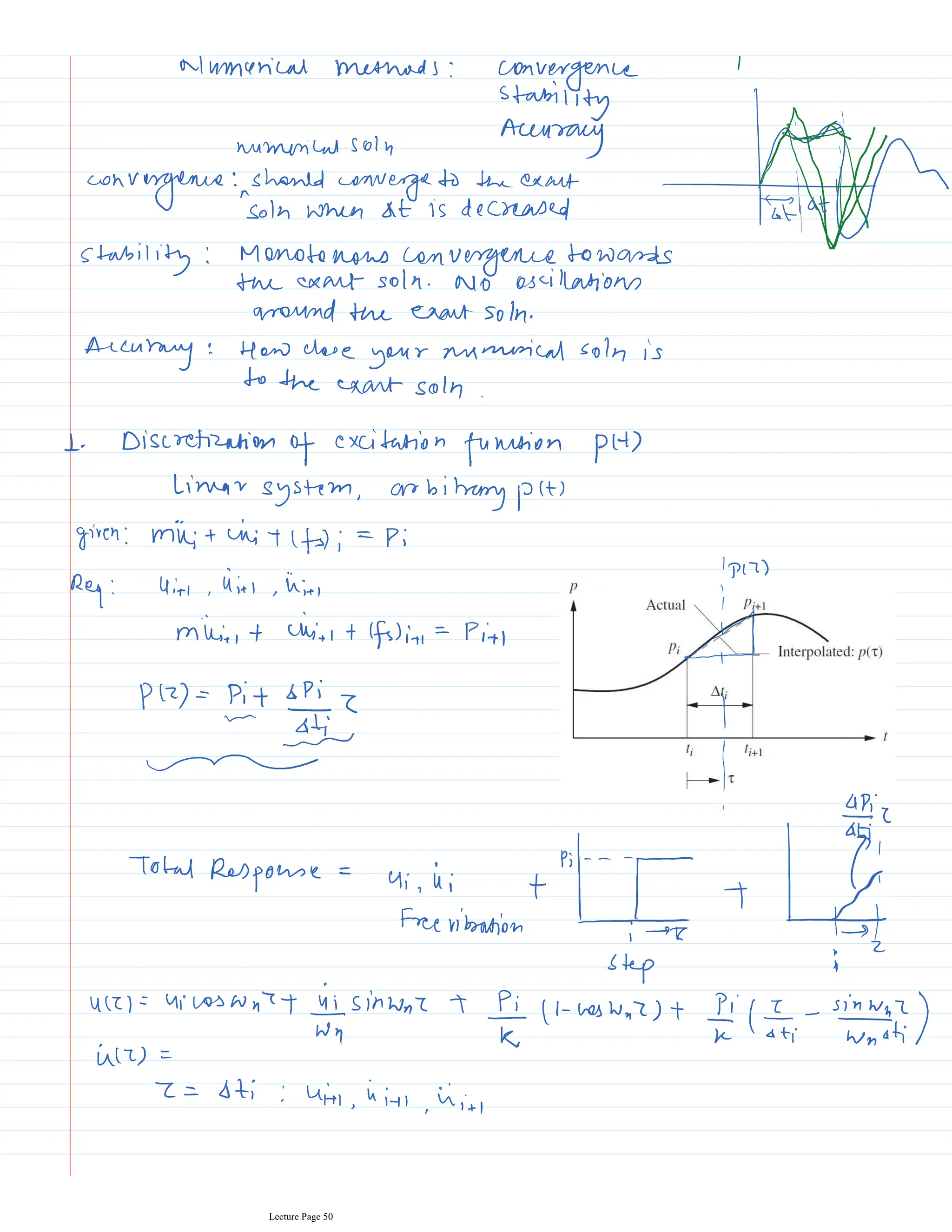
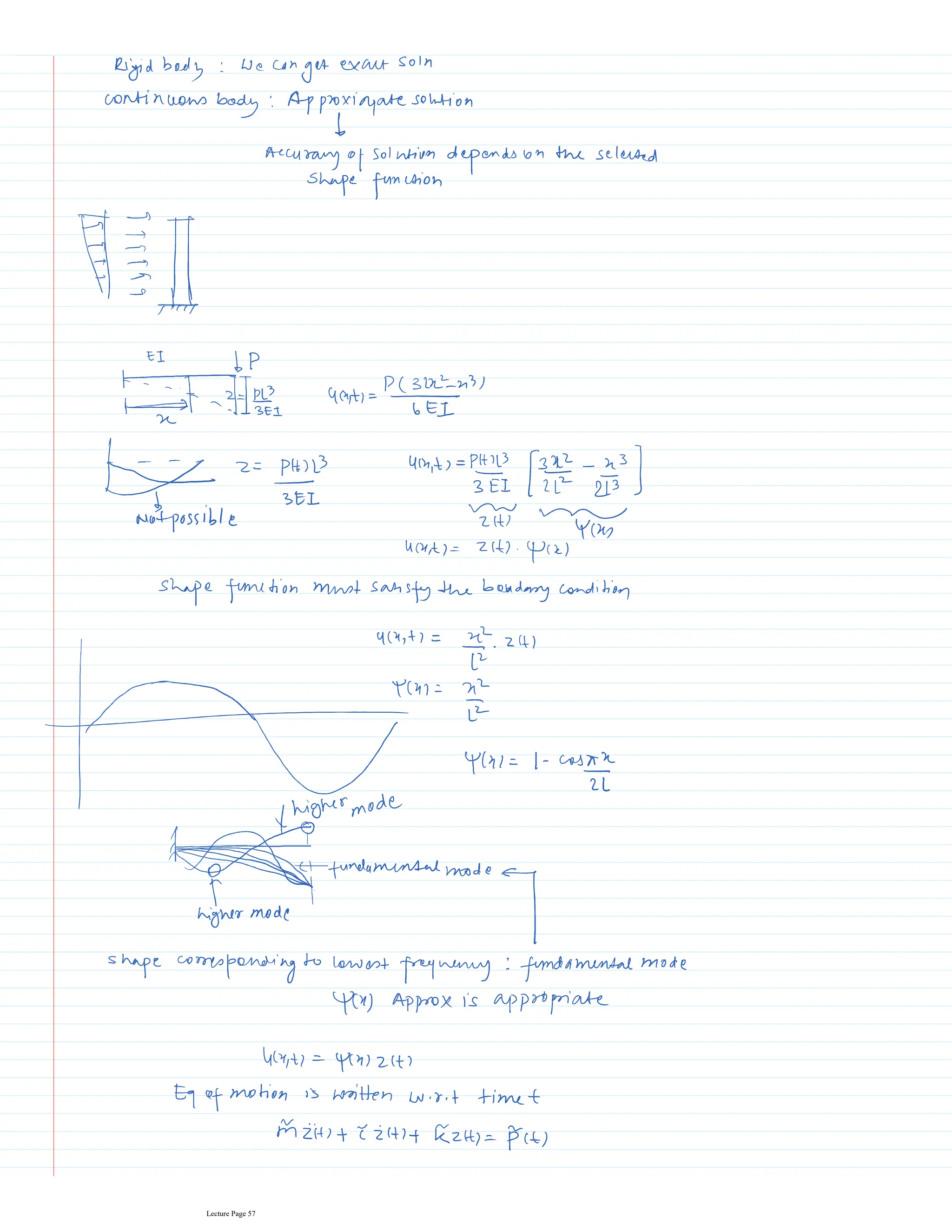
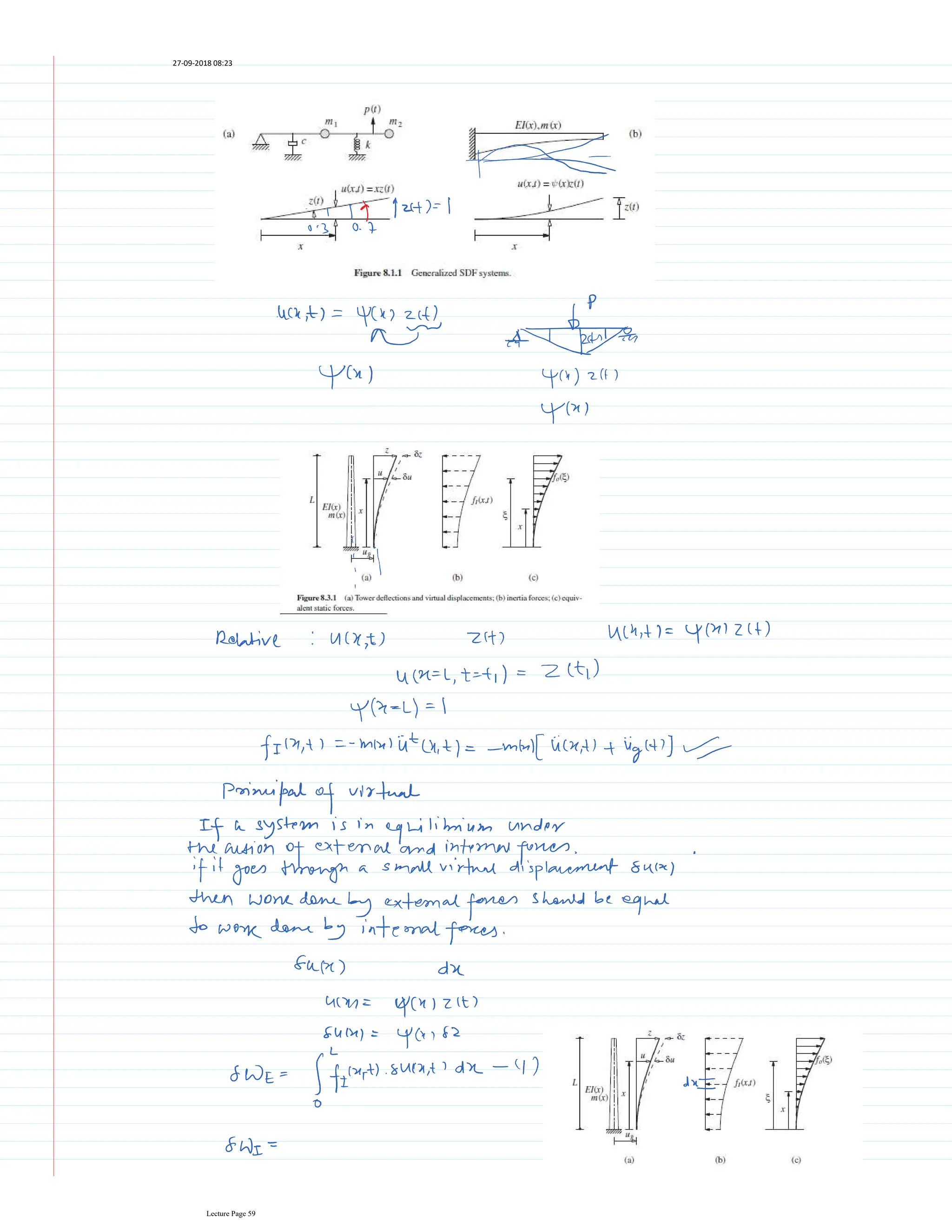
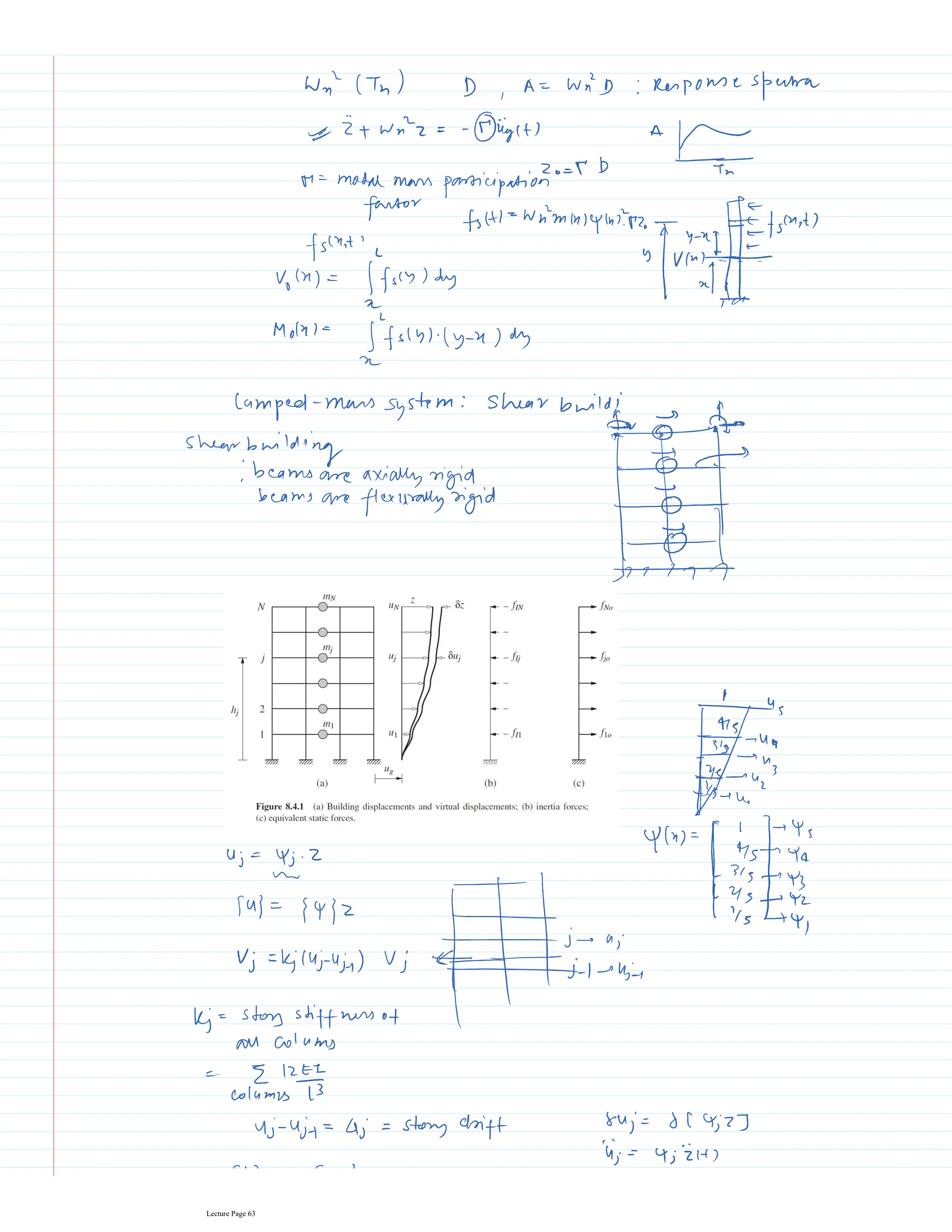
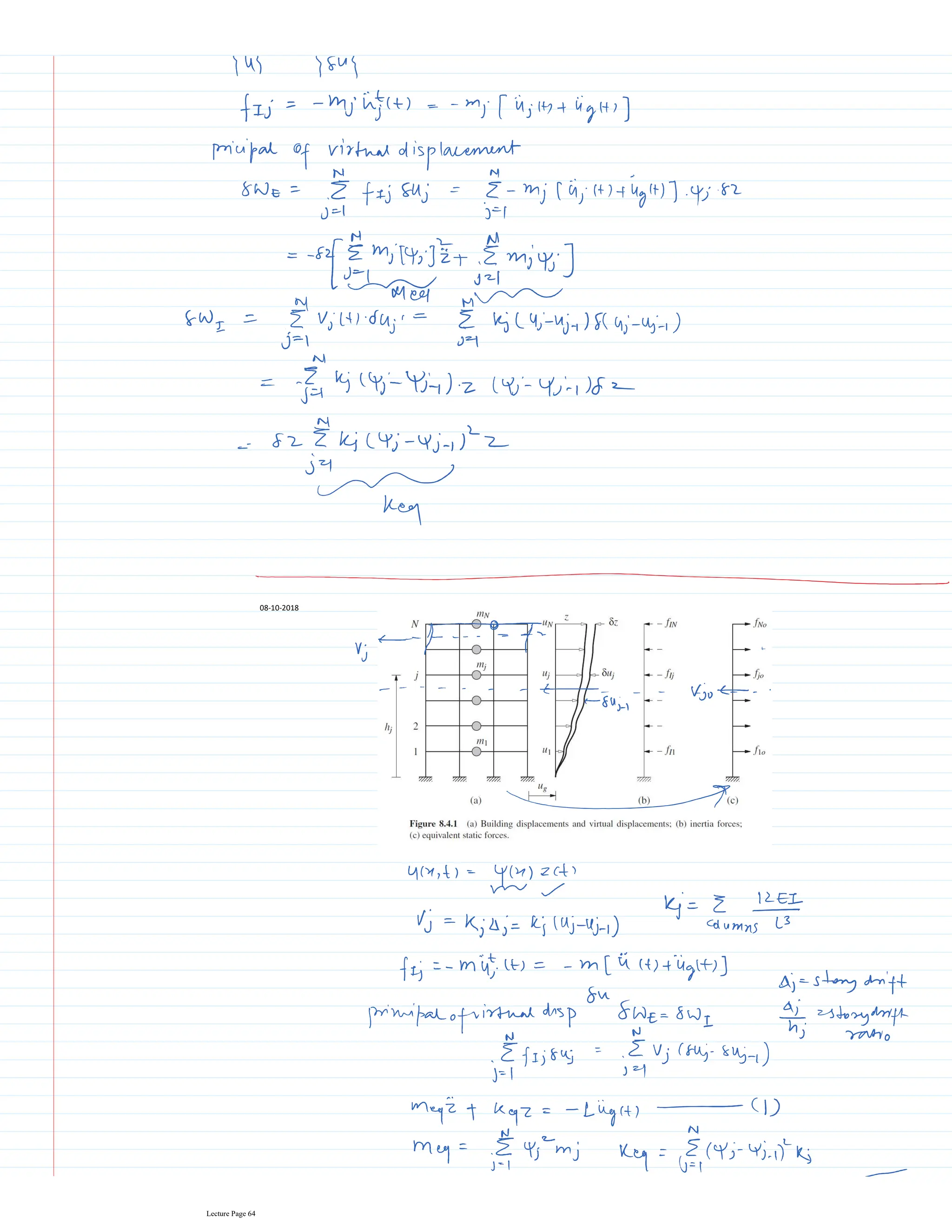
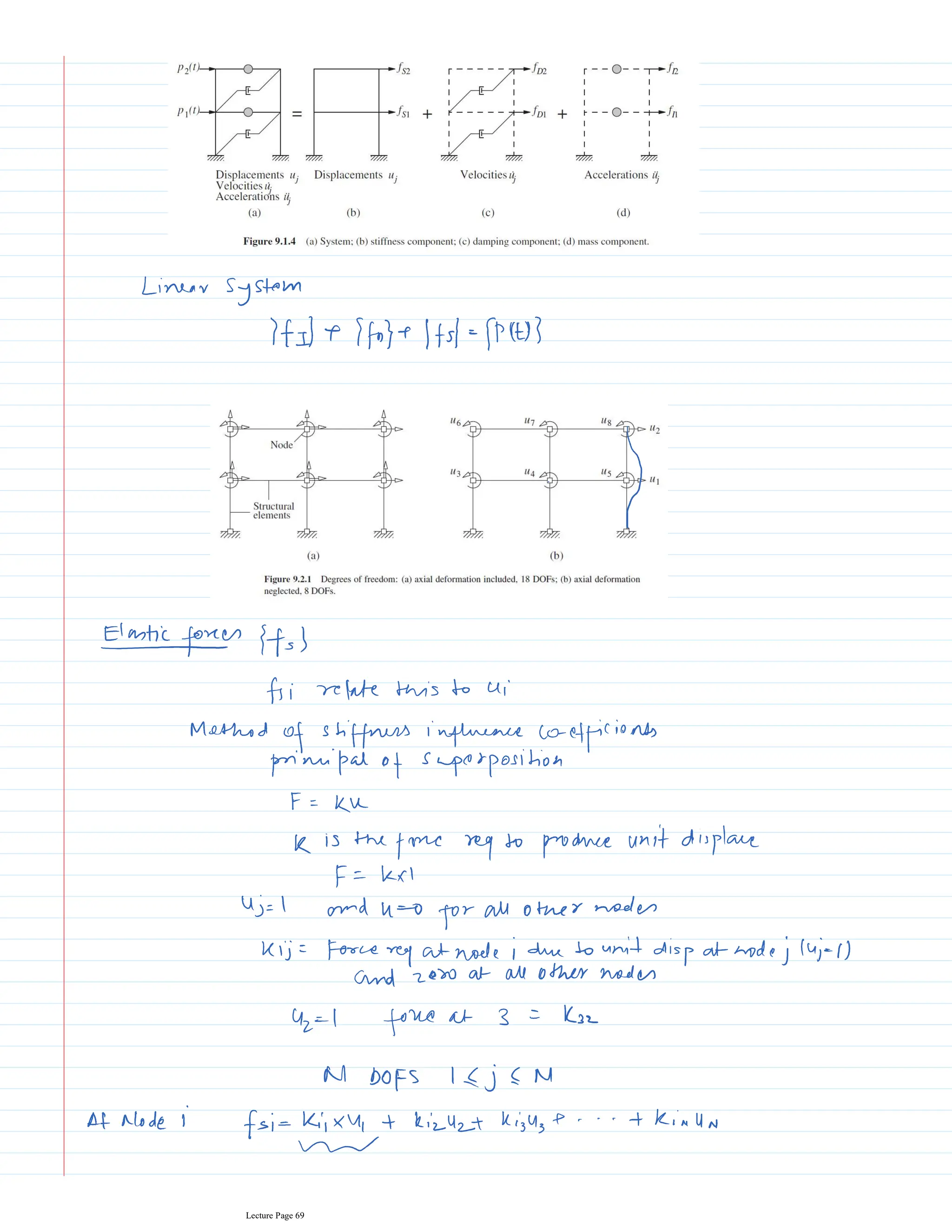
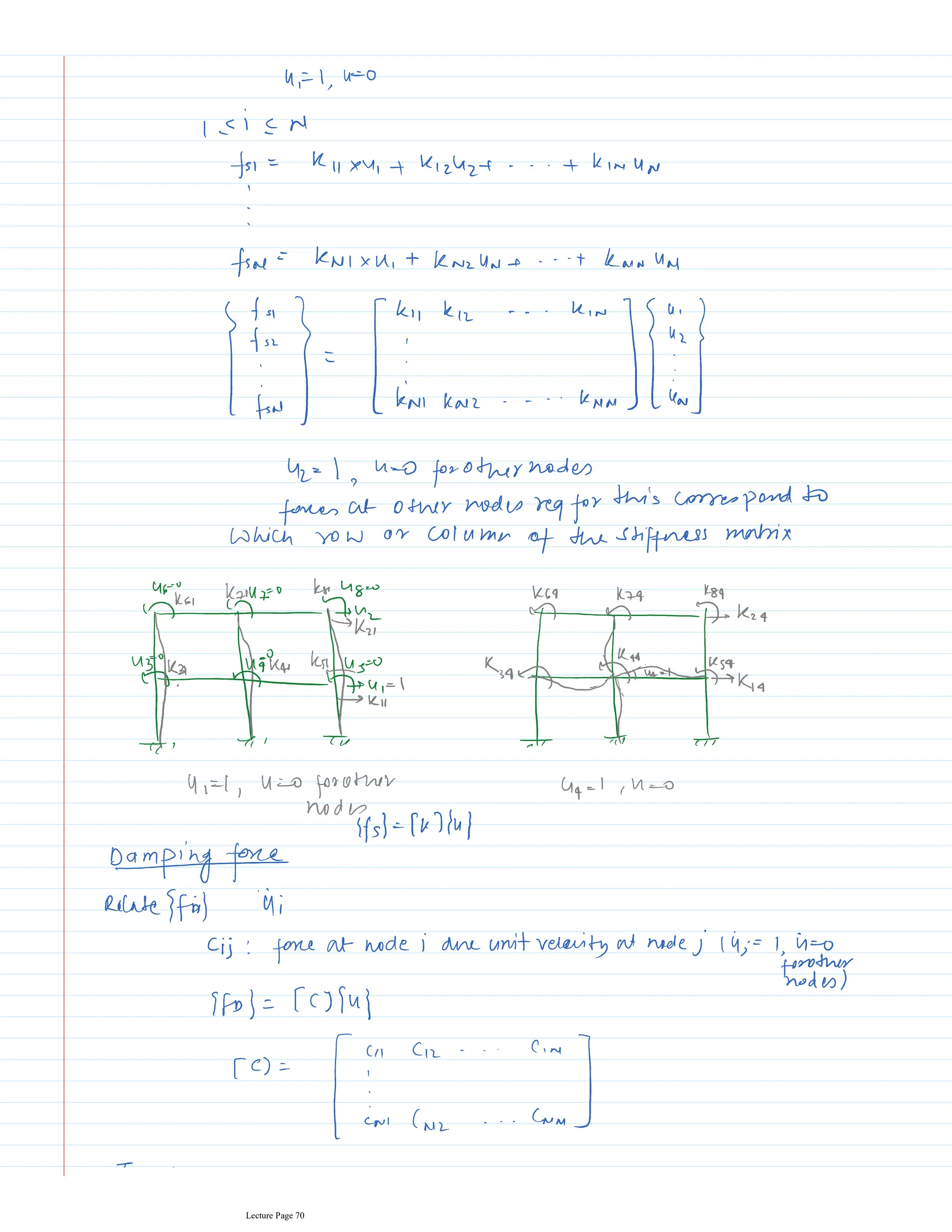
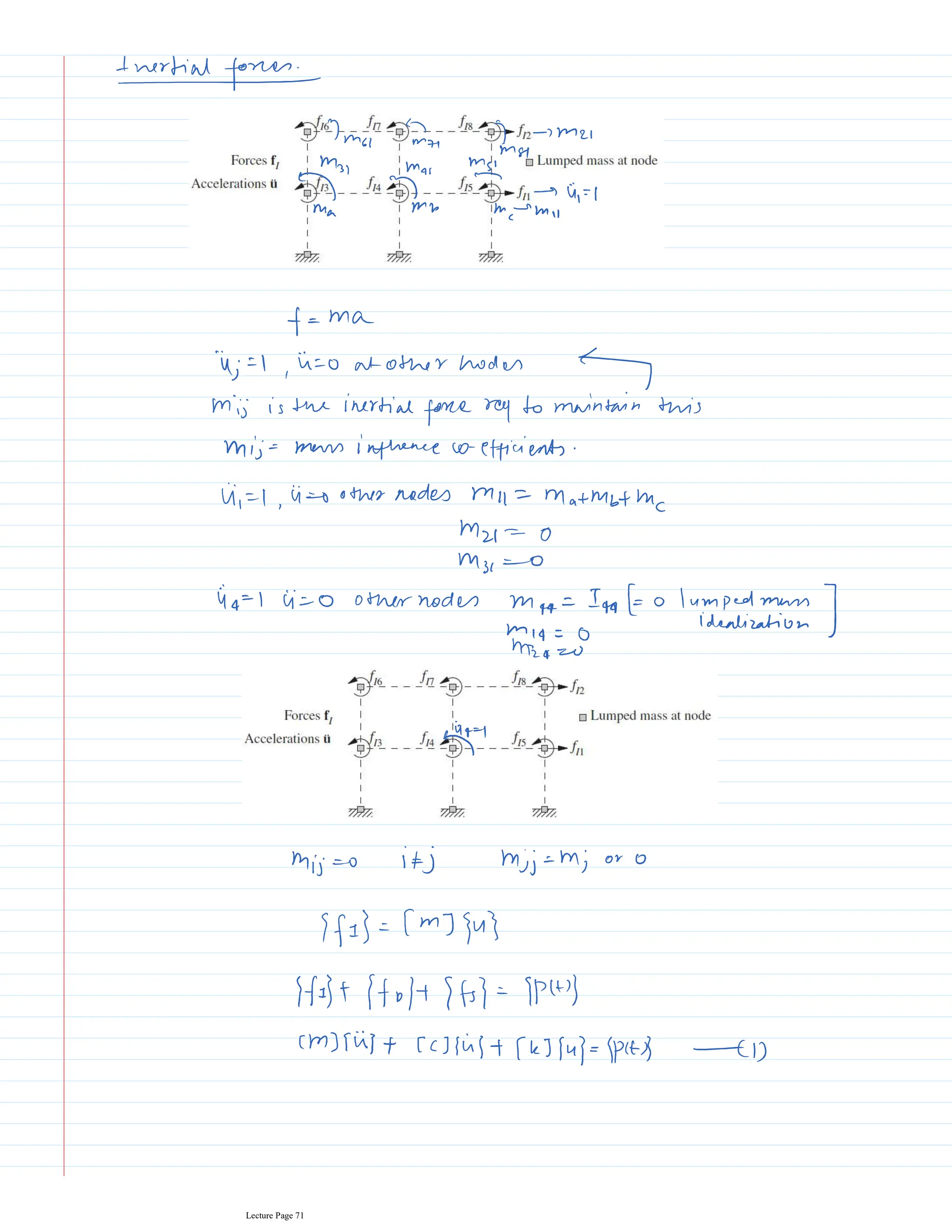
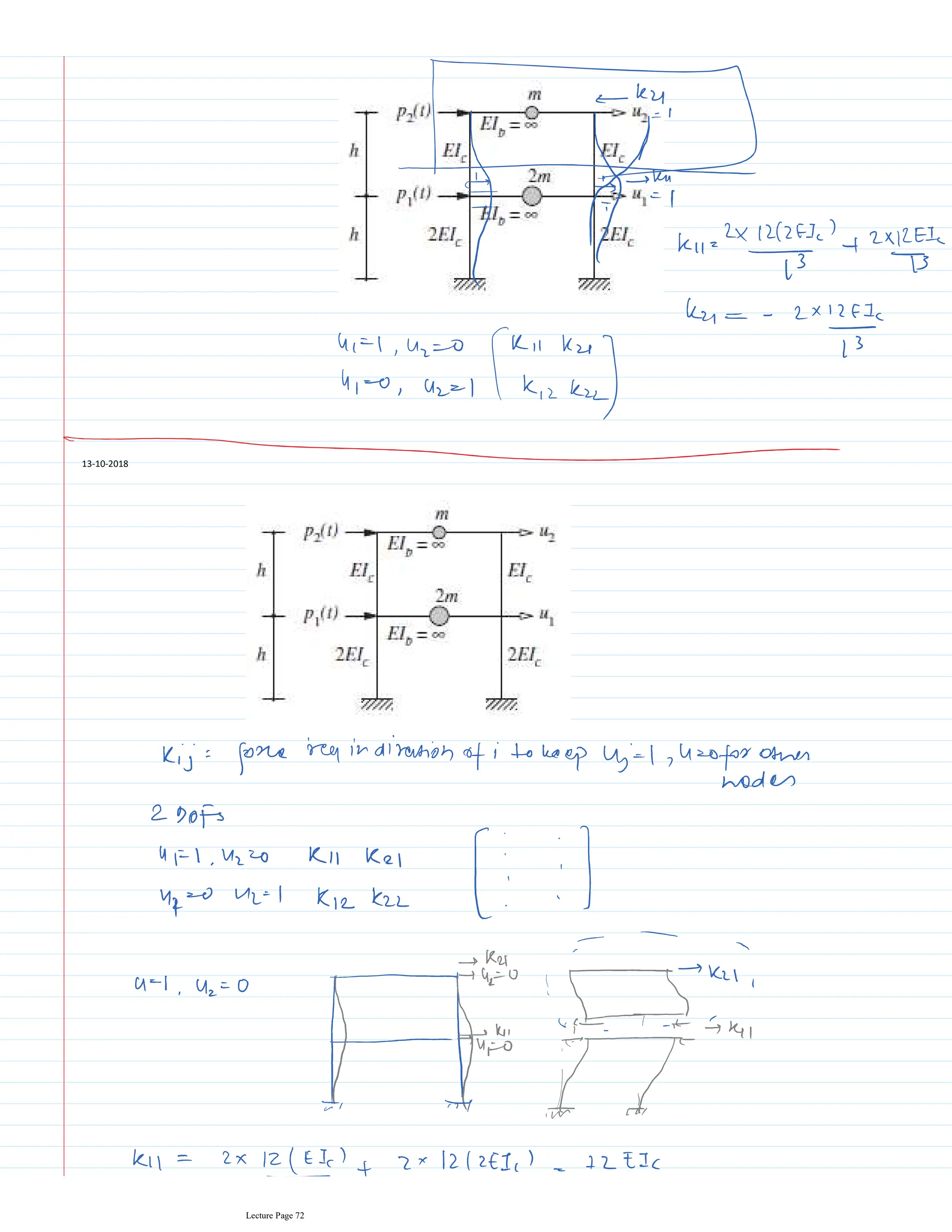
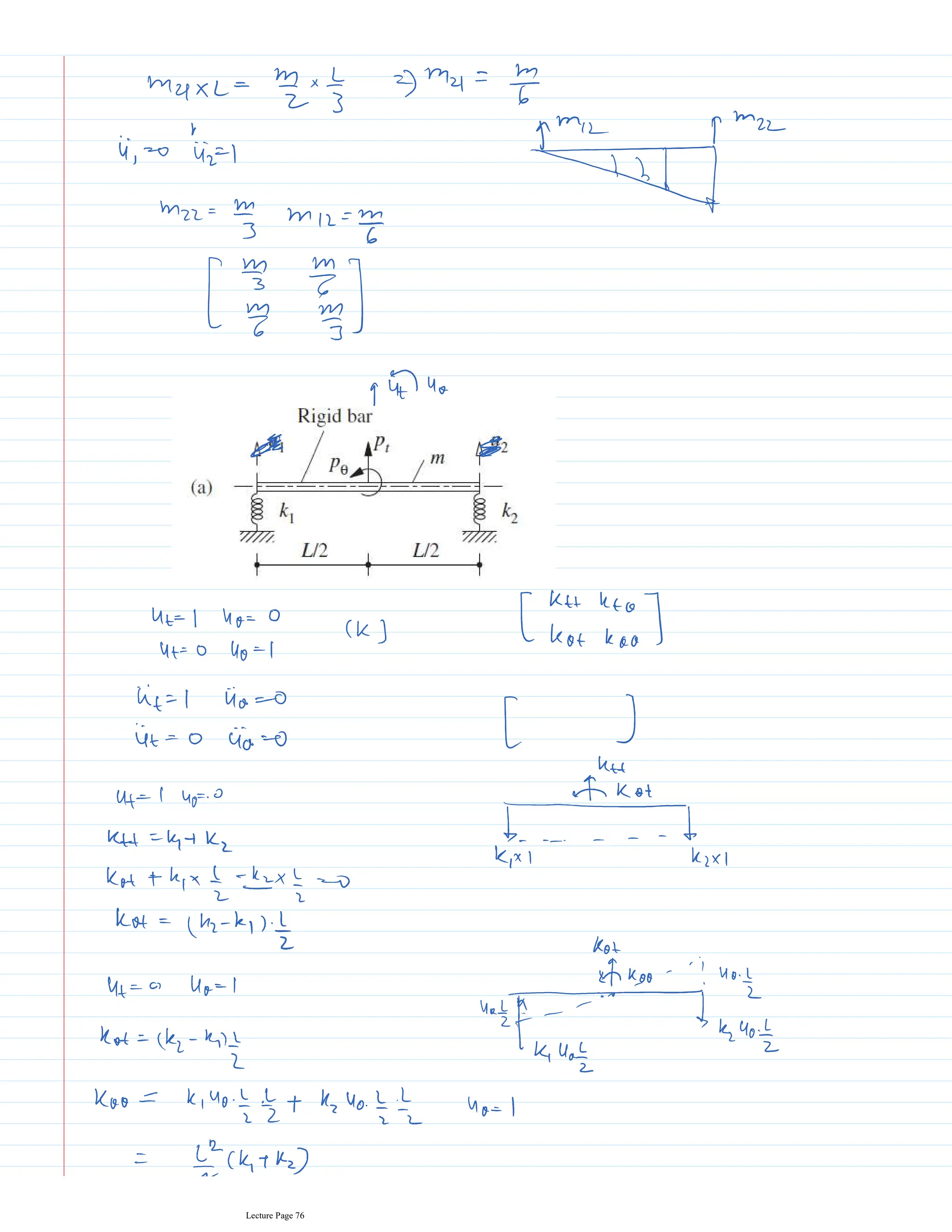
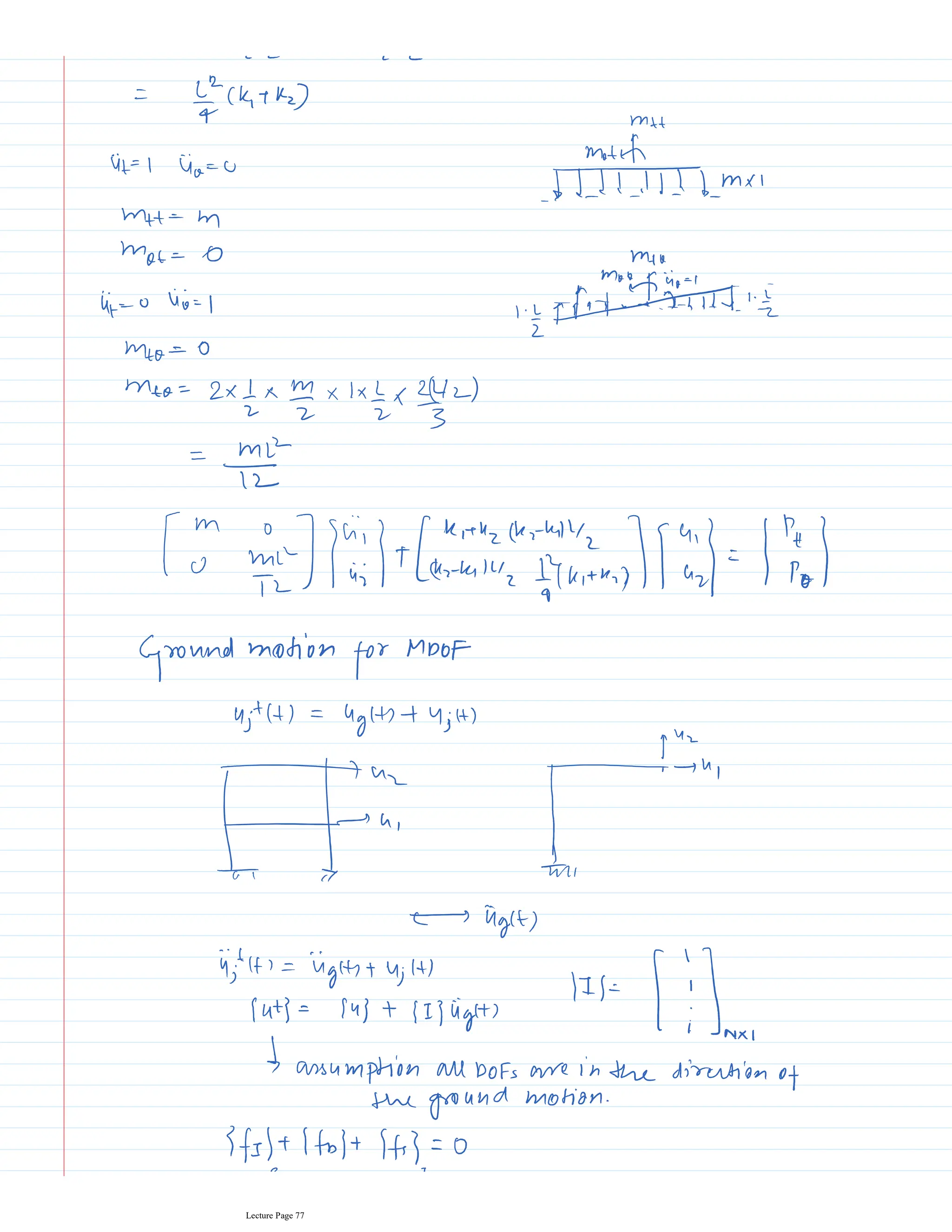
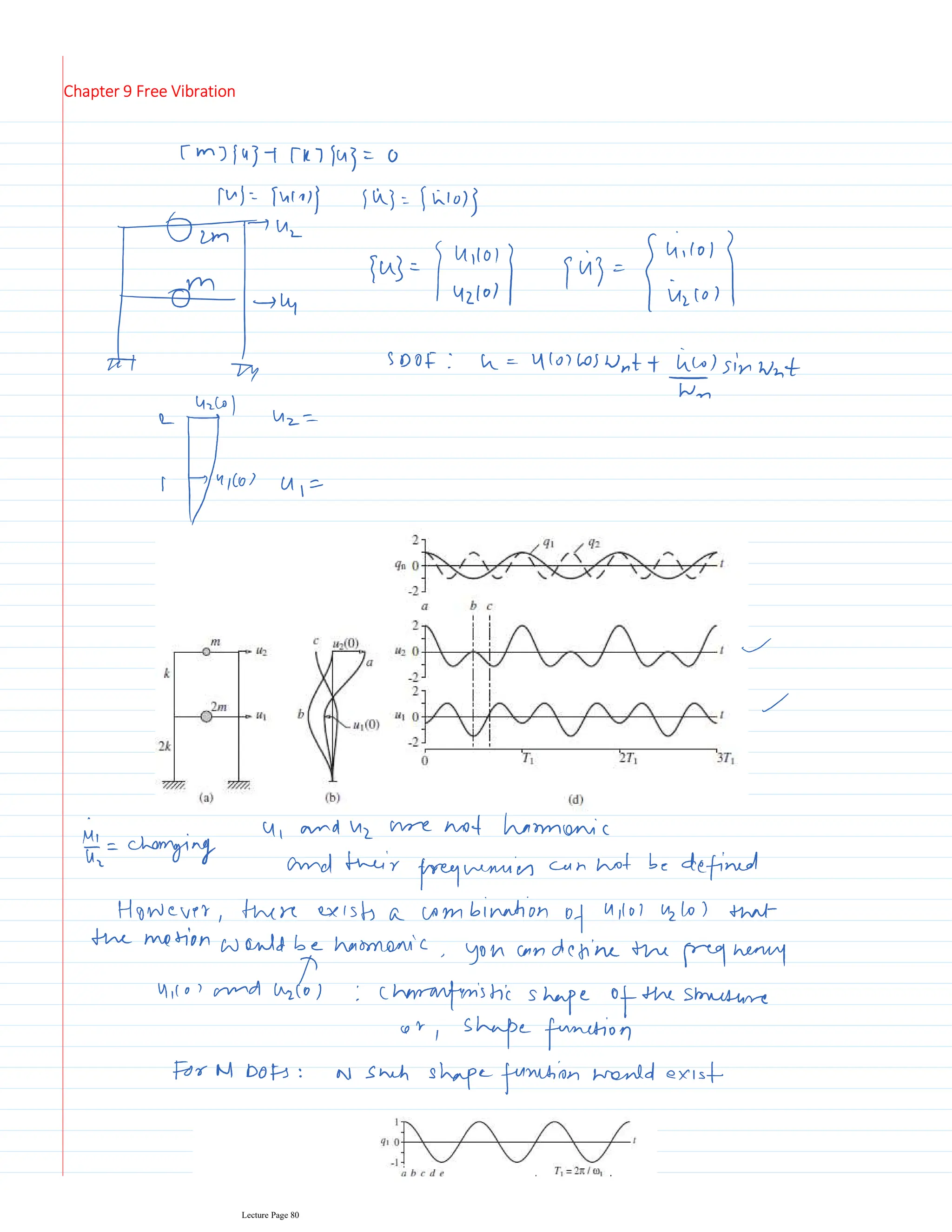
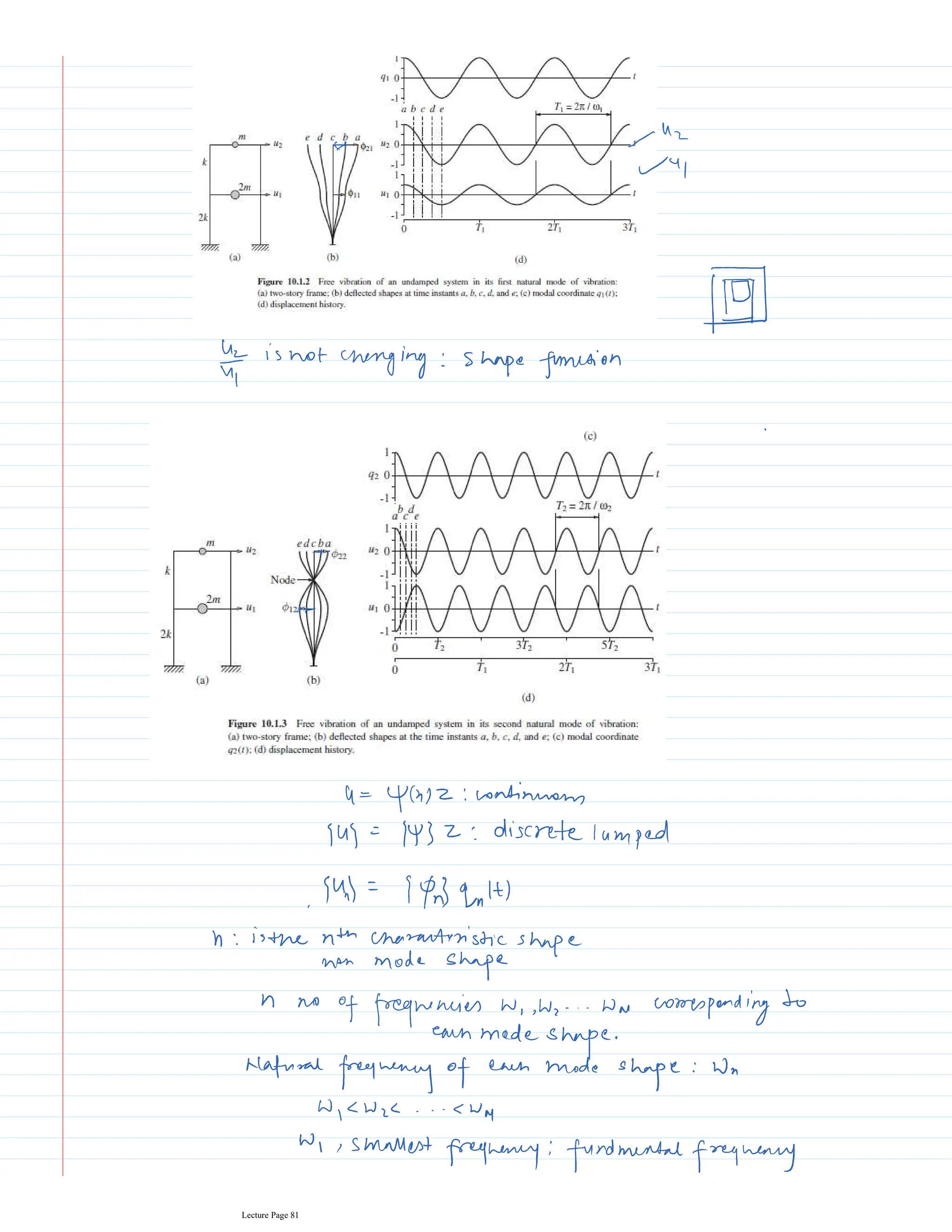
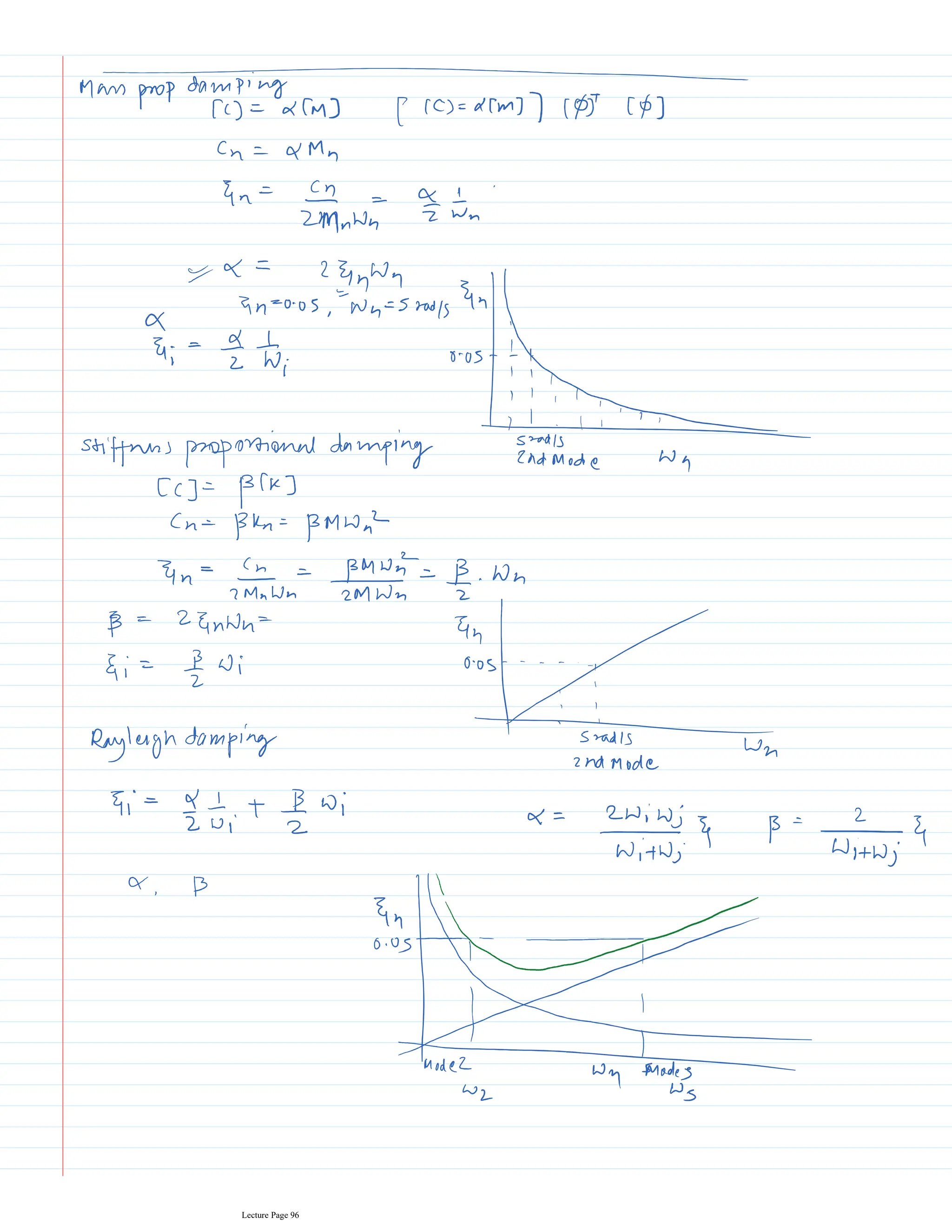
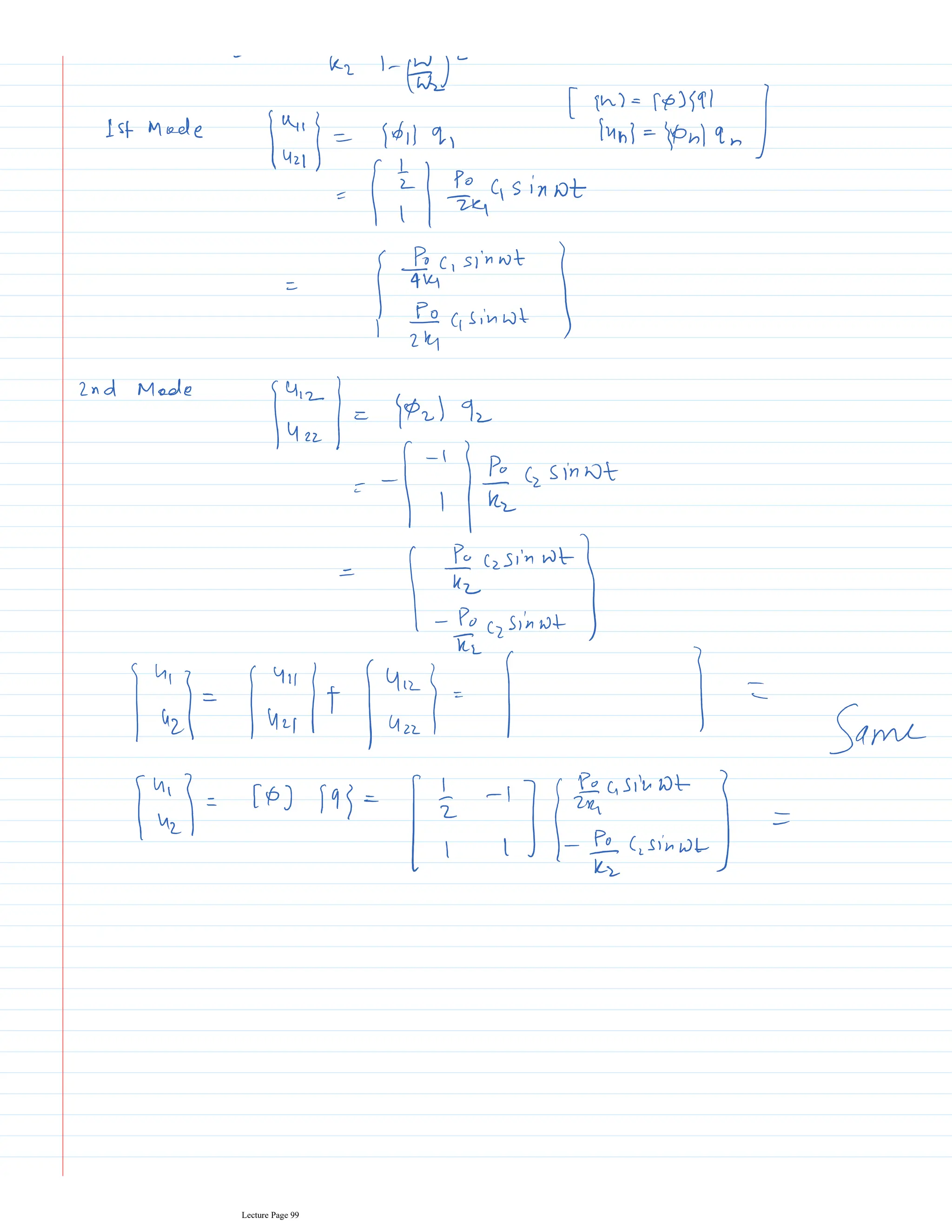
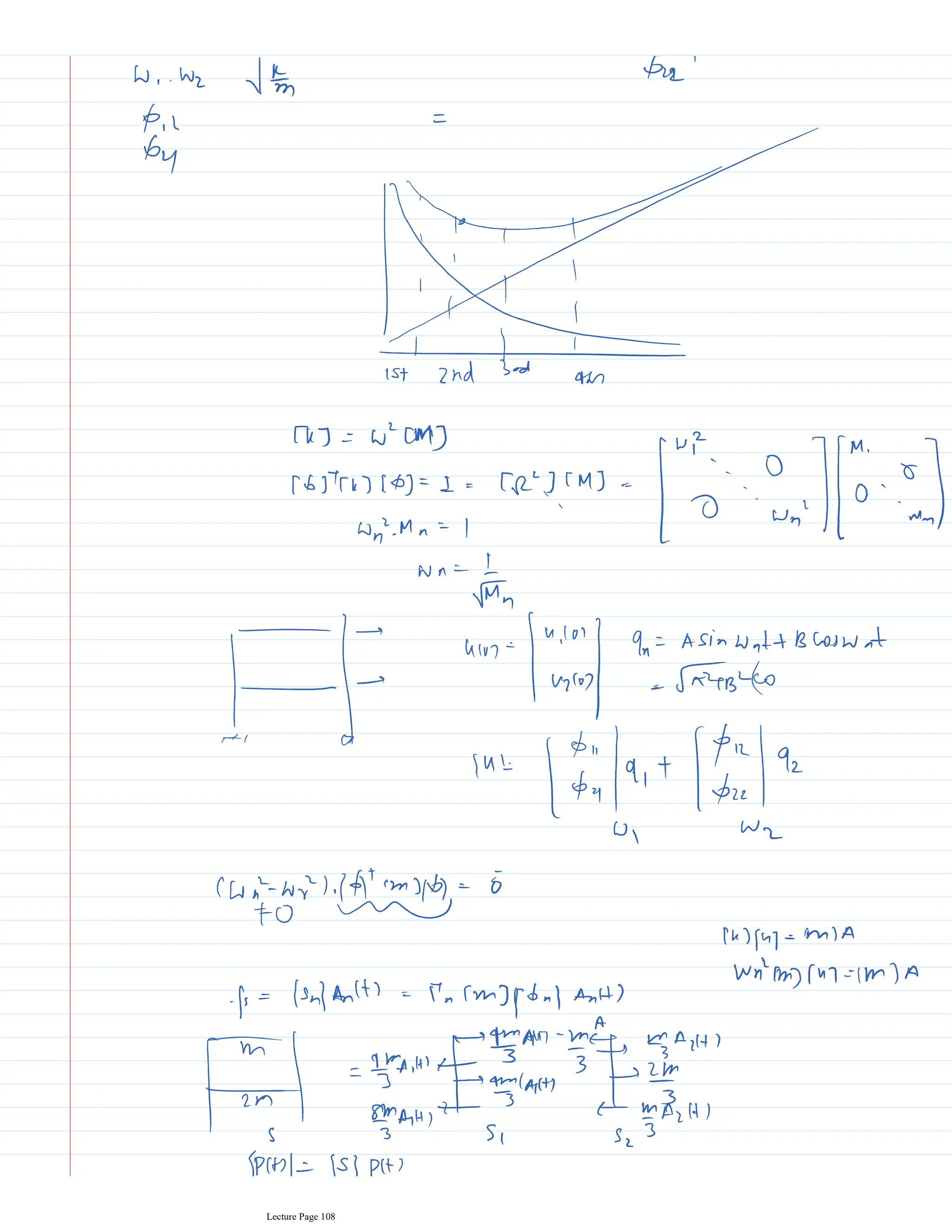
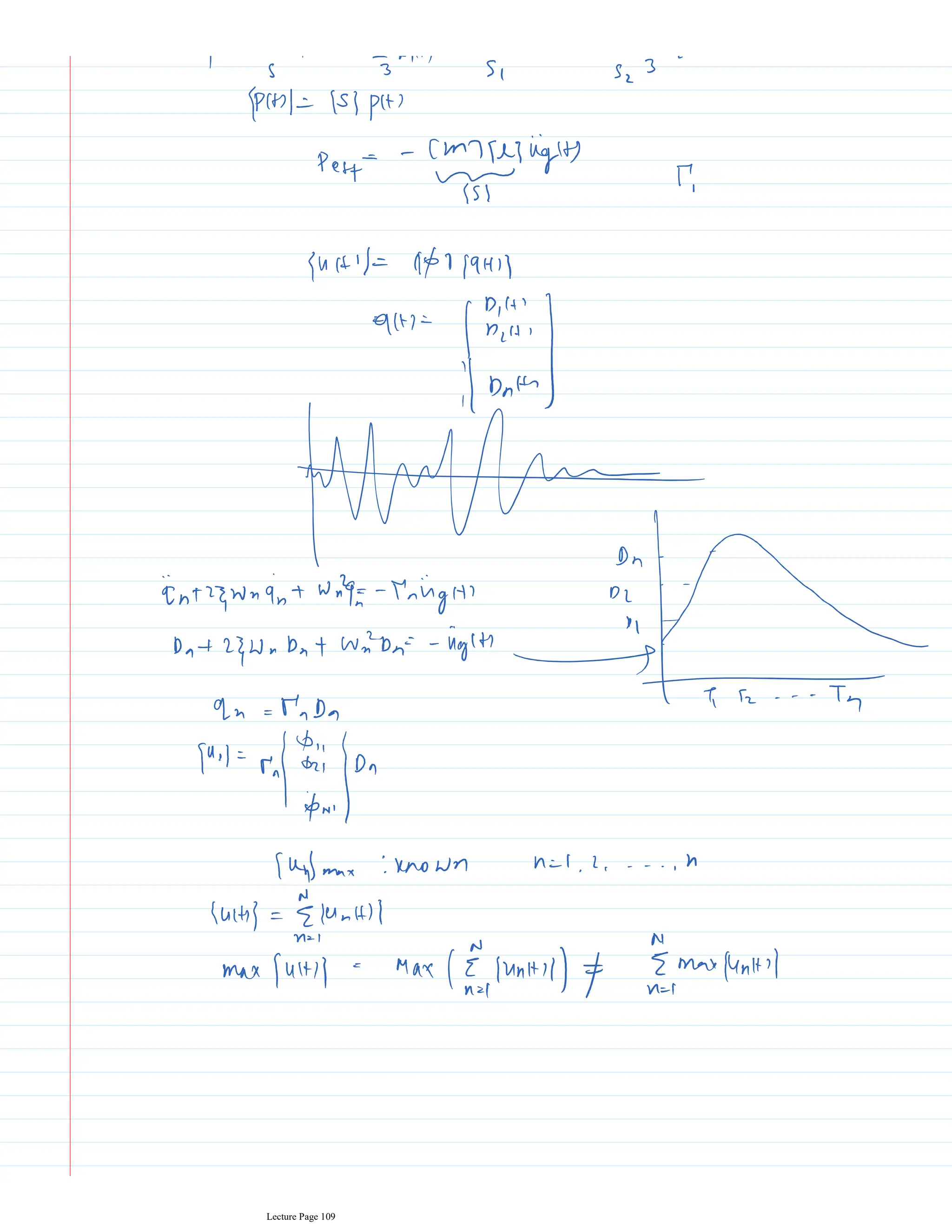
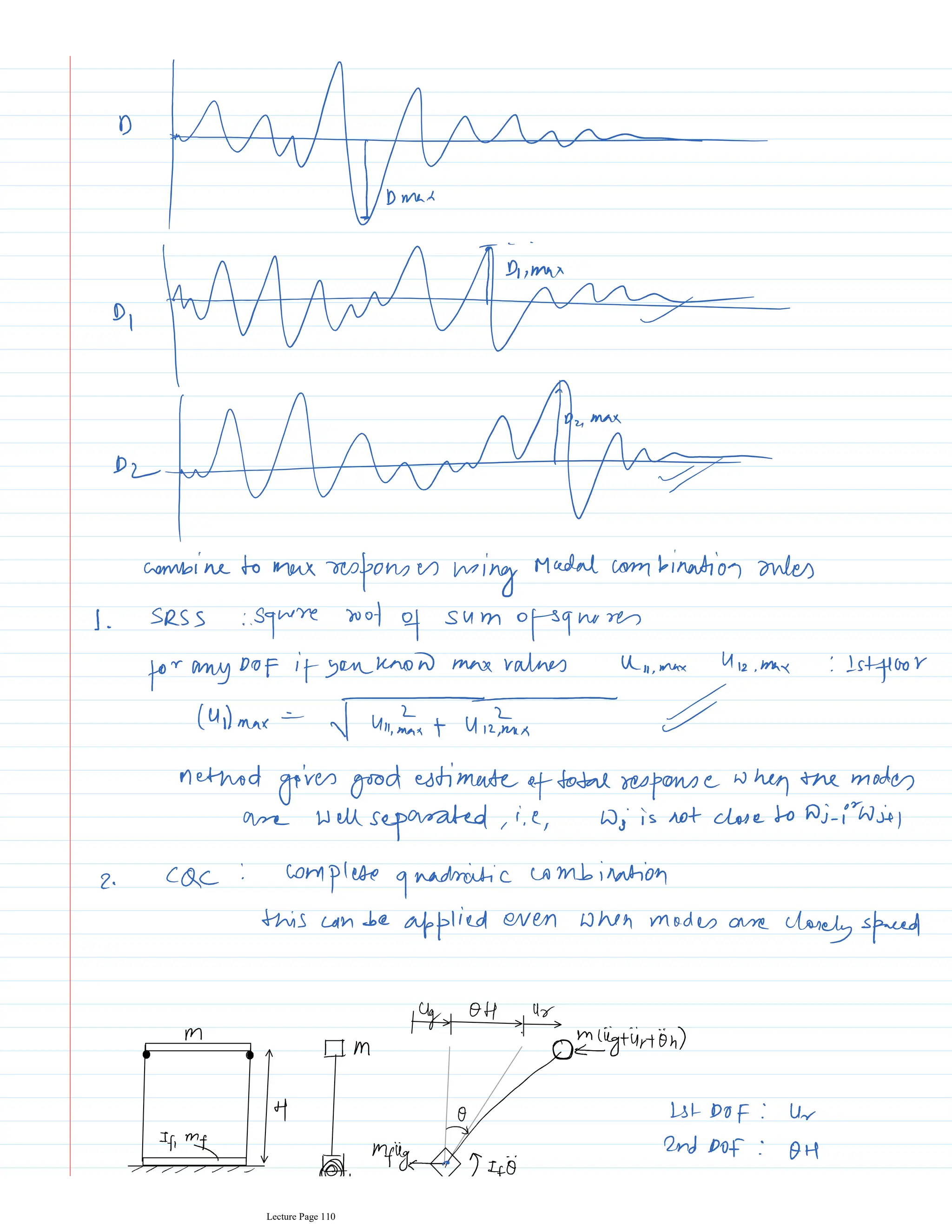
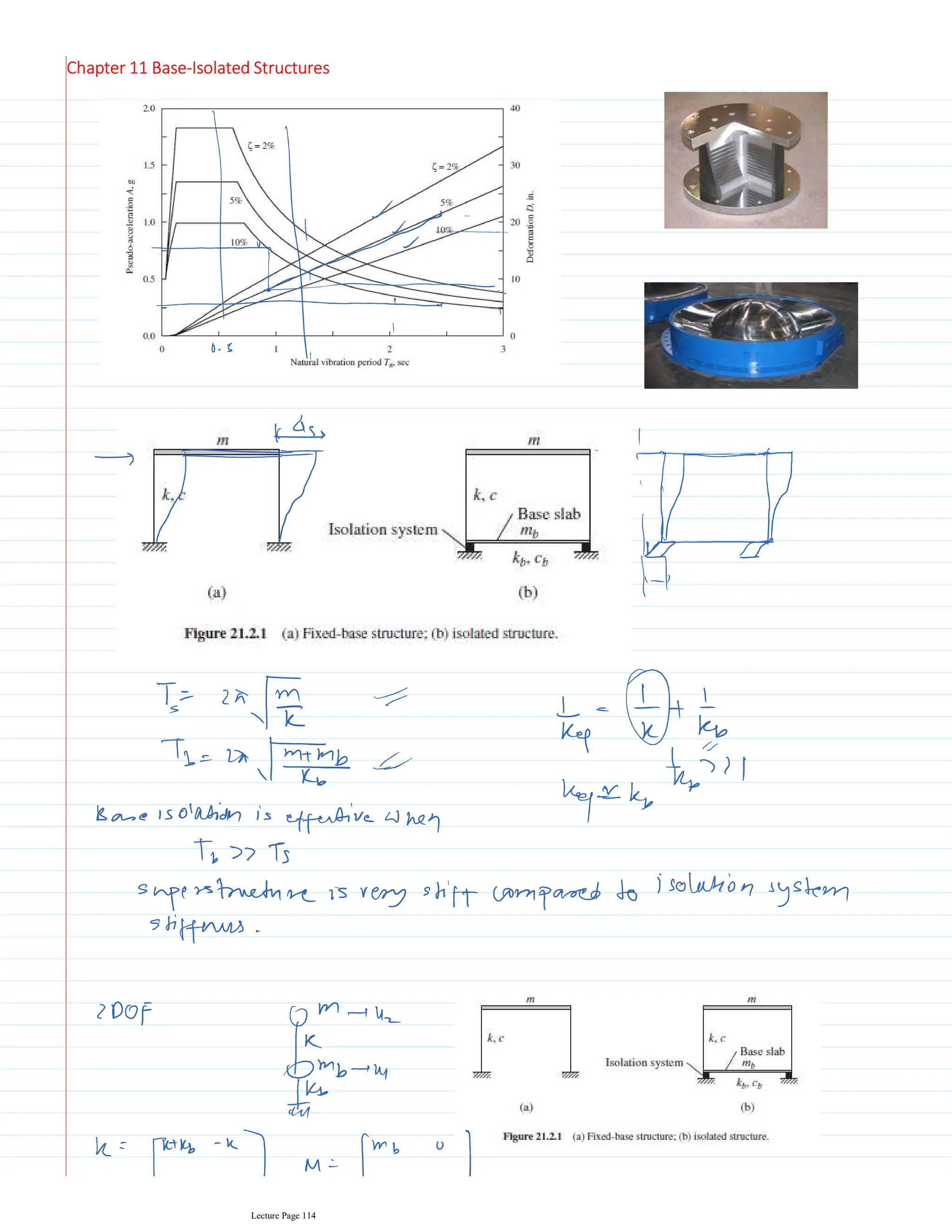
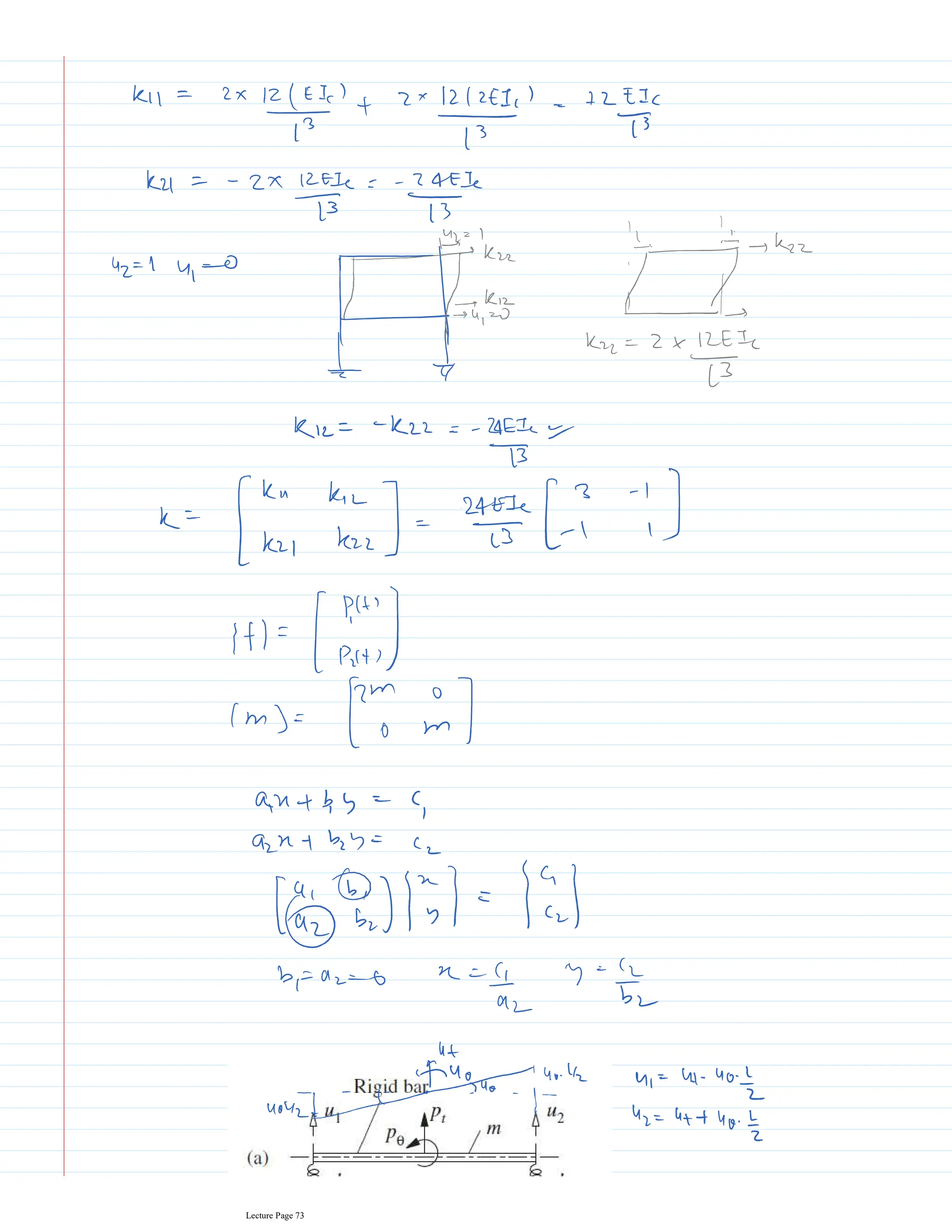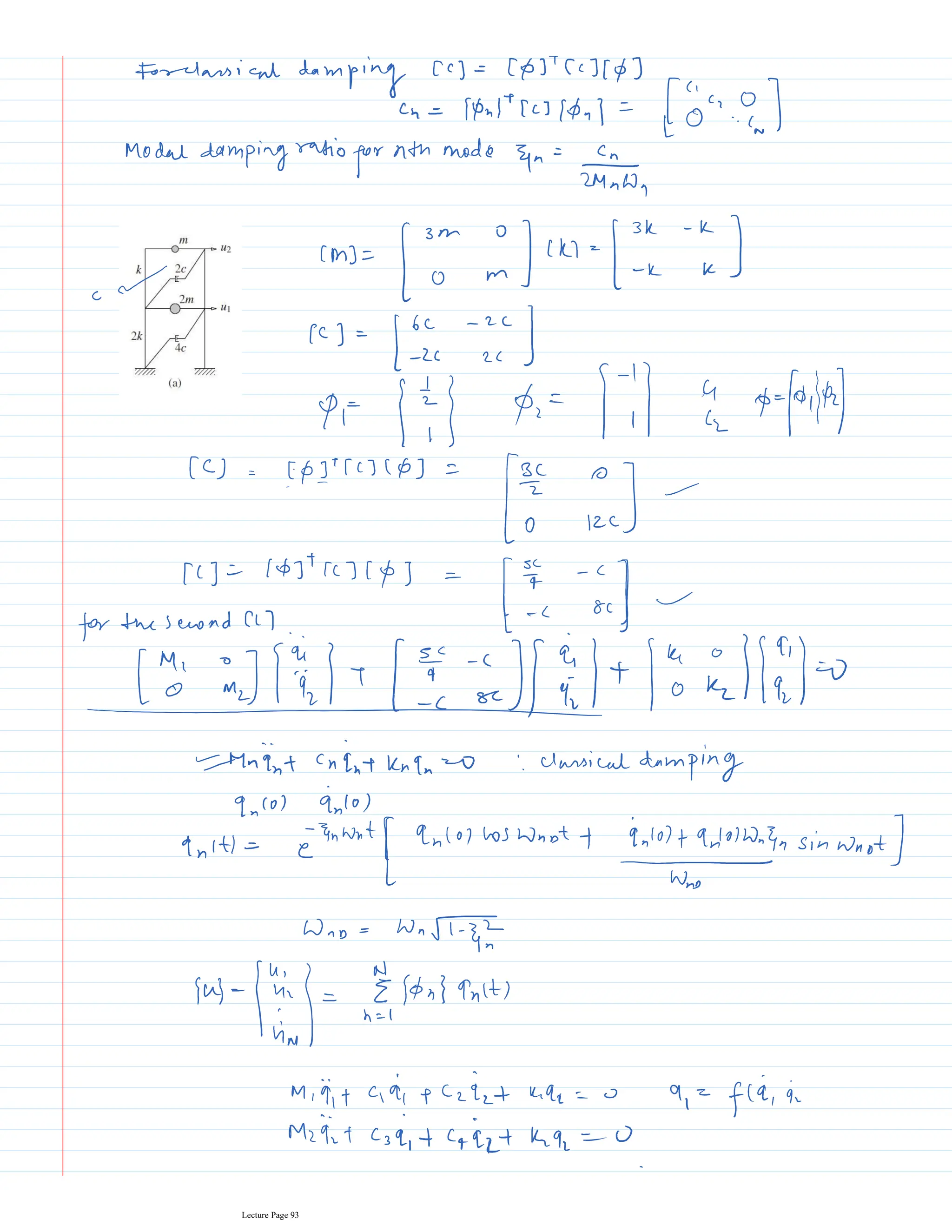This document appears to be lecture notes for a course on structural dynamics and earthquake engineering. It includes 13 chapters that cover topics such as single degree of freedom systems, free and forced vibration, multi-degree of freedom systems, numerical methods, base isolation, and earthquake response of structures. Each chapter contains multiple pages of lecture content, examples, and problems. The document provides an overview of the key concepts, methods, and analytical tools for analyzing the vibration and seismic behavior of structural systems.