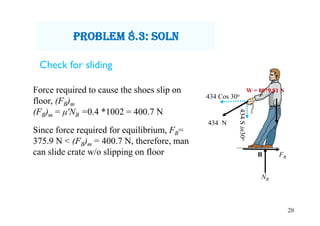
This document provides an overview of dry friction and Coulomb's theory of dry friction. It introduces key concepts such as static and kinetic friction, coefficients of friction, and limitations of Coulomb's model. Example problems are provided to demonstrate applications of dry friction analysis to determine equilibrium, potential for sliding or tipping, and minimum horizontal forces required to move objects. The document is from a engineering mechanics course focusing on rigid body analysis involving dry frictional forces.

1. University of Engineering and Technology
Peshawar, Pakistan
CE-117: Engineering Mechanics
MODULE 8:
Dry Friction
Prof. Dr. Mohammad Javed & Engr. Mudassir Iqbal
mjaved@uetpeshawar.edu.pk mudassiriqbal@uetpeshawar.edu.pk
1

2. Lecture Objectives
To introduce the concept of dry friction
and show how to analyse the equilibrium of
rigid bodies subjected to this force.

3. 3
 All real surfaces also provide a force component that is
tangent to the surface, called the friction force, that resists
sliding.
 Friction enables us:
 To walk without slipping,
 It holds nails and screws in place, and
 it allows us to transmit power by means of clutches and
belts.
 Friction can also be detrimental: It causes wear in machinery
and reduces efficiency in the transmission of power by
converting mechanical energy into heat.
frictiOn

4. 4
Dry friction (also known as Coulomb friction) refers to the
friction force that exists between two unlubricated solid
surfaces.
Fluid friction acts between moving surfaces that are
separated by a layer of fluid. The friction in a lubricated
journal bearing is classified as fluid friction, because the two
halves of the bearing are not in direct contact but are
separated by a thin layer of liquid lubricant.
frictiOn

5. 5
Dry friction is a complex phenomenon that is not yet
completely understood.
A detailed treatment of the nature of frictional forces
must also include the effects of temperature, density,
cleanliness, and atomic or molecular attraction between
the contacting surfaces.
This lecture introduces a highly simplified theory, known
as Coulomb’s theory of dry friction, that has been found
to give satisfactory results in many practical problems.
cOuLOmb’s theOry Of Dry frictiOn

6. 6
Body resting on rough
surface
F.B.D of body
Resultant of normal forces
and frictional resistance
cOuLOmb’s theOry Of Dry frictiOn

7. Coulomb proposed the following law: If there is no relative
motion between two surfaces that are in contact, the
normal force N and the friction force F satisfy the following
relationship.
7
Coulomb’s Theory
case 1: static cOnDitiOn
where Fmax (also abbreviated as
Fm) is the maximum static
friction force that can exist
between the contacting
surfaces and µs is known as the
coefficient of static friction. Static condition, Fs< Fm
Fm= μsN

8. 8
The coefficient friction is an experimental constant that depends
on the composition and roughness of the contacting surfaces.
typicaL vaLues Of cOefficient Of frictiOn

9. 9
Coulomb’s Theory
case 2: impenDing sLiDing
Motion Impending, Fs=Fm
Fm= μsN

10. 10
Coulomb’s Theory
case 3: Dynamic cOnDitiOn
Motion, Fk<Fm

11. 11
LimitatiOns Of cOuLOmb’s theOry

12. 12
LimitatiOns Of cOuLOmb’s theOry

13. 13
cOuLOmb’s theOry: summary
4 situations can occur when a rigid body is in contact with a horizontal surface:
1. No friction,(Px = 0)
,
(Px = Fm)
2. No motion
3. Motion Impending
4. Motion
Fm= μsN

14. 14
It is sometimes convenient to replace normal force N and friction
force F by their resultant R:
• No friction
• No motion • Motion• Motion impending
angLe Of frictiOn
when the block is on the verge of sliding,
the normal force N and frictional force Fm
combine to create a resultant Rs. The angle
ϕs that Rs makes with N is called the angle of
static friction.

15. 15
• Consider block of weight W resting on board with variable inclination
angle θ
• No friction • No motion • Motion
impending
• Motion
Angle of inclined surface at which the body is at the verge of sliding
in downward direction is known as Angle of Repose
angLe Of repOse

16. The uniform thin pole has a weight of 30 lb and a length of 26 ft.
If it is placed against the smooth wall and on the rough floor in
the position , will it remain in this position when it is released?
The coefficient of static friction is μs = 0.3
16
prObLem 8.1

17. 17
10ʹ
NB
30 lb
NA
FA
Bʹ
θ
prObLem 8.1: sOLutiOn
Assume Equilibrium

18. 18
10ʹ
NB
30 lb
NA
FA
Bʹ
θ
prObLem 8.1: sOLutiOn
5ʹ
Assume Equilibrium
30 *5 = 0

19. 19
prObLem 8.1: sOLutiOn
Check for siding

20. A horizontal force of P = 100 N is just sufficient to hold the
crate from sliding down the plane, and a horizontal force of
P = 350 N is required to just push the crate up the plane.
Determine the coefficient of static friction between the plane
and the crate, and find the mass of the crate.
20
prObLem 8.2

21. 21
100 Sin 30o
W
x’
y’
Case-I: When crate is at the verge
of sliding in downward direction
prObLem 8.2: sOLn

22. 22
350 Sin 30o
W
x’
y’
Case-II: When crate is at the verge
of sliding in upward direction
prObLem 8.2: sOLn
350Sin 30o

23. 23
By equating (II) and (IV)
By solving above eqn., we get m= 36.46 kg
Substituting value of m in (II) or (IV), we get μs = 0.256
prObLem 8.2: sOLn

24. The coefficient of static friction between the 150-kg crate
and the ground is μs = 0.3, while the coefficient of static
friction between the 80-kg man’s shoes and the ground is
μsʹ = 0.4. Determine if the man can move the crate.
24
prObLem 8.3

25. 25
T
NA
AFA
W
T Cos 30o
TSin30o
ΣFx = 0
T Cos 30o - FA = 0 -----------------(I)
In order to slide the crate, the magnitude of
T must be such that it produce FA= (FA)m
= μNA = 0.3NA
Substituting FA= 0.3NA in eqn. (I)
 T Cos 30o - 0.3NA = 0
 T = 0.346NA -------------(II)
prObLem 8.3: sOLn
Assume Equilibrium

26. 26
T
NA
AFA
W
T Cos 30o
TSin30o
ΣFy = 0
-W +NA+Tsin 30o= 0
-150*9.81 +NA+0.346NA Sin 30o= 0
NA = 1254.5 N
=> T = 0.346NA = 0.346*1254.5= 434 N
prObLem 8.3: sOLn
Assume Equilibrium

27. 27
ΣFy = 0
NB -80*9.81 -434 Sin 30o= 0
NB= 1002 N
434 Cos 30o
434Sin30o
434 N
B
NB
FB
W = 80*9.81 N
ΣFx = 0
-434 Cos 30o + FB = 0
FB = 375.9 N
prObLem 8.3: sOLn
Assume Equilibrium

28. 28
434 Cos 30o
434Sin30o
434 N
B
NB
FB
W = 80*9.81 NForce required to cause the shoes slip on
floor, (FB)m
(FB)m = μʹNB =0.4 *1002 = 400.7 N
Since force required for equilibrium, FB=
375.9 N < (FB)m = 400.7 N, therefore, man
can slide crate w/o slipping on floor
prObLem 8.3: sOLn
Check for sliding

29. 29
ImpendIng TIppIng
Up till now, we restricted our attention to sliding; the possibility of
tipping was neglected. We now discuss problems that include both
sliding and tipping as possible motions.
We wish to determine the magnitude of P that will cause impending
motion of the block, either impending sliding or impending tipping.

30. 30
ImpendIng TIppIng

31. The man in Figure is trying to
move a packing crate across the
floor by applying a horizontal force
P. The center of gravity of the 250-
N crate is located at its geometric
center. Does the crate move if P =
60 N? The coefficient of static
friction between the crate and the
floor is 0.3.
31
prObLem 8.4

32. If the block is assumed to remain in
equilibrium, the three equilibrium
equations can be used to calculate
the three unknowns:
1. the normal force N1,
2. the friction force F1,
3. and the distance x locating the line of
action of N1.
32
prObLem 8.4: sOLn

33. Assume Equilibrium
33
prObLem 8.4: sOLn

34. Check for overturning
The largest possible value for x is 0.3 m (half the width of
the crate). Because x = 0.216 m, as obtained from
equilibrium analysis, is smaller than that, we conclude that
the block will not tip.
Check for sliding
The limiting static friction force is (F1)max = µs N1 =
0.3(250) = 75.0 N, which is larger than the force F1 = 60 N
that is required for equilibrium. We therefore conclude
that the crate will not slide. 34
prObLem 8.4: sOLn

35. 35
Two concrete blocks weighing
320 lb each form part of the
retaining wall of a swimming
pool. Will the blocks be in
equilibrium when the pool is
filled and the water exerts the
line loading shown?
prObLem 8.5

36. Assume upper block in equilibrium
36
ΣFx= 0
F1-R1= 0 ---------(I)
R1 = ½*P1*8
prObLem 8.5: sOLn
N1
5 ̋
C
x1
F1
320 lb
P1
R1
h1 = 8/3̋
P1
Where P1/18= 32/36 or P1 = 16 lb/ft
R1 = ½*16*18 = 144 lb
 Eqn I: F1-144= 0
 F1=144 lb

37. Assume upper block in Equilibrium
37
ΣFy= 0
N1-320= 0 ---------(II)
N1 = 320 lb
ΣMC= 0
N1* x1 - R1*18/3= 0
320* x1-144*18/3= 0
x1 = 2.7 in
prObLem 8.5: sOLn
N1
5 ̋
C
x1
F1
320 lb
P1
R1
h1 = 18/3̋

38. 38
prObLem 8.5: sOLn
Check for sliding of upper block
Force required for sliding, (F1)max= μs1*N1 = 0.5*320 =160 lb <
Force required for equilibrium , F1= 144 lb so the upper block will
not slide
Check for Overturning of upper block
x1 for equilibrium = 1.2 in < half the length of block = 5 in
So the upper block will not over turn

39. 39
prObLem 8.5: sOLn
N1
5 ̋
C
x2
F2
640 lb
R2
h2 = 36/3̋
N2
Assume lower block in equilibrium
ΣFx= 0
F2-R2= 0 ---------(III)
R2 = ½*32*16 = 576 lb
 Eqn III: F2-576= 0
 F2=576 lb

40. 40
Assume lower block in equilibrium
N1
5 ̋
Cʹ
x2
F2
640 lb
R2
h2 = 36/3̋
N2
prObLem 8.5: sOLn
ΣFy= 0
N2-640= 0 ---------(IV)
N1 = 640 lb
ΣMCʹ= 0
N2* x2 – R2*36/3= 0
640* x2-576*36/3= 0
x2 = 10.8 in

41. 41
Check for sliding of lower block
Force required for sliding, (F2)max= μs2*N2 = 1.0*640 =640 lb <
Force required for equilibrium , F2= 576 lb so the lower block will
not slide
Check for Overturning of lower block
x2 for equilibrium = 10.8 in > half the length of block = 5 in
So the lower block will over turn
prObLem 8.5: sOLn

42. 42
exercise 8
Ans: μs =0.231
Ans: P= 0.127 lb
8.1
8.2

43. 43
Ans: θ =16.3o
exercise 8
8.3

44. 44
Ans: FD= 36.9 lb, Ay= 468 lb,
Bx= 34.6 lb, By= 228 lb
exercise 8
8.4

45. 45
Ans: x= 4.34 ft
exercise 8
8.5

46. 46
Ans: P= 153.2 N
exercise 8
8.6

47. 47
Ans: P= 115.3 N
exercise 8
8.7

48. 48
Ans: P =60 lb
exercise 8
8.8

49. 49
exercise 8
8.9
Ans: P =29.5 N

50. hOme assignment 8
 Section B: 1,5 and 7
 Section D: 2,6 and 8
50