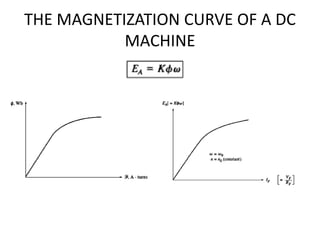
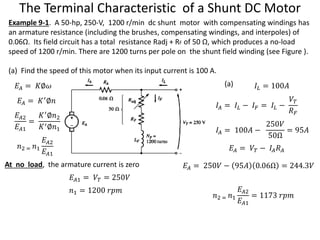
This document discusses direct current (DC) electrical machines. It covers the equivalent circuit of a DC motor, the magnetization curve of a DC machine, and different types of DC motors including separately excited, shunt, permanent magnet, series, and compounded DC motors. The key characteristics and behaviors of shunt DC motors are analyzed through examples, including the effect of armature reaction and derivation of the torque-speed curve. Nonlinear analysis is also demonstrated for a shunt motor without compensating windings.

1. IE243 ELECTRICAL MACHINES–I
[Cr. Hrs = 2+1] [Marks: 100+50]
By
Asif Ahmed Memon

2. Introduction to DC motors

3. Speed Regulation

4. • THE EQUIVALENT CIRCUIT OFADC MOTOR
• THE MAGNETIZATION CURVE OF A DC
MACHINE
• Type of dc motors
– SEPARATELY EXCITED AND SHUNT DC MOTORS
– THE PERMANENT-MAGNET DC MOTOR
– THE SERIES DC MOTOR
– THE COMPOUNDED DC MOTOR

5. THE EQUIVALENT CIRCUIT OF A DC
MOTOR

6. • THE EQUIVALENT CIRCUIT OFADC MOTOR
• THE MAGNETIZATION CURVE OF A DC
MACHINE
• Type of dc motors
– SEPARATELY EXCITED AND SHUNT DC MOTORS
– THE PERMANENT-MAGNET DC MOTOR
– THE SERIES DC MOTOR
– THE COMPOUNDED DC MOTOR

7. THE MAGNETIZATION CURVE OF A DC
MACHINE

8. • THE EQUIVALENT CIRCUIT OFADC MOTOR
• THE MAGNETIZATION CURVE OF A DC
MACHINE
• Type of dc motors
– SEPARATELY EXCITED AND SHUNT DC MOTORS
– THE PERMANENT-MAGNET DC MOTOR
– THE SERIES DC MOTOR
– THE COMPOUNDED DC MOTOR

9. SEPARATELY EXCITED AND SHUNT DC MOTORS

10. The Terminal Characteristic of a Shunt DC Motor
• A terminal characteristic of a machine is a plot
of the machine's output quantities versus
each other.
• For a motor, the output quantities are shaft
torque and speed,
• so the terminal characteristic of a motor is a
plot of its output torque versus speed.

11. The Terminal Characteristic of a Shunt DC Motor
• How does a shunt dc motor respond to a load?
the load on the shaft of a
shunt motor is increased
At steady state 𝜏𝑙𝑜𝑎𝑑 = 𝜏𝑖𝑛𝑑
𝜏𝑙𝑜𝑎𝑑 > 𝜏𝑖𝑛𝑑
the motor will start
to slow down
When the motor slows
down, its internal
generated voltage drops
𝐸𝐴 = 𝐾∅𝜔 ↓
so the armature current
in the motor increases 𝐼𝐴 = (𝑉𝑇 − 𝐸𝐴 ↓ ) 𝑅 𝐴
As the armature current
rises, the induced torque
in the motor increases
𝜏𝑖𝑛𝑑 = 𝐾∅𝐼𝐴 ↑
and finally the induced torque will equal the load torque at a lower mechanical
speed of rotation ω

12. The Terminal Characteristic of a Shunt DC Motor
The output characteristic of a shunt dc motor can be derived from the induced voltage
and torque equations of the motor plus Kirchhoff's voltage law. (KVL)
The KVL equation
for a shunt motor is
𝑉𝑇 = 𝐸𝐴 + 𝐼𝐴 𝑅 𝐴
The induced voltage 𝐸𝐴 = 𝐾∅𝜔
𝑉𝑇 = 𝐾∅𝜔 + 𝐼𝐴 𝑅 𝐴
Since 𝜏𝑖𝑛𝑑 = 𝐾∅𝐼𝐴
𝐼𝐴 =
𝜏𝑖𝑛𝑑
𝐾∅
Solve for IA
𝑉𝑇 = 𝐾∅𝜔 +
𝜏𝑖𝑛𝑑
𝐾∅
𝑅 𝐴
Therefore
Finally, solving for
the motor's speed
yields
𝜔 =
𝑉𝑇
𝐾∅
−
𝑅 𝐴
𝐾∅ 2
𝜏𝑖𝑛𝑑

13. The Terminal Characteristic of a Shunt DC Motor
𝜔 =
𝑉𝑇
𝐾∅
−
𝑅 𝐴
𝐾∅ 2
𝜏𝑖𝑛𝑑
• This equation is just a straight line with a negative
slope. The resulting torque- speed characteristic of
a shunt dc motor is shown in Figure
• If a motor has armature reaction, then as its load
increases, the flux-weakening effects reduce its
flux.
• As Equation shows, the effect of a reduction in flux
is to increase the motor's speed at any given load
over the speed it would run at without armature
reaction.
• The torque-speed characteristic of a shunt motor
with armature reaction is shown in Figure.
• If a motor has compensating windings, of course
there will be no flux-weakening problems in the
machine, and the flux in the machine will be
constant.

14. The Terminal Characteristic of a Shunt DC Motor
Example 9-1. A 50-hp, 250-V, 1200 r/min dc shunt motor with compensating windings has
an armature resistance (including the brushes, compensating windings, and interpoles) of
0.06Ω. Its field circuit has a total resistance Radj + RF of 50 Ω, which produces a no-load
speed of 1200 r/min. There are 1200 turns per pole on the shunt field winding (see Figure ).
(a) Find the speed of this motor when its input current is 100 A.
(b) Find the speed of this motor when its input current is 200 A.
(c) Find the speed of this motor when its input current is 300 A.
(d) Plot the torque-speed characteristic of this motor.
𝐸𝐴 = 𝐾∅𝜔
𝐸𝐴 = 𝐾′∅𝑛
𝐸𝐴2
𝐸𝐴1
=
𝐾′∅𝑛2
𝐾′∅𝑛1
𝑛2 = 𝑛1
𝐸𝐴2
𝐸𝐴1
At no load, the armature current is zero
𝐸𝐴1 = 𝑉𝑇 = 250𝑉
𝑛1 = 1200 𝑟𝑝𝑚

15. The Terminal Characteristic of a Shunt DC Motor
Example 9-1. A 50-hp, 250-V, 1200 r/min dc shunt motor with compensating windings has
an armature resistance (including the brushes, compensating windings, and interpoles) of
0.06Ω. Its field circuit has a total resistance Radj + RF of 50 Ω, which produces a no-load
speed of 1200 r/min. There are 1200 turns per pole on the shunt field winding (see Figure ).
(a) Find the speed of this motor when its input current is 100 A.
𝐸𝐴 = 𝐾∅𝜔
𝐸𝐴 = 𝐾′
∅𝑛
𝐸𝐴2
𝐸𝐴1
=
𝐾′
∅𝑛2
𝐾′∅𝑛1
𝑛2 = 𝑛1
𝐸𝐴2
𝐸𝐴1
At no load, the armature current is zero
𝐸𝐴1 = 𝑉𝑇 = 250𝑉
𝑛1 = 1200 𝑟𝑝𝑚
(a) 𝐼𝐿 = 100𝐴
𝐼𝐴 = 𝐼𝐿 − 𝐼 𝐹 = 𝐼𝐿 −
𝑉𝑇
𝑅 𝐹
𝐼𝐴 = 100𝐴 −
250𝑉
50Ω
= 95𝐴
𝐸𝐴 = 𝑉𝑇 − 𝐼𝐴 𝑅 𝐴
𝐸𝐴 = 250𝑉 − 95𝐴 0.06Ω = 244.3𝑉
𝑛2 = 𝑛1
𝐸𝐴2
𝐸𝐴1
= 1173 𝑟𝑝𝑚

16. The Terminal Characteristic of a Shunt DC Motor
Nonlinear Analysis of a Shunt DC Motor
Example 9-2. A 50-hp, 250-V, 1200 r/min dc shunt motor without compensating windings
has an armature resistance (including the brushes and interpoles) of 0.06 Ω. Its field circuit
has a total resistance RF + Radj of 50 Ω, which produces a no-load speed of 1200 r/min. There
are 1200 turns per pole on the shunt field winding, and the armature reaction produces a
demagnetizing magnetomotive force of 840 A • turns at a load current of 200 A. The
magnetization curve of this machine is shown in Figure .
(a) Find the speed of this motor when its input
current is 200 A.
(b) This motor is essentially identical to the
one in Example 9- 1 except for the absence of
compensating windings. How does its speed
compare to that of the previous motor at a
load current of 200 A?
(c) Calculate and plot the torque-speed
characteristic for this motor.

17. The Terminal Characteristic of a Shunt DC Motor
Nonlinear Analysis of a Shunt DC Motor
(a) Find the speed of this motor when its input
current is 200 A.
If IL = 200 A, then the armature current of the
motor is
𝐼𝐴 = 𝐼𝐿 − 𝐼 𝐹 = 𝐼𝐿 −
𝑉𝑇
𝑅 𝐹
= 195𝐴
𝐸𝐴 = 𝑉𝑇 − 𝐼𝐴 𝑅 𝐴 = 238.3 V
At IL = 200 A, the demagnetizing magneto
motive force due to armature reaction is 840 A
· turns, so the effective shunt field current of
the motor is

18. The Terminal Characteristic of a Shunt DC Motor
Nonlinear Analysis of a Shunt DC Motor
Example 9-2. A 50-hp, 250-V, 1200 r/min dc shunt motor without compensating windings
has an armature resistance (including the brushes and interpoles) of 0.06 Ω. Its field circuit
has a total resistance RF + Radj of 50 Ω, which produces a no-load speed of 1200 r/min. There
are 1200 turns per pole on the shunt field winding, and the armature reaction produces a
demagnetizing magnetomotive force of 840 A • turns at a load current of 200 A. The
magnetization curve of this machine is shown in Figure .
(a) Find the speed of this motor when its input
current is 200 A.
𝐼 𝐹
∗
= 𝐼 𝐹 −
𝐹𝐴𝑅
𝑁 𝐹
= 5.0𝐴 −
840 𝐴 𝑇𝑢𝑟𝑛𝑠
1200 𝑡𝑢𝑟𝑛𝑠
= 4.3𝐴

19. The Terminal Characteristic of a Shunt DC Motor

20. • THE EQUIVALENT CIRCUIT OFADC MOTOR
• THE MAGNETIZATION CURVE OF A DC
MACHINE
• Type of dc motors
– SEPARATELY EXCITED AND SHUNT DC MOTORS
– THE PERMANENT-MAGNET DC MOTOR
– THE SERIES DC MOTOR
– THE COMPOUNDED DC MOTOR

21. THE SERIES DC MOTOR
)𝑉𝑇 = 𝐼𝐴(𝑅 𝐴 + 𝑅 𝑆
Induced Torque in a Series DC Motor