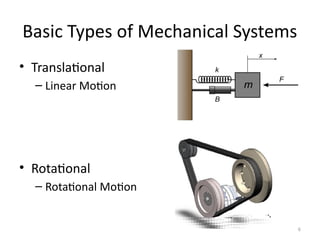
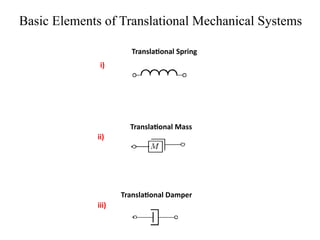
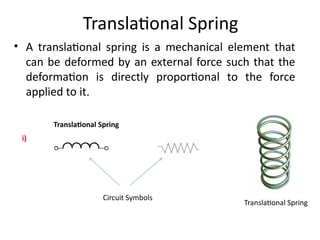
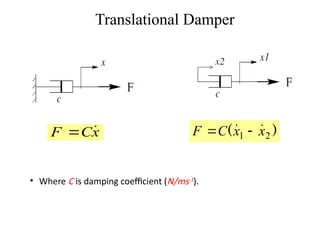
The document discusses mathematical modeling in control system engineering, emphasizing the importance of models for simulation, prediction, and control system design. It differentiates between grey box and white box models based on the knowledge of internal dynamics and highlights basic types of mechanical systems, including translational components such as springs, masses, and dampers. Key equations related to these components are provided, illustrating their behavior under applied forces.

1. Control System Engineering
Mathematical Modelling of Mechanical Systems
Enrollment no:-
130870111005,
130870111016,
130870111017
Guided by:
Asst.Prof. Vishal Shah

2. 2
Model
• A model is a simplified representation or
abstraction of reality.
• Reality is generally too complex to copy exactly.
• Much of the complexity is actually irrelevant in
problem solving.

3. What is Mathematical Model?
A set of mathematical equations (e.g., differential eqs.) that
describes the input-output behavior of a system.
What is a model used for?
• Simulation
• Prediction/Forecasting
• Prognostics/Diagnostics
• Design/Performance Evaluation
• Control System Design

4. 4
Grey Box Model
• When input and output and some information
about the internal dynamics of the system are
known.
• Easier than white box Modelling.
u(t) y(t)
y[u(t), t]

5. 5
White Box Model
• When input and output and internal dynamics
of the system are known.
• One should have complete knowledge of the
system to derive a white box model.
u(t) y(t)
2
2
3
dt
t
y
d
dt
t
du
dt
t
dy )
(
)
(
)
(



6. 6
Basic Types of Mechanical Systems
• Translational
– Linear Motion
• Rotational
– Rotational Motion

7. Basic Elements of Translational Mechanical Systems
Translational Spring
i)
Translational Mass
ii)
Translational Damper
iii)

8. Translational Spring
i)
Circuit Symbols
Translational Spring
• A translational spring is a mechanical element that
can be deformed by an external force such that the
deformation is directly proportional to the force
applied to it.
Translational Spring

9. Translational Spring
• If F is the applied force
• Then is the deformation if
• Or is the deformation.
• The equation of motion is given as
• Where is stiffness of spring expressed in N/m
2
x
1
x
0
2 
x
1
x
)
( 2
1 x
x 
)
( 2
1 x
x
k
F 

k
F
F

10. Translational Mass
Translational Mass
ii)
• Translational Mass is an inertia
element.
• A mechanical system without
mass does not exist.
• If a force F is applied to a mass
and it is displaced to x meters
then the relation b/w force and
displacements is given by
Newton’s law.
M
)
(t
F
)
(t
x
x
M
F 



11. Translational Damper
Translational Damper
iii)
• Damper opposes the rate of
change of motion.
• All the materials exhibit the
property of damping to some
extent.
• If damping in the system is not
enough then extra elements
(e.g. Dashpot) are added to
increase damping.

12. Translational Damper
x
C
F 

• Where C is damping coefficient (N/ms-1).
)
( 2
1 x
x
C
F 
 


13. Example-1
• Consider the following system (friction is negligible)
13
• Free Body Diagram
M
F
k
f
M
f
k
F
x
M
• Where and are force applied by the spring and
inertial force respectively.
k
f M
f

14. 14
Example-1
• Then the differential equation of the system is:
x
M
kx
F 



• Taking the Laplace Transform of both sides and ignoring
initial conditions we get
M
F
k
f
M
f
M
k f
f
F 

)
(
)
(
)
( s
kX
s
X
Ms
s
F 
 2

15. 15
)
(
)
(
)
( s
kX
s
X
Ms
s
F 
 2
• The transfer function of the system is
k
Ms
s
F
s
X

 2
1
)
(
)
(
• if
1
2000
1000



Nm
k
kg
M
2
001
0
2


s
s
F
s
X .
)
(
)
(
Example-1