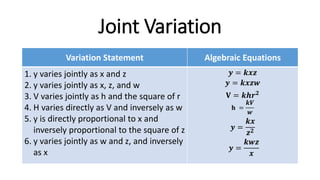
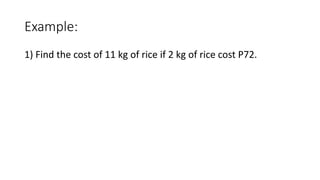This document provides examples and explanations of different types of variation problems involving ratios, proportions, direct variation, inverse variation, and joint variation. It defines key terms like ratio, proportion, direct variation, inverse variation, and joint variation. It shows how to write algebraic equations to represent different variation statements and provides sample problems to practice determining unknown variables based on given variation relationships.

1. Chapter 4
VARIATION

2. Lesson 4.1
RATIO AND PROPORTION
PROBLEMS

3. RATIO
Ratio is a comparison between two quantities. It can be expressed as:
a fraction: 2/3 or as 2:3 read as “2 is to 3”
Examples:
1) There are 8 girls for every 5 boys in grade 9 class.
a. What is the ratio of boys to girls?
b. What is the ratio of girls to boys?
2) There are 10 students for every 5 computers in the computer
laboratory.
a. What is the ratio of students to computers?
b. What is the ratio of computers to students?
5/8 or 5:8
8/5 or 8:5
10/5 or 2:1
5/10 or 1:2

4. Express each of the following as ratio in
simplest form.
1)4 m to 1,800 cm
2)5 days to 1 month
3)21 flowers to 7 vases
4)40 seconds to 1 minute
5)2 days to hours

5. PROPORTION
It is a statement that two ratios are equal.
It can be written in two ways:
A proportion has 4 terms:
2:3 = 4:6 or 2/3 = 4/6
2:3 = 4:6
Means
Extremes
In proportion, the product of the
extremes is equal to the product of
the means.
𝟐
𝟑
=
𝟒
𝟔
ExtremesMeans

6. Examples:
1)
3
4
=
6
𝑛
2)
7
8
=
𝑛
40
3)n : 5 = 2 : 10
4)5 : n = 20 : 28

7. Worded Problems:
1) Mila bought 5 t-shirts for P575. How much will 9 t-shirts
cost?

8. Worded Problems:
2) If Manny is able to plant 120 fruit trees in a week, how
many trees can he plant in 14 days?

9. DIRECT PROPORTIONS
Two quantities are in direct proportion if one quantity
increases (or decreases) in a certain ratio, as the other
quantity increases (or decreases) in the same ratio.
Example:
Three books cost P330.00
Five books cost P550.00

10. Example:
1) Find the cost of 11 kg of rice if 2 kg of rice cost P72.

11. INVERSE PROPORTIONS
Two quantities are in inverse proportion if one quantity
increases (or decreases) in a certain ratio while the other
quantity decreases (or increases) in the inverse of the ratio.
Example:
Ten men painted a house in 4 days.
Five men will paint the same house in 8 days.

12. Example:
1) If 10 boys can do a piece of work in 6 days, how long will it
take 5 boys to do the same work? (assume that all boys are
working at the same rate)

13. Types of
VARIATION

14. Types of Variation
•DIRECT Variation
•INVERSE Variation
•JOINT Variation
“varies directly” or
“directly proportional”
“varies inversely” or
“inversely proportional”
“varies jointly as and inversely as”
or “directly proportional to and
inversely proportional to ”

15. Direct Variation
“y is directly proportional to x”
“y varies directly as x”
y = kx
𝑘 =
𝑦
𝑥

16. CONVERSION: “Variation statements to
Algebraic Equations”
1) a varies directly as b.
2) c is directly proportional to the square of d.
3) r varies directly as the fifth power of s.
4) x varies directly as y.
5) h is directly proportional to (L + W).

17. Sample Problems:
1) If y varies directly as x, and y = 8 when x = 4, find y
when x = 3.

18. Sample Problems:
2) If a varies directly as the square of b, and a = 4 when
b = 3, find a when b = 9.

19. Sample Problems:
3) If r varies directly as the fifth power of s, and r = 16
when s = 2, find r when s = 3.

20. ANSWER
1) If y varies directly as x, and y = 25 when x = 15, find y when x = 8.
2) If y is directly proportional to x, and y = 22 when x = 3, find y when
x = 5.
3) If r varies directly as the cube of s, and r = 8 when s = 2, find r when
s = 5.
4) If r varies directly as the fourth power of s, and r = 12 when s = 2,
find r when s = 3.
5) If (M + 1) varies directly as 𝑁2 and M = 17 when N = 3, find M when
N = 4.

21. Inverse Variation
“y is inversely proportional to x”
“y varies inversely as x”
y =
𝑘
𝑥
𝑘 = 𝑥𝑦

22. CONVERSION: “Variation statements to
Algebraic Equations”
1) a varies inversely as b.
2) c is inversely proportional to the square root of d.
3) m varies inversely as the cube of n.
4) x varies inversely as y.
5) y is inversely proportional to (x – 3).

23. Sample Problems:
1) If y varies inversely as x, and y = 24 when x = 6, find y
when x = 8.

24. Sample Problems:
2) If a varies inversely as the cube root of b, and a = 27
when b = 27, find a when b = 8.

25. Sample Problems:
3) Given that y is inversely proportional to x, and y = 3
when x = 8, find
a) x when y = 6
b) y when x = 2

26. ANSWER
1) If y varies inversely as x, and y = 21 when x = 12, find x when y = 9.
2) If y is inversely proportional to x, and y = 24 when x = 8, find x when
y = 10.
3) Given that M varies inversely as 𝑁2 and M = 48 when N = 3,
calculate:
a) M when N = 4 b) N when M = 8
4) If y varies inversely as (x – 3). If y = 5 when x = 7, find y when x = 5.

27. Joint Variation
Variation Statement Algebraic Equations
1. y varies jointly as x and z
2. y varies jointly as x, z, and w
3. V varies jointly as h and the square of r
4. H varies directly as V and inversely as w
5. y is directly proportional to x and
inversely proportional to the square of z
6. y varies jointly as w and z, and inversely
as x
𝒚 = 𝒌𝒙𝒛
𝒚 = 𝒌𝒙𝒛𝒘
𝐕 = 𝒌𝒉𝒓 𝟐
𝐡 =
𝒌𝑽
𝒘
𝒚 =
𝒌𝒙
𝒛 𝟐
𝒚 =
𝒌𝒘𝒛
𝒙

28. Sample Problems:
1) If z varies jointly as x and y, and z = 24 when x = 2 and y = 4, find z
when x = 2 and y = 5.

29. Sample Problems:
2) If z varies jointly as x and y and z = 12 when x = 2, y =
4, find z when x = 3 and y = 2.

30. Sample Problems:
3) If a varies jointly as b and the square of c, and a = 20
when b =4 and c = 2, find a when b = 2 and c = 4.

31. ANSWER
1) If a varies jointly as c and d, and a = 20 when c = 2
and d = 4, find c when a = 25 and d = 8.
2) If z varies directly as x and inversely as y, and z = 16
when x = 3 and y = 2, find z when x = 5 and y = 3.
3) If z varies directly as the square of x and inversely as
y, and z = 50 when x = 5 and y = 2, find z when x = 4
and y = 5.