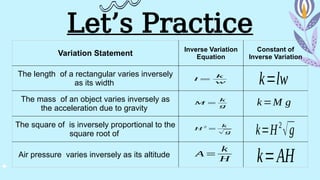
The document outlines the types of variations in mathematics: direct, inverse, joint, and combined variation, providing definitions and equations for each. It explains how each type relates variables to one another, including practical examples for better understanding. Exercises are included to practice translating variation statements into mathematical equations.

1. Translating
Variation
Statements

2. Learning Targets
1. I can illustrates situations that involve
the following variations: (a) direct; (b)
inverse; (c) joint; and (d) combined.
2. I can translate variation statements into
mathematical equations.

3. Definition of
Variation
A variation is a relation between a
set of values of one variable and a
set of values of other variables.

4. Types of Variation
1. Direct Variation
2. Inverse Variation
3. Joint Variation
4. Combined Variation

5. Direct Variation
• As “x” increases, “y” also increases.
• As “x” decreases, “y” also decreases.
Statement: “y varies directly as x”
Key Words: varies directly/directly proportional
Equation: ; where
Example: The fare F of a passenger varies directly as the distance
of d of his destination.
Equation: ; where

6. Let’s Practice
Variation Statement
Direct Variation
Equation
Constant of
Direct Variation
The price per kilo of tomatoes varies directly
as the number of its kilo .
The fare of a passenger varies directly as
the distance of his destination.
The weight of an object is directly
proportional to his mass
The square of is directly proportional to the
square root of
P=kx k =
P
x
F=kd k =
F
d
W =kM k =
W
M
H2
=k √g k =
H 2
√ g

7. Inverse Variation
• As “x” increases, “y” decreases.
• As “x” decreases, “y” increases.
Statement: “y varies inversely as x”
Key Words: varies inversely/inversely proportional
Equation: ; where
Example: The number of pizza slices p varies inversely as the
number of person n sharing a whole pizza.
Equation: ; where

8. Let’s Practice
Variation Statement
Inverse Variation
Equation
Constant of
Inverse Variation
The length of a rectangular varies inversely
as its width
The mass of an object varies inversely as
the acceleration due to gravity
The square of is inversely proportional to the
square root of
Air pressure varies inversely as its altitude
l=
k
w k=lw
M =
k
g k=M g
H
2
=
k
√ g k=H2
√g
A=
k
H k=AH

9. Joint Variation
• A variable varies directly to two or more quantities.
Statement: “y varies jointly as x and z”
Key Word: varies jointly
Equation: ; where
Example: The volume of a cylinder V varies jointly as its height h
and the square of the radius r.
Equation: ; where

10. Let’s Practice
Variation Statement
Joint Variation
Equation
Constant of
Joint Variation
varies jointly as and
The area of a parallelogram varies jointly as
the base and altitude
The volume of a cylinder varies jointly as its
height and the square of the radius
The heat produced by an electric lamp
varies jointly as the resistance and the
square of the current
P=kqr k =
P
qr
A=kbh k =
A
bh
V =khr2 k =
V
h r
2
H =kRI2 k =
H
R I
2

11. Combined Variation
• A variable varies directly to some quantities and
varies inversely to some other quantities.
Statement: “y varies directly as x and varies inversely as z”
Key Word: varies directly + varies inversely
Equation: ; where
Example: The electrical resistance R of a wire varies directly as
its length l and inversely as the square of its diameter d.
Equation: ; where

12. Let’s Practice
Variation Statement
Combined
Variation Equation
Constant of
Combined
Variation
varies jointly as and the square of and
inversely as
varies directly as the square of and
inversely as .
The acceleration of a moving object varies
directly as the distance it travels and
inversely as the square of the time it travels.
W =
kc a2
b
k =
Wb
c a
2
P =
k x2
s
k =
Ps
x
2
A =
kd
t
2 k=
A t2
d

13. Thank you
for
listening! 