This study developed a mathematical model to simulate temperature control of a focal cooling device using a Peltier module on human skin. Experiments using a phantom validated the model, with errors within 1.16% compared to proportional control simulations. Adding integral control improved stability and reduced steady-state error to within 0.45-1.92% of experimental temperatures. Future work will refine model parameters and test new devices to enable precise temperature regulation for medical applications.

1. Study on Temperature Control Model
of the Focal Cooling Human Physiological System
Graduate School of Medicine Yamaguchi University
Kenyu UEHARA
May/20/2015

2. Outline
1. Background
2. Purpose of this study
3. Study method
4. Result and Discussion
5. Conclusion
Introduction of this research

3. Cooling effect has contributed in various fields
Ice (Cryotherapy)
Cooling treatments lower body temperature
in order to relieve pain, swelling,
constriction of blood vessels,
and to decrease the cellular damage
http://kadowakibonesetting.web.fc2.com/cryo.ht
ml
Vasoconstriction
Prevention of Secondary hypoxic injury
• Heat stroke
• Sprain
• Encephalopathy
It was applied to several symptoms
etc.
Background Cooling device
cell
blood
vessels

4. Background Cooling device
Peltier device (Thermoelectric device)
P
N
P
N
P
N
Semiconductor
(P-type & N-type)
Metal plates
Endothermic surface
Exothermic surface
Heat transfer
Peltier device
Lead wire
Thermoelectric coolers operate by the Peltier effect
Advantages
◼ Temperature control
◼ No vibration
◼ Small and Lightweight
For Human body
Medical purposes

5. Peltier device is nonlinear and have uncertainties
Analysis and control of this kind of devices are difficult
◆ Joule heat generated by the input current to the device
◆ Heat conduction in the device inside
<Problems>
Adapting a cooling device,
◆ Thermal conductivity of the heat sink
(To maintain the cooling performance)
◆ Thermal conductivity
of the Cooling object
(Biological reaction caused by cooling)
Heat sink
Peltier device
Cooling water
Human body
(Cooling object)
the entire system
Background Cooling device

6. Mathematical bio-model of the focal cooling device,
In relation to the entire system is a prerequisite
In order to perform a transitional control….
Ambient air
Heat sink
Peltier device
Cooling water
Human body
(Cooling object)
the entire system
Background Cooling device

7. Previous research Modeling
Thermocouple
connectors
Heat sink
Peltier device (6.0×6.0×2.3mm)
Ag plates
Water circulation path
Power supply connector
Coupling connector to the
water circulating system
150mm
Schematic view of the focal cooling device
utilizing the Peltier device
Peltier device is nonlinear and have uncertainties

8. Mathematical model of the amount
of heat of the entire system
Peltier device
Heat sink
Previous research Modeling
We identified the unknown parameters in the mathematical model
solving the inverse problem

9. Mathematical model of the amount
of heat of the entire system
Peltier device
Heat sink
Previous research Modeling
We identified the unknown parameters in the mathematical model
solving the inverse problem

10. In order to minimize the difference
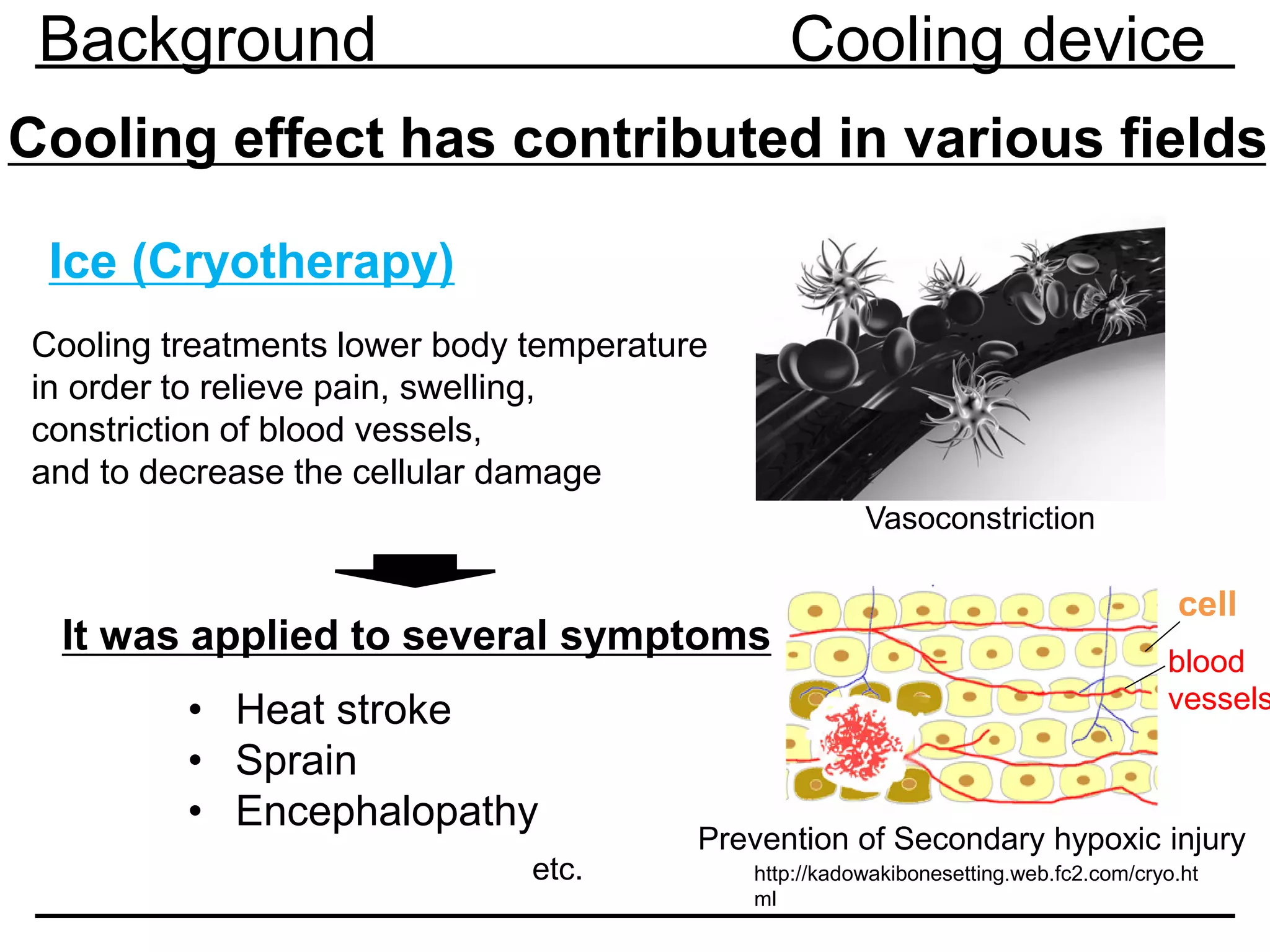
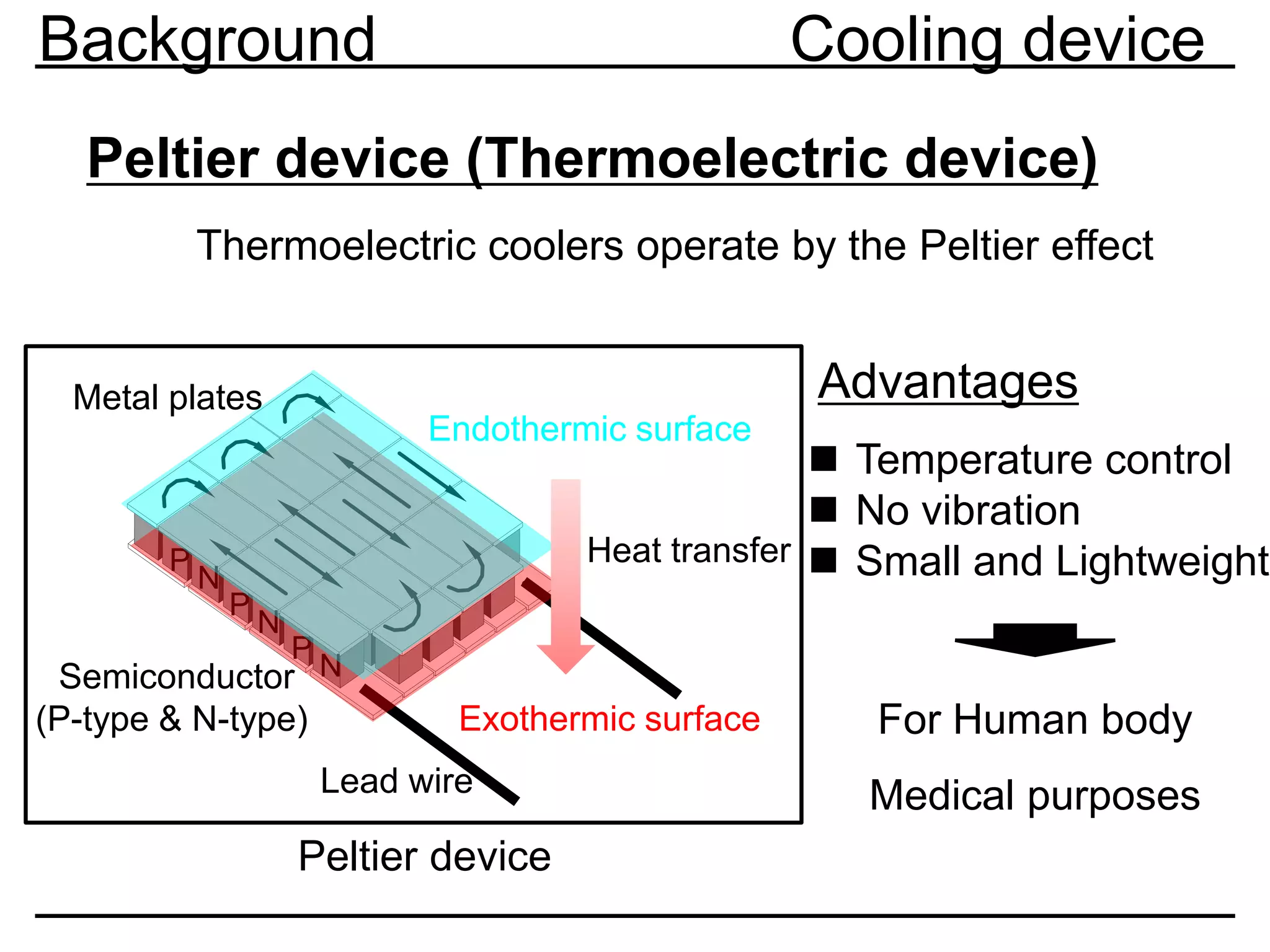
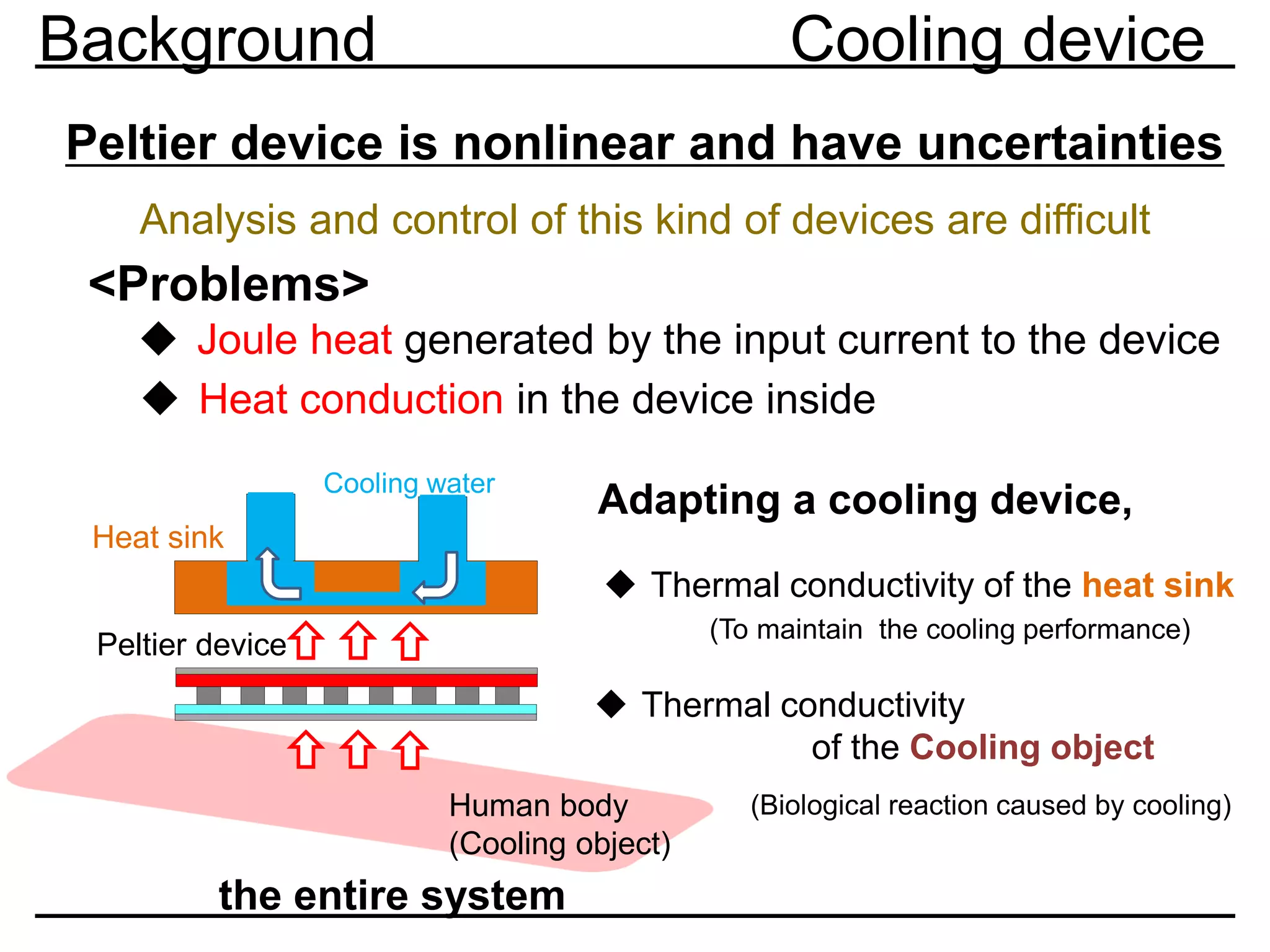
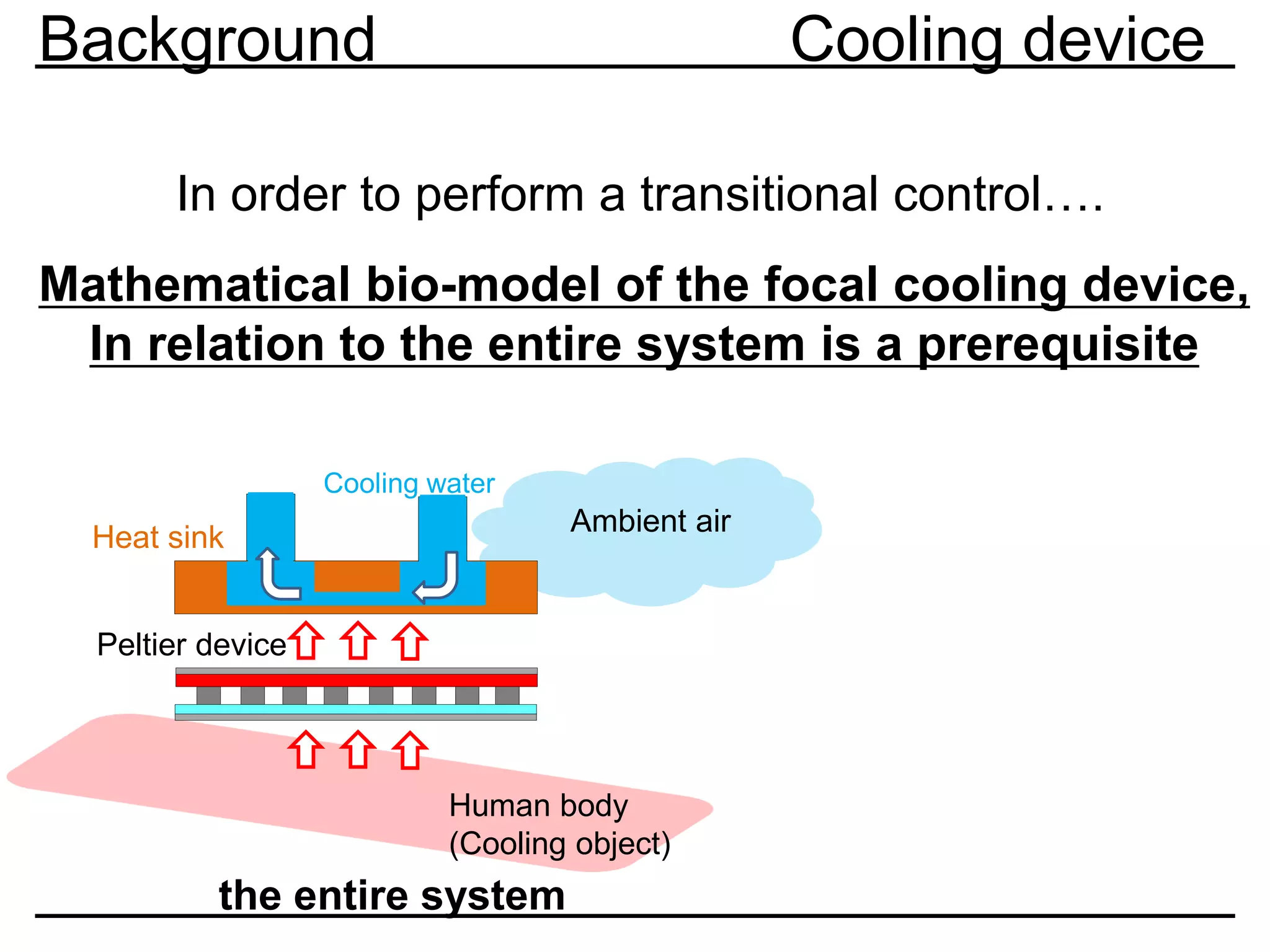
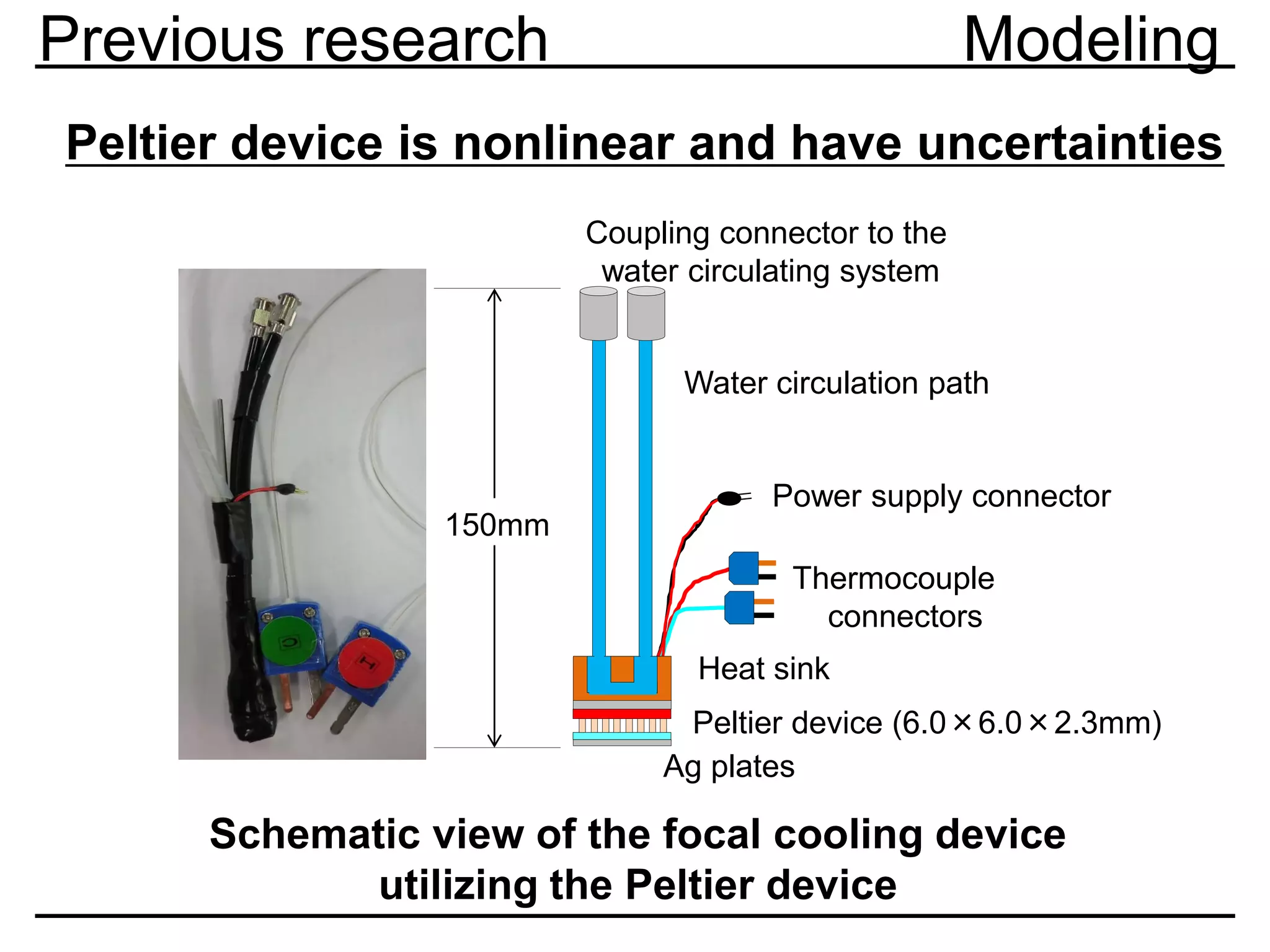
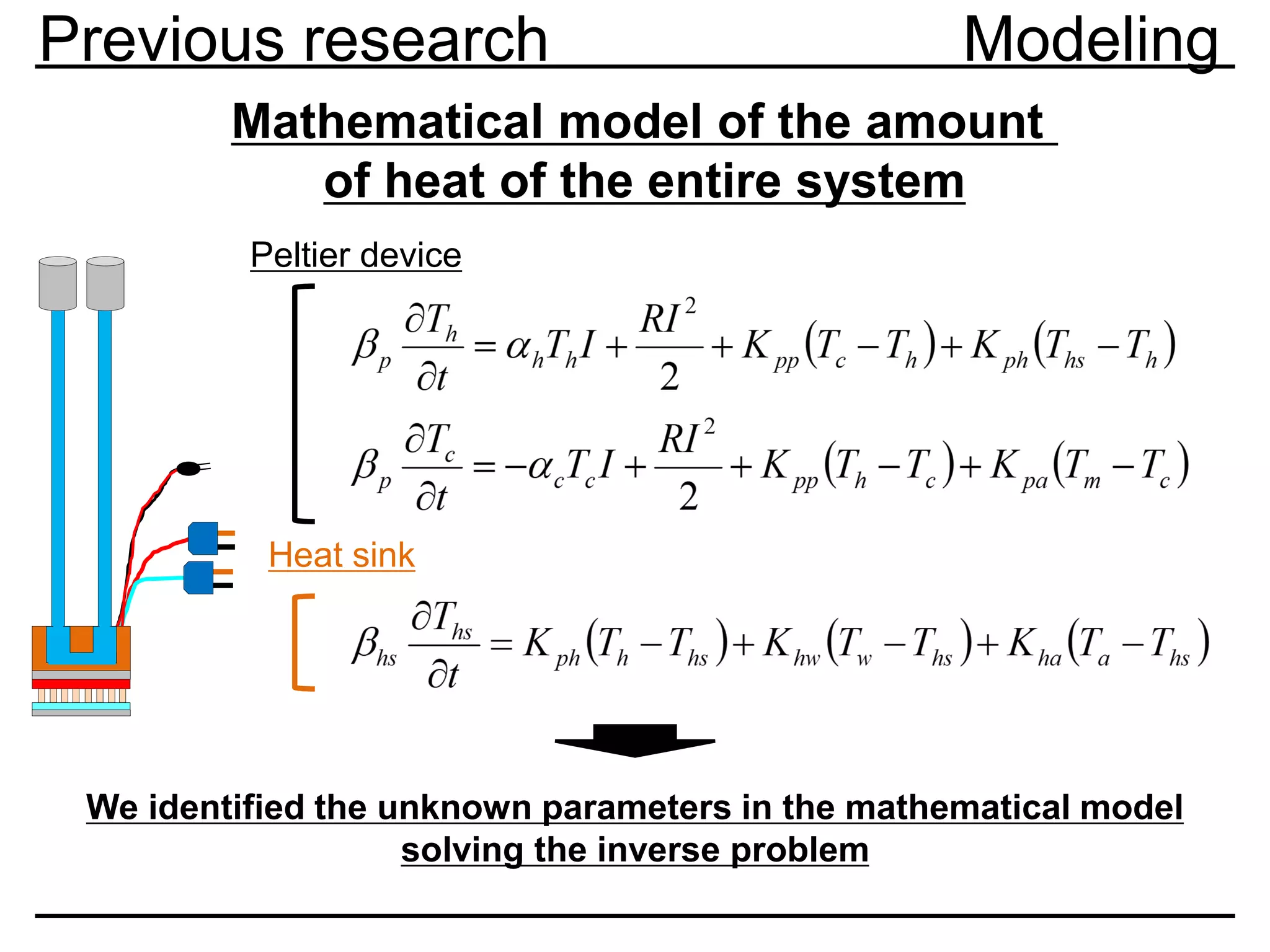
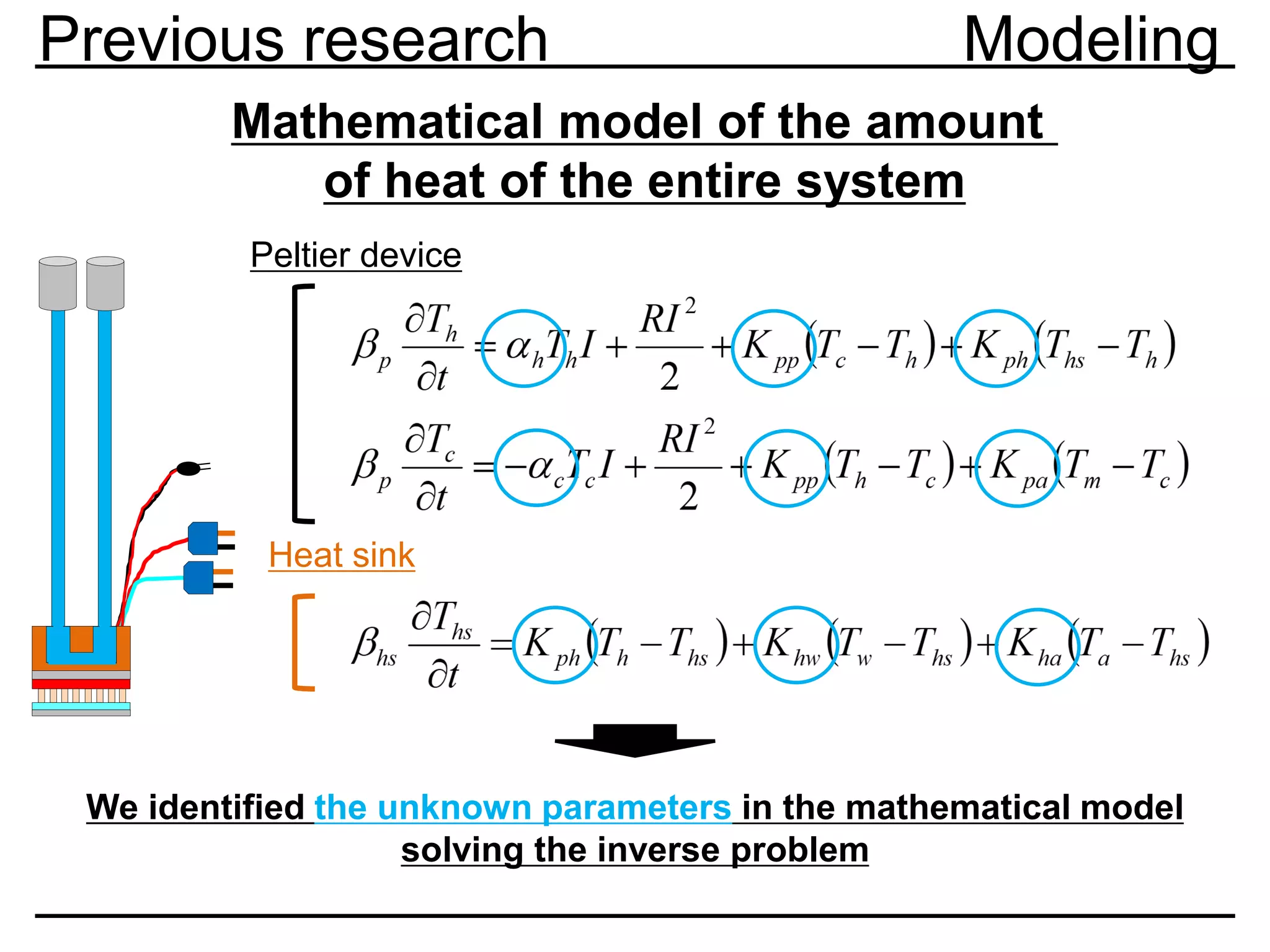
Previous research Modeling
0.0 0.2 0.4 0.6 0.8 1.0 1.2
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
MeanError[%/point]
Input voltage [V]
The relative difference per-point error of the
experimental and simulation value vs. input voltage
1.16 % / point
Average error
Error function
℃
s
Texp.
Tsim.

11. 0 10 20 30 40 50
15
20
25
30
35
40
45
Exp.
Sim.
Temperature[
o
C]
Time [s]
Previous research Modeling
Comparison of the experimental and simulation
results in case of proportional gain Kp is 0.5
Result of the validation of the mathematical model
Proportional control [V]
The relative Error
of the controlled side
1 %/point (0.2～0.3 ℃)
Mathematical model can simulate
Experimental result in the error range
of the parameter identification

12. Previous research Modeling
Comparison of the experimental and simulation
results in case of proportional gain Kp is 0.5
Result of the validation of the mathematical model
Using a temperature control based on ONLY Proportional action
Error in the temperature
of the controlled side
0.2～0.3 ℃
Mathematical model can simulate
Experimental based on the P-control
0 10 20 30 40 50
15
20
25
30
35
40
45
Exp.
Sim.
Temperature[
o
C]
Time [s]
Controlled temperature reaches
a balance away from the target

13. Previous research Modeling
Comparison of the experimental and simulation
results in case of proportional gain Kp is 0.5
Using a temperature control based on ONLY Proportional action
Error in the temperature
of the controlled side
0.2～0.3 ℃
Mathematical model can simulate
Experimental based on the P-control
0 10 20 30 40 50
15
20
25
30
35
40
45
Exp.
Sim.
Temperature[
o
C]
Time [s]
Controlled temperature reaches
a balance away from the target
General temperature control.
⚫ To eliminate the steady-state error
⚫ To improve the stability of the system
In order to adapt to a living body,
accuracy of the cooling temperature is an important factor
PI,PD, or PID control
P : Proportional action
I : Integral action
D : Derivative action
Is used as needed in the temperature control

14. To establish a mathematical model,
which enables temperature control simulation
based on the PI control
➢Evaluation of the mathematical model
1. Experimental equipment & condition
2. Result of the experiment and simulation
3. Discussion
Purpose

15. Evaluation of the model Exp. Set-up
Thermocouple
Conductor wire
Water line
IN OUT
Temperature Controlled Bath
Pump
PLC
PC
Power Amp
Phantom
(Vegetable gelatin)
Focal cooling
device
Schematic of the experimental set-up
• Phantom
Vegetable gelatin
• Sampling time
50 ms
• Control period
500 ms
• Temperature resolution
0.1 ℃
• Ambient temperature
25.0 ℃
• Phantom temperature
37.0 ℃
• Measurement time
180 sec
Experimental equipment

16. PI control
[V]
Input voltage
25
32 ~ 33
Time [s]
Temperature [℃]
Cooling start Cooling end
10 50
Heat side
Cool side
controlled
Evaluation of the model Exp.& Sim.
Proportional gain Integral gainControl error
(0.5) 15.0
30.0
50.0
Condition of the experiment and simulation

17. 0 10 20 30 40 50
15
20
25
30
35
40
45
Exp.
Sim.
Temperature[
o
C]
Time [s]
An example of result in case of proportional
gain is 0.5 and integral gain is 15.0
Ki Controlled side Both sides
15.0 0.66 1.92
30.0 0.24 1.23
50.0 0.45 1.48
Relative error per-point of the results [%/point]
The average error in the parameter
identification is 1.16%/point
The relative error in the both sides is nearly equal
to the time of the parameter identification
It is to be sufficiently possible simulated in the error
range at the time of the parameter identification
Evaluation Result & discussion

18. Conclusion & work plan PI control
It is shown that the one can simulate results
in the range of the parameter identification
To establish a mathematical model,
which enables temperature control simulation
based on the PI control
We performed cooling control experiment and simulation
Work plan
• Reviewing of the parameters
• Parameter identification of the new device