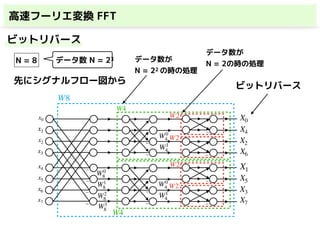
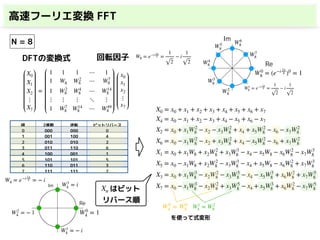
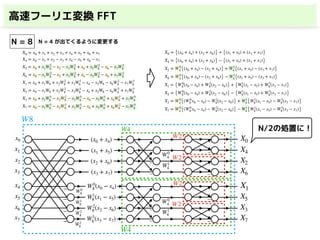
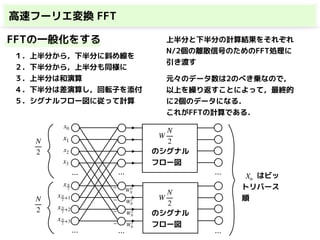
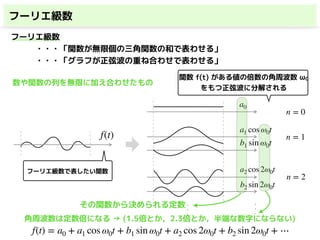
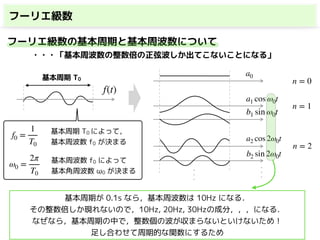
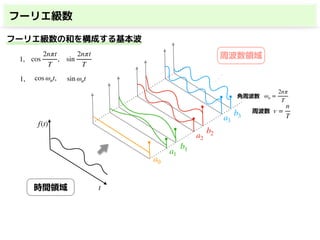
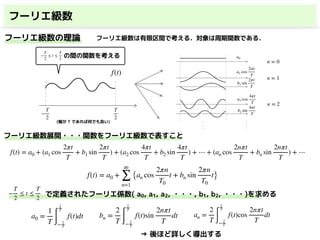
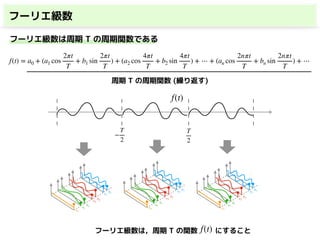
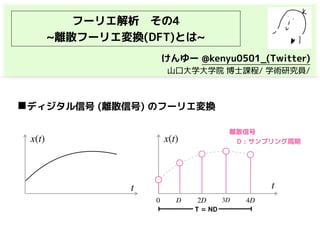
このスライドでは,
・フーリエ級数
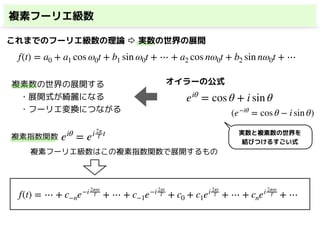
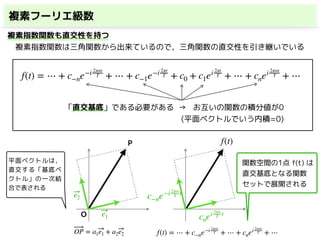
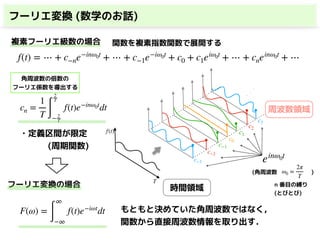
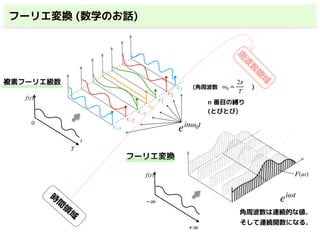
・複素フーリエ級数
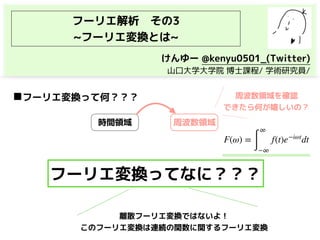
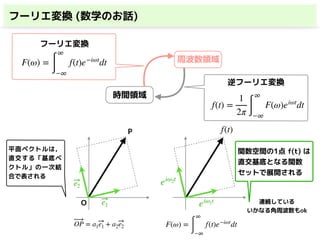
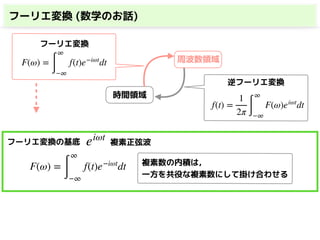
・フーリエ変換(連続)
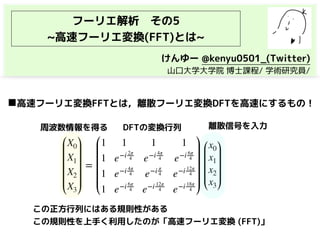
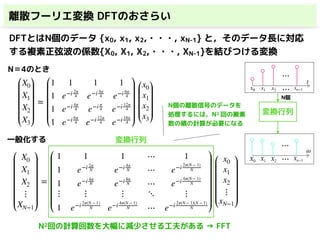
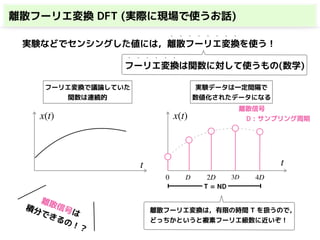
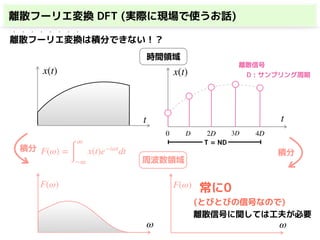
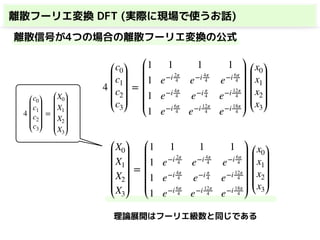
・離散フーリエ変換(DFT)
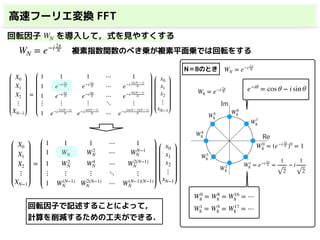
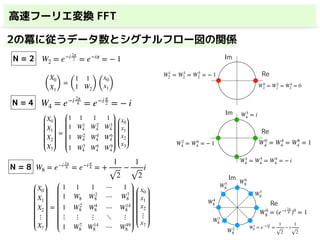
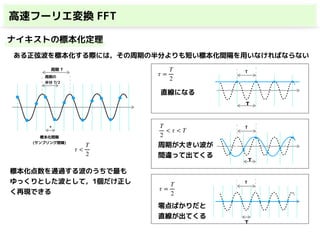
・高速フーリエ変換(FFT)
を解説しています.
ブログはこちら
【フーリエ解析05】高速フーリエ変換(FFT)とは?内側のアルゴリズムを解説!【解説動画付き】
https://kenyu-life.com/2019/07/08/what_is_fft/
Twitter → https://twitter.com/kenyu0501_?lang=ja
Youtube → https://youtu.be/zWkQX58nXiw




![フーリエ級数
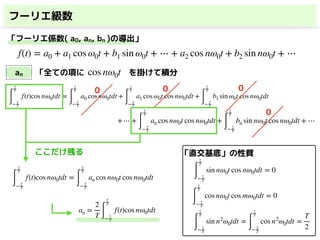
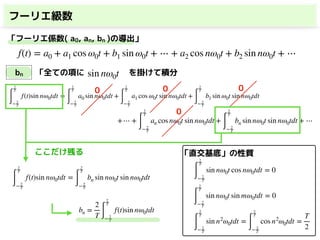
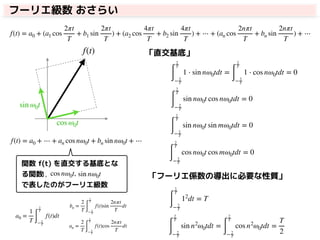
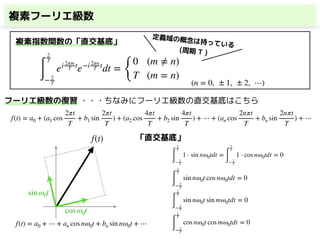
「フーリエ係数( a0, an, bn )の導出」
cos nω0t, sin nω0t
a0 「全ての項に1を掛けて積分」 → 直交基底の性質(積分値=0)から導出できる
∫
2
T
− 2
T
f(t)dt =
∫
2
T
− 2
T
a0dt +
∫
2
T
− 2
T
a1 cos ω0tdt +
∫
2
T
− 2
T
b1 sin ω0tdt + ⋯ +
∫
2
T
− 2
T
an cos nω0tdt +
∫
2
T
− 2
T
bn sin nω0tdt + ⋯
∫
2
T
− 2
T
1 ⋅ sin nω0tdt =
∫
2
T
− 2
T
1 ⋅ cos nω0tdt = 0
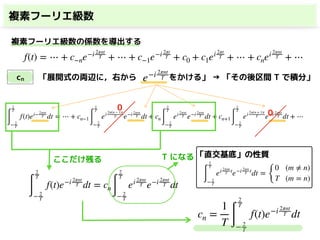
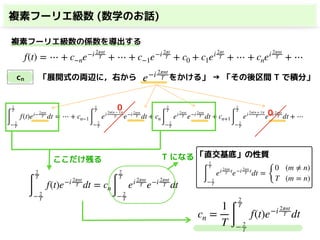
「直交基底」の性質ここだけ残る
∫
2
T
− 2
T
f(t)dt = a0[t]
2
T
− 2
T
a0 =
1
T ∫
2
T
− 2
T
f(t)dt
0 0 0 0
同様に an, bn も,それぞれ導出できる
f(t) = a0 + a1 cos ω0t + b1 sin ω0t + ⋯ + a2 cos nω0t + b2 sin nω0t + ⋯
を全体に掛けて積分](https://image.slidesharecdn.com/20190527fftforslideshare-190708163842/85/slide-15-320.jpg)






![高速フーリエ変換 FFTへの誘い...
X0
X1
X2
X3
=
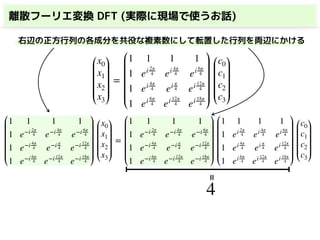
1 1 1 1
1 −i −1 i
1 −1 1 −1
1 i −1 −i
x0
x1
x2
x3
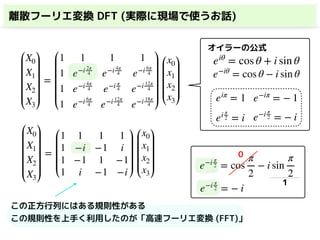
◼オイラーの公式により書き直す オイラーの公式
eiθ
= cos θ + i sin θ
e−iθ
= cos θ − i sin θ
e−i π
2 = − iei π
2 = i
eiπ
= 1 e−iπ
= − 1
X0
X2
X1
X3
=
1 1 1 1
1 −1 1 −1
1 −i −1 i
1 i −1 −i
x0
x1
x2
x3
2行目と3行目を入れ替える
E1 =
[
1 1
1 −i]
E2 =
[
1 −i
1 i ]
−E2
[
E1 E1
E2 −E2]
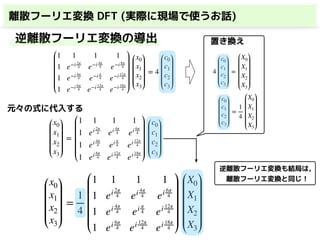
DFTの変換行列が
簡単に表される
このような感じで...](https://image.slidesharecdn.com/20190527fftforslideshare-190708163842/85/slide-46-320.jpg)