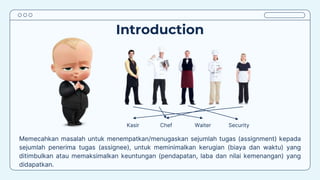
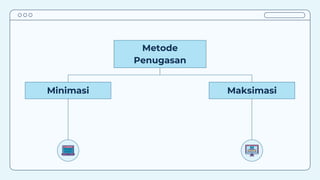
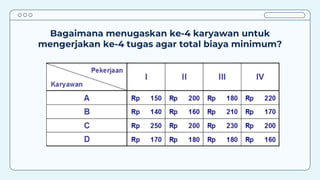
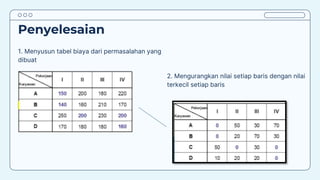
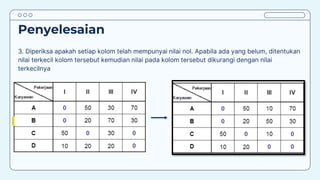
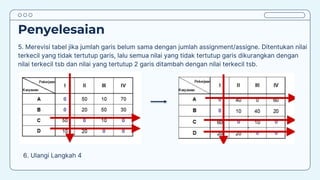
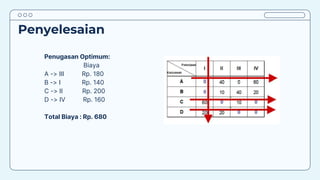
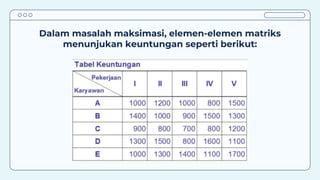
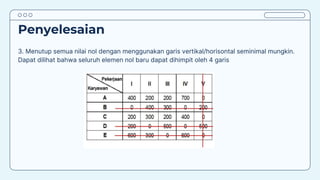
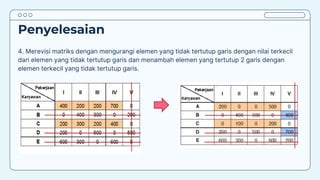
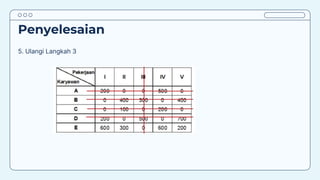
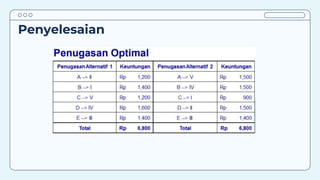
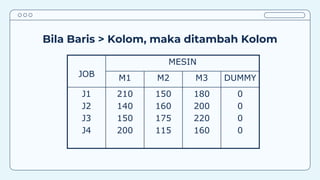
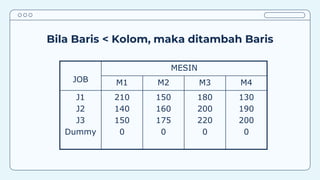
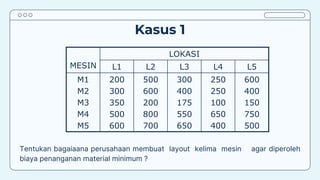
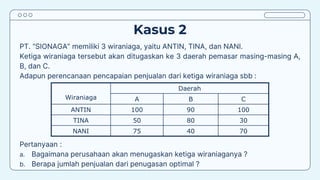
Teks tersebut membahas tentang metode penugasan (assignment problem) untuk mengalokasikan sumber daya terbatas secara optimal. Metode ini digunakan untuk meminimalkan biaya atau memaksimalkan keuntungan dengan menugaskan pekerjaan kepada karyawan/mesin berdasarkan biaya/keuntungan yang dihasilkan. Contoh kasus membahas tentang penugasan karyawan untuk pekerjaan dan penentuan lokasi mesin untuk menangani material agar diperoleh