Merge sort splits the list into halves, recursively sorts each half, and then merges the sorted halves back together into a single sorted list. It has three steps: 1) split the list into halves, 2) recursively sort the halves, and 3) merge the sorted halves back together. It is an efficient O(n log n) sorting algorithm that requires additional space for the two halves during splitting.

1. MERGE SORT
The merge sort splits the list to be sorted into two equal halves, and places them in
separate arrays. Each array is recursively sorted, and then merged back together to
form the final sorted list.
Aim:
Write a program to Sort values in Ascending or Descending Order using
Merge Sort Technique in Linear Array.
Theory:
Merge sort is a recursive algorithm that continually splits a list in half. If the list is
empty or has one item, it is sorted by definition (the base case). If the list has more
than one item, we split the list and recursively invoke a merge sort on both halves.
Once the two halves are sorted, the fundamental operation, called a merge, is
performed. Merging is the process of taking two smaller sorted lists and combining
them together into a single, sorted, new list. Figure 1 shows our familiar example list
as it is being split by merge Sort. Figure 2 shows the simple lists, now sorted, as
they are merged back together
In order to analyse the merge sort function, we need to consider the two distinct
processes that make up its implementation. First, the list is split into halves. We
already computed (in a binary search) that we can divide a list in half log n times
where n is the length of the list. The second process is the merge. Each item in the
list will eventually be processed and placed on the sorted list. So the merge
operation which results in a list of size n requires n operations. The result of this
analysis is that log n splits, each of which costs n for a total of n log n operations. A
merge sort is an O (n log n) O (n log n) algorithm.
Recall that the slicing operator is O(k)O(k) where k is the size of the slice. In order to
guarantee that merge Sort will be O (n log n) O (n log n) we will need to remove the
slice operator. Again, this is possible if we simply pass the starting and ending
indices along with the list when we make the recursive call. We leave this as an
exercise.
It is important to notice that the merge Sort function requires extra space to hold the
two halves as they are extracted with the slicing operations. This additional space
can be a critical factor if the list is large and can make this sort problematic when
working on large data sets.
Name
Reg #
Grade

2. Figure 1
Figure 2
Splitting [54, 26, 93, 17, 77, 31, 44, 55, 20]
Splitting [54, 26, 93, 17]
Splitting [54, 26]
Splitting [54]
Merging [54]
Splitting [26]

3. Merging [26]
Merging [26, 54]
Splitting [93, 17]
Splitting [93]
Merging [93]
Splitting [17]
Merging [17]
Merging [17, 93]
Merging [17, 26, 54, 93]
Splitting [77, 31, 44, 55, 20]
Splitting [77, 31]
Splitting [77]
Merging [77]
Splitting [31]
Merging [31]
Merging [31, 77]
Splitting [44, 55, 20]
Splitting [44]
Merging [44]
Splitting [55, 20]
Splitting [55]
Merging [55]
Splitting [20]
Merging [20]
Merging [20, 55]
Merging [20, 44, 55]
Merging [20, 31, 44, 55, 77]
Merging [17, 20, 26, 31, 44, 54, 55, 77, 93]
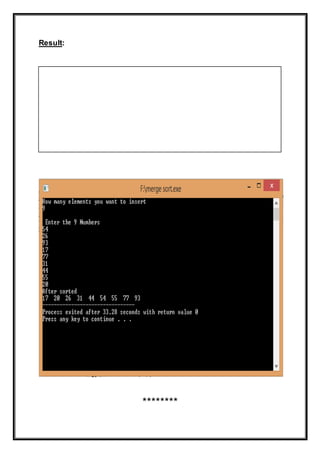
[17, 20, 26, 31, 44, 54, 55, 77, 93]
Algorithm: MERGESORT (A, N)
1. If N=1, Return.
2. Set N1: =N/2, N2: =N-N1
3. Repeat for i=0,1,2,3 . . . (N1-1)
Set L[ i ]=A[ i ].
4. Repeat for j=0,1,2,3 . . . (N2-1)
Set R[ j ]=A[N1+j].
5. CALL MERGE SORT (L, N1).
6. CALL MERGE SORT (R, N2).
7. CALL MERGE (A,L,N1,R,N2).
8. Return.
Algorithm: MERGE (A,L,N1,R,N2)
1. Set i:=0, j:=0.
2. Repeat for k=0,1,2 . . . (N1+N2-1)
If i<n1, then:
If j=N2 or L[ i ] ≤ R [ j ], then:
Set A [k] = L[ i ].
Set i=i+1;

4. Else:
If j<N2, then:
Set A [k] = R [ j ].
Set j=j+1.
3. Return.
Code:

5. Result:
********