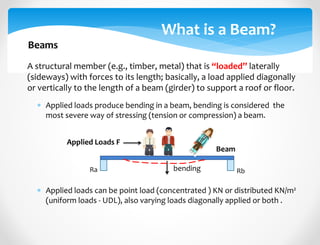
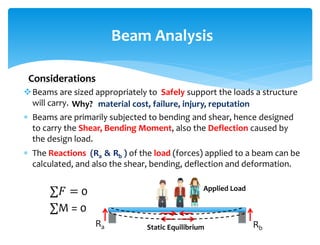
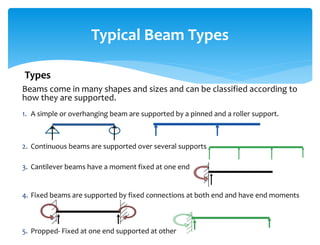
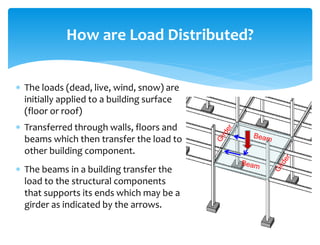
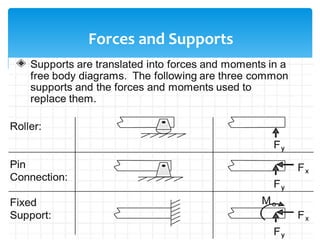
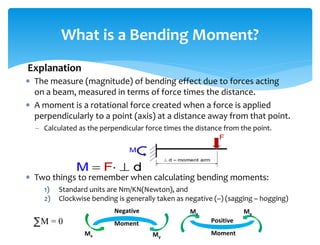
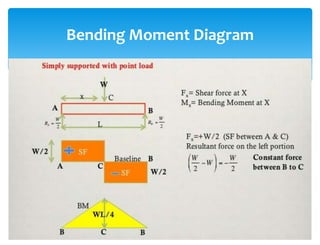
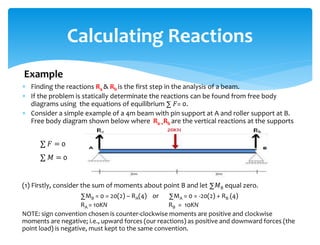
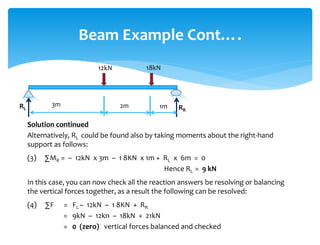
The document discusses calculating reactions to loads applied to beams. It begins by defining key terms like beams, loads, forces, and equilibrium. It explains that reactions must be calculated to balance applied loads and achieve static equilibrium. The document then provides examples of calculating reactions on simple beams using free body diagrams and the principles of moment and force equilibrium. Reactions are found by taking moments and forces around supports and setting equations equal to zero.