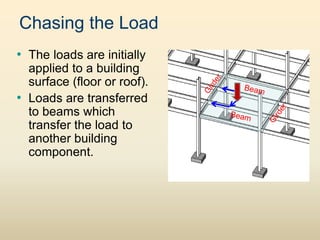
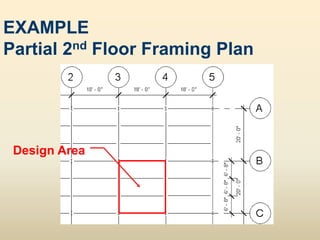
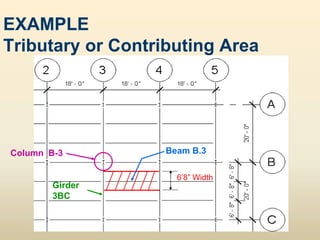
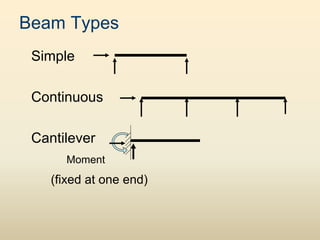
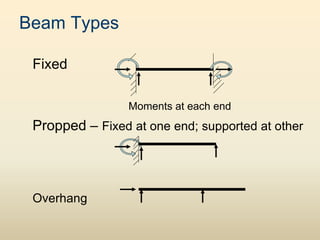
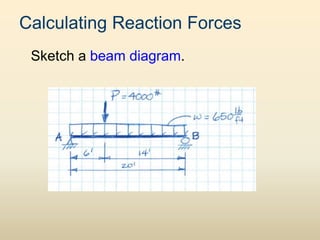
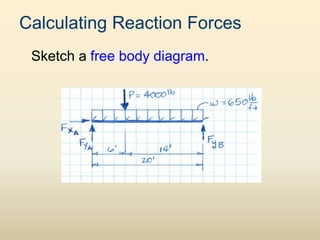
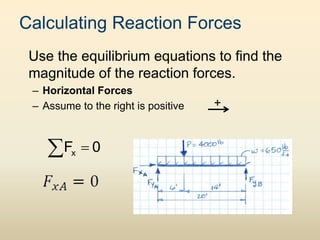
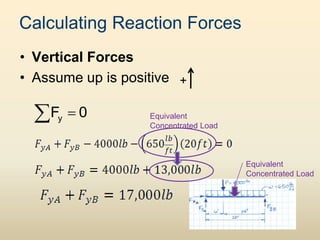
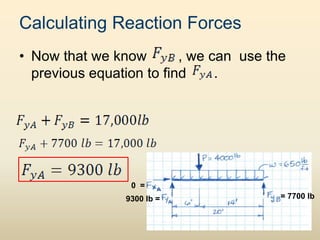
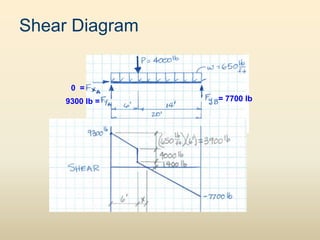
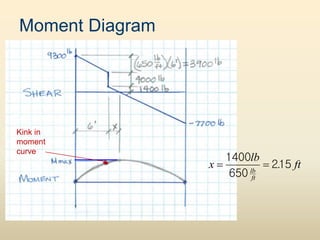
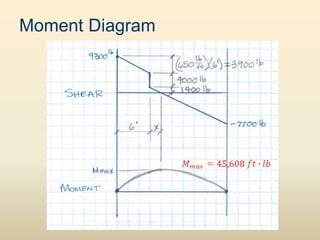
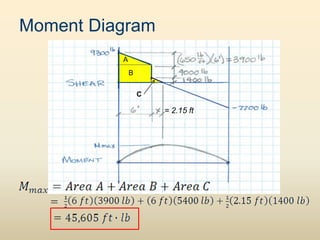
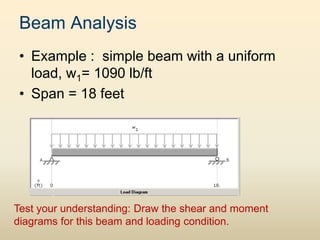
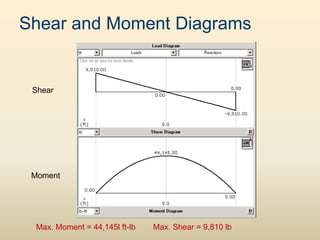
The document discusses beam analysis and design. Beams are structural members that carry loads applied transverse to their length, such as floor or roof loads, and transfer these loads to other structural components. Beams must be in static equilibrium, with reaction forces at supports balancing the applied loads, to successfully carry loads. The types of beams include simple, continuous, and cantilever beams. Beam analysis involves drawing beam diagrams, free body diagrams, and using equilibrium equations to calculate the reaction forces, shear forces, and bending moments in the beam.