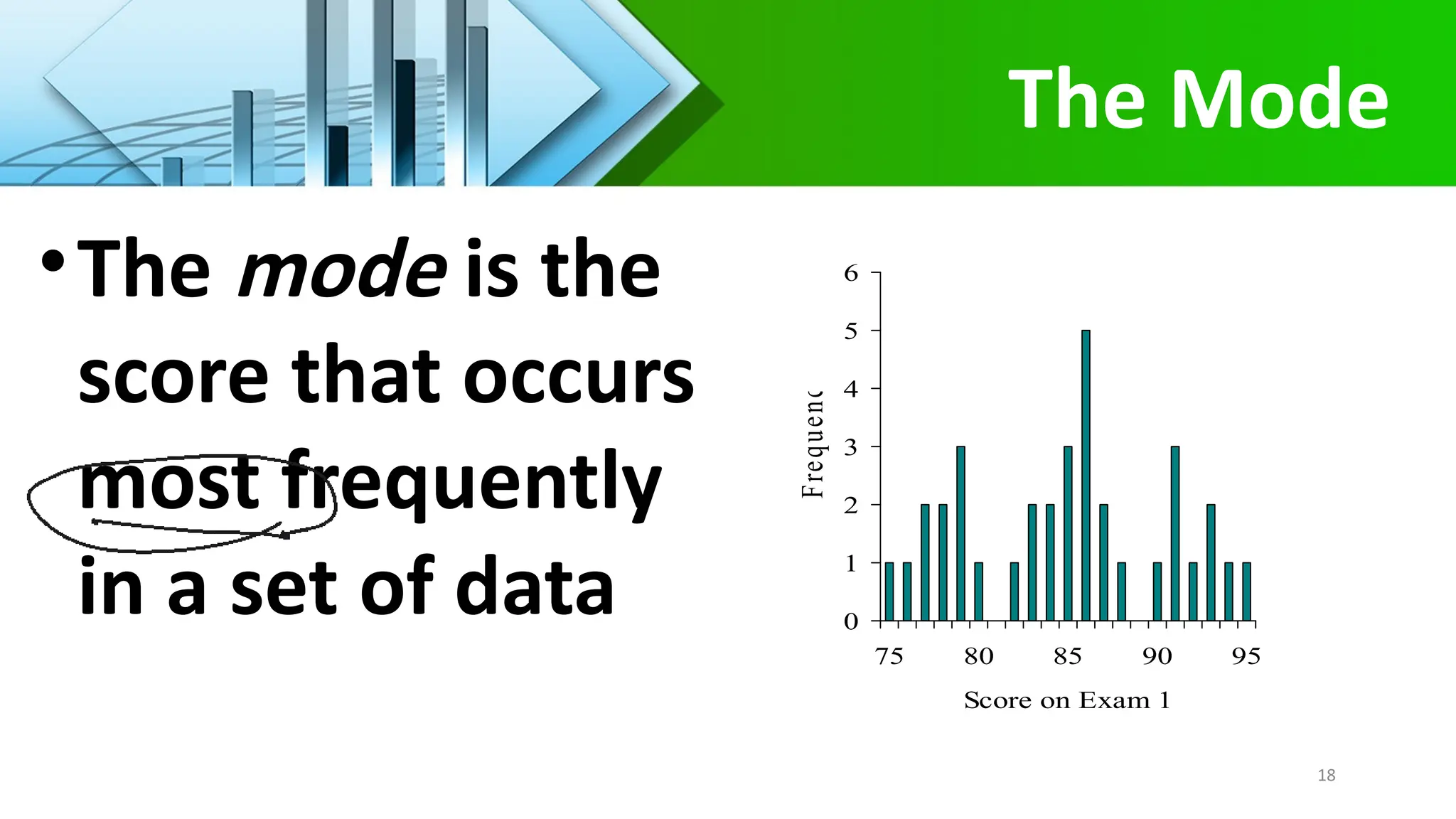
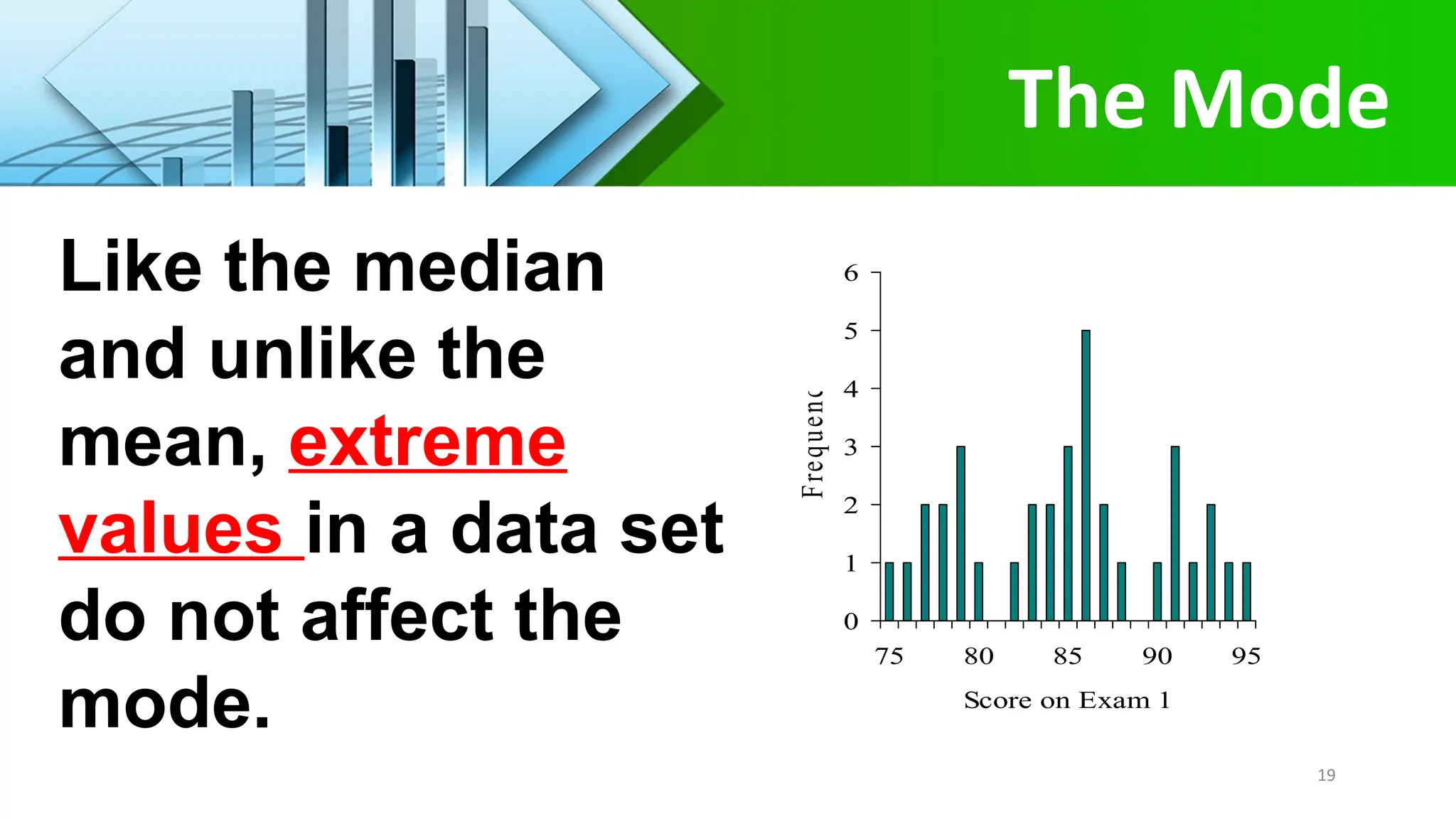
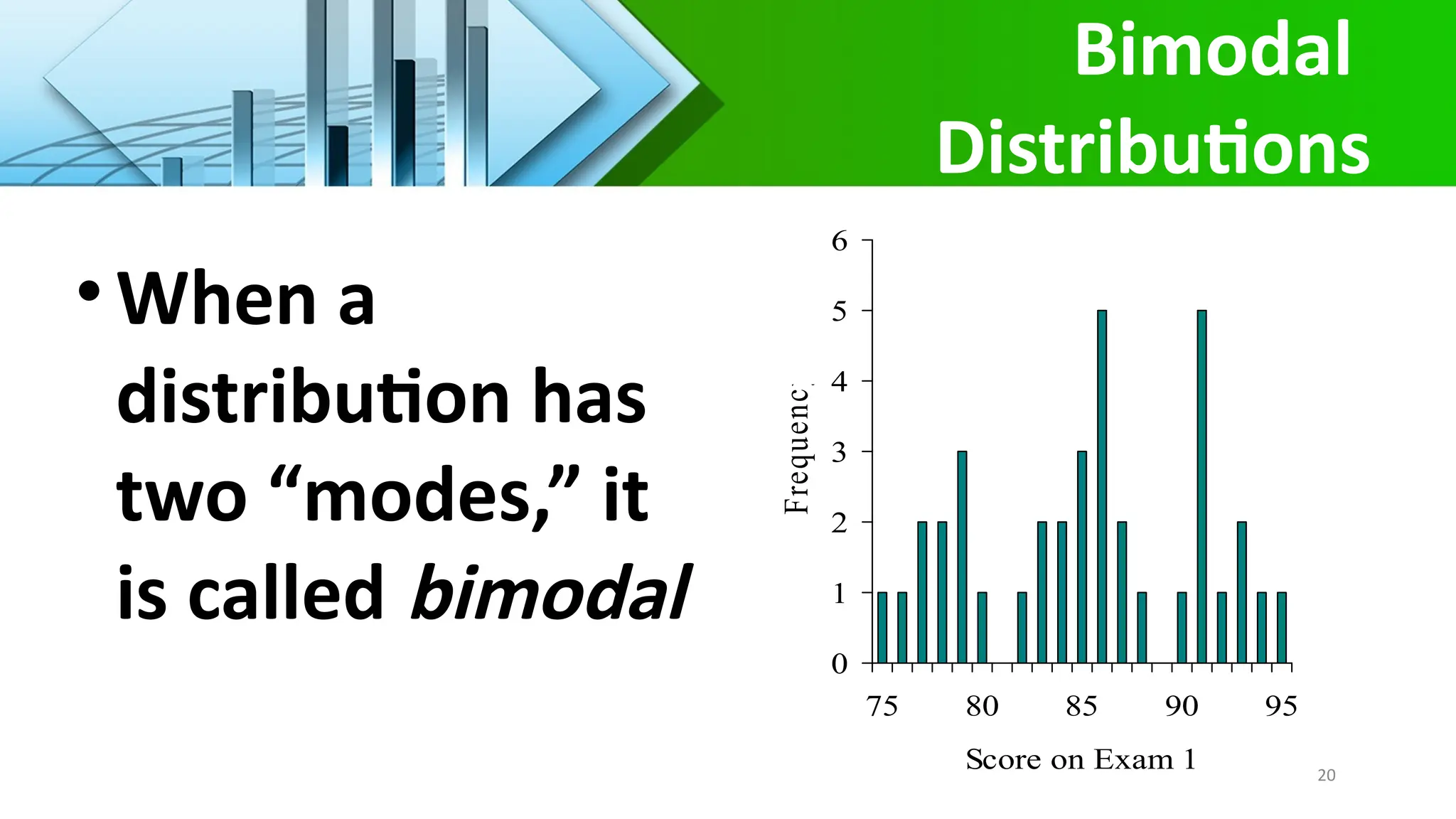
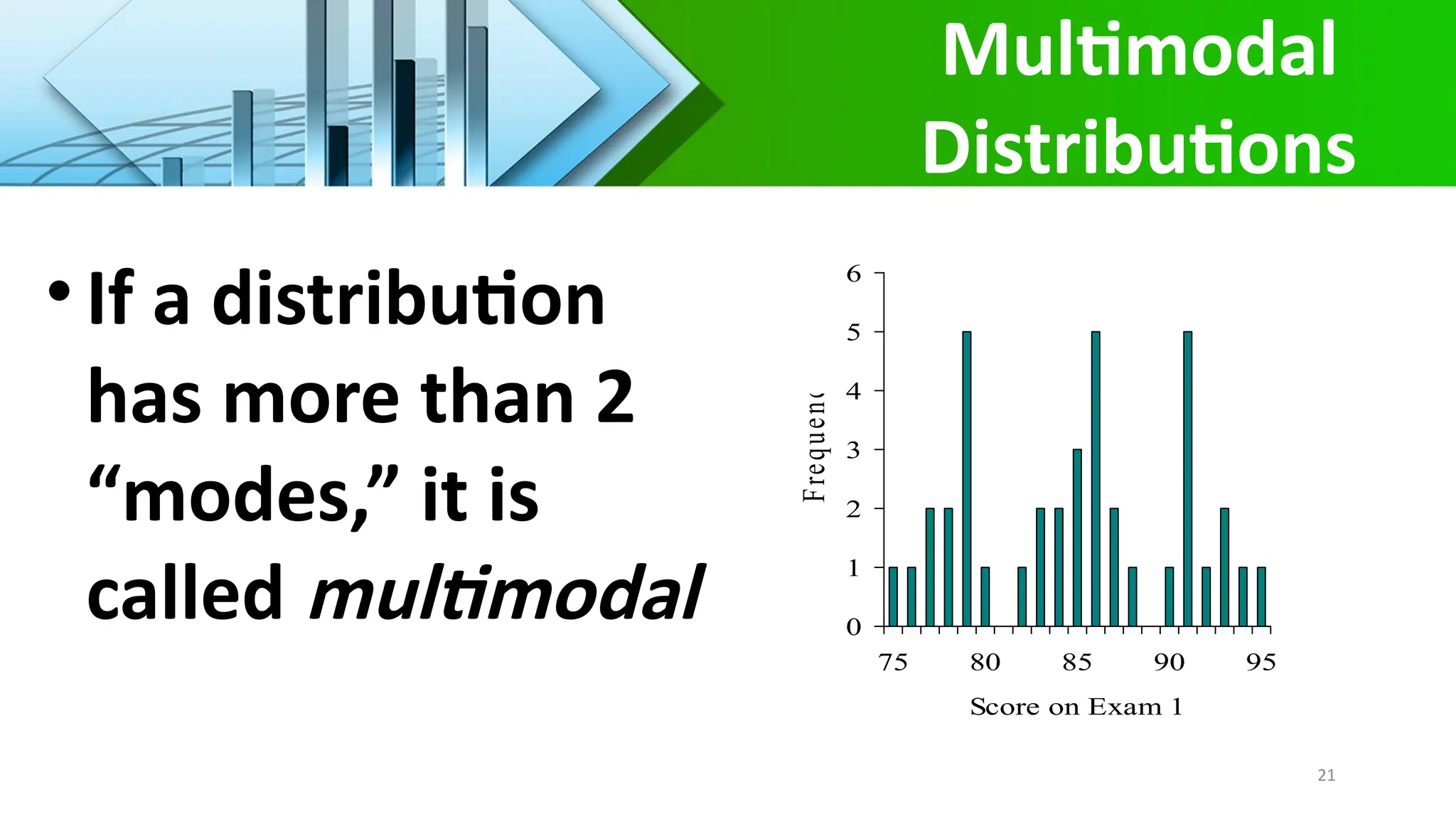
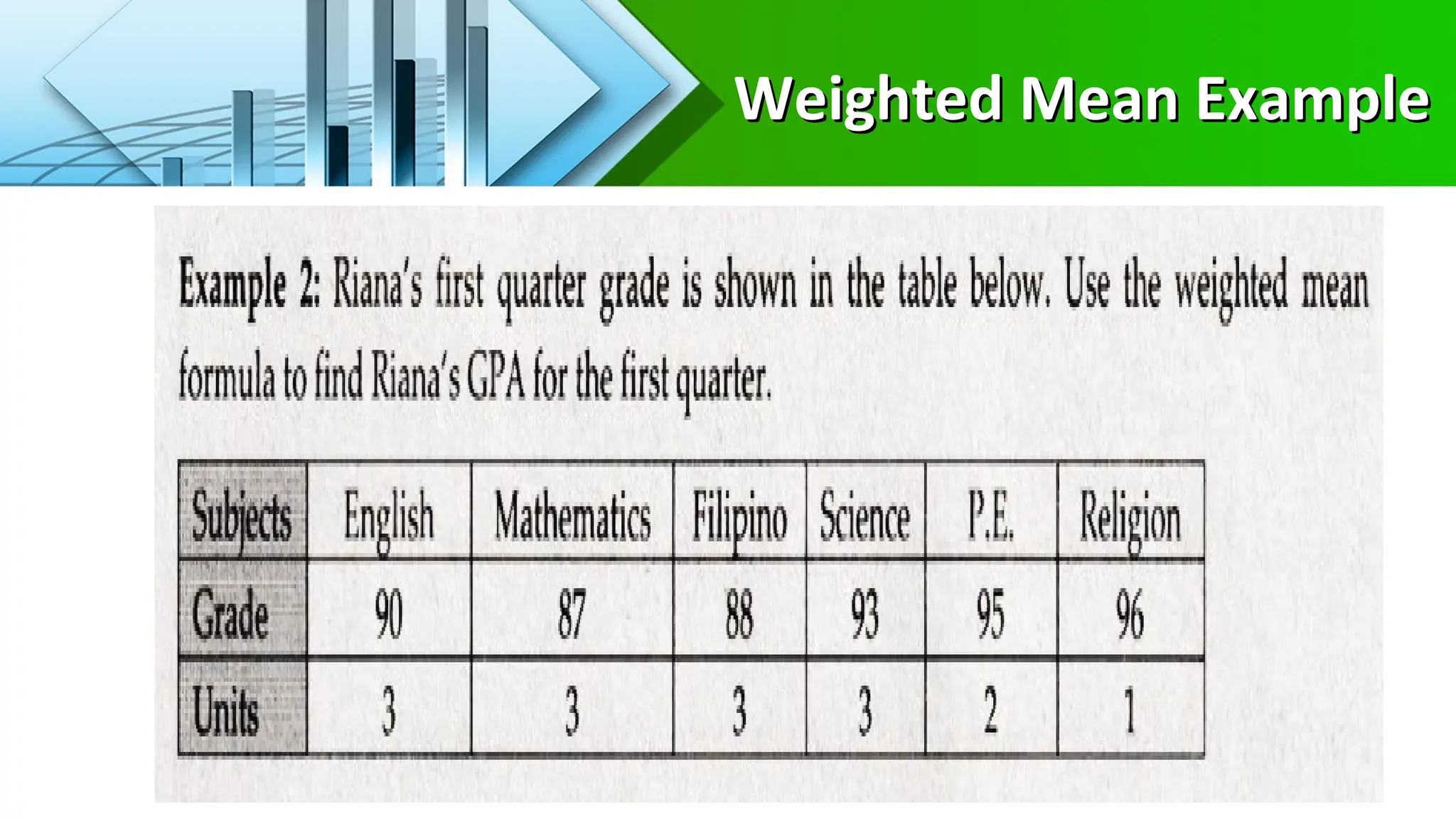
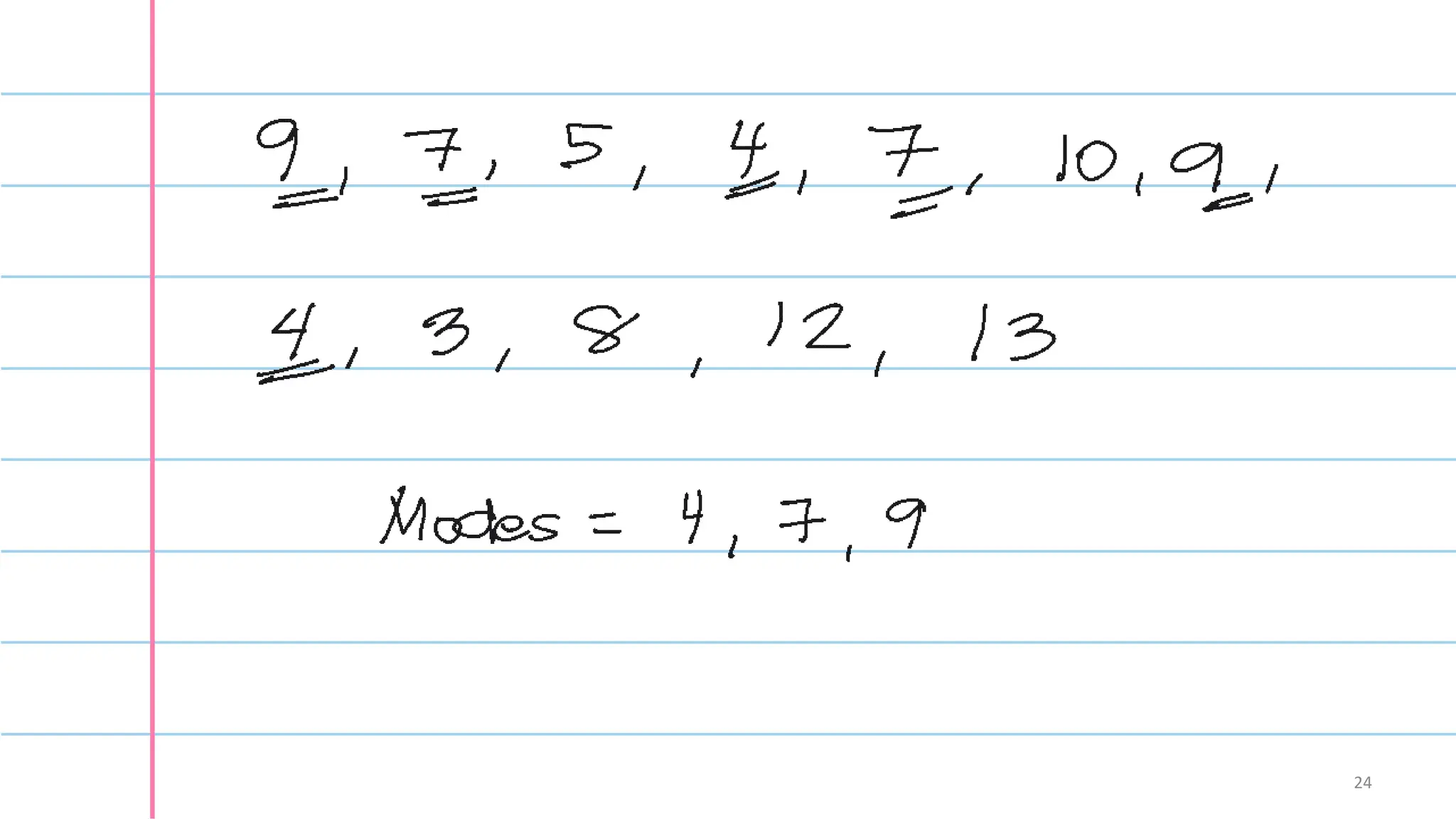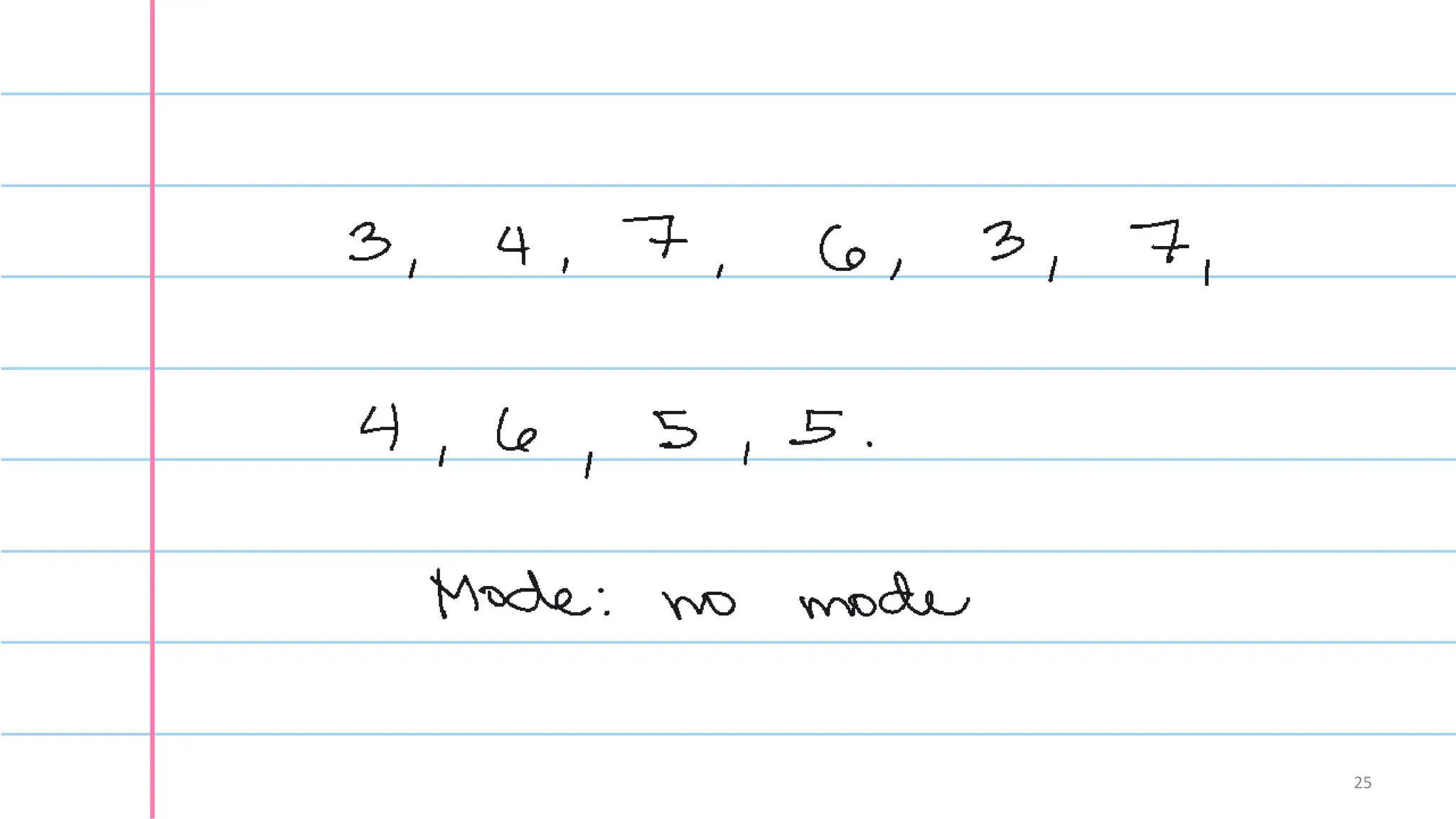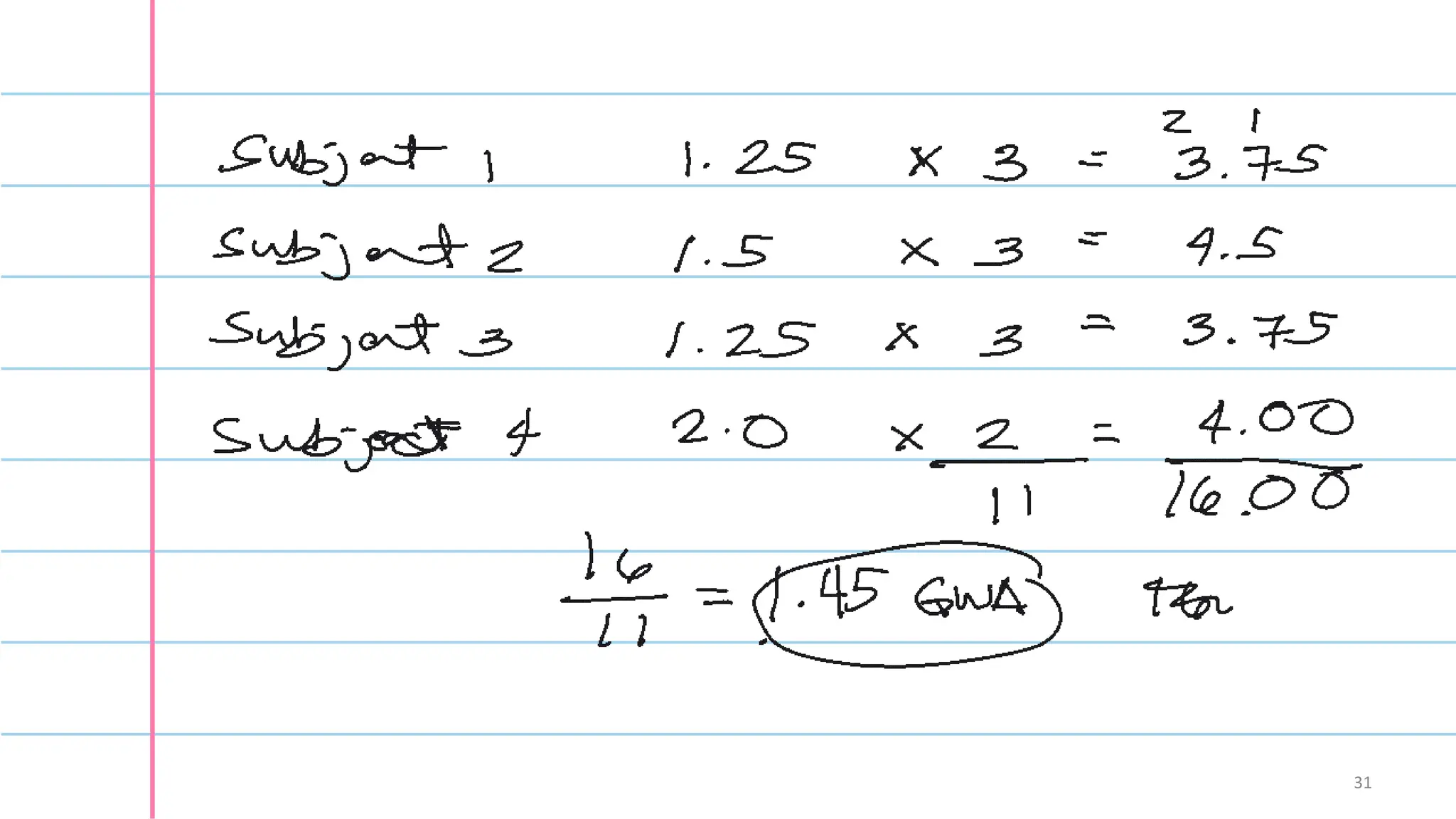The document explains measures of central tendency, focusing on the mean, median, and mode. It details how to calculate these statistics, when to use each, and their respective properties. Furthermore, it discusses the relationships between distributions and the concept of a weighted mean.

1. 1
MEASURES
OF
CENTRAL TENDENCY

2. Measures of Central Tendency
Measures of Central Tendency
• A measure of central tendency is a descriptive statistic
that describes the average, or typical value of a set of
scores
• There are three common measures of central
tendency:
–the mode
–the median
–the mean
2

3. The Mean
The Mean
3
The arithmetic mean, often called as the mean,
is the most frequently used measure of central
tendency.
The mean is the only common measure in which
all values play an equal role, meaning, to
determine its values you would need to consider
all the values of any given data set.

4. The Mean
The Mean
4
The mean is appropriate to determine the
central tendency of an interval or ratio data.
The symbol x̄,, called "xbar," is used to
represent the mean of a sample and the symbol
µ, called “mu", is used to denote the mean of a
population.

5. Properties of Mean
Properties of Mean
5
1.A set of data has only one mean.
2. Mean can be applied for interval and ratio
data.
3. All values in the data set are included in
computing the mean.

6. Properties of Mean
Properties of Mean
6
4. The mean is very useful in comparing two
or more data sets.
5. Mean is affected by the extreme small or
large values on a data set,
6. Mean is most appropriate in symmetrical
data.

7. The Mean
The Mean
7
The mean for ungrouped data is obtained by dividing the sum of all values by
the number of values in the data set. Thus,
Mean for population data:
Mean for sample data:
where is the sum of all values; N is the population size; n is the sample
size; is the population mean; and is the sample mean.
N
x



n
x
x


 x
 x

8. Calculating the Mean
Calculating the Mean
• Calculate the mean of the following data:
1 5 4 3 2
• Sum the scores (X):
1 + 5 + 4 + 3 + 2 = 15
• Divide the sum (X = 15) by the number of scores (N = 5):
15 / 5 = 3
• Mean = X = 3
8

9. When To Use the Mean
When To Use the Mean
• You should use the mean when
–the data are interval or ratio scaled
• Many people will use the mean with ordinally scaled data
too
–and the data are not skewed
• The mean is preferred because it is sensitive to every score
–If you change one score in the data set, the mean will change
9

10. The Median
The Median
10
The median is the midpoint of the
data array.
When the data set is ordered,
whether ascending or descending, it is
called a data array.

11. The Median
The Median
11
Properties of Median
1.The median is unique, there is only one median for
a set of data.
2. The median is found by arranging the set of data
from lowest or highest (or highest to lowest) and
getting the value of the middle observation.

12. The Median
The Median
12
3. Median is not affected by the extreme small
or large values.
4. Median can be applied for ordinal, interval
and ratio data.
5. Median is most appropriate in a skewed
data.

13. How To Calculate the Median
How To Calculate the Median
• Sort the data from highest to lowest
• Find the score in the middle
–middle = (N + 1) / 2
–If N, the number of scores, is even the
median is the average of the middle two
scores
13

14. Median Example
Median Example
• What is the median of the following scores:
10 8 14 15 7 3 3 8 12 10 9
• Sort the scores:
15 14 12 10 10 9 8 8 7 3 3
• Determine the middle score:
middle = (N + 1) / 2 = (11 + 1) / 2 = 6
• Middle score = median = 9 14

15. Median Example
Median Example
• What is the median of the following scores:
24 18 19 42 16 12
• Sort the scores:
42 24 19 18 16 12
• Determine the middle score:
middle = (N + 1) / 2 = (6 + 1) / 2 = 3.5
• Median = average of 3rd
and 4th
scores:
(19 + 18) / 2 = 18.5
15

16. Median Example
Median Example
Find the median of the ages of 9 middle-
management employees of a certain
company. The ages are 53, 45, 59, 48, 54,
46, 51, 58, and 55.
16

17. When To Use the Median
When To Use the Median
• The median is often used when the
distribution of scores is either positively or
negatively skewed
–The few really large scores (positively
skewed) or really small scores (negatively
skewed) will not overly influence the median
17

18. The Mode
•The mode is the
score that occurs
most frequently
in a set of data 0
1
2
3
4
5
6
75 80 85 90 95
Score on Exam 1
Fre
q
u
e
n
c
y
18

19. The Mode
0
1
2
3
4
5
6
75 80 85 90 95
Score on Exam 1
Fre
q
u
e
n
c
y
19
Like the median
and unlike the
mean, extreme
values in a data set
do not affect the
mode.

20. Bimodal
Distributions
•When a
distribution has
two “modes,” it
is called bimodal
0
1
2
3
4
5
6
75 80 85 90 95
Score on Exam 1
Frequency
20

21. Multimodal
Distributions
• If a distribution
has more than 2
“modes,” it is
called multimodal 0
1
2
3
4
5
6
75 80 85 90 95
Score on Exam 1
F
re
q
u
e
n
c
y
21

22. There are some cases when a data set
values have the same number
frequency. When this occurs, the
data set is said to be no mode.
22

23. 23
The following data represent the total
unit sales for Smartphones from a
sample of 10 Communication Centers for
the month of August: 15, 17, 10, 12, 13,
10, 14, 10,8, and 9. Find the mode,
Example of Mode
Example of Mode

24. 24

25. 25

26. When To Use the Mode
When To Use the Mode
• The mode is not a very useful measure of central tendency
–It is insensitive to large changes in the data set
• That is, two data sets that are very different from each other can have
the same mode
26
0
1
2
3
4
5
6
7
1 2 3 4 5 6 7 8 9 10
0
20
40
60
80
100
120
10 20 30 40 50 60 70 80 90 100

27. When To Use the Mode
When To Use the Mode
• The mode is primarily used with nominally
scaled data
–It is the only measure of central tendency
that is appropriate for nominally scaled
data
27

28. Relations Between the
Relations Between the
Measures of Central Tendency
Measures of Central Tendency
• In symmetrical distributions, the
median and mean are equal
– For normal distributions, mean =
median = mode
• In positively skewed distributions,
the mean is greater than the
median
28
In negatively skewed
distributions, the mean is smaller
than the median

29. Weighted Mean
Weighted Mean
 When the mean is computed by giving each data value a weight
that reflects its importance, it is referred to as a weighted mean.
 In the computation of a grade point average (GPA),
In the computation of a grade point average (GPA),
the weights are the number of credit hours earned for
the weights are the number of credit hours earned for
each grade.
each grade.
 When data values vary in importance, the analyst
When data values vary in importance, the analyst
must choose the weight that best reflects the
must choose the weight that best reflects the
importance of each value.
importance of each value.

30. When the mean is computed by
giving each data value a weight
that reflects its importance, it is
referred to as a weighted mean
30
Weighted Mean
Weighted Mean

31. 31

32. In the computation of a grade point
average (GPA), the weights are the
number of credit hours earned for
each grade.
32
Weighted Mean
Weighted Mean

33. When data values vary in
importance, the analyst must
choose the weight that best
reflects the importance of each
value.
33
Weighted Mean
Weighted Mean

34. 34
Weighted Mean Example
Weighted Mean Example