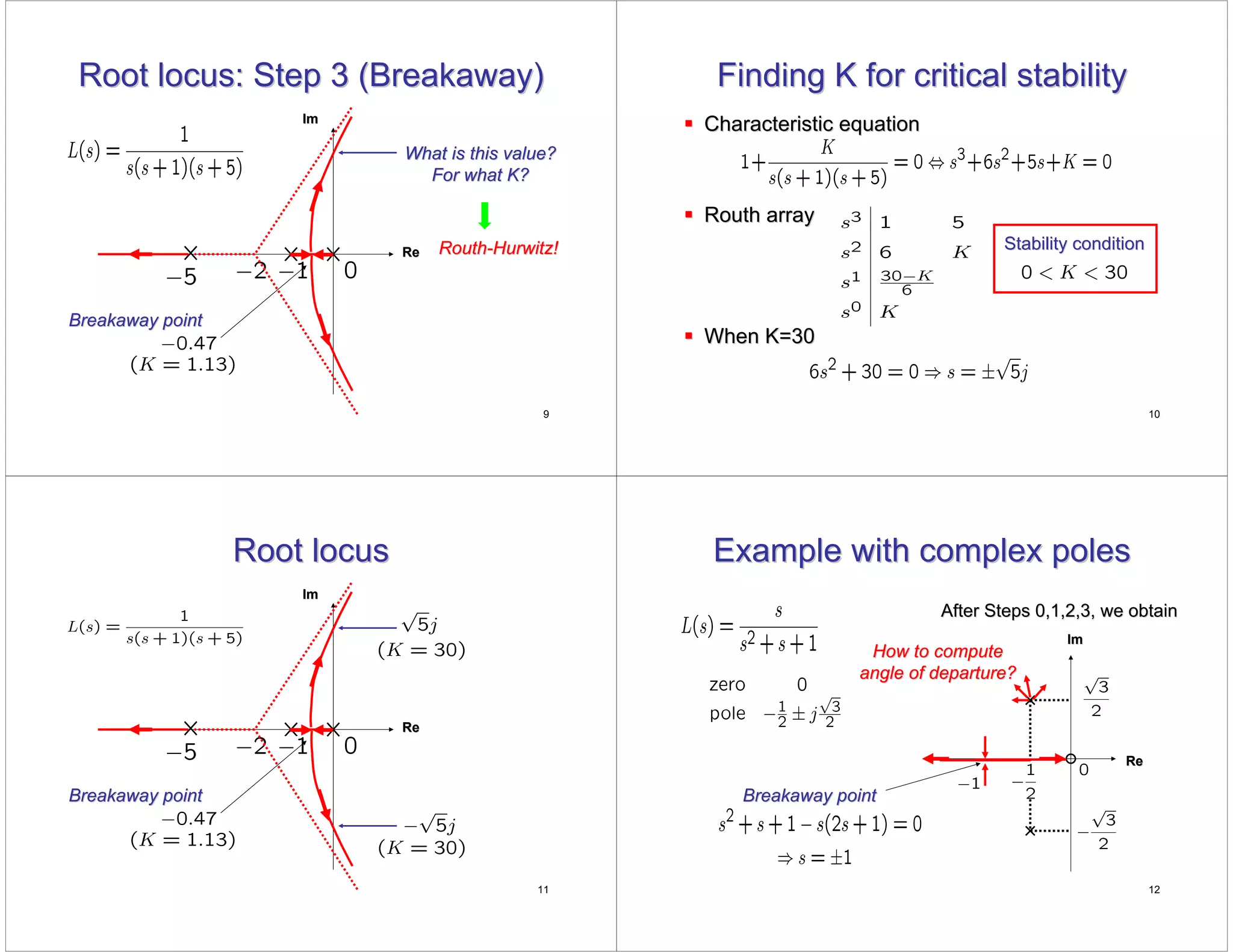
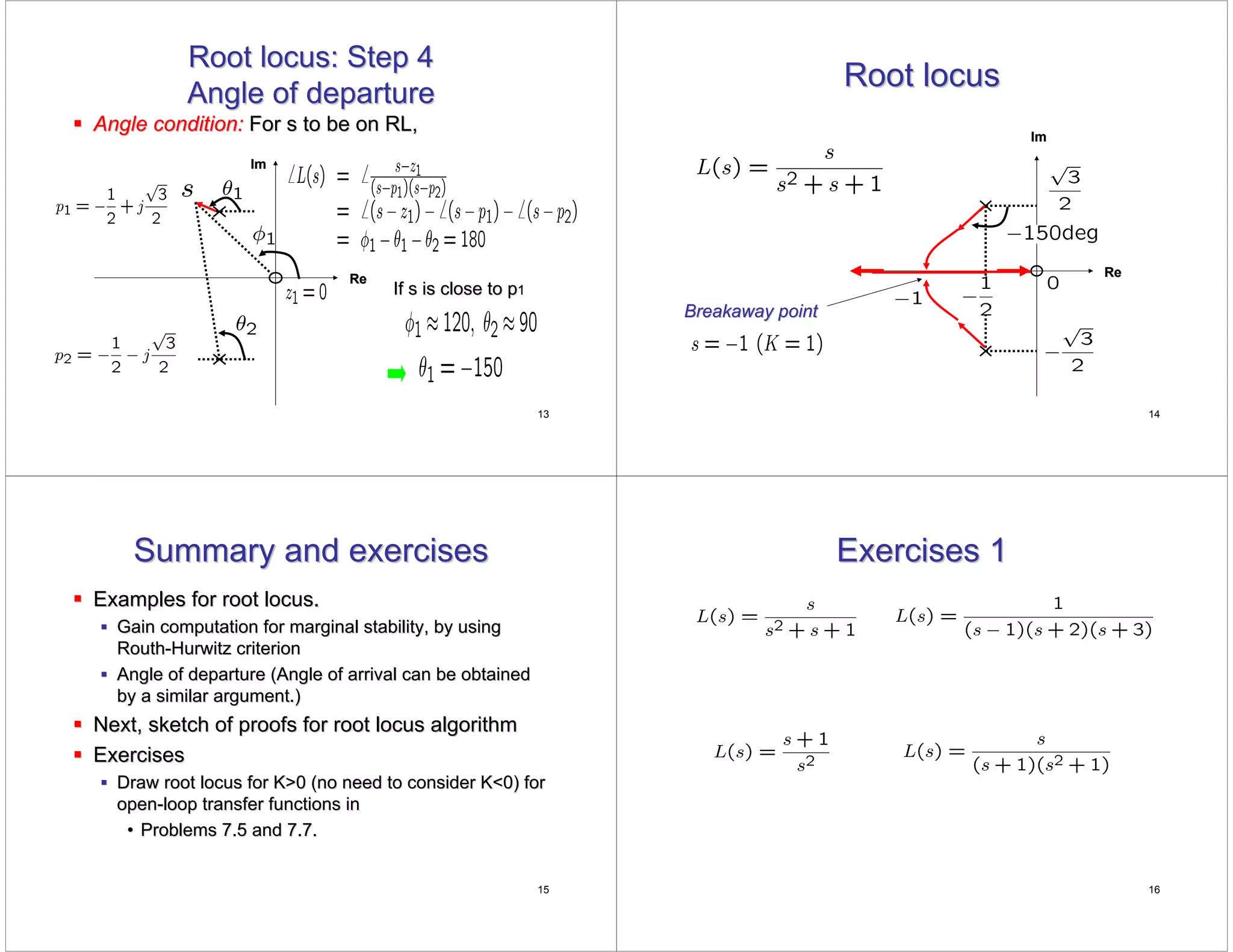
This document discusses root locus analysis, which graphically shows how the poles of a closed-loop system vary with changing gain. It provides examples to demonstrate the steps for sketching root loci, including marking poles and zeros, determining the real axis path and asymptotes, finding breakaway points, and calculating the angle of departure from a complex pole. The document also computes the critical gain for marginal stability using the Routh-Hurwitz criterion and provides exercises for students to practice drawing additional root loci.

1. 1
ME451: Control Systems
ME451: Control Systems
Dr.
Dr. Jongeun
Jongeun Choi
Choi
Department of Mechanical Engineering
Department of Mechanical Engineering
Michigan State University
Michigan State University
Lecture 17
Lecture 17
Root locus: Examples
Root locus: Examples
2
Course roadmap
Course roadmap
Laplace transform
Laplace transform
Transfer function
Transfer function
Models for systems
Models for systems
•
• electrical
electrical
•
• mechanical
mechanical
•
• electromechanical
electromechanical
Block diagrams
Block diagrams
Linearization
Linearization
Modeling
Modeling Analysis
Analysis Design
Design
Time response
Time response
•
• Transient
Transient
•
• Steady state
Steady state
Frequency response
Frequency response
•
• Bode plot
Bode plot
Stability
Stability
•
• Routh
Routh-
-Hurwitz
Hurwitz
•
• Nyquist
Nyquist
Design specs
Design specs
Root locus
Root locus
Frequency domain
Frequency domain
PID & Lead
PID & Lead-
-lag
lag
Design examples
Design examples
(
(Matlab
Matlab simulations &) laboratories
simulations &) laboratories
3
What is Root Locus? (Review)
What is Root Locus? (Review)
ƒ
ƒ Consider a feedback system that has one
Consider a feedback system that has one
parameter (gain) K>0 to be designed.
parameter (gain) K>0 to be designed.
ƒ
ƒ Root locus
Root locus graphically shows how poles of the
graphically shows how poles of the
closed
closed-
-loop system varies as K varies from 0 to
loop system varies as K varies from 0 to
infinity.
infinity.
L(s
L(s)
)
K
K
L(s
L(s): open
): open-
-loop TF
loop TF
4
Root locus: Step 0 (Mark pole/zero)
Root locus: Step 0 (Mark pole/zero)
ƒ
ƒ Root locus is symmetric
Root locus is symmetric w.r.t
w.r.t. the real axis.
. the real axis.
ƒ
ƒ The number of branches = order of
The number of branches = order of L(s
L(s)
)
ƒ
ƒ Mark poles of L with
Mark poles of L with “
“x
x”
” and zeros of L with
and zeros of L with “
“o
o”
”.
.
Re
Re
Im
Im

2. 5
Root locus: Step 1 (Real axis)
Root locus: Step 1 (Real axis)
ƒ
ƒ RL includes all points on real axis to the left of an
RL includes all points on real axis to the left of an
odd number of real poles/zeros.
odd number of real poles/zeros.
ƒ
ƒ RL originates from the poles of L and terminates
RL originates from the poles of L and terminates
at the zeros of L, including infinity zeros.
at the zeros of L, including infinity zeros.
Re
Re
Im
Im
Indicate the direction
Indicate the direction
with an arrowhead.
with an arrowhead.
6
Root locus: Step 2 (Asymptotes)
Root locus: Step 2 (Asymptotes)
ƒ
ƒ Number of asymptotes = relative degree (r) of L:
Number of asymptotes = relative degree (r) of L:
ƒ
ƒ Angles of asymptotes are
Angles of asymptotes are
7
Root locus: Step 2 (Asymptotes)
Root locus: Step 2 (Asymptotes)
ƒ
ƒ Intersections of asymptotes
Intersections of asymptotes
Asymptote
Asymptote
(Not root locus)
(Not root locus)
Re
Re
Im
Im
8
Root locus: Step 3 (Breakaway)
Root locus: Step 3 (Breakaway)
ƒ
ƒ Breakaway points are among roots of
Breakaway points are among roots of
For each candidate s, check the positivity of
For each candidate s, check the positivity of

3. 9
What is this value?
What is this value?
For what K?
For what K?
Re
Re
Im
Im
Root locus: Step 3 (Breakaway)
Root locus: Step 3 (Breakaway)
Breakaway point
Breakaway point
Routh
Routh-
-Hurwitz!
Hurwitz!
10
Finding K for critical stability
Finding K for critical stability
ƒ
ƒ Characteristic equation
Characteristic equation
ƒ
ƒ Routh
Routh array
array
ƒ
ƒ When K=30
When K=30
Stability condition
Stability condition
11
Re
Re
Im
Im
Root locus
Root locus
Breakaway point
Breakaway point
12
Example with complex poles
Example with complex poles
Re
Re
Im
Im
Breakaway point
Breakaway point
After Steps 0,1,2,3, we obtain
After Steps 0,1,2,3, we obtain
How to compute
How to compute
angle of departure?
angle of departure?

4. 13
Root locus: Step 4
Root locus: Step 4
Angle of departure
Angle of departure
ƒ
ƒ Angle condition:
Angle condition: For s to be on RL,
For s to be on RL,
Re
Re
Im
Im
If s is close to p
If s is close to p1
1
14
Root locus
Root locus
Breakaway point
Breakaway point
Re
Re
Im
Im
15
Summary and exercises
Summary and exercises
ƒ
ƒ Examples for root locus.
Examples for root locus.
ƒ
ƒ Gain computation for marginal stability, by using
Gain computation for marginal stability, by using
Routh
Routh-
-Hurwitz criterion
Hurwitz criterion
ƒ
ƒ Angle of departure (Angle of arrival can be obtained
Angle of departure (Angle of arrival can be obtained
by a similar argument.)
by a similar argument.)
ƒ
ƒ Next, sketch of proofs for root locus algorithm
Next, sketch of proofs for root locus algorithm
ƒ
ƒ Exercises
Exercises
ƒ
ƒ Draw root locus for K>0 (no need to consider K<0) for
Draw root locus for K>0 (no need to consider K<0) for
open
open-
-loop transfer functions in
loop transfer functions in
•
• Problems 7.5 and 7.7.
Problems 7.5 and 7.7.
16
Exercises 1
Exercises 1

5. 17
Exercises 2
Exercises 2
18
Exercises 3
Exercises 3
19
Exercises 4
Exercises 4