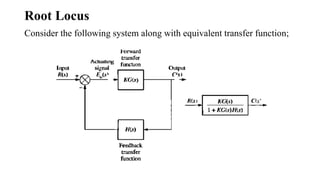
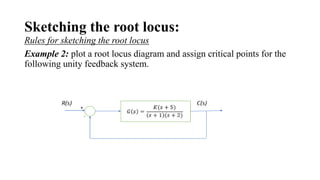
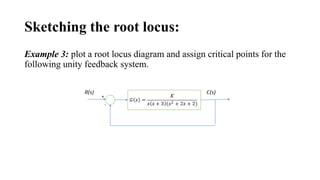
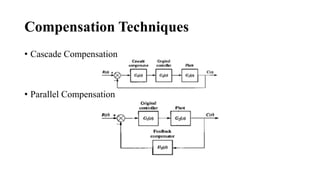
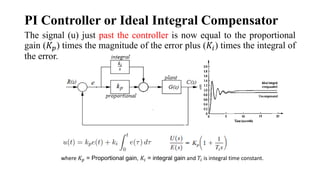
The document discusses the root locus method for analyzing and designing control systems, emphasizing its ability to illustrate system stability and transient response by varying gain. It outlines techniques and rules for sketching root loci, determining closed-loop poles, and identifying critical points, while also introducing compensation methods such as proportional, integral, and derivative control systems. Examples are provided to demonstrate practical applications of these concepts, illustrating how adjustments in system parameters impact performance outcomes.

1. Analysis and Design
Via Root Locus

2. Introduction
• Root locus, a graphical presentation of the closed-loop poles as a
system parameter is varied, is a powerful method of analysis and
design for stability and transient response (Evans. 1948; 1950).
• The root locus can be used to describe qualitatively the performance of
a system as various parameters are changed. For example, the effect of
varying gain upon percent overshoot, settling time, and peak time can
be vividly displayed. The qualitative description can then be verified
with quantitative analysis.
• Besides transient response, the root locus also gives a graphic
representation of a system's stability. We can clearly see ranges of
stability, ranges of instability, and the conditions that cause a system to
break into oscillation.

3. Root Locus
Consider the following system along with equivalent transfer function;
s
s

4. Root Locus
Let,
and
The open loop transfer function is, 𝐾𝐺 𝑠 𝐻 𝑠 , and it’s poles can be
determined since they arise from simple cascaded first and second order
subsystems. But it is difficult to determine the poles of the closed loop
transfer function,𝐺𝑐𝑙 s =
𝐾𝐺 𝑠
1+𝐾𝐺 𝑠 𝐻(𝑠)
, where 𝐾 ≥ 0 𝑖𝑠 𝑔𝑎𝑖𝑛
Which can be written as,
𝐺𝑐𝑙 s =
𝐾𝑁𝐺(𝑠)𝐷𝐻(𝑠)
𝐷𝐺 𝑠 𝐷𝐻 𝑠 + 𝐾𝑁𝐺 𝑠 𝑁𝐻 𝑠
The root locus will be used to give us a vivid picture of the poles of
𝐺𝑐𝑙 s as K varies.
where N and D are factored polynomials and
signify numerator and denominator terms,
respectively.

5. Root Locus
The root locus technique can be used to analyze and design the effect of
gain upon the system's transient response and stability. As the gain
varies, the closed loop poles move on a complex plane i.e. it can be real
and distinct, real and repeated, complex or purely imaginary. It is this
representation of the paths of the closed-loop poles as the gain is
varied that we call a root locus.
Example 1: plot a root locus diagram for the following unity feedback
system.

6. Root Locus
Properties of the root locus help us to make a rapid sketch of the root locus for
higher-order systems without having to factor the denominator of the closed-
loop transfer function.
A pole, s of the closed loop transfer function 𝐺𝑐𝑙 s =
𝐾𝐺 𝑠
1+𝐾𝐺 𝑠 𝐻(𝑠)
exists when the characteristic polynomial in the denominator becomes zero, or
when 𝐾𝐺 𝑠 𝐻 𝑠 become -1.
Alternatively, s, is a closed loop pole if,
𝐾𝐺 𝑠 𝐻 𝑠 = 1, 𝑜𝑟 𝑘 =
1
𝐺 𝑠 𝐻 𝑠
𝑴𝒂𝒈𝒏𝒊𝒕𝒖𝒅𝒆 𝒄𝒓𝒊𝒕𝒆𝒓𝒊𝒂 𝑎𝑛𝑑
𝑎𝑛𝑔𝑙𝑒 𝑜𝑓 𝐾𝐺 𝑠 𝐻 𝑠 = 2k + 1 1800, 𝑘 = 0, ±1, ±2, ±3 (𝑨𝒏𝒈𝒍𝒆 𝒄𝒓𝒊𝒕𝒆𝒓𝒊𝒂)
The values of s that fulfill both the angle and magnitude conditions are the roots
of the characteristic equation, or the closed-loop poles.

7. Root Locus
We have just found that a pole of the closed-loop system causes the angle of
KG(s)H(s), or simply G(s)H(s) since K is a scalar, to be an odd multiple of
1800 . In other words, given the poles and zeros of the open-loop transfer
function, KG(s)H(s) , a point in the s-plane is on the root locus for a particular
value of gain, K, if the angles of the zeros minus the angles of the poles, all
drawn to the selected point on the s-plane, add up to (2k + 1) 1800 where,
𝑘 = 0, ±1, ±2, ±3 …
Furthermore, the magnitude of KG(s)H(s) must be unity, implying that the
value of K is the reciprocal of the magnitude of G(s)H(s) when the pole value
is substituted for s.
Where magnitude of G(s)H(s) is;
𝑮 𝒔 𝑯 𝒔 =
𝒛𝒆𝒓𝒐 𝒍𝒆𝒏𝒈𝒕𝒉𝒔
𝒑𝒐𝒍𝒆 𝒍𝒆𝒏𝒈𝒕𝒉𝒔

8. Root Locus
Sketching the root locus:
It appears from our previous discussion that the root locus can
be obtained by sweeping through every point in the s-plane to
locate those points which the angles, as previously described,
add up to an odd multiple of 1800 . Although this task is tedious
without the aid of a computer, the concept can be used to
develop rules that can be used to sketch the root locus without
the effort required to plot the locus.
Once a sketch is obtained, it is possible to accurately plot just
those points that are of interest to us for a particular problem.
The rules yield a sketch that gives intuitive insight into the
behavior of a control system.

9. Sketching the root locus:
Rules for sketching the root locus
Rule-1: The number of branches of the root locus equals the number of
closed-loop poles.
Rule-2: The root locus is symmetrical about the real axis.
Rule-3: On the real axis, for K > 0 the root locus exists to the left of an
odd number of real-axis, finite open-loop poles and/or finite open-loop
zeros.
Rule-4: The root locus begins at the finite and infinite poles of open
loop transfer function, G(s)H(s) and ends at the finite and infinite zeros
of open loop transfer function, G(s)H(s).

10. Sketching the root locus:
Rules for sketching the root locus
Rule-5: The point where the locus leaves the real axis, is called the breakaway
point, and the point where the locus returns to the real axis, is called the break-in
point. The root locus breaks away from the real axis at a point where the gain is
maximum between open loop poles, and breaks into the real axis at a point where
the gain is minimum between two zeros.
This point is found by rearranging the closed loop transfer function characteristics
equation for gain, K and solve for the point by differentiating it with respect to s and
equating it to zero.
Also, break away and break in points satisfy the relationship;
𝟏
𝒔 + 𝒛𝒊
=
𝟏
𝒔 + 𝒑𝒊
Where 𝑧𝑖 and 𝑝𝑖are negative of open loop zeros and poles respectively
At the breakaway or break-in point, the branches of the root locus form an angle of
1800
𝑛 with the real axis, where n is the number of closed-loop poles arriving at or
departing from the single breakaway or break-in point on the real axis.

11. Sketching the root locus:
Rules for sketching the root locus
Rule-5: Cont…
If a root locus lies between two adjacent open-loop poles on the real
axis, then there exists at least one breakaway point between the two
poles. Similarly, if the root locus lies between two adjacent zeros (one
zero may be located at infinity) on the real axis, then there always exists
at least one break-in point between the two zeros. If the root locus lies
between an open-loop pole and a zero (finite or infinite) on the real axis,
then there may exist no breakaway or break-in points or there may exist
both breakaway and break-in points.

12. Sketching the root locus:
Rules for sketching the root locus
Example 2: plot a root locus diagram and assign critical points for the
following unity feedback system.

13. Sketching the root locus:
Rules for sketching the root locus
Rule-6: The root locus approaches straight lines as asymptotes as the
locus approaches infinity. Furthermore; the equation of the asymptotes
is given by the real-axis intercept, and angle in as follows.
𝝈𝒂 =
𝒇𝒊𝒏𝒊𝒕𝒆 𝒓𝒆𝒂𝒍 𝒑𝒐𝒍𝒆𝒔− 𝒇𝒊𝒏𝒊𝒕𝒆 𝒓𝒆𝒂𝒍 𝒛𝒆𝒓𝒐𝒔
#𝒇𝒊𝒏𝒊𝒕𝒆 𝒑𝒐𝒍𝒆𝒔−#𝒇𝒊𝒏𝒊𝒕𝒆 𝒛𝒆𝒓𝒐𝒔
𝜽𝒂 =
(𝟐𝒌+𝟏)×𝟏𝟖𝟎
#𝒇𝒊𝒏𝒊𝒕𝒆 𝒑𝒐𝒍𝒆𝒔−#𝒇𝒊𝒏𝒊𝒕𝒆 𝒛𝒆𝒓𝒐𝒔
where,𝑘 = 0, ±1, ±2, ±3 …
Here, k=0 corresponds to the asymptotes with the smallest angle with
the real axis. Although k assumes an infinite number of values, as k is
increased the angle repeats itself, and the number of distinct asymptotes
is #𝑓𝑖𝑛𝑖𝑡𝑒 𝑝𝑜𝑙𝑒𝑠 − #𝑓𝑖𝑛𝑖𝑡𝑒 𝑧𝑒𝑟𝑜𝑠 − 1.

14. Sketching the root locus:
Rules for sketching the root locus
Rule-7: The 𝑗𝜔-axis crossing is a point on the root locus that separates the
stable operation of the system from the unstable operation. The root locus
crosses the 𝑗𝜔-axis at the point;
where 𝑎𝑛𝑔𝑙𝑒 𝑜𝑓𝐺 𝑠 𝐻 𝑠 = 2k + 1 1800
(𝑎𝑛𝑔𝑙𝑒 𝑐𝑟𝑖𝑡𝑒𝑟𝑖𝑎).
Routh-Hurwitz can be used to find the 𝑗𝜔-axis crossing.
The values of 𝜔 thus found give the frequencies at which root loci cross the
imaginary axis. The 𝐾 value corresponding to each crossing frequency gives the
gain at the crossing point.

15. Sketching the root locus:
Rules for sketching the root locus
Rule-8: The root locus departs from complex, open loop poles and
arrives at complex, open-loop zeros at angles that can be calculated as
follows.
Angle of departure: 𝜑𝑑 = ±180𝑜 2𝑘 + 1 + 𝑧𝑒𝑟𝑜 𝑎𝑛𝑔𝑙𝑒 − 𝑝𝑜𝑙𝑒 𝑎𝑛𝑔𝑙𝑒𝑠
Angle of arrival: 𝜑𝑎 = ±180𝑜 2𝑘 + 1 − 𝑧𝑒𝑟𝑜 𝑎𝑛𝑔𝑙𝑒 + 𝑝𝑜𝑙𝑒 𝑎𝑛𝑔𝑙𝑒𝑠

16. Sketching the root locus:
Example 3: plot a root locus diagram and assign critical points for the
following unity feedback system.

17. Control System Design Using Root Locus
Setting the gain at a particular value yields the transient response dictated
by the poles at that point on the root locus. But we are limited to those
responses that exist along the root locus.
We augment or compensate, the system with additional poles and zeros
in the forward path , so that the compensated system has a root locus that
goes through the desired pole location for some value of gain
Addition of compensating poles and zeros need not interfere with the
power output requirements of the system or present additional load or
design problems. Compensating poles and zeros can be generated with a
passive or an active network.

18. Control System Compensation Using Root Locus
Transient response is improved with the addition of differentiation, and
steady-state error is improved with the addition of integration in the
forward path.
Systems that feed the error forward to the plant are called proportional
control systems. Systems that feed the integral of the error to the plant are
called integral control systems. Finally, systems that feed the derivative of
the error to the plant are called derivative control systems.
Proportional Controller

19. Compensation Techniques
• Cascade Compensation
• Parallel Compensation

20. Ideal integral compensator and Lag Compensator
Steady state error can be improved by placing an open-loop pole at the
origin, because this increases the system type by one.
The first technique is ideal integral compensation (implemented with active
networks, such as amplifiers), which uses a pure integrator to place an open-
loop, forward-path pole at the origin, thus increasing the system type and
reducing the error to zero. We also add a zero close to the pole to keep the
root locus go through the desired point and keep the gain the same as before.
The second technique does not use pure integration. This compensation
technique places the pole near the origin (can be implemented with a less
expensive passive network that does not require additional power sources),
and although it does not drive the steady-state error to zero, it does yield a
measurable reduction in steady-state error.
Implemented by PI controller

21. PI Controller or Ideal Integral Compensator
The signal (u) just past the controller is now equal to the proportional
gain (𝐾𝑝) times the magnitude of the error plus (𝐾𝑖) times the integral of
the error.
where 𝐾𝑝 = Proportional gain, 𝐾𝑖 = integral gain and 𝑇𝑖 is integral time constant.

22. Ideal derivative compensator and Lead Compensator
The result of adding differentiation is the addition of a zero to the
forward-path transfer function which improves the transient response.
• The first technique is an ideal derivative compensator, in which a pure
differentiator is added to the forward path of the feedback control
system (require active network for its realization).
The ideal derivative compensator is implemented with PD controller.
Differentiation of high frequencies can lead to large unwanted signals of
saturation of amplifiers and other components.
• The second technique approximate differentiation with passive
network by adding zero and more distant pole to the forward path
transfer function.

23. PD Controller or Ideal derivative compensator
Judicious choice of the position of the compensator zero can
quicken the response over the uncompensated system.
where 𝐾𝑝 = Proportional gain, 𝐾𝑑 = Derivative gain and 𝑇𝑑 is derivative time constant.

24. Ideal integral-derivative compensator and
Lag-lead compensator
Ideal integral-derivative compensator
- Implemented by PID controller
Lead-lag compensator

25. PID controller and Lead-lag compensator
The error signal e(t) will be sent to the PID controller, and the
controller computes both the derivative and the integral of this
error signal. The signal (u) just past the controller is now equal to
the proportional gain (Kp) times the magnitude of the error plus
the integral gain (Ki) times the integral of the error plus the
derivative gain (Kd) times the derivative of the error. The
proportional part acts on the present value of the error, the integral
represents an average of past errors and the derivative can be
interpreted as a prediction of future errors based on linear
extrapolation
𝐾𝑝 +
𝐾𝑖
𝑠
+ 𝐾𝑑𝑠 =
𝐾𝑑𝑠2
+𝐾𝑝 𝑠 + 𝐾𝑖
𝑠

26. Compensator design procedure

27. PID controller and Lead-lag compensator
Example-1, [Norman Nise]
Given the system of figure below,
design a PD controller so that the
system can operate with a peak time
that is two thirds of that of
uncompensated system (0.3 sec) at
20% overshoot. The root locus of
uncompensated system is shown to
the right.

28. PID controller and Lead-lag compensator
Example-2 [Norman Nise]
Upgrade the controller in example-1 to a PID controller that reduce the
steady state error to zero for a step input.