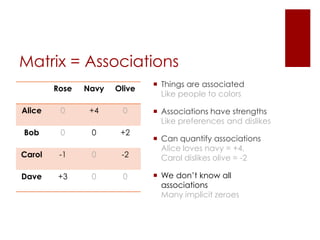
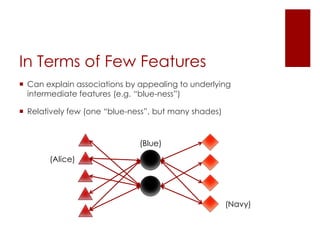
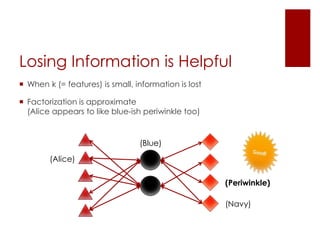
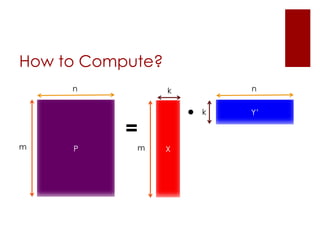
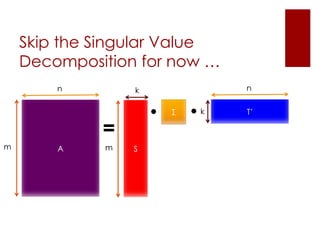
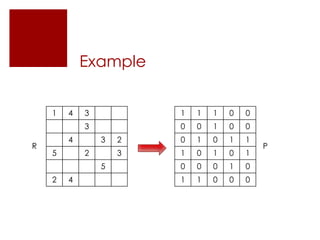
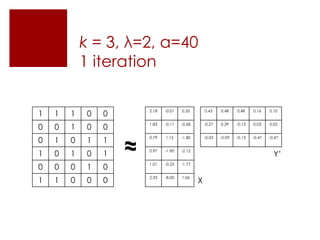
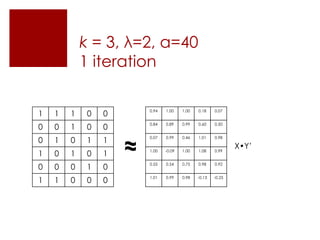
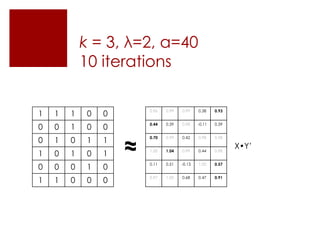
This document discusses matrix factorization techniques for recommendation systems. It explains that user-item interaction data can be represented as a matrix and decomposed into two lower-rank matrices that capture latent features. One matrix represents users and the other represents items. The document outlines an alternating least squares algorithm to compute the decomposed matrices and discusses how the technique can be implemented in Apache Mahout and Myrrix for scalable recommendations.

1. 6 42 8
78 14 98
1 7 8
Simple Matrix Factorization for
Recommendation
Sean Owen • Apache Mahout

2. Apache Mahout
• Scalable machine learning
• (Mostly) Hadoop-based
• Clustering, classification and
recommender engines
• Nearest-neighbor
• User-based mahout.apache.org
• Item-based
• Slope-one
• Clustering-based
• Latent factor
• SVD-based
• ALS
• More!

3. Matrix = Associations
 Things are associated
Rose Navy Olive
Like people to colors
Alice 0 +4 0  Associations have strengths
Like preferences and dislikes
Bob 0 0 +2
 Can quantify associations
Alice loves navy = +4,
Carol -1 0 -2 Carol dislikes olive = -2
Dave +3 0 0  We don’t know all
associations
Many implicit zeroes

4. From One Matrix, Two
 Like numbers, matrices can n
be factored
 m•n matrix = m•k times k•n
 Associations can
m P
=
decompose into others
k n
 Alice likes navy =
•
Alice loves blues, and
k Y’
blues includes navy m X

5. In Terms of Few Features
 Can explain associations by appealing to underlying
intermediate features (e.g. “blue-ness”)
 Relatively few (one “blue-ness”, but many shades)
(Blue)
(Alice)
(Navy)

6. Losing Information is Helpful
 When k (= features) is small, information is lost
 Factorization is approximate
(Alice appears to like blue-ish periwinkle too)
(Blue)
(Alice)
(Periwinkle)
(Navy)

7. How to Compute?
n k n
• k Y’
=
m P m X

8. Skip the Singular Value
Decomposition for now …
n k n
• Σ •k T’
=
m A m S

9. Alternating Least Squares
 Collaborative Filtering for Implicit Feedback Datasets
www2.research.att.com/~yifanhu/PUB/cf.pdf
 R = matrix of user-item interactions “strengths”
 P = R reduced to 0 and 1
 Factor as approximate P ≈ X•Y’
 Start with random Y
 Compute X such that X•Y’ best approximates P
(Frobenius / L2 norm) (Least Squares)
 Repeat for Y (Alternating)
 Iterate, Iterate, Iterate
 Large values in X•Y’ are good recommendations

10. Example
1 4 3 1 1 1 0 0
3 0 0 1 0 0
4 3 2 0 1 0 1 1
R P
5 2 3 1 0 1 0 1
5 0 0 0 1 0
2 4 1 1 0 0 0

11. k = 3, λ=2, α=40
1 iteration
1 1 1 0 0 2.18 -0.01 0.35 0.43 0.48 0.48 0.16 0.10
0 0 1 0 0 1.83 -0.11 -0.68 -0.27 0.39 -0.13 0.03 0.05
≈
0 1 0 1 1 0.79 1.15 -1.80 -0.03 -0.09 -0.13 -0.47 -0.47
1 0 1 0 1 0.97 -1.90 -2.12
Y’
0 0 0 1 0 1.01 -0.25 -1.77
1 1 0 0 0 2.33 -8.00 1.06
X

12. k = 3, λ=2, α=40
1 iteration
1 1 1 0 0
0.94 1.00 1.00 0.18 0.07
0 0 1 0 0 0.84 0.89 0.99 0.60 0.50
≈
0 1 0 1 1 0.07 0.99 0.46 1.01 0.98
X•Y’
1 0 1 0 1 1.00 -0.09 1.00 1.08 0.99
0 0 0 1 0 0.55 0.54 0.75 0.98 0.92
1 1 0 0 0 1.01 0.99 0.98 -0.13 -0.25

13. k = 3, λ=2, α=40
10 iterations
1 1 1 0 0
0.96 0.99 0.99 0.38 0.93
0 0 1 0 0 0.44 0.39 0.98 -0.11 0.39
≈
0 1 0 1 1 0.70 0.99 0.42 0.98 0.98
X•Y’
1 0 1 0 1 1.00 1.04 0.99 0.44 0.98
0 0 0 1 0 0.11 0.51 -0.13 1.00 0.57
1 1 0 0 0 0.97 1.00 0.68 0.47 0.91

14. Interesting Because…
This is all very
parallelizable
by row, column

15. BONUS: Folding in New Data
 Model building takes time  Apply some right inverse:
⌃
X•Y’•(Y’)-1 = Q•(Y’)-1 = so
 Sometimes need X = Q•(Y’)-1
immediate, if approximate,
updates for new data  OK, what is (Y’)-1?
 For new user U, need new  Of course (Y’•Y)•(Y’•Y)-1 = I
row, XU•Y’ = QU, but have PU
 So Y’•(Y•(Y’•Y)-1) = I and
 What is XU? right inverse is Y•(Y’•Y)-1
 Xu = QU•Y•(Y’•Y)-1 and so
Xu ≈ Pu•Y•(Y’•Y)-1

16. In Mahout
 org.apache.mahout.cf.  MAHOUT-737
taste.hadoop.als.
ParallelALSFactorizationJob  Alternate implementation
 Alternating least squares of alternating least
squares
 Distributed, Hadoop-
based  And more…
 org.apache.mahout.cf.  DistributedLanczosSolver
taste.impl.recommender.  SequentialOutOfCoreSvd
svd.SVDRecommender
 …
 SVD-based
 Non-distributed, not
Hadoop

17.  Complete product
 Real-time Serving Layer
Myrrix  Hadoop-based
Computation Layer
 Tuned, documented
 Free / open: Serving Layer,
for small data
 Commercial: add
Computation Layer for big
data; Hosting
 Matrix factorization-based,
attractive properties
 http://myrrix.com

18. Thank You
srowen at myrrix.com
mahout.apache.org