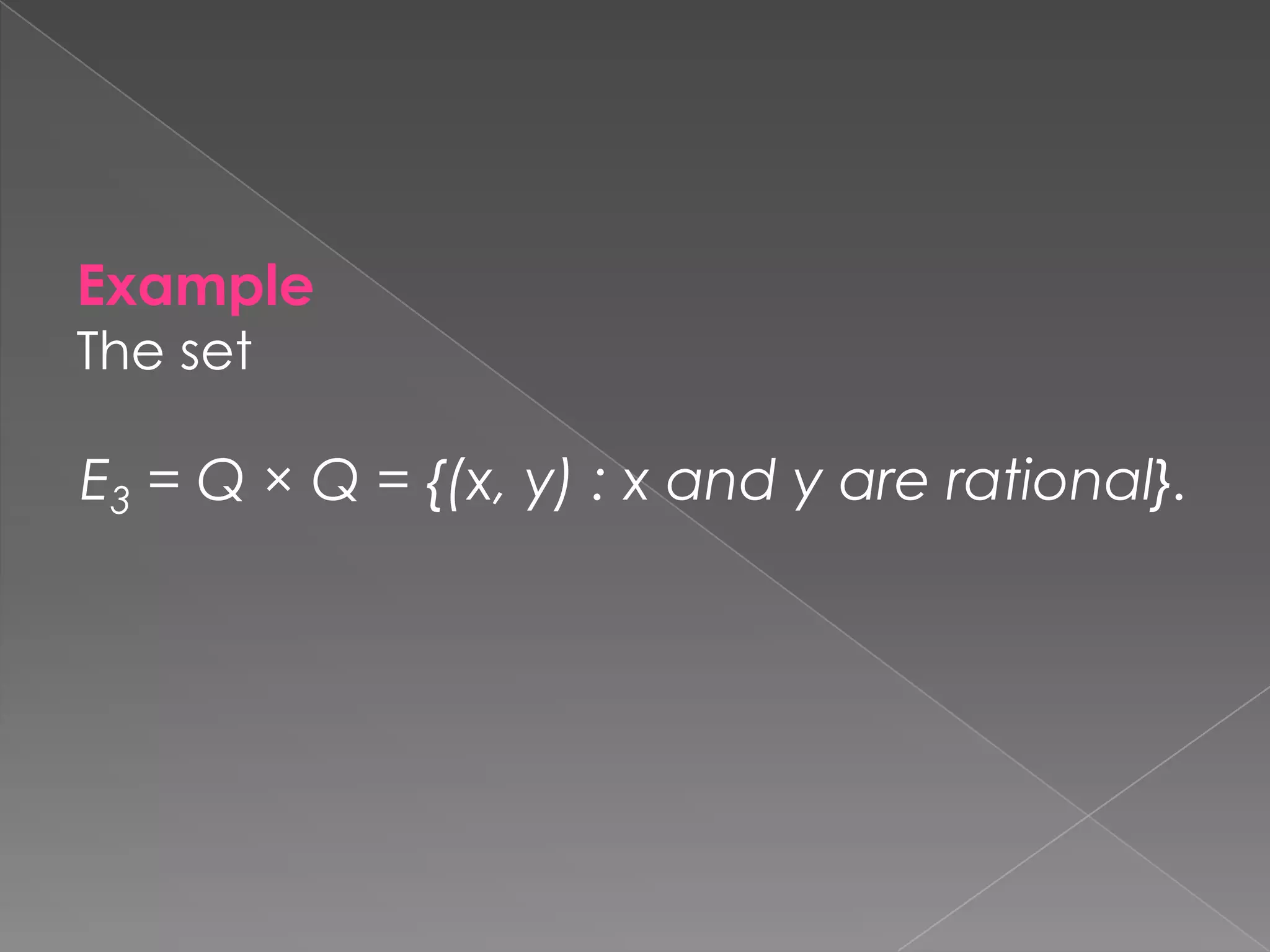The document defines key concepts related to sequences and limits in multivariable calculus including open balls, open and closed sets, accumulation points, bounded sequences, and convergence of sequences in Rn. It proves that a set is closed if and only if it contains all its limit points. It also proves that every bounded sequence in Rn contains a convergent subsequence using the Bolzano-Weierstrass theorem and taking subsequences of the coordinates.

1. Aujero, Gadian, Pamonag

2. Let x0 ∈ R, and let r > 0. The set
B(x0, r) = {x : ||x − x0 || < r}
is called the open ball of radius r centered
at x0. It is also called the r-neighborhood
of x0 which consists the points in Rn whose
distance from x0 is less than r.

3. We define a number of terms, familiar in
our study of R, in terms of this simple
concept.
1. A set E in Rn is open if to each x0 ∈ E there
corresponds an ε > 0 such that B(x0, ε) ⊂
E. An open set containing a point x0 is
also called a neighborhood of x0.

4. 2. A set E in Rn is closed if Rn E is open.
3. A point x0 ∈ E ⊂ Rn is an accumulation
point, or limit point, of E if every open ball
centered at x0 contains points of E other
than X0. We shall use the terms
“accumulation point” and “limit point”
interchangeably.

5. 4. A point x0 ∈ Rn is a boundary point of a
set E ⊂ Rn provided that for each ε > 0,
B(x0, ε) ∩ E ≠ ∅ and B(x0, ε) E ≠ ∅.
5. A set E ⊂ Rn is bounded if there exists
M>0 such that E ⊂ B(0,M).

6. Example
The set
E3 = Q × Q = {(x, y) : x and y are rational}.

7. • The set is neither open nor closed.
• Every point in R2 is an accumulation point
of E3 and a boundary point of E3.
• E3 is not bounded in R2.

9. A sequence of points in Rn is a function
f : IN → Rn.
As was the case for sequences in R, we will
frequently use notation such as {xk} to
denote a sequence in Rn. Here each vector
xk can be written as an n-tuple using double
subscript notation:
xk = (xk1 xk2, . . . , xkn).

10. A sequence {xk} in Rn is bounded if there exists
M ∈ IN such that ||xk|| ≤ M for all k ∈ IN.
We can define convergence of a sequence
{xk} in Rn in the same way as we did for
sequences of real numbers (Definition 2.6).
Note that here the norm plays the same
role that the absolute value did earlier.

11. Let {xk} be a sequence in Rn. We say {xk}
converges to a point x and write
lim xk = x
k→∞
or
xk → x as k→∞
provided that for each ε > 0 there exists N ∈ IN
such that || xk – x || < ε whenever k ≥ N.

12. This definition is equivalent to the requirement
that every open ball centered at x contains
all but a finite number of terms of the
sequence: For each ε > 0 there exists N such
that xk ∈ B(x, ε) for all k ≥ N. It is also
equivalent to the requirements
|| xk − x || → 0
or
d(xk, x) → 0
as k→∞, where d is the euclidean distance.

13. We can also describe convergence in Rn in
terms of coordinate-wise convergence. T o
see this, observe first that for
x = (x1, x2, . . . , xn) and j = 1, . . . , n,
n
n
Thus
x j 2 ≤ Σ xi2 = ||x||2 ≤ ( Σ|xi|)2.
i=1
i=1
n
|xj| ≤ ||x|| ≤ Σ |xi|.
i=1
(7)

14. Now let
{xk} = {(xk1 , xk2 , . . . , xkn)}
be a sequence in Rn, and let
x = (x1, x2 , . . . , xn) be a point in Rn. By (7)
|xkj − xj| ≤ ||xk − x|| ≤
n
Σ |xki − xi|.
i=1
(8)

15. If xk → x as k→∞, that is,
||xk − x|| → 0 as k → ∞,
then we see from (8) that for each j = 1, . . . ,
n, |xkj − xj| → 0 as k → ∞. Conversely, if for
each j = 1, . . . , n we have |xkj − xj| → 0 as
k → 0, then
n
Σ |xki − xi| → 0
i=1
as k→∞, so we see once again from (8) that
||xk − x|| → 0 as k→∞. We summarize this
discussion as a theorem.

16. Let
{xk} = {(xk1, . . . , xkn)}
be
a
sequence
in
Rn
x = (x1, x2, . . . , xn) ∈ Rn. Then
lim xk = x
k→∞
and
let
if and only if for each j = 1, . . . , n, limk→∞ xkj = xj .

17. Let {xk} and {yk} be sequences in Rn, and let α ∈
R. If limk→∞ xk = x and limk→∞ yk = y, then
i. lim k→∞ (αxk) = αx.
ii. lim k→∞ (xk + yk) = x + y.
iii. lim k→∞ (xk ・ yk) = x ・ y.

18. Limit Points As was true in R, we can
characterize limit points in Rn in the language
of sequences.
Let E ⊂ Rn and let x ∈ Rn. Then x is a limit point of
E if and only if there exists a sequence {xk} of
distinct points of E such that limk→∞ xk = x.

19. Suppose x is a limit point of E.
Then for each ε > 0 there exists xk ≠ x in E such
that ||xk − x|| < ε.
Choose x1 ∈ E such that 0 < ||x1 − x || < 1.
Inductively, having chosen xk, choose xk+1 in E
such that
0 < || xk+1 − x || < ½ || xk − x ||.
Then limk→∞xk = x, xk ≠ x, and if k ≠ j, xk ≠ xj. The
converse is obvious.

20. A set E ⊂ Rn is closed if and only if it contains all
its limit points.

21. (⇒): Let E be a closed set, and let {xn} be a
sequence in E that converges to x0 ∈ X.
We must show that x0 ∈ E.
Suppose that x0 ∈ E is not true, we assume that
x ∈ E c.
Since Ec is open, there is an ε > 0 for which
B(x0, ε) is a subset of Ec. Since {xn} → x0, let ň
be such that n > ň ⇒ d(xn, x0) < ε, ε > 0. Then
for n > ň we have both xn ∈ E and xn ∈ B(x0,
ε) ) is a subset of Ec, a contradiction.

22. (⇐): Suppose E is not closed.
We must show that E does not contain all its
limit points.
Since E is not closed, Ec is not open.
Therefore there is at least one element x of Ec
such that every ball B(x0, ε) contains at least
one element of (Ec)c = E. For every n ∈ IN, let
xn ∈ B(x, 1/n) ∩ E. Then we have a sequence
{xn} in E which converges to x ɆE | i.e., x is a
limit point of E but is not in E, so E does not
contain all its limit points.

23. Every bounded sequence {xk} in Rn contains a
convergent subsequence.

24. Let {xk} be a bounded sequence in Rn,
say ||xk || ≤ M for all k ∈ IN.
For each k, let xk = (xk1, . . . , xkn). Then for each
k ∈ IN and j = 1, . . . , n, |xkj| ≤ M. Thus, for all
j, the sequence of real numbers {xkj} is
bounded.

25. Let j = 1.By the Bolzano-Weierstrass theorem
applied to the bounded sequence
{xkj} (k = 1, 2, 3, . . . ) there exists a sequence
of integers
1 ≤ k(1, 1) < k(1, 2) < . . .
and a number x1 such that
xk(1,i),1→ x1 as i→∞.
Observe that the sequence {xk(1,i),1} is just a
subsequence of the sequence {xk1}.

26. Next let j = 2.
The sequence {xk(1,i),2} is also bounded by M, so
again, by the Bolzano-Weierstrass theorem
there is a subsequence {k(2, i)} of {k(1, i)}
such that xk(2,i),2 converges.
L et
x2 = lim i→∞ xk(2,i),2.
Now, the sequence {xk(1,i),1} converges to x1, so
the same is true of any subsequence of this
sequence. In particular {xk(2,i),1} → x1 as i→∞.

27. We continue this process. Having obtained a
sequence
{xk(j,i),j} with {xk(m,i),m} → xm for all m ≤ j,
we use the Bolzano-Weierstrass theorem yet
again to obtain a further subsequence
{xk(j+1,i),j+1} that converges to a point xj+1 ∈ R.
The process stops when j + 1 = n. Letting ki =
k(n, i) and x = (x1, . . . , xn), we have
limi→∞ xki = x by Theorem 11.15.