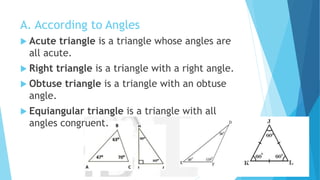
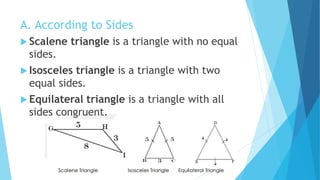
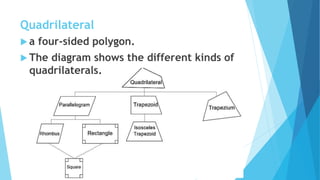
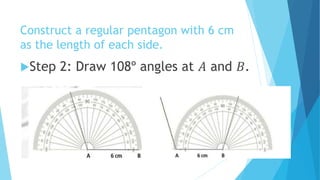
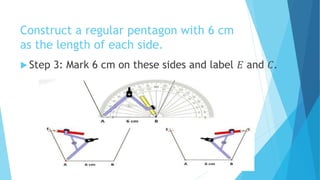
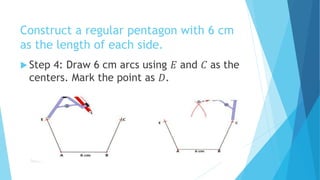
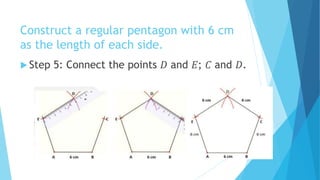
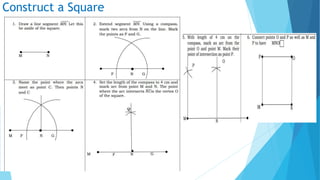
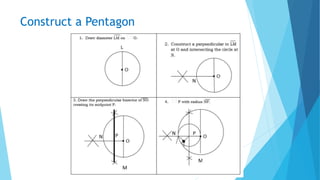
This document provides information about constructing different types of polygons and solving problems involving polygons. It defines triangles, quadrilaterals, and regular polygons. It discusses classifying triangles by angles and sides. It describes different types of quadrilaterals including parallelograms, rectangles, squares, trapezoids, isosceles trapezoids, and trapeziums. The document provides step-by-step examples for constructing triangles, squares, rectangles, pentagons, and hexagons. It includes examples of constructing polygons given specific side lengths or included angles. Finally, it provides practice problems for constructing various polygons.

1. Constructing Polygons
and Solving Problems
Involving Polygons

2. Triangle
 a polygon having three sides.
 can be classified according to angles and
sides.

3. A. According to Angles
 Acute triangle is a triangle whose angles are
all acute.
 Right triangle is a triangle with a right angle.
 Obtuse triangle is a triangle with an obtuse
angle.
 Equiangular triangle is a triangle with all
angles congruent.

4. A. According to Sides
 Scalene triangle is a triangle with no equal
sides.
 Isosceles triangle is a triangle with two
equal sides.
 Equilateral triangle is a triangle with all
sides congruent.

5. Quadrilateral
 a four-sided polygon.
 The diagram shows the different kinds of
quadrilaterals.

6. A parallelogram is a quadrilateral
with two pairs of opposite sides
that are parallel.
A rhombus (plural: rhombi) is a
parallelogram with four congruent
sides.
A rectangle is a parallelogram
with four congruent angles. Each
interior angle measures 90O.

7. A square is a parallelogram with four
congruent sides and four congruent
angles.
A trapezoid is a quadrilateral with only
one pair of opposite sides that are
parallel.
An isosceles trapezoid is a trapezoid
whose non-parallel sides are congruent.
A trapezium is a quadrilateral with no
pair of opposite sides that are parallel.

8. Constructing Polygons

9. Example 1 Construct △ 𝐴𝐵𝐶 such that 𝐴
𝐵̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = 3 𝑐𝑚, 𝐵𝐶̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = 5 𝑐𝑚 and 𝐴𝐶̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = 4 𝑐𝑚
Step 1: Draw 𝐵𝐶̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ of 5 cm
using a ruler.
Step 2: With 𝐵 as the center and radius of
3 cm (𝐴𝐵̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = 3 𝑐𝑚), draw an arc using a
compass.

10. Example 1 Construct △ 𝐴𝐵𝐶 such that 𝐴
𝐵̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = 3 𝑐𝑚, 𝐵𝐶̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = 5 𝑐𝑚 and 𝐴𝐶̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = 4 𝑐𝑚
Step 3: With 𝐶 as the center and
radius of 4 cm (𝐴𝐵̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = 4 𝑐𝑚),
draw an arc to cut the previous
at 𝐴.
Step 4: Draw a segment 𝐴𝐵̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ and 𝐴𝐶̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅
using a ruler to get △ 𝐴𝐵𝐶

11. Example 2: Construct a square having 4
cm as length of each side.
Step 1: Draw 𝐴𝐵̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ of length
4 cm. Extend 𝐴𝐵̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ to the
right.
Step 2: Draw an arc on each side 𝐵 using
any compass width. Label these 𝑀 and 𝑁.

12. Step 3: With the compass on 𝑁
and any width, draw an arc
above 𝐵.
Step 4: Without changing the width,
draw an arc using point 𝑀 and name
it 𝑂.
Example 2: Construct a square having 4
cm as length of each side.

13. Step 5: Draw a line
perpendicular from 𝐵 to 𝑂.
Step 6: Set the compass on 𝐴 and set
its width to the length of 𝐴𝐵 which is
4 cm.
Example 2: Construct a square having 4
cm as length of each side.

14. Step 7: Using point A make an arc above 𝐴 and using point 𝐵 make an
arc above 𝐵, label it 𝐶.
Example 2: Construct a square having 4
cm as length of each side.

15. Step 8: Move the compass to 𝐶 and
make an arc on the left of 𝐶, then
label it 𝐷
Step 9: Connect points C and D;
points D and A.
Example 2: Construct a square having 4
cm as length of each side.

16. CONSTRUCT
A REGULAR POLYGON

17. Construct a regular pentagon with 6 cm
as the length of each side.
Step 1: Draw 𝐴𝐵̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ with length 6 cm.

18. Construct a regular pentagon with 6 cm
as the length of each side.
Step 2: Draw 108º angles at 𝐴 and 𝐵.

19. Construct a regular pentagon with 6 cm
as the length of each side.
 Step 3: Mark 6 cm on these sides and label 𝐸 and 𝐶.

20. Construct a regular pentagon with 6 cm
as the length of each side.
 Step 4: Draw 6 cm arcs using 𝐸 and 𝐶 as the
centers. Mark the point as 𝐷.

21. Construct a regular pentagon with 6 cm
as the length of each side.
 Step 5: Connect the points 𝐷 and 𝐸; 𝐶 and 𝐷.

22. Triangle
Construct a scalene triangle
such that 𝐷𝐸̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = 3 𝑐𝑚, 𝐸𝐹̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = 7 𝑐𝑚
and 𝐷𝐹̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = 5 𝑐𝑚. Label it △ 𝐷𝐸𝐹.

23. Square and Rectangle
 Construct a square having 8 cm as the length of each side
 Construct a rectangle having 3 cm as the length and 2 cm as the
width by following the steps given below.
Step 1: Draw 𝐴𝐵̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ of 3 cm.
Step 2: Construct 90⁰ angle at 𝐴 and 𝐵.
Step 3: Draw arcs of radius 2 cm from 𝐴 and 𝐵 to cut the rays
respectively at 𝐷 and 𝐶.
Step 4: Connect points 𝐶 and 𝐷 to obtain ▭𝐴𝐵𝐶𝐷.

24. Regular Pentagon and Hexagon
Construct a regular pentagon given 4
cm as the length of each side.
Construct a regular hexagon given
points 𝐴,𝐵, 𝐶,𝐷,𝐸 𝑎𝑛𝑑 𝐹 having 4 cm
as the length of each side.

25. Read and construct the following:
 1. Construct a square having 5 cm as the length of each
side.
 2. Construct a regular pentagon given 6 cm as the length
of each side.
 3. Construct a regular hexagon given points H,O, R,S,E 𝑎
𝑛𝑑 U having 4 cm as the length of each side.
 4. Construct △ SME such that SM̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = 5 𝑐𝑚,ME̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = 8 𝑐𝑚 and
SE̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ = 7 𝑐𝑚

26. Look at your surroundings and
observe everything. In a long
bond paper, draw an object
that shows the shape of:
1. Triangle
2. Square
3. Rectangle
4. Regular pentagon
5. Regular hexagon.
 Make it attractive
and creative

27. Construct a Square

28. Construct a Rectangle

29. Construct a Pentagon

30. Construct a Pentagon

31. On a separate sheet of paper, match the correct answer in
column B. Write only the letter of your answer in the
space provided.
Column A Column B
1. Find the sum of the measures of the a. 9000
vertex angles for octagon. b. 9
2. Find the sum of the measures of the c. 1,0800
vertex angles for hexagon d. 13
3. Find the sum of the measures of the e. 7200
vertex angles for heptagon f. 1,2600
4. Find the number of sides of the
regular polygon when the sum of the
measures of the vertex angle is 1,2600
5. Find the number of sides of the
regular polygon when the sum of the
measures of the vertex angle is 1,980

32. Construct the following in
a separate sheet of paper.
1. A triangle whose sides have
lengths 2.5cm and 3cm with an
included angle of 30º.
2. A rectangle whose length is equal
to 3cm and width equal to 2.5cm.
3. A regular pentagon whose side
equal to 2.7cm.
4. A regular hexagon whose sides
equal to 3.5cm