Makalah ini membahas beberapa aplikasi graf termasuk lintasan terpendek dan algoritmanya. Lintasan terpendek adalah masalah pencarian jalur dengan bobot total minimum antara dua titik dalam graf. Algoritma seperti Dijkstra dan greedy dapat digunakan untuk menemukan lintasan terpendek dengan cara memilih sisi berbobot minimum secara berurutan.

1. MATEMATIKA DISKRIT
Beberapa Aplikasi Graf/ Graf
DISUSUN OLEH:
MINTARSIH (13110381)
SITI KHOTIJAH (13110385)
IFSI- S1
DOSEN PEMBIMBING:
H. DADI ROSADI, M.KOM
STIMIK MARDIRA INDONESIA
2014

2. KATA PENGANTAR
Puji syukur kehadirat Allah SWT dengan segala kerahmatannya kami
masih diberikan kesehatan serta kesempatan dalam menyusun tugas
makalah matematika diskrit. Dalam hal ini saya sangat puas dengan hasil
dan bahan yang sudah saya siapkan sebelumnya. Makalah ini membahas
tentang materi matematika diskrit yaitu beberapa aplikasi graf. Graf
sangat erat kaitannya dengan kehidupan sehari-hari kita. Misalnya pada
sebuah jalan, ataupun pada rambu-rambu lalu lintas. Graf sendiri
mempunyai persoalan yang unik, salah satunya pada lintasan terpendek
(shortest path). Graf yang digunakan dalam pencarian lintasan terpendek
adalah graf berbobot (weight graph). Ada juga persoalan pedagang
keliling (Travelling Sales Person Problem) dan Persoalan Tukang pos Cina
( Chinese Postman Problem). Disini juga kami menyajikan algoritma
dalam graf dan pembahasannya. Semoga tugas ini dapat menambah
wawasan saya serta pembacanya juga sekaligus menambah nilai pada
perkuliaan kami.Matematika diskrit merupakan mata kuliah yang
fundamental dalam pendidikan ilmu komputer atau teknik informatika.
Saat ini matematika diskrit merupakan mata kuliah wajib pada program
pendidikan yang termasuk ke dalam kelompok teknologi informasi.
Bandung, 06 Juni 2014
Penyusun

3. BAB I LATAR BELAKANG
Matematika merupakan suatu bidang ilmu yang banyak digunakan untuk
menyelesaikan berbagai permasalahan yang muncul dalam kehidupansehari-
hari. Berbagai permasalahan tersebut ada yang dapat di modelkan kedalam
suatu model matematika namun ada pula beberapa permasalahan yang tidak
dapat dimodelkan ke dalam model matematika.
Masalah di luar bidang matematika biasanya akan dibawa ke dalam penyelesaian
matematika, yaitu dengan mencari model matematikanya. Suatu permasalahan
akan semakin mudah dipelajari, dipahami dan diselesaikan jika dapat
dimodelkan ke dalam suatu model matematika .
Setelah diperoleh model matematika dari suatu masalah, maka masalah
tersebut akan dibawa ke dalam cabang-cabang ilmu matematika untuk
menentukan penyelesaiannya. Salah satu cabang ilmu matematika yang dapat
digunakan untuk menyelesaikan permasalahan tersebut adalah teori
graph.Graph G terdiri dari himpunan tak kosong dari elemen-elemen yang
disebut titik (vertex) dan daftar pasangan berurutan dari elemen-elemen yang
disebut sisi (edge).
Himpunan titik dari graph G disebut himpunan titik dari G dinyatakan dengan
V(G) dan daftar sisi dari G dinyatakan dengan E(G). SuatuGraph G = (V,E)
menyatakan graph G dengan himpunan titik-titik V(G) dan himpunan sisi
E(G).Terdapat banyak konsep dalam graph, salah satunya adalah lintasan
terpendek (Shortest Path) yang merupakan salah satu topik yang mampu
mendukung penerapan graph dalam berbagai bidang ilmu.

4. BAB II KAJIAN TEORI DAN PEMBAHASAN
A.LINTASAN TERPENDEK (SHORTEST PATH)
Penentuan lintasan terpendek dari satu titik ke titikyang lain adalah masalah
yang sering ditemui dalam
kehidupan sehari-hari. Berbagai kalangan menemui permasalahan serupa
dengan variasi yang berbeda, contohnya seorang pengemudi yang mencari
jalurterpendek dari tempat asal ke tempat tujuan,pengantar pesanan makanan
cepat saji yang jugamencari jalur terpendek dari tempat asal ke tempat tujuan,
dan juga seorang desainer jaringan komputeryang harus mendesain skema
perutean pada jaringanyang dia tangani agar memaksimalkan performajaringan
dan meminimalkan beban yang harusditangani oleh jaringan tersebut.Seiring
dengan waktu yang berjalan dan jugaperkembangan ilmu pengetahuan dan
teknologi,
permasalahan pencarian lintasan terpendek ini telah terpecahkan dengan
berbagai algoritma. Beberapa algoritma populer yang memecahkan persoalan
pencarian lintasan terpendek tersebut adalah algoritma Dijkstra, Bellman-Ford,
A-star, FloydWarshall,dsb.
Konsep Dasar Graph
Teori Graph merupakan salah satu cabang ilmu matematika yang sering
diterpakan dan dimanfaatkan dalam kehidupan sehari-hari, ada beberapa contoh

5. permasalahan yang bisa diselesaikan dengan menggunakan teori
Graph.Contohnya pembahasan ini menyangkut pada LINTASAN TERPENDEK
(SHORTEST PATH). Permasalahan di atas dapat dibentuk sebagai graph yang
digambarkan dengan titik dan garis. Garis yang menghubungkan titik pada
graph tersebut disebut titik.
Lintasan terpendek merupakan salah satu masalah yang dapat diselesaikan
dengan menggunakan graph. Jika diberikan sebuah graph berbobot, masalah
lintasan terpendek adalah bagaimana kita mencarisebuah jalur pada graph yang
meminimumkan jumlah bobot sisi pembentuk jalur tersebut. Terdapat
bermacam persoalan lintasan terpendek antara lain:
1. Lintasan terpendek antara dua buah simpul tertentu (a pair shortestpath).
2. Lintasan terpendek antara semua pasanggan simpul (all pairs
shortestpath)
3. Lintasan terpendek dari simpul tertentu ke semua simpul yang lain(single-
source shortest path).
4. Lintasan terpendek antara dua buah simpul yang melalui beberapasimpul
tertentu (intermediate shortest path).
1. ALGORITMA-ALGORITMA LINTASAN TERPENDEK(SHORTEST PATH)
a. ALGORITMA GREEDY

6. Algoritma Greedy adalah algoritma yang memecahkan masalah langkah demi
langkah, pada setiap langkah dilakukan dengan cara:
Mengambil pilihan yang terbaik yang dapat diperoleh saat itu
Berharap bahwa dengan memilih optimum local pada setiaplangkah akan
mencapai optimum global.
Langkah-langkah algoritma greedy:
1. Menentukan titik awal dan titik tujuan, misalnya titik awal a.
2. Periksa semua sisi yang langsung bersisian dengan titik a. Pilih sisi yang
bobotnya terkecil. Sisi ini menjadi lintasan terpendek pertama, sebut saja
L(1).
3. Tentukan lintasan terpendek kedua dengan cara berikut:
4. Hitung: d(i) = panjang L(1) + bobot sisi dari simpul akhir L(1) kesimpul i
yang lain.
5. Pilih d(i) yang terkecil.
6. Bandingkan d(i) dengan bobot sisi (a, i). Jika bobot sisi (a, i) lebihkecil
daripada d(i), maka L(2) = L(1) U (sisi dari simpul akhir L(i)ke simpul i)
7. Dengan cara yang sama, ulangi langkah 2 untuk menentukanlintasan
terpendek berikutnya.
Kelebihan algoritma Greedy:
Prinsip pencarian lintasan terpendek memakai fungsi ” Seleksi” dan itu berguna
untuk menentukan jalan tersingkat untuk menuju suatu tempat. Sehingga, kita
dapat sampai tepat waktu menuju tempat tujuan.Hasil analisis berdasarkan
bobot-bobot yang berbeda, menunjukkan bahwa semakin banyak bobot yang
diberikan, maka semakin akurat pula data yang dihasilkan.Sehingga
menghasilkan waktu yang efisien.
Kekurangan algoritma Greedy:
Algoritma greedy tidak beroperasi secara menyeluruh terhadap semua alternatif
solusi yang ada (sebagaimana pada metode exhaustive search).
oPemilihan fungsi Seleksi: Mungkin saja terdapat beberapa fungsi Seleksi yang
berbeda, sehingga kita harus memilih fungsi yang tepat jika kita ingin algoritma
bekerja dengan benar dan menghasilkan solusiyang benar-benar optimum.
Karena itu, pada sebagian masalah algoritma greedy tidak selalu berhasil

7. memberikan solusi yang benar-benar optimum.
Contoh :Permasalahan :
“Carilah jalur terpendek dari titik kuning ke titik biru”
Pilihan awal yang dipilih algoritma adalah a karena a lebih pendek daripada d.
Pilihan selanjutnya hanya satu sehingga tidak ada pilihan lain selain b. Lalu ke c
dan ke tujuan akhir. Maka jaraknya adalah 10,5. Padahal jika menggunakan
jalur satu lagi sebesar 7.Begitu seterusnya Jika jarak a ke b adalah
1000.Algoritma ini tidak bisa mundur, sehingga memilih b.
Padahal nilainya sangat besar.Disanalah kelemahan algoritma ini.Tetapi dengan
tidak pernah mundur ke tempat awal untuk mencari jalan alternatif.Algoritma ini
cepat dalam menyelesain pencarian lintasan tercepat.
b. ALGORITMA DIJKSTRA
Algoritma Dijkstra ditemukan oleh Edsger Dijkstra pada tahun 1959, adalah

8. algoritma pencarian graf yang memecahkan masalah jalur terpendek yang
bersumber dari satu simpul untuk sebuah graf dengan bobot simpul tidak boleh
negatif [6]. Analisis dilakukan dengan cara memeriksa simpul dengan bobot
terkecil dan memasukkannya ke dalam himpunan solusi dengan awal pencarian
simpul asal membutuhkan pengetahuan tentang semua jalur dan bobotnya,
sehingga dibutuhkan pertukaran informasi dengan semua simpul. Algoritma
dijkstra memiliki sifat yang sederhana dan lempeng (straightforward), sesuai
dengan prinsip kerja greedy. Algoritma greedy adalah algoritma yang
memecahkan masalah langkah demi langkah, pada setiap langkah:
1. Mengambil pilihan yang terbaik yang dapat diperoleh saat itu
2. Berharap bahwa dengan memilih optimum lokal pada setiap langkah akan
mencapai optimum global. Algoritma greedy mengasumsikan bahwa optimum
lokal merupakan bagian dari optimum global [7].
Algoritma dijkstra dapat menyelesaikan jalur terpendek dari sebuah titik asal
dan titik tujuan dalam suatu graf berbobot . Jarak terpendek diperoleh dari dua
buah titik jika total bobot dari semua simpul dalam jaringan graf adalah yang
paling minimal.
Sebelum meneruskan lebih lanjut perlu diketahui beberapa notasi yang
digunakan:
1. l(i,j) : panjang jarak antara simpul i ke simpul j
2. a : titik awal pencarian
3. dai : jarak yang dikenal terpendek dan bersifat permanen dari titik awal ke
titik (i) dalam suatu jaringan.
4. qi : titik terdahulu yang dikenal terpendek dari titik awal ke titik (i) dalam
suatu jaringan.
5. c : titik terakhir yang telah pindah ke keadaan permanen.
Langkah prosedural algoritma dijkstra sebagai berikut :
1. Proses dimulai dari titik awal (a), daa. Maka titik yang satu-satunya permanen
adalah titik a. Dan titik lain berlabel sementara yang diisi dengan inisial tak
hingga (.
2. Memeriksa cabang titik yang keluar dari titik terakhir yang bersifat permanen
dengan persamaan dengan persamaan :

9. dai=min[dai,dac-l(c,i)] (1)
3. Menentukan titik mana yang akan lulus dari label sementara menjadi label
permanen. Dengan cara membandingkan nilai titik dari hasil langkah kedua dan
diambil nilai titik paling minimum. Kemudian untuk mengetahui nilai titik
permanen terdahulu, masukkan kedalam persamaan:
[dai-l(i,j)]=...dai (2)
4. Setelah mendapatkan titik dengan nilai paling minimum, maka titik yang
bernilai minimum tersebut ditetapkan sebagai titik permanen berikutnya.
5. Jika masih terdapat titik yang belum berlabel permanen maka ulangi kembali
dari langkah 2.
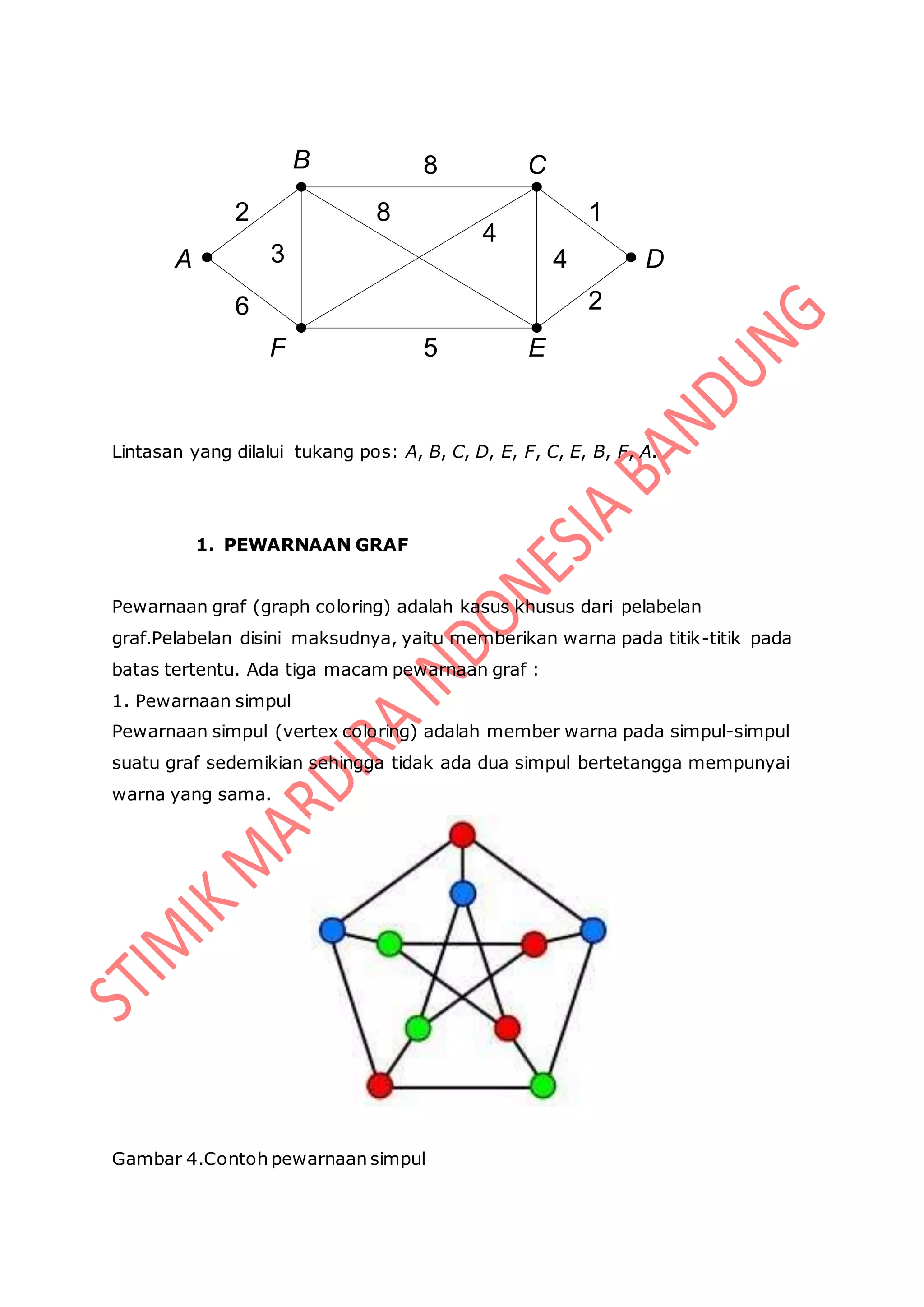
Di bawah ini diberikan contoh sebuah graf tak berarah yang terdiri dari 5 buah
titik dan 7 buah jalur yang menghubungkan antar dua buah titik. Algoritma
djikstra digunakan untuk mencari jarak terpendek dari sebuah titik ke titik
lainnya pada graf tak berarah tersebut.
Gambar 1: Contoh graf tak berarah
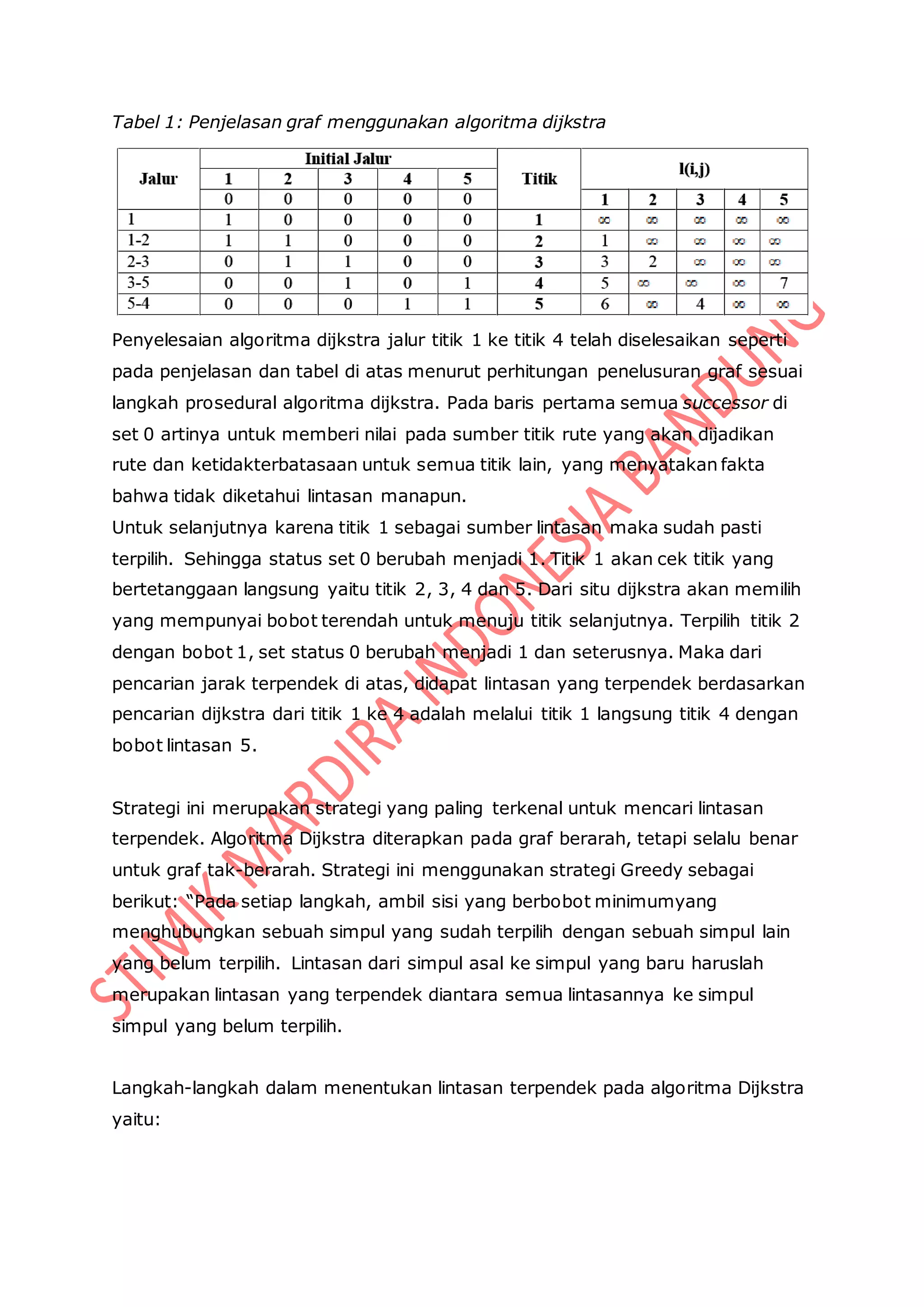
Berdasarkan contoh graf tak berarah di atas ditentukan titik awal pencarian
adalah titik 1 dengan tujuan yaitu titik 4 dan akan dicari jarak terpendek yang
dapat ditempuh dari titik 1 untuk menuju titik 4. Berikut ini tabel penjelasan graf
menggunakan algoritma dijkstra:

10. Tabel 1: Penjelasan graf menggunakan algoritma dijkstra
Penyelesaian algoritma dijkstra jalur titik 1 ke titik 4 telah diselesaikan seperti
pada penjelasan dan tabel di atas menurut perhitungan penelusuran graf sesuai
langkah prosedural algoritma dijkstra. Pada baris pertama semua successor di
set 0 artinya untuk memberi nilai pada sumber titik rute yang akan dijadikan
rute dan ketidakterbatasaan untuk semua titik lain, yang menyatakan fakta
bahwa tidak diketahui lintasan manapun.
Untuk selanjutnya karena titik 1 sebagai sumber lintasan maka sudah pasti
terpilih. Sehingga status set 0 berubah menjadi 1. Titik 1 akan cek titik yang
bertetanggaan langsung yaitu titik 2, 3, 4 dan 5. Dari situ dijkstra akan memilih
yang mempunyai bobot terendah untuk menuju titik selanjutnya. Terpilih titik 2
dengan bobot 1, set status 0 berubah menjadi 1 dan seterusnya. Maka dari
pencarian jarak terpendek di atas, didapat lintasan yang terpendek berdasarkan
pencarian dijkstra dari titik 1 ke 4 adalah melalui titik 1 langsung titik 4 dengan
bobot lintasan 5.
Strategi ini merupakan strategi yang paling terkenal untuk mencari lintasan
terpendek. Algoritma Dijkstra diterapkan pada graf berarah, tetapi selalu benar
untuk graf tak-berarah. Strategi ini menggunakan strategi Greedy sebagai
berikut: “Pada setiap langkah, ambil sisi yang berbobot minimumyang
menghubungkan sebuah simpul yang sudah terpilih dengan sebuah simpul lain
yang belum terpilih. Lintasan dari simpul asal ke simpul yang baru haruslah
merupakan lintasan yang terpendek diantara semua lintasannya ke simpul
simpul yang belum terpilih.
Langkah-langkah dalam menentukan lintasan terpendek pada algoritma Dijkstra
yaitu:

11. 1. Pada awalnya pilih titik dengan bobot yang terendah dari titik yang belum
terpilih, diinisialisasikan dengan „0‟ dan yang sudah terpilih
diinisialisasikan dengan „1‟.
2. Bentuk tabel yang terdiri dari titik, status, bobot dan redecessor. Lengkapi
kolom bobot yang diperoleh dari jarak titik sumber kesemua titik yang
langsung terhubung dengan titik sumber tersebut.
3. Jika titik sumber ditemukan maka tetapkan sebagai titik terpilih.
4. Tetapkan titik terpilih dengan label permanen dan perbarui titik yang
langsung terhubung.
5. Tentukan titik sementara yang terubung pada titik yang sudahterpilih
sebelumnya dan merupakan bobot terkecil dilihat dari tabeldan tentukan
sebagai titik terpilih berikutnya.
6. Apakah titik yang tepilih merupakan titik tujuan? Jika ya, makakumpulan
titik terpilih atau predecessor merupakan rangkaian yangmenunjukkan
lintasan terpendek.
7. Begitu seterusnya sampai semua titik terpilih.
Contoh :
Dari graph diatas tenetukan lintasan terpendek dari titik A ke titik F.
Dengan menggunakan program, diperoleh lintasan terpendek dari titk A ketitik F
sebagai berikut .Diperoleh lintasan terpendek yaitu A-E-D-F dengan bobot total
sebesar 22.
(Mencari lintasan terpendek dari simpul a ke semua simpul lain }
Langkah 0 (inisialisasi):
- inisialisasi si = 0 dan di = mai untuk i = 1, 2, ..., n

12. Langkah 1:
- isi sa dengan 1 (karena simpul a adalah simpul asal lintasan terpendek, jadi
sudah pasti terpilih)
- isi da dengan ¥ (tidak ada lintasan terpendek dari simpul a ke a)
Langkah 2, 3, ..., n-1:
- cari j sedemikian sehingga sj = 0 dan dj = min{d1, d2, ..., dn}
- isi sj dengan 1
- perbarui di, untuk i = 1, 2, 3, …, n dengan:
di (baru) = min{di (lama), dj + mji }.
Tentukan lintasan terpendek dari simpul 1 ke semua simpul lain.

13. Jadi, lintasan terpendek dari:
 1 ke 3 adalah 1, 3 dengan panjang = 10
 1 ke 4 adalah 1, 3, 4 dengan jarak = 25
 1 ke 2 adalah 1, 3, 4, 2 dengan jarak = 45
 1 ke 5 adalah 1, 5 dengan jarak = 45
 1 ke 6 tidak ada
Contoh 6.34. Tinjau graf berarah pada Gambar 6.50 yang menyatakan jarak
beberapa kota di Amerika Serikat.
Tentukan lintasan terpendek dari simpul 5 ke semua simpul lain.

14. Jadi, lintasan terpendek dari:
 5 ke 6 adalah 5, 6 dengan panjang = 250
 5 ke 7 adalah 5, 6, 7 dengan jarak = 1150
 5 ke 4 adalah 5, 6, 4 dengan jarak = 1250
 5 ke 8 adalah 5, 6, 8 dengan jarak = 1650
 5 ke 3 adalah 5, 6, 4, 3 dengan jarak = 2450
 5 ke 2 adalah 5, 6, 4, 3, 2 dengan jarak = 3250
 5 ke 1 adalah 5, 6, 8, 1 dengan jarak = 3350
 Pencarian rute terpendek merupakan salah satu persoalan dalam teori
graf. Persoalan ini bisa diselesaikan dengan algoritma dijkstra karena
lebih mudah dan menarik,
 Adapun beberapa keuntungan yang kita peroleh dari Algoritma Dijkstra
yaitu :
 1. Algoritma Dijkstra dapat menentukan jalur tercepat dengan waktu
yang lebih cepat dibandingkan algoritma lainnya.
 2. Menggunakan Algoritma Dijkstra mempermudah kita dalam
mengetahui jarak atau lintasan terpendek dari suatu titik tertentu ke
semua titik yang lain.
 3. Menggunakan Algoritma Dijkstra dalam penerapan di dalam sistem
geografis akan menampilakan visualisasi data dalam bentuk peta
 4. Pada penampilan rute atau peta Algoritma Dijkstra lebih mudah di
baca dan di pahami.

15.  5. Pada rute atau peta dan lintasannya dapat diberikan warna, sehingga
penampilan Algoritma Dijkstra lebih menarik dan lebih mudah untuk
membedakan dari suatu titik tertentu ke titik yang lain.
c. ALGORITMA BELLMAN-FORD
Algoritma Bellman-Ford merupakan algoritma untuk mencari shortest path,
dengan menghitung jarak terpendek pada sebuah graf berbobot, atau
menghitung semua jarak terpendek yang berawal dari satu titik node. Langkah-
langkah:
1. Tentukan vertex source dan daftar seluruh vertices maupun edges.
2. Assign nilai untuk distance dari vertex source = 0, dan yang lain infinite
3. Mulailah iterasi terhadap semua vertices yang dimulai dari Vertexsource
4. Untuk menentukan distance dari semua vertices yang
berhubungandengan vertex source dengan formula seperti berikut ini :- U
= vertex asal- V = vertex tujuan- UV = Edges yang menghubungkan U
dan V- Jika distance V, lebih kecil dari distance U + weight UV maka
distance V, diisi dengan distance U + weight UV- Lakukan hingga semua
vertex terjelajahi
5. Untuk mengecek apakah ada negative cycle dalam graf tersebut lakukan
iterasi untuk semua edges yang ada, kemudia lakukan penge-cek-an
seperti dibawah ini :

16. 6. Untuk semua edges UV, jika ada distance vertex U + weight edges
UVkurang dari distance vertex V maka sudah jelas bahwa graf
tersebutmemiliki negative cycle.
Contoh:Dari graph di atas tentukan lintasan terpendek dari titik 1 ke titik 4.
Langkah-langkah:
1. Tahap pertama adalah tahap inisialisasi yaitu dengan melabeli titik awal
atau titik asal yaitu titik 1 dengan 0 dan titik-titik lainnya dengan
∞.d(1,1)< 0 untuk masing-masing v anggota V – {s} maka d(s,v)< ∞
2. Tahap kedua yaitu tahap proses iterasiUntuk masing-masing sisi (1,2)
anggota E makaJika d(1,2) > d(1,2)+w(2,3) makad(1,2)diganti dengan
d(1,2)+w(2,3)Akhirnya diperoleh d(1,4)=5+4+4=13.
Langkah Algoritma
Algoritma ini, seperti algoritma djikstra menggunakan tepi relaksasi tetapi tidak
memakai metode greedy. Bahkan, ini menggunakan d[u] sebagai batas atas
pada jarak d[u,v] dari u ke v. Algortima ini secara berkala mengurangi perkiraan
d[v] pada bobot dari jalan terpendek dari sumber verteks s ke tiap verteks v
pada V hingga memperoleh jalan terpendek. Berikut ini penulis melampirkan
langkah-langkah penyusunan algoritmanya yang akan mengembalikan nilai

17. TRUE jika pada graf tidak terdapat siklus yang negatif dan akan mengembalikan
nilai FALSE jika sebaliknya.
BELLMAN-FORD (G, w, s)
1. INITIALIZE-SINGLE-SOURCE (G, s)
2. for each vertex i = 1 to V[G] - 1 do
3. for each edge (u, v) in E[G] do
4. RELAX (u, v, w)
5. For each edge (u, v) in E[G] do
6. if d[u] + w(u, v) < d[v] then
7. return FALSE
8. return TRUE
Inisialisasi pada line 1 memerlukan waktu O(v) time. Untuk loop dari line 2-4
memerlukan waktu O(E) dan untuk line 5-7 memerlukan O(E) time pula. Jadi,
Bellman-Ford berjalan dalam kompleksitas waktu O(E) time.
Pseudocode Algoritma Bellman-Ford
Gambar 1. Pseudocode menurut Wikipedia
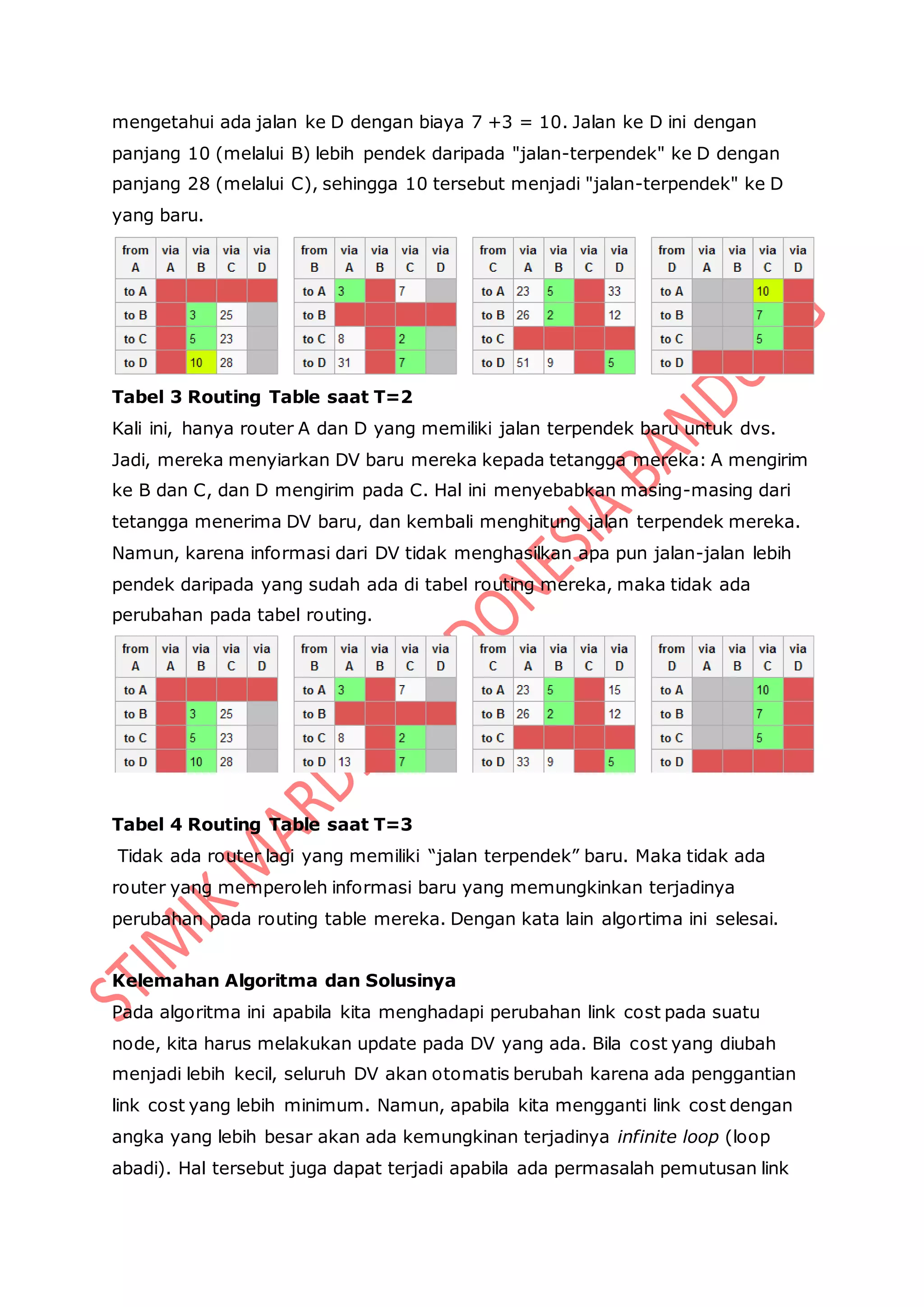
Penulis menandai waktu saat ini (atau iterasi) dalam algoritma dengan T, dan
akan mulai (pada waktu 0, atau T = 0) dengan membuat matriks jarak untuk
setiap router ke tetangga terdekatnya. tabel routing di bawah ini, jalan

18. terpendek akan disorot dengan warna hijau, dan update untuk jalan terpendek
baru disorot dengan warna kuning.
Tabel 1 Routing Table saat T=0
Pada titik ini, semua router (A, B, C, D) memiliki "jalan-terpendek" untuk DV
mereka (daftar jarak yang berasal dari mereka ke router lain melalui tetangga).
Mereka masing-masing mengirimkan DV baru ini kepada semua tetangga
mereka: A ke B dan C, B ke C dan A, C ke A, B, dan D, dan D ke C. tetangga
masing-masing menerima informasi ini, kemudian menghitung ulang yang jalur
terpendek digunakannya. Sebagai contoh: A menerima sebuah DV dari C yang
menyatakan A ada jalur melalui C ke D, dengan jarak (atau biaya) 5. Karena
saat ini "jalan terpendek" ke C adalah 23, maka A tahu itu jalan ke D bahwa
biaya 23 +5 = 28. Karena tidak ada jalan lain yang lebih pendek yang diketahui
A, ia menempatkan ini sebagai perkiraan arus-jalan terpendek dari dirinya
sendiri (A) ke D, via C.
Tabel 2 Routing Table saat T=1
Sekali lagi, semua router telah diperoleh dalam iterasi terakhir (pada T = 1)
"jalan terpendek", sehingga mereka semua menyiarkan DV mereka pada
tetangga mereka; Hal ini mendorong masing-masing tetangga untuk kembali
menghitung jarak terpendek mereka lagi. Sebagai contoh: A menerima sebuah
DV dari B yang memberitahu A ada jalur melalui B ke D, dengan jarak (atau
biaya) dari 7. Karena saat ini "jalan-terpendek" untuk B adalah 3, maka A

19. mengetahui ada jalan ke D dengan biaya 7 +3 = 10. Jalan ke D ini dengan
panjang 10 (melalui B) lebih pendek daripada "jalan-terpendek" ke D dengan
panjang 28 (melalui C), sehingga 10 tersebut menjadi "jalan-terpendek" ke D
yang baru.
Tabel 3 Routing Table saat T=2
Kali ini, hanya router A dan D yang memiliki jalan terpendek baru untuk dvs.
Jadi, mereka menyiarkan DV baru mereka kepada tetangga mereka: A mengirim
ke B dan C, dan D mengirim pada C. Hal ini menyebabkan masing-masing dari
tetangga menerima DV baru, dan kembali menghitung jalan terpendek mereka.
Namun, karena informasi dari DV tidak menghasilkan apa pun jalan-jalan lebih
pendek daripada yang sudah ada di tabel routing mereka, maka tidak ada
perubahan pada tabel routing.
Tabel 4 Routing Table saat T=3
Tidak ada router lagi yang memiliki “jalan terpendek” baru. Maka tidak ada
router yang memperoleh informasi baru yang memungkinkan terjadinya
perubahan pada routing table mereka. Dengan kata lain algortima ini selesai.
Kelemahan Algoritma dan Solusinya
Pada algoritma ini apabila kita menghadapi perubahan link cost pada suatu
node, kita harus melakukan update pada DV yang ada. Bila cost yang diubah
menjadi lebih kecil, seluruh DV akan otomatis berubah karena ada penggantian
link cost yang lebih minimum. Namun, apabila kita mengganti link cost dengan
angka yang lebih besar akan ada kemungkinan terjadinya infinite loop (loop
abadi). Hal tersebut juga dapat terjadi apabila ada permasalah pemutusan link

20. dari suatu node dengan mengganti bobot linknya menjadi 999. Berikut
penjelasan secara rincinya dengan contoh berikut.
Gambar 3. Kasus pada Router A, B, C
Pada mulanya routing table yang terbentuk di A adalah A-B = 3 A-C = 5
sedangkan di B adalah B-A = 3
B-C = 2
dan di C adalah C-A = 5
C-B = 2
Gambar 4. Seakan-akan Ada Path pada Router A-C, C-A
Hal ini akan terus berlangsung selama tidak terjadi perubahan. Bila terjadi
proses update link cost antara B dan C menjadi 1.
Gambar 5. Update Cost pada Router B-C menjadi 1 Maka B akan
mengirimkan paket ke tetangganya (A, C) bahwa ada jalan baru dari B-C
dengan cost 1. Karena C memiliki cost dari C-B dengan bobot minimum 2,
sedangkan ada update dari B bahwa ada jalan yang melalui B-C dengan bobot 1
(di mana 1 < 2), C akan mengganti cost “jalan-terpendek” dari C-B menjadi 1.
Dan hal ini mempengaruhi Kemudian router A yang tadinya memiliki cost link
antara A-C yang sebelumnya bernilai 5, mendapat informasi dari B bahwa ada
path baru dari B-C dengan nilai 1, ia akan mengganti cost A-C yang sebelumnya
5 dengan 3+1=4, karena 4 < 5. Sehingga kini routing table yang terbentuk di A
adalah A-B = 3 A-C = 4 sedangkan di B adalah B-A = 3
B-C = 1
dan di C adalah C-A = 4

21. C-B = 1
Gambar 6. Distance Cost yang Baru
Namun hal tersebut akan berdampak buruk apabila penggantian cost tersebut
melebihi pseudo path yang terbentuk pada node A-C. Misalkan kita mematikan
link antara B-C dan mengesetnya menjadi 999.
Gambar 7. Link Antara B-C Diset Menjadi 999
Hal pertama yang dilakukan router B adalah mengubah cost dari B-C menjadi
999. routing table yang terbentuk di A adalah tetap A-B = 3 A-C = 4 sedangkan
di B adalah B-A = 3 B-C = 999 dan di C pun ikut mengganti bobot path C-B C-A
= 4 C-B = 999. Tetapi ketika router B akan mengirimkan paket update kepada
tetangganya, router A dan C akan mengirimkan paket DV mereka terlebih
dahulu di mana masih terdapat pseudo-path antara A-C dengan bobot 4. B yang
mengetahui hal ini akan memilih jalur B-A-C dengan bobot 3+4=7 karena lebih
kecil dari 999. B akan mengganti path yang ia miliki menjadi 7.
B-A = 3
B-C = 7
Setelah itu barulah router A berubah menjadi
A-B = 3
A-C = 999
Router C kini telah terputus
Gambar 8. Perubahan Link Hasil Update

22. Masalah tersebut belum berhenti karena sebelum B sempat mengganti link cost
ke C miliknya menjadi 999, A telah menerima update bahwa ada link cost antara
B-C yang bernilai 7, sehingga A akan menemukan jalan bahwa ternyata ada
jalan ke router C yang lebih minimum melalui A-B-C sebesar 3+7=10, (10 <
999) sehingga router A akan mengganti cost “jalan-terpendek”nya menjadi A-B
= 3
A-C = 10
Setelah itu barulah router B berubah menjadi B-A = 3
B-C = 999
Gambar 9. Perubahan Selanjutnya
Dan hal ini kan berlangsung secara terus menerus hingga kedua sisi mencapai
angka maksimum putus yaitu 999. Hal inilah yang dikatakan sebagai infinite
loop.
Gambar 10. Kondisi Akhir
Untungnya, hal tersebut dapat diatasi dengan menggunakan perintah untuk
melakukan Bellman-Ford ulang setiap kali ada perubahan link cost. Kita dapat
menggunakan boolean UPDATE yang bernilai FALSE saat awal dan bernilai TRUE
bila ada perubahan link cost yang terjadi. Setiap kita melakukan update link cost
kita akan mengeset boolean UPDATE menjadi TRUE. Apabila boolean UPDATE
bernilai TRUE, seluruh router wajib melakukan Bellman-Ford ulang dari susunan
toplogy router yang baru, oleh sebab itu kita perlu mencatat link cost antar
tetangga terbaru yang ada pada setiap router. Apabila kita melakukan Bellman-
Ford ulang, otomatis masalah mengenai perubahan cost dari B-C di atas tidak
akan berpengaruh sebab sejak awal C sudah dianggap telah down dan tidak
diperhitungkan dalam algoritma ini.
d .Algoritma Floyd Warshall

23. Algoritma Floyd Warshall adalah salah satu varian dari pemrograman dinamis,
metode untuk memecahkan masalah pencarian rute terpendek (sama seperti
Algoritma Dijkstra).
Metode ini melakukan pemecahan masalah dengan memandang solusi yang
akan diperoleh sebagai suatu keputusan yang saling terkait. Maksudnya, solusi-
solusi dibentuk dari solusi yang berasal dari tahap sebelumnya dan ada
kemungkinan solusi lebih dari satu.
Algoritma ini juga bisa diterapkan pada sebuah aplikasi pencari rute jalan yang
terdekat dari suatu daerah ke daerah lainnya.dengan metode ini hasil yang di
dapat bisa lebih optimal namun memelukan resource yang cukup besar jika
dipakai untuk pencarian yang kompleks.
Sebagai contoh adalah mencari rute terpendek dari titik A menuju titik Cdari
grafik berikut :
Langkah pertama kita jadikan grafik di atas menjadi sebuah tabel atau matriks.

24. Kotak abjad berwarna hijau disamping kiri adalah titik awal dan kotak abjad
berwarna merah yang ada di atas adalah titik tujuan-nya. Sedangkan kotak
angka hijau dan merah berfungsi untuk menentukan sebuah index
proses (R0=1,R1=2,R2=3,dan R3=4) dan memudahkan posisi angka-angka
yang ada didalam tabel dengan mengkombinasikan-nya dengan kotak abjad
yang sama dengan warnaya. sebagai contoh :
A(3),B(2) (titik awal, titik tujuan) = 9,0
Karena dalam grafik diatas terdapat 4 buah titik, yaitu A, B, C, D maka akan
ada 5 proses yang akan dilewati yaitu R0, R1, R2, R3, dan R4 sebagai hasil
akhir. perlu diingat bahwa hasil dari sebuah proses akan digunakan untuk proses
berikutnya.
Rumusnya adalah :
r = Index proses. =>R0 = 1, R1 = 2, R2 = 3, R3 = 4, R4 adalah hasil akhir.
S = Titik awal. => A, B, C, dan D (kotak hijau).
E = Titik tujuan. => A, B, C, dan D (kotak merah).
" jika hasil penjumlahan nilai titik awal S(r) dan nilai titik tujuan E(r) lebih kecil
daripada nilai jarak yang sebenarnya S(E), maka ganti nilai jarak sebenarnya

25. dengan hasil penjumlahan nilai titik awal dan nilai titik tujuan [ S(E) = S(r) +
E(r) ] ".
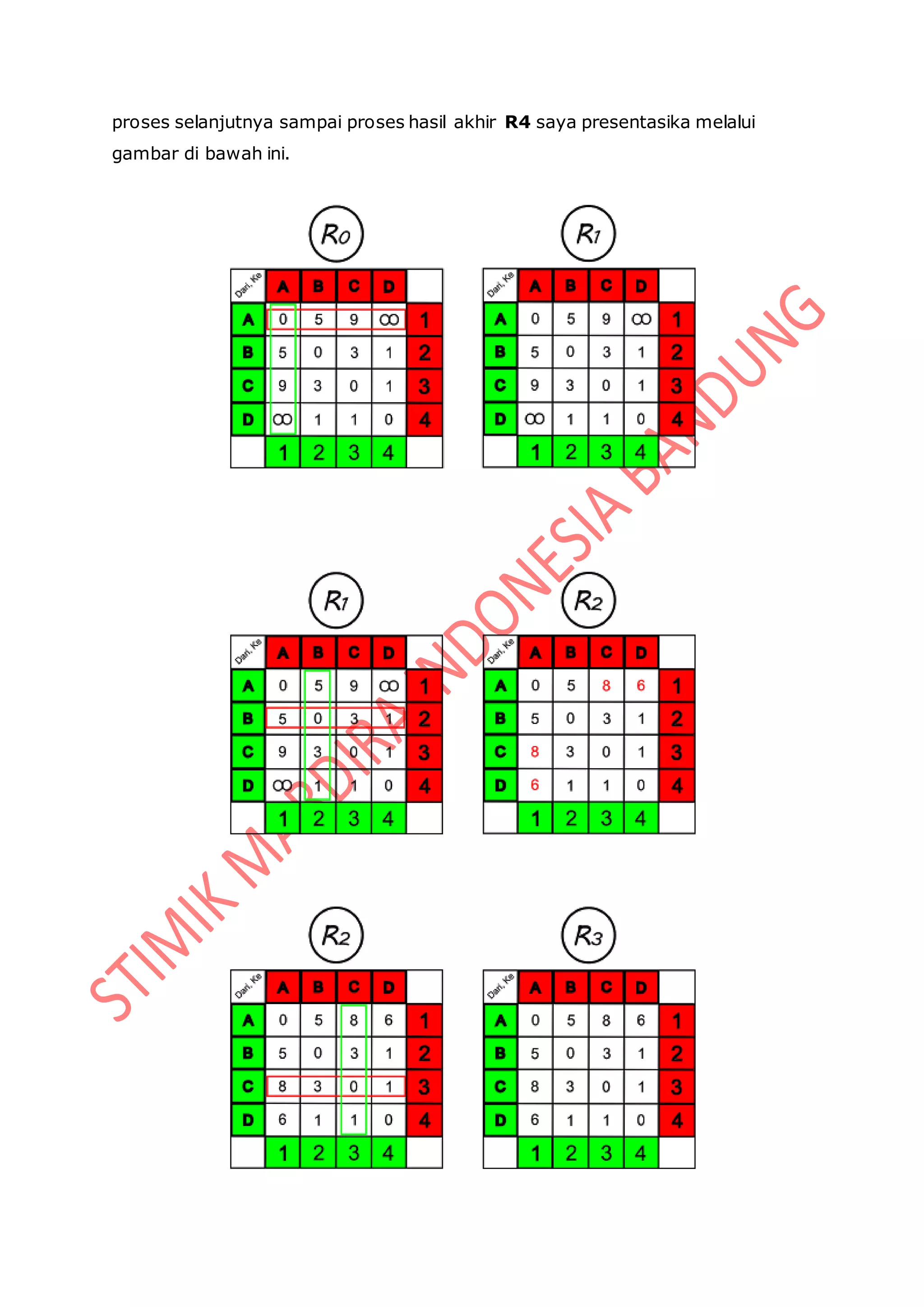
Jadi, Saya akan mencontohkan sebagian penerapan rumus diatas untuk proses
pertama yaitu R0.
r = R0 = 1
S = { A(r) = 0 ; B(r) = 5 ; C(r) = 9 ; D(r) = tak hingga}
E = { A(r) = 0 ; B(r) = 5 ; C(r) = 9 ; D(r) = tak hingga}
- Titik awal A ke titik tujuan A => A(A) = 0
A(r) + A(r) = 0 + 0 = 0 => 0 sama dengan
A(A) <tidak diganti>
- Titik awal A ke titik tujuan B =>A(B) = 5
A(r) + B(r) = 0 + 5 = 5 => 5 sama dengan A(B)
<tidak diganti>
- Titik awal A ke titik tujuan C => A(C) = 9
A(r) + C(r) = 0 + 9 = 9 => 9 sama
dengan A(C) <tidak diganti>
- Titik awal A ke titik tujuan C => A(D) = tak hingga
A(r) + D(r) = 0 + tak hinggga = tak hingga => tak hingga sama
dengan A(D) <tidak diganti>
- Titik awal B ke titik tujuan A => B(A) = 5
B(r) + A(r) = 5 + 0 = 5 => 0 sama
dengan B(A) <tidak diganti>
- Titik awal B ke titik tujuan B => B(B) = 0
B(r) + B(r) = 5 + 5 = 10 => 10 lebih
besar dari B(B) <tidak diganti>
- Titik awal B ke titik tujuan C => B(C) = 3
B(r) + C(r) = 5 + 9 = 14 => 14 lebih

26. besar dari B(C) <tidak diganti>
- Titik awal B ke titik tujuan C => B(D) = 1
B(r) + D(r) = 5 + tak hinggga = tak hingga => tak hingga lebih
besar dari B(D) <tidak diganti>
- Titik awal C ke titik tujuan A => C(A) = 9
C(r) + A(r) = 9 + 0 = 9 => 9 sama
dengan C(A) <tidak diganti>
- Titik awal C ke titik tujuan B => C(B) = 3
C(r) + B(r) = 9 + 5 = 14 => 14 lebih
besar dari C(B) <tidak diganti>
- Titik awal C ke titik tujuan C => C(C) = 0
C(r) + C(r) = 9 + 9 = 18 => 18 lebih
besar dari C(C) <tidak diganti>
- Titik awal C ke titik tujuan C => C(D) = 1
C(r) + D(r) = 9 + tak hinggga = tak hingga => tak hingga lebih
besar dari C(D) <tidak diganti>
- Titik awal D ke titik tujuan A => D(A) = tak hingga
D(r) + A(r) = tak hingga + 0 = tak hingga => tak
hingga sama dengan D(A) <tidak diganti>
- Titik awal D ke titik tujuan B => D(B) = 1
D(r) + B(r) = tak hingga + 5 = tak hingga => tak
hingga lebih besar dari D(B) <tidak diganti>
- Titik awal D ke titik tujuan C => D(C) = 1
D(r) + C(r) = tak hingga + 9 = tak hingga => tak
hingga lebih besar dari D(C) <tidak diganti>
- Titik awal D ke titik tujuan C => D(D) = 0
D(r) + D(r) = tak hingga + tak hinggga = tak hingga => tak
hingga lebih besar dari D(D) <tidak diganti>
Demikianlah proses dari R0. Tidak ada yang diganti karna tidak ada hasil
penjumlahan yang menunjukkan lebih dari nilai jarak sebenarnya S(E). Untuk

27. proses selanjutnya sampai proses hasil akhir R4 saya presentasika melalui
gambar di bawah ini.

28. Dari hasil tabel matriks R4 dapat diketahui rute terpendek manakah yang harus
ditempuh dari titik Amenuju ke titik C. kemudian kita tulis nilai-nilai yang ada di
table matriks R4 disamping titik dalam grafik sesuai dengan abjab mereka.
KESIMPULAN
1. Algoritma Greedy
Dengan menggunakan algoritma greedy didapatkan bobot total
sebesar13,38 km, tetapi hasil ini tidak optimal karena dengan
menggunakan algoritma yang lain didapatkan hasil dengan jarak yang
lebih pendek.Algoritma ini memiliki kelebihan yaitu cepat dalam proses
pencarianlintasan terpendeknya. Sedangkan kekurangannya yaitu tidak

29. optimal danada kemungkinan gagal dalam pencarian dan mungkin
lintasan yang diperoleh bukanlah yang terpendek.
2. Algoritma Dijkstra
Dalam algoritma dijkstra juga menggunakan prinsip greedy yang
menyatakan bahwa pada setiap langkah kita memilih sisi yang berbobot
minimum dan memasukannya kedalam himpunan solusi.Selain itu
algoritma dijkstra paling terkenal dari algoritma lainnya karena dijkstra
diterapkan mencari lintasan terpendek pada graf berarah.Namun, juga
benar untuk graf tidak berarah.
B.PERSOALAN PERJALANAN PEDAGANG (TRAVELLING SALESPERSON
PROBLEM - TSP)
Diberikan sejumlah kota dan jarak antar kota. Tentukan sirkuit terpendek yang
harus dilalui oleh seorang pedagang bila pedagang itu berangkat dari sebuah
kota asal dan menyinggahi setiap kota tepat satu kali dan kembali lagi ke kota
asal keberangkatan.
==>menentukan sirkuit Hamilton yang memiliki bobot minimum.
Aplikasi TSP:
1. Pak Pos mengambil surat di kotak pos yang tersebar pada n buah lokasi di
berbagai sudut kota.
2. Lengan robot mengencangkan n buah mur pada beberapa buah peralatan
mesin dalam sebuah jalur perakitan.
3. Produksi n komoditi berbeda dalam sebuah siklus.

30. Jumlah sirkuit Hamilton di dalam graf lengkap dengan n simpul: (n - 1)!/2.
Graf di atas memiliki (4 – 1)!/2 = 3 sirkuit Hamilton, yaitu:
I1 = (a, b, c, d, a) atau (a, d, c, b, a) ==> panjang = 10 + 12 + 8 + 15 = 45
I2 = (a, c, d, b, a) atau (a, b, d, c, a) ==> panjang = 12 + 5 + 9 + 15 = 41
I3 = (a, c, b, d, a) atau (a, d, b, c, a) ==> panjang = 10 + 5 + 9 + 8 = 32
Jadi, sirkuit Hamilton terpendek adalah I3 = (a, c, b, d, a) atau (a, d, b, c, a)
dengan panjang sirkuit = 10 + 5 + 9 + 8 = 32.
 Lintasan Hamilton ialah lintasan yang melalui tiap simpul didalam graf
tepat satu kali
 Sirkuit Hamilton ialah sirkuit yang melalui tiap simpul didalam graf tepat
satu kali, kecuali simpul awal (juga mrpk simpul akhir) dilalui 2 kali
 Graf yang memiliki sirkuit Hamilton disebut graf Hamilton , sedangkan
graf yang memiliki lintasan Hamilton disebut graf semi Hamilton
a b
c
d
12
8
15
10
9
5
a b
c
d
12
8
15
10
a b
c
d
12
15
9
5
a b
c
d
8
10
9
5

31. Contoh :
Graf Di samping memiliki lintasan
Hamilton dengan lintasan :
b,c,d,e,f,g,a,b
dan Graf di samping juga memiliki sirkuit Hamilton karena di awali di simpul b
dan berakhir di simpul b

32. Graf disamping memiliki lintasan Hamilton dengan lintasan :
a,b,c,d,e,i,f,g,h
Tapii graf disamping tidak memiliki sirkuit Hamilton
Algoritma genetika adalah algoritma komputasi yang diinspirasi teori evolusi
yang kemudian diadopsi menjadi algoritma komputasi untuk mencari solusi
suatu permasalahan dengan cara yang lebih “alamiah”. Salah satu aplikasi
algoritma genetika adalah pada permasalahan optimasi kombinasi, yaitu
mendapatkan suatu nilai solusi optimal terhadap suatu permasalahan yang
mempunyai banyak kemungkinan solusi. Dalam tulisan ini akan dibahas teori
dasar algoritma genetika beserta contoh aplikasinya dalam menyelesaikan suatu
permasalahan optimasi kombinasi sederhana.

33. 1.TEORI DASAR ALGORITMA GENETIKA
Algoritma genetika yang dikembangkan oleh Goldberg adalah algoritma
komputasi yang diinspirasi teori evolusi Darwin yang menyatakan bahwa
kelangsungan hidup suatu makhluk dipengaruhi aturan “yang kuat adalah yang
menang”. Darwin juga menyatakan bahwa kelangsungan hidup suatu makhluk
dapat dipertahankan melalui proses reproduksi, crossover, dan mutasi.
Konsep dalam teori evolusi Darwin tersebut kemudian diadopsi menjadi
algoritma komputasi untuk mencari solusi suatu permasalahan dengan cara
yang lebih “alamiah”.
Sebuah solusi yang dibangkitkan dalam algoritma genetika disebut sebagai
chromosome, sedangkan kumpulan chromosome-chromosome tersebut disebut
sebagai populasi. Sebuah chromosomedibentuk dari komponen-komponen
penyusun yang disebut sebagai gen dan nilainya dapat berupa bilangan numerik,
biner, simbol ataupun karakter tergantung dari permasalahan yang ingin
diselesaikan.
Chromosome-chromosome tersebut akan berevolusi secara berkelanjutan yang
disebut dengan generasi. Dalam tiap generasi chromosome-chromosome
tersebut dievaluasi tingkat keberhasilan nilai solusinya terhadap masalah yang
ingin diselesaikan (fungsi_objektif) menggunakan ukuran yang disebut dengan
fitness. Untuk memilih chromosome yang tetap dipertahankan untuk generasi
selanjutnya dilakukan proses yang disebut dengan seleksi. Proses seleksi
chromosome menggunakan konsep aturan evolusi Darwin yang telah disebutkan
sebelumnya yaitu chromosome yang mempunyai nilai fitness tinggi akan
memiliki peluang lebih besar untuk terpilih lagi pada generasi selanjutnya.
Chromosome-chromosome baru yang disebut dengan offspring, dibentuk
dengan cara melakukan perkawinan antar chromosome-chromosome dalam satu
generasi yang disebut sebagai proses crossover. Jumlah chromosome dalam
populasi yang mengalami crossover ditetukan oleh paramater yang disebut
dengan crossover_rate. Mekanisme perubahan susunan unsur penyusun
mahkluk hidup akibat adanya faktor alam yang disebut dengan mutasi
direpresentasikan sebagai proses berubahnya satu atau lebih nilai gen dalam
chromosome dengan suatu nilai acak. Jumlah gen dalam populasi yang
mengalami mutasi ditentukan oleh parameter yang dinamakan mutation_rate.

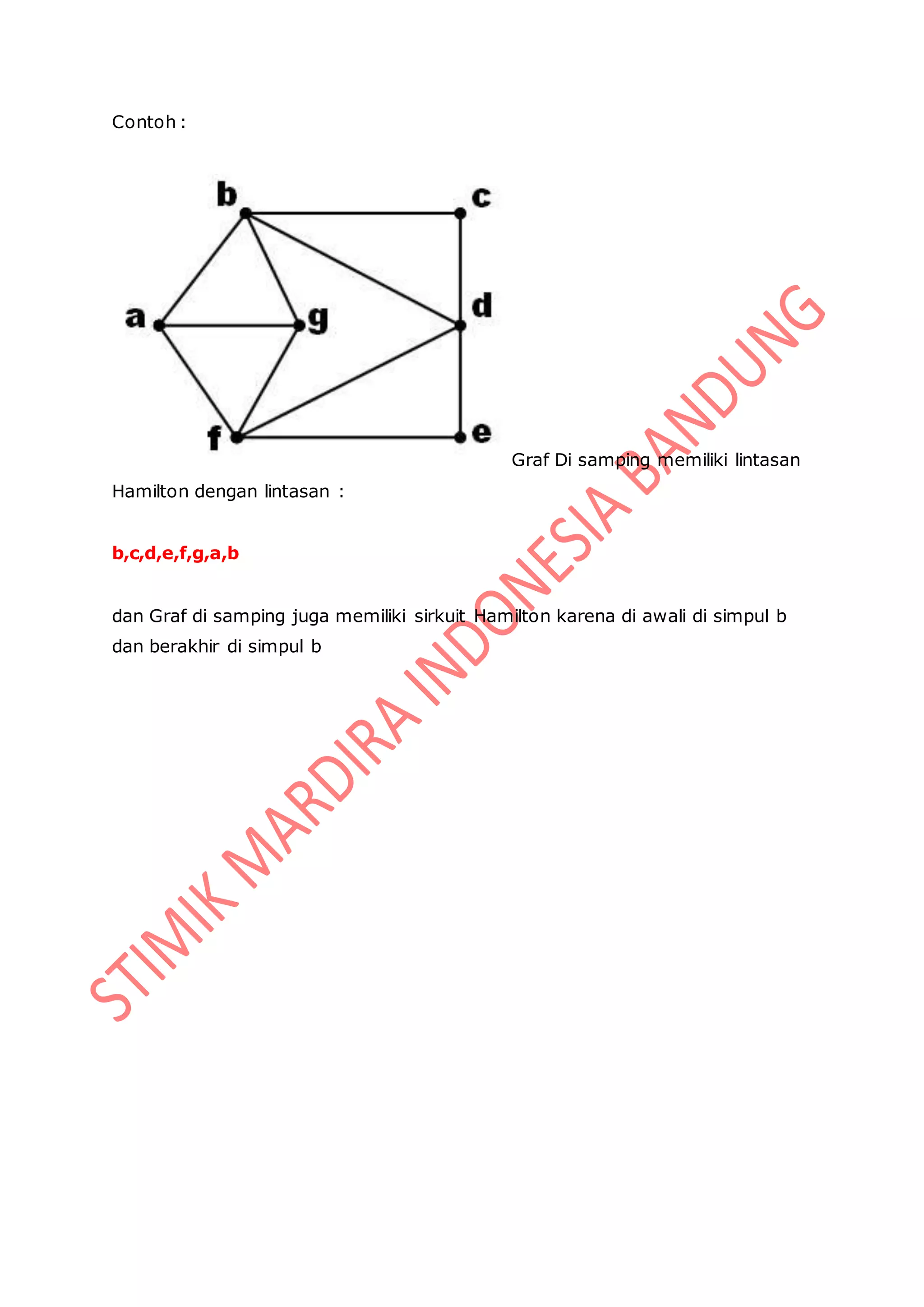
34. Setelah beberapa generasi akan dihasilkan chromosome-chromosome yang nilai
gen-gennya konvergen ke suatu nilai tertentu yang merupakan solusi terbaik
yang dihasilkan oleh algoritma genetika terhadap permasalahan yang ingin
diselesaikan.
Aplikasi Algoritma Genetika
Berikut adalah contoh aplikasi algoritma genetika yang digunakan untuk
menyelesaikan masalah kombinasi.Misalkan ada persamaan a+2b+3c+4d = 30,
kita mencari nilai a, b, c, dan d yang memenuhi persamaan diatas.Kita mencoba
menggunakan algoritma genetika untuk menyelesaikan permasalahan diatas.
Penjelasan mengenai langkah-langkah penyelesaian permasalahan diatas
menggunakan algoritma genetika adalah sebagai berikut:
1. Pembentukan chromosome
Karena yang dicari adalah nilai a, b, c, d maka variabel a, b, c, d dijadikan
sebagai gen-gen pembentuk chromosome. Batasan nilai variabel a adalah
bilangan integer 0 sampai 30. Sedangkan batasan nilai variabel b, c, dan d
adalah bilangan integer 0 sampai 10.
2. Inisialisasi
Proses inisialisasi dilakukan dengan cara memberikan nilai awal gen-gen dengan
nilai acak sesuai batasan yang telah ditentukan.
Misalkan kita tentukan jumlah populasi adalah 6, maka:
Chromosome[1] = [a;b;c;d] = [12;05;03;08]
Chromosome[2] = [a;b;c;d] = [02;01;08;03]
Chromosome[3] = [a;b;c;d] = [10;04;03;04]
Chromosome[4] = [a;b;c;d] = [20;01;10;06]
Chromosome[5] = [a;b;c;d] = [01;04;03;09]
Chromosome[6] = [a;b;c;d] = [20;05;07;01]
3. Evaluasi Chromosome
Permasalahan yang ingin diselesaikan adalah nilai variabel a, b, c, dan d yang
memenuhi persamaan a+2b+3c+4d = 30, maka fungsi_objektif yang dapat
digunakan untuk mendapatkan solusi adalah fungsi_objektif(chromosome) = |
(a+2b+3c+4d) – 30 |
Kita hitung fungsi_objektif dari chromosome yang telah dibangkitkan:
fungsi_objektif(chromosome[1])= Abs(( 12 + 2*5 + 3*3 + 4*8 ) – 30)
= Abs((12 + 10 + 9 + 32 ) – 30)
= Abs(63 – 30)

35. = 33
fungsi_objektif(chromosome[2])= Abs(( 2 + 2*1 + 3*8 + 4*3 ) – 30)
= Abs(( 2 + 2 + 24 + 12 ) – 30)
= Abs(40 – 30)
= 10
fungsi_objektif(chromosome[3])= Abs(( 10 + 2*4 + 3*3 + 4*4 ) – 30)
= Abs(( 10 + 8 + 9 + 16 ) – 30)
= Abs(43 – 30)
= 13
fungsi_objektif(chromosome[4])= Abs(( 20 + 2*1 + 3*10 + 4*6 ) – 30)
= Abs(( 20 + 2 + 30 + 24 ) – 30)
= Abs(76 – 30)
= 46
fungsi_objektif(chromosome[5])= Abs(( 1 + 2*4 + 3*3 + 4*9 ) – 30)
= Abs(( 1 + 8 + 9 + 36 ) – 30)
= Abs(54 – 30)
= 24
fungsi_objektif(chromosome[6])= Abs(( 20 + 2*5 + 3*7 + 4*1 ) – 30)
= Abs(( 20 + 10 + 21 + 4) – 30)
= Abs(55 – 30)
= 25
Rata-rata dari fungsi objektif adalah:
rata-rata = (33+10+13+46+24+25)/6
= 151 / 6
= 25.167
4. Seleksi Chromosome
Proses seleksi dilakukan dengan cara membuat chromosome yang mempunyai
fungsi_objektif kecil mempunyai kemungkinan terpilih yang besar atau
mempunyai nilai probabilitas yang tinggi. Untuk itu dapat digunakan fungsi
fitness = (1/(1+fungsi_objektif)), fungsi_objektif perlu ditambah 1 untuk
menghindari kesalahan program yang diakibatkan pembagian oleh 0.
fitness[1] = 1 / (fungsi_objektif[1]+1)
= 1 / 34
= 0.0294
fitness[2] = 1 / (fungsi_objektif[2]+1)

36. = 1 / 11
= 0.0909
fitness[3] = 1 / (fungsi_objektif[3]+1)
= 1 / 14
= 0.0714
fitness[4] = 1 / (fungsi_objektif[4]+1)
= 1 / 47
= 0.0212
fitness[5] = 1 / (fungsi_objektif[5]+1)
= 1 / 25
= 0.0400
fitness[6] = 1 / (fungsi_objektif[6]+1)
= 1 / 26
= 0.0385
total_fitness = 0.0294 + 0.0909 + 0.0714 + 0.0212 + 0.04 + 0.0385
= 0.2914
Rumus untuk mencari probabilitas: P[i] = fitness[i] / total_fitness
P[1] = 0.0294 / 0.2914
= 0.1009
P[2] = 0. 0909 / 0.2914
= 0.3119
P[3] = 0. 0714 / 0.2914
= 0.2450
P[4] = 0. 0212 / 0.2914
= 0.0728
P[5] = 0.04 / 0.2914
= 0.1373
P[6] = 0.0385 / 0.2914
= 0.1321
Dari probabilitas diatas dapat kita lihat kalau chromosome ke 2 yang mempunyai
fitness paling besar maka chromosome tersebut mempunyai probabilitas untuk
terpilih pada generasi selanjutnya lebih besar dari chromosomelainnya. Untuk
proses seleksi kita gunakan roulete wheel, untuk itu kita harus mencari dahulu
nilai kumulatif probabilitasnya:
C[1] = 0.1009

37. C[2] = 0.1009+ 0.3119
= 0.4128
C[3] = 0.1009+ 0.3119 + 0.2450
= 0.6578
C[4] = 0.1009+ 0.3119 + 0.2450 + 0.0728
= 0.7306
C[5] = 0.1009+ 0.3119 + 0.2450 + 0.0728 + 0.1373
= 0.8679
C[6] = 0.1009+ 0.3119 + 0.2450 + 0.0728 + 0.1373 + 0.1321
= 1
Setelah dihitung cumulative probabilitasnya maka proses seleksi menggunakan
roulete-wheel dapat dilakukan. Prosesnya adalah dengan membangkitkan
bilangan acak R dalam range 0-1.
Jika R[k] <C[1] maka pilih chromosome 1 sebagai induk, selain itu pilih
chromosome ke-k sebagai induk dengan syarat C[k-1] < R < C[k]. Kita putar
roulete wheel sebanyak jumlah populasi yaitu 6 kali (bangkitkan bilangan acak
R) dan pada tiap putaran, kita pilih satu chromosome untuk populasi baru.
Misal:
R[1] = 0.201
R[2] = 0.284
R[3] = 0.009
R[4] = 0.822
R[5] = 0.398
R[6] = 0.501
Angka acak pertama R[1] adalah lebih besar dari C[1] dan lebih kecil daripada
C[2] maka pilih chromosome[2] sebagai chromosome pada populasi baru, dari
bilangan acak yang telah dibangkitkan diatas maka populasi chromosome baru
hasil proses seleksi adalah:
chromosome[1] = chromosome[2]
chromosome[2] = chromosome[2]
chromosome[3] = chromosome[1]
chromosome[4] = chromosome[5]
chromosome[5] = chromosome[2]
chromosome[6] = chromosome[3]

38. Chromosome baru hasil proses seleksi:
chromosome[1] = [02;01;08;03]
chromosome[2] = [02;01;08;03]
chromosome[3] = [12;05;03;08]
chromosome[4] = [01;04;03;09]
chromosome[5] = [02;01;08;03]
chromosome[6] = [10;04;03;04]
5. Crossover
Setelah proses seleksi maka proses selanjutnya adalah proses crossover. Metode
yang digunakan salah satunya adalah one-cut point, yaitu memilih secara acak
satu posisi dalam chromosomeinduk kemudian saling menukar gen.
Chromosome yang dijadikan induk dipilih secara acak dan jumlah chromosome
yang mengalami crossover dipengaruhi oleh parameter crossover_rate ( ρc ).
Pseudo-code untuk proses crossover adalah sebagai berikut:
begin
k← 0;
while(k<populasi) do
R[k] ← random(0-1);
if (R[k] <ρc ) then
select Chromosome[k]as parent;
end;
k = k + 1;
end;
end;
Misal kita tentukan crossover probability adalah sebesar 25%, maka diharapkan
dalam satu generasi ada 50% Chromosome (3 chromosome) dari satu generasi
mengalami proses crossover. Prosesnya adalah sebagai berikut:
Pertama kita bangkitkan bilangan acak R sebanyak jumlah populasi
R[1] = 0.191
R[2] = 0.259
R[3] = 0.760
R[4] = 0.006
R[5] = 0.159
R[6] = 0.340

39. Maka Chromosomeke k akan dipilih sebagai induk jika R[k] < ρc, dari bilangan
acak R diatas maka yang dijadikan induk adalah chromosome[1],
chromosome[4] dan chromosome[5].
Setelah melakukan pemilihan induk proses selanjutnya adalah menentukan
posisi crossover. Ini dilakukan dengan cara membangkitkan bilangan acak
dengan batasan 1 sampai (panjang chromosome-1), dalam kasus ini bilangan
acak yang dibangkitkan adalah 1 – 3. Misalkan didapatkan posisi crossover
adalah 1 maka chromosome induk akan dipotong mulai gen ke 1 kemudian
potongan gen tersebut saling ditukarkan antar induk.
chromosome[1] >< chromosome[4]
chromosome[4] >< chromosome[5]
chromosome[5] >< chromosome[1]
Posisi cut-point crossover dipilih menggunakan bilangan acak 1-3 sebanyak
jumlah crossover yang terjadi, misal
C[1] = 1
C[2] = 1
C[3] = 2
offspring[1] = chromosome[1]>< chromosome[4]
= [02;01;08;03] >< [01;04;03;09]
= [02;04;03;09]
offspring[4] = Chromosome[4] >< Chromosome[5]
= [01;04;03;09] >< [02;01;08;03]
= [01;01;08;03]
offspring[5] = Chromosome[5] >< Chromosome[1]
= [02;01;08;03] >< [02;01;08;03]
= [02;01;08;03]
Dengan demikian populasi Chromosome setelah mengalami proses crossover
menjadi:
chromosome[1] = [02;04;03;09]
chromosome[2] = [02;01;08;03]
chromosome[3] = [12;05;03;08]
chromosome[4] = [01;01;08;03]
chromosome[5] = [02;01;08;03]
chromosome[6] = [10;04;03;04]

40. 6. Mutasi
Jumlah chromosome yang mengalami mutasi dalam satu populasi ditentukan
oleh parameter mutation_rate. Proses mutasi dilakukan dengan cara mengganti
satu gen yang terpilih secara acak dengan suatu nilai baru yang didapat secara
acak. Prosesnya adalah sebagai berikut.Pertama kita hitung dahulu panjang total
gen yang ada dalam satu populasi. Dalam kasus ini panjang total gen adalah
total_gen = (jumlah gen dalam chromosome) * jumlah populasi
= 4 * 6
= 24
Untuk memilih posisi gen yang mengalami mutasi dilakukan dengan cara
membangkitkan bilangan integer acak antara 1 sampai total_gen, yaitu 1
sampai 24. Jika bilangan acak yang kita bangkitkan lebih kecil daripada variabel
mutation_rate (ρm) maka pilih posisi tersebut sebagai sub-chromosome yang
mengalami mutasi. Misal ρm kita tentukan 10% maka diharapkan ada 10% dari
total_gen yang mengalami populasi:
jumlah mutasi = 0.1 * 24
= 2.4
= 2
Misalkan setelah kita bangkitkan bilangan acak terpilih posisi gen 12 dan 18
yang mengalami mutasi. Dengan demikian yang akan mengalami mutasi adalah
chromosome ke-3 gen nomor 4 dan Chromosome ke-5 gen nomor 2. Maka nilai
gen pada posisi tersebut kita ganti dengan bilangan acak 0-30.
Misalkan bilangan acak yang terbangkitkan adalah 2 dan 5. Maka populasi
chromosome setelah mengalami proses mutasi adalah:
chromosome[1] = [02;04;03;09]
chromosome[2] = [02;01;08;03]
chromosome[3] = [12;05;03;02]
chromosome[4] = [01;01;08;03]
chromosome[5] = [02;05;08;03]
chromosome[6] = [10;04;03;04]
Setelah proses mutasi maka kita telah menyelesaikan satu iterasi dalam
algoritma genetika atau disebut dengan satu generasi. Maka fungsi_objective
setelah satu generasi adalah:
chromosome[1] = [02;04;03;09]
fungsi_objektif[1] = Abs(( 2 + 2*4 + 3*3 + 4*9 ) – 30)

41. = Abs(( 2 + 8 + 9 + 36 ) – 30)
= Abs( 55 – 30)
= 25
chromosome[2] = [02;01;08;03]
fungsi_objektif[2] = Abs(( 2 + 2*1 + 3*8 + 4*3 ) – 30)
= Abs(( 2 + 2 + 24 + 12 ) – 30)
= Abs(40 – 30)
= 10
chromosome[3] = [12;05;03;02]
fungsi_objektif[3] = Abs(( 12 + 2*5 + 3*3 + 4*2 ) – 30)
= Abs(( 12 + 10 + 9 + 8 ) – 30)
= Abs(39 – 30)
= 9
chromosome[4] = [01;01;08;03]
fungsi_objektif[4] = Abs(( 1 + 2*1 + 3*8 + 4*3 ) – 30)
= Abs(( 1 + 2 + 24 + 12 ) – 30)
= Abs(39 – 30)
= 9
chromosome[5] = [02;05;08;03]
fungsi_objektif[5] = Abs(( 2 + 2*5 + 3*8 + 4*3 ) – 30)
= Abs(( 2 + 10 + 24 + 12 ) – 30)
= Abs(48 – 30)
= 18
chromosome[6] = [10;04;03;04]
fungsi_objektif[6] = Abs(( 10 + 2*4 + 3*3 + 4*4 ) – 30)
= Abs(( 10 + 8 + 9 + 16 ) – 30)
= Abs(43 – 30)
= 13
Rata-rata fungsi objektif setelah satu generasi adalah:
rata-rata = ( 25 + 10 + 9 + 9 + 18 + 13) / 6
= 84 / 6
= 14.0
Dapat dilihat dari hasil perhitungan fungsi objektif diatas bahwa setelah satu
generasi, nilai hasil rata-rata fungsi_objektif lebih menurun dibandingkan hasil
fungsi_objektif pada saat sebelum mengalami seleksi, crossover dan mutasi.Hal

42. ini menunjukkan bahwa chromosome atau solusi yang dihasilkan setelah satu
generasi lebih baik dibandingkan generasi sebelumnya. Maka pada generasi
selanjutnya chromosome-chromosome yang baru adalah:
chromosome[1] = [02;04;03;09]
chromosome[2] = [02;01;08;03]
chromosome[3] = [12;05;03;02]
chromosome[4] = [01;01;08;03]
chromosome[5] = [02;05;08;03]
chromosome[6] = [10;04;03;04]
Chromosome-chromosome ini akan mengalami proses yang sama seperti
generasi sebelumnya yaitu proses evaluasi, seleksi, crossover dan mutasi yang
kemudian akan menghasilkan chromosome-chromosome baru untuk generasi
yang selanjutnya. Proses ini akan berulang sampai sejumlah generasi yang telah
ditetapkan sebelumnya.
Setelah 50 generasi didapatkan chromosome yang terbaik adalah:
Chromosome = [07;05;03;01]
Jika didekode maka:
a=7 ; b=5 ; c=3 ; d=1
Jika dihitung terhadap persamaan f = a+2b+3c+4d:
7 + (2*5) + (3*3) + (4*1) = 30
C. Persoalan Tukang Pos Cina (Chinese Postman Problem)
Dikemukakan oleh Mei Gan (berasal dari Cina) pada tahun 1962.
Masalahnya adalah sebagai berikut: seorang tukang pos akan mengantar surat
ke alamat-alamat sepanjang jalan di suatu daerah. Bagaimana ia merencanakan
rute perjalanannya supaya ia melewati setiap jalan tepat sekali dan kembali lagi
ke tempat awal keberangkatan.
===>menentukan sirkuit Euler di dalam graf.

43. Lintasan yang dilalui tukang pos: A, B, C, D, E, F, C, E, B, F, A.
1. PEWARNAAN GRAF
Pewarnaan graf (graph coloring) adalah kasus khusus dari pelabelan
graf.Pelabelan disini maksudnya, yaitu memberikan warna pada titik-titik pada
batas tertentu. Ada tiga macam pewarnaan graf :
1. Pewarnaan simpul
Pewarnaan simpul (vertex coloring) adalah member warna pada simpul-simpul
suatu graf sedemikian sehingga tidak ada dua simpul bertetangga mempunyai
warna yang sama.
Gambar 4.Contoh pewarnaan simpul
B C
E
F
8
5
3
A D
8
2
1
6
4
4
2

44. 2. Pewarnaan sisi
Pewarnaan sisi (edge coloring) adalah memberi warnaberbeda pada sisi yang
bertetangga sehingga tidak ada dua sisi yang bertetangga mempunyai warna
yang sama.
Gambar 5.Contoh pewarnaan sisi
3. Pewarnaan bidang
Pewarnaan bidang adalah memberi warna pada bidang sehingga tidak ada
bidang yang bertetangga mempunyai warna yang sama. Pewarnaan bidang
hanya bisa dilakukan dengan membuat graf tersebut menjadi graf planar
terlebih dahulu.Graf planar adalah graf yang dapat digambarkan pada bidang
datar dengan sisi-sisi yang tidak saling memotong (bersilangan), seperti yang
ditunjukkan gambar di bawah ini.
Gambar 6.Contoh Grraf Planar

45. Setelah terbentuk graf planar, lalu memberikan warna berbeda untuk setiap
bidang yang berdekatan.Dan jumlah warna yang digunakan harus sedikit
mungkin.
Gambar 7.Contoh pewarnaan bidang
Dalam pewarnaan graf, jumlah warna yang digunakan untuk mewarnai simpul,
sisi, maupun bidang diusahakan sesedikit mungkin. Jumlah warna minimum
yang dapat digunakan tersebut disebut bilangan kromatik graf G, disimbolkan
dengan χ(G). Suatu graf G yang mempunyai bilangan kromatis k dilambangkan
dengan χ(G) = k.
PENGATURAN WARNA PADA LAMPU LALU LINTAS MENGGUNAKAN GRAF
Sudah disebutkan sebelumnya bahwa sampai saat ini, teori graf masih
diterapkan di berbagai persoalan dalam kehidupan sehari-hari.Misalnya aplikasi
pewarnaan graf dalam pengaturan warna lampu lalu lintas di perempatan jalan
sehingga mencegah terjadinya tabrakan di perempatan jalan tersebut.

46. Gambar 8.Lampu lalu lintas perempatan jalan
Seperti yang ditunjukkan pada gambar diatas, sebuah perempatan jalan
mempunyai 4 buah lampu lalu lintas.Lampu lalu lintas pada jalan B dan F
menyala bersamaan.Lampu lalu lintas pada jalan D dan H juga menyala
bersamaan. Dalam perempatan jalan tersebut diketahui jika lampu di jalan B
dan F menyala hijau maka jalur yang boleh digunakan adalah dari B ke E, F ke
A. selain itu jalur langsung belok kiri juga diperbolehkan, yaitu dari B ke C, dan
F ke G. Jika di jalan D dan H lampu hijau menyala maka jalur yang boleh
digunakan untuk melintas adalah jalur dari D ke E, D ke G, H ke A, dan H ke C.
Dalam kondisi ini, jalur langsung belok kiri juga diperoblehkan. Untuk
menyelesaikan permasalahan pada pembuatan lampu lalu lintas pada sebuah
perempatan jalan, maka hal yang harus dilakukan terlebih dahulu adalah
menentukan jalur mana yang bisa berjalan dengan member lampu hijau di
tempat tertentu dan member lampu merah agar kendaraan pada lintasan yang
lain berhenti sehingga tidak terjadi tabrakan.

47. Gambar 9. Jalur di perempatan jalan
Diketahui bahwa jalur yang bisa digunakan untuk melintas adalah dari B ke C, B
ke E, D ke E, D ke G, F ke G, F ke A, H ke A, dan H ke C. Setelah mengetahui
jalur mana saja yang bisa dilewati, berikut langkah-langkah untuk mengatur
lampu lalu lintas menggunakan graf.
1. Membuat simpul-simpul sebagai tanda dari semua jalur yang bisa dilewati
dalam perempatan jalan. Letak dari simpul-simpul tersebut bebas, tidak ada
aturan tertentu untuk mengharuskan simpul harus diletakkan di posisi mana
karena hal itu tidak terlalu berpengaruh.

48. Gambar 10.Simpul-simpul dari jalur jalan
2.Menentukan sisi untuk menghubungkan 2 simpul yang saling melintas atau
berseberangan. Untuk memudahkan hal ini, carilah simpul-simpul yang
menunjukkan jalur mana saja yang akan bertabrakan jika semua lampu lalu
lintas berwarna hijau. Pada Gambar 9 terlihat bahwa jalur BE dan DG, BE dan
HC, FA dan DG, FA dan HC saling berseberangan. Karena BE dan DG
berseberangan, maka kedua simpul tersebut dihubungkan dengan garis yang
disebut sisi.Setelah itu, simpul-simpul lain yang saling berseberangan juga
dihubungkan dengan sebuah sisi.
Gambar 11.Graf jalur jalan
3. Setelah menghubungkan semua simpul (jalur) yang saling berseberangan,
langkah selanjutnya yang harus dilakukan adalah memberi warna pada masing-
masing simpul dengan ketentuan pemberian warnanya sebagai berikut :
• Menggunakan jumlah warna sedikit mungkin
• Simpul yang bertetanggaan (terhubung dengan sisi) tidak boleh berwarna
sama
• Memberi warna yang sama pada simpul yang tidak terhubung secara langsung
• Simpul yang tidak terhubung dengan sisi (simpul terpencil), berarti jalur
tersebut boleh berlaku lampu lalu lintas berwarna hijau terus.
• Warna yang digunakan bebas.

49. Gambar 12.Pewarnaan pada simpul graf
Berdasarkan gambar diatas, semua simpul telah diwarnai sesuai ketentuan
pewarnaan pada graf.
Graf diatas memiliki bilangan kromatis 3 (χ(G) = 3) karena jumlah minimum
warna yang digunakan sebanyak 3. Simpul FA dan BE berwarna sama yaitu hijau
karena keduanya tidak terhubung/bertetanggaan. Tapi simpul DG dan HC
terhubung dengan simpul FA dan BE sehingga harus diberi warna yang berbeda
yaitu warna merah. Sementara simpul HA, BC, DE, FG diberi warna sama yaitu
kuning karena simpul-simpul tersebut adalah simpul terpencil yang tidak
terhubung dengan simpul lain dan itu berarti bahwa jalur-jalur dari simpul
tersebut tidak ada yang saling melintas sehingga keempat jalur itu bisa berlaku
lampu hijau terus.
4. Langkah selanjutnya adalah mengelompokkan simpul-simpul tersebut
berdasarkan kesamaan warna.
• Merah = DG dan HC
• Hijau = BE dan FA
• Kuning = BC, DE, FG, dan HA
Dari pengelompokkan tersebut diperoleh 2 kondisi untuk lampu lalu lintas di
perempatan jalan.
Lampu Merah = DG, HC
Lampu Hijau = BE, FA, BC, DE, FG, HA
Tabel 1. Kondisi lampu lalu lintas 1
Lampu Merah = BE, FA
Lampu Hijau = DG, HC, BC, DE, FG, HA

50. Tabel 2. Kondisi lampu lalu lintas 2
Berdasarkan tabel-tabel diatas, lampu merah berarti bahwa jalur tidak boleh
digunakan untuk melintas, sedangkan lampu hijau menunjukkan bahwa jalur
bisa digunakan untuk melintas. Pada Tabel 1, jika di jalan D dan H lampu merah
menyala maka jalur DG dan HC tidak boleh digunakan. Disaat yang bersamaan
di jalan B dan F lampu hijau menyala sehingga jalur BE dan FA boleh digunakan.
Karena langsung belok kiri juga diperbolehkan, maka jalur BC, DE, FG, HA juga
bisa digunakan untuk melintas. Hal-hal tersebut juga berlaku untuk Tabel 2,
ketika di jalan B dan F lampu merah menyala maka di jalan D dan H lampu hijau
akan menyala. Sehingga jalur-jalur yang bisa digunakan antara lain DG, HC, BC,
DE, FG, dan HA.
PENYUSUNAN JADWAL DENGAN METODE PEWARNAAN GRAF
Salah satu aplikasi penerapan pewarnaan graf dalam kehidupan sehari-hari
adalah dalam penyusunan sebuah jadwal.Sebuah jadwal yang ada mula-mula
dipetakan menjadi bentuk graf terlebih dahulu. Proses pewarnaan graf ini
nantinya akan dilakukan pada graf yang terbentuk. Pemetaan dilakukan dengan
mengasumsikan bahwa setiap jadwal adalah sebuah vertex (simpul) dan urutan
jadwal atau dua jadwal yang tidak bisa diadakan bersamaan dipetakan dengan
membuat edge(sisi) antara dua titik tersebut. Untuk kapasitas ruang yang ada
akan dimodelkan dengan batasan jumlah warna sama yang bisa digunakan
untuk mewarnai simpul. Setelah proses pewarnaan graf telah selesai, setiap
simpul pada graf hasil pewarnaan tersebut akan memiliki warna sama yang
berbeda-beda. Dari warnawarna tersebut akan diketahui bahwa simpul dengan
warna yang sama bisa dijadwalkan bersamaan sedangkan untuk simpul dengan
warna yang berlainan harus dijadwalkan berbeda. Jumlah warna yang digunakan
menunjukkan banyaknya jadwal yang harus disusun dalam melakukan
penyusunan jadwal. Karena penulis adalah seorang mahasiswa, disini penulis
akan mengambil contoh bagaimana menyusun jadwal kuliah dengan metode
pewarnaan graf ini. Misalkan terdapat himpunan delapan orang mahasiswa,
M= {1, 2, 3, 4, .., 8}
Dan lima buah mata kuliah yang dapat dipilih oleh kedelapan mahasiwa
tersebut,
MK= {1, 2, 3, 4, 5}

51. Tabel berikut memperlihatkan matriks lima mata kuliah dan delapan orang
mahasiswa.
Tabel 1. Tabel Mata Kuliah yang Diambil Oleh Delapan Orang Mahasiswa
Pada tabel tersebut terlihat matriks lima mata kuliah dan delapan orang
mahasiwa. Angka 1 pada elemen (i, j) menandakan bahwa mahasiwa I memilih
mata kuliah j, sedangkan angka 0 menyatakan bahwa mahasiswa tersebut tidak
memilih mata kuliah j. Berdasarkan tabel tersebut, akan ditentukan sebuah
jadwal ujian sedemikian sehingga semua mahasiwa dapat mengikuti semua
ujian mata kuliah tersebut. Oleh karena itu tidak boleh terdapat jadwal ujian
mata kuliah yang bertabrakan dengan jadwal ujian mata kuliah lainnya yang
juga diambil oleh mahasiswa tersebut. Ujian dua buah mata kuliah dapat
dijadwalkan pada waktu yang sama jika tidak ada mahasiwa yang sama yang
mengikuti ujian dua mata kuliah tersebut. Penyelesaian untuk masalah ini sama
dengan persoalan menentukan bilangan kromatik untuk sebuh graf. Pertama-
tama, persoalan tersebut dipetakan ke dalam sebuah graf, diman setiap simpul
dalam graf tersebut menyatakan mata kuliah.Dan sisi yang menghubungkan dua
simpul menyatakan ada mahasiwa yang memilih kedua mata kuliah tersebut.

52. Gambar 3: Graf Mata Kuliah Delapan Orang Mahasiswa
Dapat dilihat pada graf tersebut bahwa apabila terdapat dua buah simpul yang
dihungkan oleh kedua sisi, maka ujian kedua mata kuliah tersebut tidak
dapatdiadakan secara bersamaan. Simpul (mata kuliah) tidak boleh mendapat
alokasi waktu (warna simpul) yang sama.Warna-warna yang berbeda dapat
diberikan kepada simpul-simpul graf tersebut.Jadwal yang efisien adalah jadwal
yang memungkinkan waktu sedikit mungkin untuk melaksanakan semua
kegiatan tersebut. Oleh karena itu, disini yang akan dicari adalah bilangan
kromatik graf tersebut, χ(G). Dalam mengerjakan pewarnaan graf ini, dapat
menggunakan langkah-langkah pewarnaan graf secara umum ataupun
algoritma. Semua cara tergantung kepada individu yang akan menyusun sebuah
jadwal itu sendiri. Pada graf persoalan diatas, ditemukan bahwa bilangan
kromatik graf tersebut adalah dua.Oleh karena itu simpul pada graf tersebut
dapat diwarnai oleh dua macam warna yang menandakan bahwa ujian-ujian
kelima mata kuliah tersebut dapat dilaksanakan hanya pada dua waktu
saja.Berikut merupakan gambar graf persoalan ini yang telah diberi warna.

53. Gambar 4: Graf yang Telah Diberi Warna Tiap Simpulnya
Pada gambar diatas, terlihat bahwa ujian untuk mata kuliah A, D, dan E dapat
dilaksanakan pada waktu yang bersamaan, begitu pula dengan mata kuliah B
dan C. Perbedaan warna simpul menunjukkan bahwa ujian mata kuliah tersebut
dilaksanakan pada waktu yang berbeda.
Contoh lainnya adalah dalam menyusun sebuah jadwal rapat.Misalkan terdapat
tugas kelompok.Dalam satu kelas tedapat enam buah kelopokmahasiswa.Satu
mahasiswa dapat bergabung ke dalam kelompok lainnya juga.
Berikut merupakan daftar nama tiap-tiap kelompok.
K1= {Amir, Budi, Yanti}
K2= {Budi, Hasan, Tommy}
K3= {Amir, Tommy, Yanti}
K4= {Hasan, Tommy, Yanti}
K5= {Amir, Budi}
K6= {Budi, Tommy, Yanti}
Disini persoalan yang akan dipecahkan adalah bagaimana menyusun jadwal
asistensi untuk tiap kelompok agar tidak saling bertabrakan. Hal yang pertama
dilakukan adalah memetakan persoalan tersebut ke dalam graf seperti yang
diperlihatkan pada graf berikut.
Gambar 5: Graf Persoalan Jadwal Asistensi

54. Pada graf tersebut, tiap simpul menandakan tiap kelompok dan sisi menandakan
kelompok yang memiliki anggota kelopoknya yang sama. Dengan menggunakan
metode pewarnaan graf, diperoleh bilangan kromatik graf tersebut adalah 5.Oleh
karean itu, gambar graf yang telah diwarnai tiap simpulnya adalah sebagai
berikut.
Gambar 6: Graf Persoalan Jadwal Asistensi yang Telah Diberi Warna Tiap
Simpulnya
Dari gambar diatas dapat terlihat bahwa untuk menyelesaikan masalah jadwal
asistensi, jadwal asistensi dapat dilakukan pada lima waktu yang berbeda. Dari
contoh-contoh yang telah dijabarkan diatas.Telah dijabarkan beberapa contoh
penyelesaian permasalahan penyusunan jadwaldengan metode pewarnaan
graf.Untuk graf dengan jumlah simpul yang sedikit, dapat ditentukan bilangan
kromatik suatu graf dengan mudah. Namun untuk graf dengan jumlah simpul
yang banyak, disini diperlukan sebuah software computer

55. DAFTAR PUSTAKA
http://rahadikusuma.blogspot.com/2014/01/matenatika-diskrit-lintasan-
terpendek.html
http://siraith.files.wordpress.com/2009/10/matematika-deskrit-graf.pdf
http://id.wikipedia.org/wiki/Lintasan_Hamilton
http://sutikno.blog.undip.ac.id/files/2011/11/3-Algen-TSP.pdf
http://pakrudi.files.wordpress.com/2011/02/teori-graf.pdf
http://www.scribd.com/doc/95725710/Makalah-Graf-Jalur-Angkot
http://informatika.stei.itb.ac.id/~rinaldi.munir/Matdis/2011-
2012/Makalah2011/Makalah-IF2091-2011-057.pdf
http://lecturer.eepis-
its.edu/~entin/Kecerdasan%20Buatan/Buku/Bab%207%20Algoritma%20Geneti
ka.pdf
http://achmad-asrori.blogspot.com/2013/01/algoritma-floyd-warshall.html
http://achmad-asrori.blogspot.com/2013/01/algoritma-floyd-warshall.html
http://achmad-asrori.blogspot.com/2013/01/algoritma-dijkstra.html
http://pakrudi.files.wordpress.com/2011/02/teori-graf.pdf
http://informatika.stei.itb.ac.id/~rinaldi.munir/Matdis/2006-
2007/Makalah/Makalah0607-106.pdf
http://rahadikusuma.blogspot.com
http://www.google.co.id/url?sa=t&rct=j&q=&esrc=s&source=web&cd=2&ved=0
CCwQFjAB&url=http%3A%2F%2Finformatika.stei.itb.ac.id%2F~rinaldi.munir%2
FStmik%2F2009-2010%2FMakalah2009%2FMakalahIF3051-2009-
044.pdf&ei=G22SU_DpB9agugS73oLQCw&usg=AFQjCNFomlNyVj3wumHfjFsG8Z
bKCm830g&bvm=bv.68445247,d.c2E
http://www.google.co.id/url?sa=t&rct=j&q=&esrc=s&source=web&cd=6&cad=rj
a&uact=8&ved=0CEwQFjAF&url=http%3A%2F%2Feprints.dinus.ac.id%2F5180
%2F1%2FP6-TI24-SEMANTIK-80_Farida_Ardiani-
UII_Yogjakarta.pdf&ei=jWmSU-2dM8SLuASq6ILADQ&usg=AFQjCNGGq8w-
L5SmskVSicIoDbD0IGEAyg&bvm=bv.68445247,d.c2E