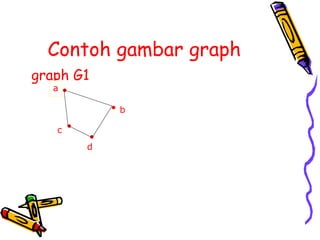
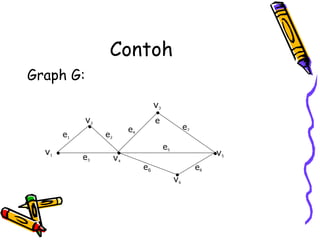
Dokumen ini menjelaskan teori graph, termasuk definisi dan jenis-jenis graph seperti graph sederhana, graph komplit, graph bipartisi, dan konsep penting seperti lintasan, siklus, dan derajat titik. Juga dibahas adalah contoh-contoh dan aplikasi dari teori ini dalam menyelesaikan masalah tertentu. Selain itu, dokumen ini menjelaskan kondisi isomorfisme antar graph dan karakteristik dari graph terhubung serta pohon.

1. TEORI GRAPH Def: Sebuah graph G adalah pasangan terurut dari (V(G), E(G)) V(G) = Himpunan obyek berhingga dan takkosong = Himpunan titik (Vertex-set) E(G) = Himpunan obyek berhingga dan mungkin kosong dg syarat setiap anggota E(G) merupakan pasangan tak berurutan dari titik di V(G). = Himpunan sisi (edge-set)

2. Contoh Graph 1. G = (V(G), E(G)) graph V(G) = {a, b, c, d} E(G) = {{a, b}, {a, c}, {b, d}, {c, d}} 2. {{a, b, c}, {{a, a}, {a, b}, {a, b}} bukan graph krn bukan pasangan berurutan 3. ({a, b, c}, {{a, a}, {a, b}, {a, b}}) graph 4. ({1, 2, 3}, {{1, 2}, {3, 4}})bukan graph krn 4 bukan anggota V(G) tetapi 4 muncul di E(G)

3. Contoh gambar graph graph G1 ● ● ● ● a c b d

4. KONSEP DALAM GRAPH Loop (gelung)=sisi dalam graph G yang menghubungkan titik v dengan dirinya sendiri. Sisi rangkap (Multiple edges)= terdapat lebih dari sebuah sisi yang menghubungkan dua titik Graph sederhana (simple graph)=sebuah graph yang tidak memiliki loop dan tidak memiliki sisi rangkap Graph rangkap (Multi graph)=sebuah graph yang tidak memiliki loop tetapi memiliki sisi rangkap Graph komplit (complete graph)=graph sederhana yang mana untuk setiap dua titik dari titik-titiknya dihubungkan oleh sebuah sisi Graph kosong (empty graph)=graph yang tidak memiliki sisi

5. KONSEP DALAM GRAPH Graph bipartisi (bipartite graph)=jika titik-titiknya dapat dipartisi menjadi dua himpunan bagian A dan B sedemikian hingga setiap sisi di graph tersebut menghubungkan sebuah titik di A dan sebuah titik di B Graph bipartisi komplit (complete bipartite graph)=graph sederhana dan bipartisi dg partisi (A, B) sedemikian hingga setiap titik di A berhubungan langsung dg setiap titik di B Graph bagian (sub graph)=H G, jika V(H) V(G) dan E(H) E(G) Graph bagian rentang (spaning sub graph)= H G dan V(H)=V(G)

6. Contoh permasalahan Misalkan ada 10 center akan dibangun canel dengan syarat tiap dua center dihubungkan dengan 1 canel dan tidak ada canel yang dihubungkan dari suatu center ke dirinya sendiri. Maka ada berapa maksimal canel yang dibuat? Berapa minimal canel yang dibuat sedemikian hingga setiap center dapat dihubungkan ke center lain?

7. Dua graph G dan H isomorfik, ditulis G ∞H, bila: Terdapat korespondensi satu-satu antara V(G) dg V(H) Banyaknya sisi yang menghubungkan dua titik di V(G) sama dengan banyaknya sisi yang menghubungkan dua titik di V(H) yang berkorespondensi dengan titik-titik u dan v =

8. DEFINISI Jalan (walk) adalah sebuah barisan berhingga (tak kosong) w = v 0 e 1 v 1 e 2 v 2 ….e k v k yang suku-sukunya bergantian titik dan sisi v i-1 dan v i adalah titik-titik ujung sisi e i untuk 1≤i≤k. Jejak (trail) adalah jalan yang semua sisinya berbeda. Lintasan (Path) adalah jejak yang semua titiknya berbeda. Sirkit adalah jejak tutup. Sirkit Euler adalah sirkit yang memuat semua sisi di G. Graph Euler adalah sebuah graph yang memuat sirkit euler.

9. DEFINISI Sikel (cycle) adalah sebuah jejak tertutup yang titik awal dan semua titik internalnya berbeda. Sikel Hamilton adalah sikel yang memuat semua titik dalam sebuah graph. Graph Hamilton adalah graph yang memuat sikel hamilton.

10. Contoh Graph G: • • • • • • v 1 v 3 v 4 v 5 v 6 v 2 e 6 e e e 5 e 4 e 3 e 2 e 1 e 7 e 8

11. DEFINISI G graph terhubung jhj untuk setiap dua titik di G ada lintasan di G yang menghubungkan kedua titik tersebut. Graph bagian terhubung maksimal adalah tidak ada graph bagian terhubung lain yang memuat graph bagian tersebut. Komponen dari graph G adalah sebuah graph bagian terhubung maksimal (titik dan sisi) dari G Pohon ( tree ) adalah graph terhubung yang tidak memiliki sikel. Hutan ( forest ) adalah graph yang setiap komponennya adalah pohon. Komplemen graph G ( G ) adalah graph sederhana yang himpunan titiknya sama dengan himpunan titik G, dan dua titik u dan v di G berhubungan langsung jhj di G titik u dan v tidak berhubungan langsung.

12. TEOREMA Jika G isomorfik dengan G maka |V(G)|=0(mod 4) atau |V(G)|=1(mod 4)

13. DERAJAT TITIK Definisi: Derajat titik v dilambangkan dengan d(v) adalah banyaknya sisi G yang terkait di titik v ( loop dihitung dua kali). derajat minimum: (G) = minimum {d(v); v V(G)} derajat maksimum: (G) = maksimum {d(v); v V(G)} Graph G disebut beraturan k apabila setiap titik di G berderajat k