Makalah ini membahas tentang pita energi dalam zat padat dengan 3 poin utama: 1. Menjelaskan asal mula dan besar celah energi dalam model elektron hampir bebas 2. Menguraikan fungsi Bloch dan model Kronig-Penny dalam memahami elektron dalam potensial periodik 3. Membahas jumlah orbital dalam sebuah pita energi untuk logam dan isolator

1. PITA ENERGI
Disusun untuk memenuhi tugas semester 8 dari dosen mata kuliah Pendahuluan
Zat Padat
Disusun Oleh :
Kelompok : 5
Nama : 1. Rina Dwi Aruprihartini Mulyaningsih (3215086789)
2. Fitria Herliana (3215086787)
3. Silvia Rahmawati (3215086786)
4. Agnes Novita Sari (3215086811)
5. Giri Puspita (3215086778)
Program Studi : Pendidikan Fisika Non Reguler’08
PROGRAM STUDI PENDIDIKAN FISIKA
FAKULTAS MATEMATIKA & ILMU PENGETAHUAN ALAM
UNIVERSITAS NEGERI JAKARTA
2012

2. KATA PENGANTAR
Assalaamu’alaikum warahmatullahi wabarakaatuh,
Pertama-tama kami panjatkan puji dan syukur ke hadirat Allah SWT,
karena dengan rahmat, taufik, dan hidayah-Nyalah saya dapat menyelesaikan
makalah Pendahuluan Fisika Zat Padat yang berjudul Pita Energi ini.
Adapun tujuan kami menyusun makalah ini adalah untuk memenuhi tugas
dari dosen mata kuliah Pendahuluan Fisika Zat Padat serta untuk menambah
pengetahuan kami tentang pita energi.
Dalam menulis makalah ini, tidak lupa kami sampaikan ucapan
terimakasih kepada kedua orang tua dan keluarga atas segala do’a serta
motivasinya, Bapak Dr. Erfan Handoko, M.Si selaku dosen mata kuliah
Pendahuluan Fisika Zat Padat yang telah berkenan memberikan tugas ini kepada
kami.
Kami menyadari bahwa makalah ini masih jauh dari sempurna. Oleh
karena itu, kami mengharapkan kritik dan saran demi perbaikan di masa yang
akan datang.
Wassalaamu’alaikum warahmatullahi wabarakaatuh
Jakarta, 24 Mei 2012
Penyusun

3. BAB I
PENDAHULUAN
1.1 Latar Belakang
Model elektron bebas dapat memberikan penjelasan yang baik terhadap
kapasitas panas, hantaran listrik dan kalor, kelemahan magnet dan
elektrodinamika logam Namun model ini tidak bisa memberikan penjelasan
terhadap berbagai masalah seperti:
1. Perbedaan di antara logam-logam, semi-logam, semi-konduktor dan
isolator
2. Terjadinya harga koefisien Hall yang positif
3. Hubungan antara elektron konduksi dalam logam terhadap elektron valensi
atom-atom bebas
4. Banyak sifat-sifat transport terutama mengenai magneto transport
Daya hantar listrik superkonduktor saat 1 K, < 10-10 Ω-cm sedangkan daya
hantar listrik dari isolator yang baik adalah > 1022 Ω-cm. Sifat tahanan listrik ini
dipengaruhi oleh suhu.
Untuk dapat menerangkan sifat daya hantar listrik zat padat diperlukan
sebuah model. Model yang dikembangkan adalah model elektron hampir bebas
dan teori pita energi.
1.2 Tujuan Penulisan
1. Memenuhi tugas mata kuliah pendahuluan fisika zat padat
2. Mempelajari teori pita energi
3. Mempelajari asal mula serta besar dari celah energi
4. Mempelajari fungsi Bloch dan model Kronigg-Penny
5. Mempelajari fungsi gelombang elektron dalam potesial periodik
6. Mempelajari jumlah orbital di dalam sebuah pita

4. 1.3 Sistematika Penulisan
BAB I PENDAHULUAN
1.1 Latar Belakang
1.2 Tujuan
1.3 Sistematika Penulisan
BAB II PEMBAHASAN
A. Model Elektron Hampir Bebas
1. Asal Mula Celah Energi
2. Besar dari Celah Energi
B. Fungsi Bloch
C. Model Kronig-Penny
D. Fungsi Gelombang Elektron dalam Potensial Periodik
1. Pernyataan Ulang Teorema Bloch
2. Momentum Kristal Sebuah Elektron
3. Solusi dari Persamaan Pusat
4. Model Kronig-Penny Dalam Ruang Kisi Balik
5. Pendekatan Kisi Kosong
6. Solusi Pendekatan Dekat Zona Batas
E. Jumlah Orbital dalam Sebuah Pita
1. Logam dan Isolator
BAB III PENUTUP
3.1 Kesimpulan

5. BAB II
KAJIAN TEORI
A. Model elektron Hampir Bebas
Dari bab 6 telah diketahui bahwa persamaan distribusi energi model
elektron bebas adalah:
Dimana kondisi batas pada kubus dengan sisi L adalah:
Fungsi gelombang elektron bebas
........ 1
........ 2
........ 3
Teori elektron bebas memiliki kegagalan dalam menjelaskan perbedaan
antara konduktor, semikonduktor dan isolator. Oleh karena itu, agar kita dapat
memahami perbedaan tersebut, kita menggunakan teori yang mirip dengan teori
elektron bebas tetapi sedikit dimodifikasi, yaitu model elektron hampir bebas.
Gambar 1 kurva a. Energi sebagai fungsi vektor gelombang k menurut model
elektron bebas.

6. Gambar 2 kurva b. Kurva energi (E) sebagai fungsi vektor gelombang (k)
dalam sebuah kristal monoatomik satu dimensi dengan konstanta kristal
sebesar a. Celah energi Eg yang ditunjukkan terjadi pada k = ± p/a. Celah
energi lainnya ditemukan pada ± np/a, untuk nilai integral dari n.
syarat terjadinya difraksi Bragg adalah ( k + G )2 = k2.
Dalam satu dimensi, persamaan tersebut menjadi:
........ 4
dimana G = 2nπ/a adalah vektor kisi resiprok dan n adalah bilangan bulat. Celah
energi pertama terjadi untuk nilai k = + π/a. Ingat bahwa daerah antara - π/a
dengan + π/a disebut daerah Brillouin pertama. Celah energi-celah energi yang
lainnya terjadi untuk nilai-nilai k yang merupakan kelipatan dari + π/a.
Fungsi gelombang di titik k = + π/a merupakan fungsi gelombang hasil
interferensi antara gelombang yang berjalan ke kanan dan ke kiri. Hal ini dapat
terjadi jika syarat difraksi Bragg terpenuhi oleh fungsi gelombang k. Hasilnya,
fungsi gelombang di titik k = + π/a merupakan gelombang berdiri.
Fungsi gelombang berdiri tersebut terdiri atas dua macam, yaitu fungsi
gelombang yang saling menguatkan dan fungsi gelombang yang saling
melemahkan. Secara matematik, kedua fungsi gelombang berdiri tersebut dapat
dibentuk dari fungsi gelombang yang berjalan ke kanan dan ke kiri, yaitu sebagai
berikut:

7. 1. Asal Celah Energi
........ 5
Asal mula adanya celah energi yaitu kedua fungsi gelombang φ (+) dan φ
(-) (seperti persamaan 5) menumpukkan elektron di dua tempat yang berbeda,
dan karena itu, kedua kelompok elektron itu memiliki nilai energi potensial yang
berbeda.
Kerapatan muatan pada kedua gelombang berdiri tersebut adalah:
Persamaan di atas akan menumpukkan elektron di atas ion-ion positif yang
dipusatkan di titik-titik x = 0, + a, + 2a, + 3a, dst. Lihat gambar 3, kelompok
elektron ini berada di daerah yang berenergi potensial rendah.
Persamaan di atas akan menumpukkan elektron-elektron tersebut di tengah-tengah
antara ion-ion positif tersebut, sehingga elektron-elektron ini memiliki energi
potensial yang tinggi.

8. Gambar 3
Fungsi gelombang di titik A tepat di bawah celah energi pada gambar 2 di
atas adalah φ (+) sedangkan di titik B tepat di atas celah energi adalah φ (-).
2. Besar Celah Energi
Fungsi gelombang pada batas zona Brillouin k = π/a adalah
dan yang dinormalisasikan.
Kita misalkan energi potensial sebuah elektron di titik x dalam kristal itu sebagai:
Maka kita dapat menentukan nilai energi celah, Eg (yaitu perbedaan energi antara
kedua gelombang berdiri) sebagai berikut:
........ 6

9. Jadi, nilai energi celah ini sama dengan komponen dari deret Fourier energi
potensial.
B. Fungsi Bloch
Fungsi Bloch membuktikan perlunya teorema bahwa solusi dari
persamaan Schrodinger untuk potensial periodik harus dalam bentuk khusus.
= periode kisi kristal
Teorema Bloch:
Fungsi eigen dari persamaan gelombang untuk suatu potensial periodik adalah
hasil kali antara suatu gelombang bidang dengan suatu fungsi
dengan periode sifat kisi kristal.
Fungsi Bloch berlaku ketikatidak berdegenerasi, yaitu ketika tidak ada fungsi
gelombang lain dengan energi sama dan vektor gelombang sebagai .
N = kisi kristal pada lingkaran Na
Energi potensial dalam a, dimana U (x) = U (x + sa), dimana s adalah bilangan
bulat. Maka solusi dari fungsi gelombang adalah:
Dimana C adalah konstan, maka kejadian di sekitar lingkaran Na adalah:
karena harus bernilai tunggal.
........ 7
........ 8

10. Maka kita dapat melihat bahwa:
Dimana:
C. Model Kronig-Penney
........ 9
........ 10
Potensial periodik yang merupakan persamaan gelombang dapat
diselesaikan dalam fungsi dasar seperti pada gambar 4. Persamaan gelombangnya
adalah:
Dimana:
U(x) = energi potensial
........ 11
= nilai eigen energi
Model ini menjelaskan tingkah laku elektron dalam sebuah energi
potensial yang periodik, dengan menganggap energi potensial periodik itu
merupakan deretan sumur energi potensial persegi seperti ditunjukkan dalam
gambar 4 di bawah ini.

11. Gambar 4 Energi potensial periodik satu dimensi yang digunakan oleh Kronig
dan Penney.
Di dasar sumur, yaitu untuk 0 < x < a, elektron dianggap berada di sekitar
sebuah inti atom (atau diantara dua inti atom), dan energi potensialnya dianggap
nol, sehingga di daerah ini elektron bertingkah sebagai elektron bebas.
Sebaliknya, di luar sumur, yaitu untuk –b < x < 0, energi potensial elektron
dianggap sama dengan U0.
Fungsi-fungsi gelombang elektron diperoleh dari persamaan Schrodinger
untuk kedua daerah (yaitu daerah 0 < x < a, dan daerah –b < x < 0) sebagai
berikut:
Wilayah 0 < x < a saat U = 0, eigenfunction adalah kombinasi linear
Bidang gelombang berjalan ke kanan dan ke kiri, dengan energi:
Dalam daerah –b < x < 0 solusi penghalangnya berbentuk
Dengan
Solusi dari persamaan (7) pada wilayah a < x < a + b harus dikaitkan
dengan solusi persamaan (14) pada wilayah –b < x < 0 dengan teorema Bloch:
Konstanta A, B,C, D dipilih sehingga dan kontinu pada x = 0 dan x = a.
Saat x = 0
A + B = C + D
iK(A – B) = Q(C – D)
........ 12
........ 13
........ 14
........ 15
........ 16
........ 17
........ 18

12. Saat x = a
Dengan menggunakan persamaan 16, didapat:
Keempat persamaan linier yang homogen ini (Persamaan 17 sampai 20)
akan memiliki solusi jika determinan dari koefisien-koefisien A, B, C, dan D
adalah sama dengan nol. Atau jika
Hasilnya akan menjadi sederhana, ketika batasnya b = 0 dan U = ~
menjadi Q2ba/2 = P. Dalam batas ini Q > K dan Qb < 1. Kemudian 21a mereduksi
menjadi:
(P/Ka) sin Ka + cos Ka = cos ka
Gambar 5
........ 19
........ 20
........ 21 a
........ 21 b

13. D. Fungsi Gelombang Eletron Dalam Potensial Periodik
Deret Fourier untuk energi potensial:
Fungsi nyata dari UG adalah:
Secara eksplisit, persamaan gelombang adalah:
Fungsi gelombang ψ(x) dapat dinyatakan sebagai deret Fourier
........ 22
........ 23
........ 24
........ 25
Dimana
k = bilangan real (k = 2πn/L)
n = bilangan bulat
Untuk menyelesaikan persamaan gelombang, kita subtitusikan persamaan 25 ke
dalam 24.
Energi Kinetik

14. Energi Potensial
Persamaan gelombang merupakan jumlah dari energi kinetik dan energi potensial:
Setiap komponen Fourier harus memiliki koefisien yang sama pada kedua sisi
persamaan ini
Dengan notasi
1. Pernyataan Ulang Teorema Bloch
Bila kita menentukan C pada persamaan 27, persamaan gelombang pada
persamaan 25 menjadi:
Menurut aturan
Dengan
Karena uk (x) adalah deret Fourier vektor kisi resiprok dan T adalah
translasi kisi kristal, maka uk (x) = uk (x + T). Maka:
........ 26
........ 27
........ 28
........ 29

15. Karena exp (-iGT) = 1, maka uk (x + T) = uk (x). Ini merupakan bukti dari
teorema bloch yang berlaku bahkan saat ψk berdegenerasi.
2. Momentum Kristal Sebuah Elektron
Arti penting dari k vektor gelombang digunakan untuk label fungsi Bloch:
 Dalam translasi kisi kristal yang membawa r pada r + T, kita mempunyai
........ 30
Karena uk (r + T) = uk (r) dengan demikian exp (ik.T) adalah faktor fase
dimana fungsi Bloch dikalikan ketika kita membuat translasi kisi kristal.
 Jika potensi kisi hilang, persamaan pusat mengurangi ke (λk – ε)C(k) = 0,
sehingga semua C (k - G) adalah nol kecuali C (k), dan dengan demikian
uk (r) adalah konstan. Kami memiliki ψk(r) = ℯikr , seperti untuk elektron
bebas.
 k masuk dalam hukum yang mengatur peristiwa tabrakan dalam kristal.
3. Solusi dari Persamaan Pusat
Persamaan 27 disebut persamaan pusat
........ 31
Persamaan tersebut merupakan satu set persamaan linear yang
menghubungkan koefisien C(k – G) untuk semua vektor resiprok G. Persamaan
ini akan konsisten jika determinan dari koefisien sama dengan 0.
Kita asumsikan bahwa energi potensial U (x) hanya mengandung satu komponen
Fourier Ug = U-g yang dinotasikan oleh U. Koefisien determinannya:
........ 32

16. Dengan k yang diberikan, setiap akar E atau Ek terletak di sebuah pita
energi yang berbeda, kecuali dalam kasus kebetulan.
4. Model Kronig-Penny Dalam Ruang Kisi Balik
Persamaan 31 diselesaikan dengan model Kronig Penney pada delta
periodik-fungsi potensial.
Dimana A adalah konstan dan a adalah kisi spasi. Jumlah yang lebih dari semua
bilangan buat s antara 0 dan 1/a. Syarat batas berkala atas cicin satuan panjang,
yang berarti lebih dari 1/a atom. Dengan demikian koefisien fourier potensial
adalah:
Kami tulis persamaannya dengan k sebagai indeks Bloch, ini menjadi:
Di mana dan jumlah yang lebih dari semua bilangan bulat n, kita
ingin memecahkan persamaan diatas untuk kita mendefinisikan
Maka persamaannya menjadi
........ 33
........ 34
........ 35
........ 36

17. ........ 37
Karena jumlah persamaan 36 adalah semua koefisien C, kita memiliki untuk
setiap n yaitu:
Hubungan ini dapat dituliskan
........ 38
........ 39
Jumlah kedua belah pihak untuk mendapatkan semua n, menggunakan persamaan
36 dan menghilangkan f(k) dari kedua belah pihak
penjumlahan dapat dihitung dengan bantuan hubungan standar
........ 40
........ 41
setelah manipulasi trigonometri di mana kita menggunakan hubungan untuk
selisih dua cotangents dan produk dari dua sinus, jumlah pada persamaan (40)
menjadi
Dimana
Hasil dari persamaan (40) adalah
........ 42
........ 43
yang sesuai dengan hasil Kronig-Penney (21b) dengan P ditulis untuk .
5. Pendekatan Kisi Kosong
Struktur pita yang sebenarnya biasanya dipamerkan sebagai bidang energi
berlawanan dengan vektor gelombang di zona Brilouin pertama. Ketika vektor

18. gelombang diberikan di luar zona pertama, mereka dibawa kembali ke dalam zona
pertama dengan mengurangi vektor kisi cocok timbal balik.
Ketika energi pita yang diperkirakan cukup baik dengan energi elektron
bebas , disarankan untuk memulai perhitungan dengan melakukan
energi elektron bebas kembali ke dalam zona pertama. Prosedur ini cukup
sederhana sekali Anda dapat menguasainya. Cari nilai G sehingga k’ di zona
pertama dapat ditentukan.
di mana k tidak terbatas dan merupakan vektor gelombang elektron bebas dalam
kisi kosong.
Jika kita menjatuhkan K sebagai bagasi yang tidak perlu, energi elektron bebas
selalu dapat ditulis sebagai
Dengan K di zona pertama dan G diizinkan untuk menjalankan lebih dari titik-titik
kisi timbal balik. Misalkan, kita ingin menunjukkan energi sebagai fungsi
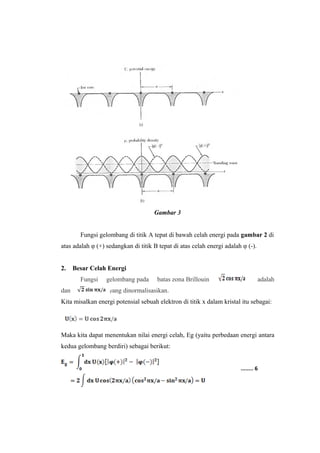
dari K dalam bidang arah [100] . Untuk, pilih unit tersebut bahwa . Kami
menunjukkan beberapa dataran rendah di pita ini pendekatan kisi kosong dengan
energi mereka di k = 0 dan panjang sumbu kx di zona pertama.
Pita-pita elektron bebas diplot pada Gambar 8.

19. Gambar 8
Perkiraan solusi Dekat Batas Zona
Vektor gelombang pada batas zona 1/2G, yaitu pada m/a.
sehingga pada batas zona energi kinetik dari dua komponen gelombang K= ±1/2G
adalah sama.
Jika C (1/2G) adalah koefisien penting dalam 29 orbital pada batas zona, daripada
C (-1/2G) juga merupakan koefisien penting. Hasil ini juga mengikuti dari
disscussion dari 5. Kami retaint hanya persamaan dalam persamaan pusat yang
mengandung kedua koefisien C (1/2G) dan C (-1/2G), dan mengabaikan semua
koefisien lainnya.
Satu persamaan 31 menjadi, dengan K = 1/2G dan
persamaan dari 31 menjadi
........ 44
........ 45
Ini dua persamaan memiliki solusi trivial untuk koefisien benar jika e energi
memenuhi
........ 46

20. ketika
........ 47
Energi ini memiliki dua akar, satu lebih rendah dari energi kinetik elektron
bebas oleh U, dan satu yang lebih tinggi dengan U. Jadi energi potensial 2 U cos
Gx telah menciptakan sebuah energi gap 2U pada batas zona. Rasio C mungkin
dari 44 atau 45:
........ 48
langkah terakhir menggunakan persamaan 47. Jadi ekspansi Fourier pada
batas zona memiliki solusi dua.
Kami menggunakan pendekatan yang sama untuk komponen, sekarang dengan
fungsi gelombang dari formulir.
Sebagaimana diarahkan oleh persamaan 31:
........ 49
dengan λk didefinisikan sebagai . persamaan ini memiliki solusi jika
energi satis sebuah
Ketika
Energi ini memiliki dua akar:
........ 50
Dan setiap akar menggambarkan sebuah pita energi, diplot pada gambar 9. Hal ini
........ 51

21. mudah memperluas energi, dalam hal K kuantitas (tanda atas K disebut tilde),
yang mengukur perbedaan wavevector antara K dan batas zona.
Di wilayah . Berikut seperti sebelumnya.
Gambar 9
dua akar batas zona 47 sebagai kita dapat menulis persamaan 51 sebagai:

22. ........ 52
Ini adalah akar untuk energi ketika wavevector sangat dekat dengan batas zona di
1/2G.
E. Jumlah Orbital Dalam Sebuah Pita
Mempertimbangkan kristal dibentuk dari bilangan genap N dan kisi
konstan. Nilai-nilai yang diperbolehkan dari gelombang elektron vektor k di zona
Brilouin pertama adalah:
........ 53
Kami memotong rangkaian di Nπ/L=π/a, ini adalah batas zona.
Titik -Nπ/L=-π/a tidak akan dihitung sebagai titik independen karena terhubung
dengan vektor kisi timbal balik dengan π/a,yaitu jumlah total sel N.
Setiap sel berkontribusi hanya satu nilai independen k untuk setiap kisi
energi. Hasil ini membawa lebih ke dalam tiga dimensi. dengan pertimbangandua
orientasi independen dari spin elektron, ada 2N orbital independen dalam
setiap kisi energi.
Ada atom tunggal valensi satu di setiap sel, kisi ini dapat setengah diisi
dengan elektron. Jika setiap atom memberikan kontribusi dua
elektron valensi untuk kisi, kisi ini bisa diisi penuh. Jika ada dua atom valensi satu
di setiap sel, kisi ini juga dapat diisi penuh.
1. Logam dan Isolator
Jika elektron valensi mengisi satu atau lebih kisi dan yang lain kosong
maka disebut isolator. Medan listrik eksternal tidak akan menimbulkan aliran arus
pada isolator. Kristal dapat menjadi isolator jika jumlah elektron valensi dari
kristal adalah bilangan bulat.
Logam-logam alkali dan logam-logam mulia memiliki 1 elektron valensi
per sel, sehingga mereka disebut logam. Logam alkali tanah memiliki 2 elektron

23. valensi, mereka bidsa menjadi isolator. Berlian, Silikon dan Germanium masing-masing
memiliki 2 atom valensi 4, sehingga ada 8 elektron valensi per sel.
BAB III
PENUTUP
A. Kesimpulan
1. Solusi dari persamaan gelombang dalam kisi kristal dari Bloch
dimana uk (r) adalah sama dalam translasi kisi kristal.
,
2. Ada daerah energi yang bukan solusi dari fungsi Bloch. Energi ini
membentuk daerah terlarang dimana fungsi gelombang yang teredam
dalam ruang-ruang dan nilai-nilai k yang kompleks, seperti pada gambar
di bawah ini.

24. Adanya daerah energi terlarang merupakan syarat terjadinya isolator
3. Pita energi dapat didekati dengan satu atau dua bidang gelombang, contoh
4. Jumlah orbital dalam pita adalah 2N, dimana N adalah jumlah sel dalam
specimen
B. Saran
Kami menyadari bahwa makalah ini masih jauh dari sempurna. Oleh
karena itu, kami mengharapkan kritik dan saran demi perbaikan di masa yang
akan datang.
DAFTAR PUSTAKA
1. Charle Kittel, Introduction to Solid State Physics, sixth ed., John Wiley &
Sons, Inc., New York, 1996.
dekat dengan daerah batas